
Сейчас в различных источниках имеется огромное количество статей, материалов конференций, телеграм-каналов и открытых репозиториев в GitHub на любую тему из сферы Data Science. В статье хочется обратить ваше внимание на отдельный класс задач, которому, по нашему мнению, уделяют меньше внимания и который не так часто встречается в рамках Data Science кейсов, соревнований или хакатонов.
Речь пойдет о «Других» рекомендациях — ML-системах, которые уже нельзя отнести к рекомендательным в популярном/классическим смысле. Давайте разберемся, что для нас классика, а что — нет.
Классические рекомендации.
На какой вопрос необходимо ответить:
Как порекомендовать определенному пользователю музыкальный плейлист, который ему понравится?
Какой товар порекомендовать пользователю в интернет-магазине?
У нас есть: большая матрица user-item.
Мы делаем:
Например, матричное разложение.
Формируем предложение на основе интереса похожих пользователей.
«Другие» рекомендации.
На какой вопрос необходимо ответить:
Сколько нужно добавить материалов (например, ферросплавов), чтобы сталь получилась с нужной «химией»?
Какое значение управляющего параметра выставить, чтобы избежать дефекта на производстве?
У нас есть: исторические данные с информацией о целевой переменной и режимах работы оборудования на производстве.
Мы делаем:
Модель симуляции процесса — прогнозная модель.
Рекомендации оптимальных управляющих параметров — решаем обратную задачу оптимизации.
Почему мы используем название «Другие» рекомендации:
В сценариях, в которых используется данный подход, чаще всего модель/система используется в качестве советчика.
Если попытаться адаптировать методы «Классических рекомендаций» на «Другие рекомендации», то возникает первичный вопрос, что использовать в качестве «user» и «item», когда мы рассматриваем технологический процесс, в котором есть состояние системы, управляющие параметры и целевой таргет. Например, можно попробовать построить матрицу, где в качестве строк будут допустимые состояния системы, а в качестве столбцов — допустимые управления. Но при таком подходе к моделированию непонятны следующие моменты:
что делать, если целевых таргетов несколько, следовательно, требуется несколько моделей и при этом хочется, чтобы была возможность связывать модели друг с другом;
размерность пространства возможных состояний и управляющих параметров экспоненциально растет в зависимости от их размерности;
неясно, как явно учитывать априорное знание, что зависимость управляемых параметров и целевой переменной линейна;
и многие другие неочевидные моменты.
Свежим примером задачи в постановке «Других» рекомендаций является задача, предложенная в рамках хакатона от компании «ЕВРАЗ». В одной из задач участникам было предложено построить модели для прогнозирования содержания углерода и температуры чугуна по завершении процесса продувки металла на кислородном конвертере. Дополнительно участникам необходимо было предложить подходы, которые позволят формировать рекомендации для получения заданного уровня целевых характеристик.
Рассматриваемую постановку задачи для рекомендаций можно встретить в e-commerce при решении задачи динамического ценообразования, где роль управляемых параметров может играть стоимость товара и требуется найти такую цену, которая, например, будет максимизировать оборот по продажам товара.
Подготовленный материал разбит на две отдельные статьи: первая часть материала с описанием общей постановки задачи и возможных подходов к решению представлена ниже, а вторая, более практическая часть, будет опубликована отдельным постом. В ней я рассмотрю часть подходов на реальной Data Science, а именно — на задаче рекомендации ферросплавов из черной металлургии.
Математическая постановка задачи
Привычная оптимизация
Думаю, большей части читателей знакома общая постановка задачи математической оптимизации, которая заключается в поиске экстремума одной или нескольких функций в заданной области или без ограничений (для удобства далее рассматривается задача минимизации) и может быть записана следующим образом:
при следующих ограничениях на
где
— целевые (критериальные) функции;
,
— ограничения типа равенств на
;
,
— ограничения типа неравенств на
.
Выше приведена общая постановка задачи оптимизации, которая имеет огромное количество отдельных подклассов в зависимости от:
количества целевых функций
:
при
— многокритериальная оптимизация;
при
— однокритериальная оптимизация Кажется, что привычнее использовать «single/multi objective optimization», но в статье далее будем использовать русскоязычные аналоги.
типа ограничений
и целевых функций
:
линейные;
выпуклые;
нелинейные;
и многие другие классы.
типа координат вектора
:
непрерывные;
целочисленные;
смешанные.
размерности вектора
:
при
— многомерная оптимизация;
при
— одномерная оптимизация.
того, учитываются ли явно случайные факторы (стохастическое программирование):
критерий в форме вероятности или математического ожидания;
случайные величины в модели;
и другие варианты.
Приведенный перечень подклассов не покрывает все многообразие задач, которые могут встречаться в научной и прикладной среде, и, естественно, группировка может быть осуществлена иным образом. Это, в свою очередь, привело к тому, что существуют специализированные методы, и не один, для решения конкретного типа задачи оптимизации. Да и в целом, всегда проводятся исследования в этом направлении.
Цель данной статьи — не разобраться во всех методах для каждого отдельного случая, а рассказать о том, в каком классе задач / кейсе машинного обучения необходимо помнить о методах оптимизации, их возможностях и ограничениях, а также, какими инструментами можно пользоваться. И прежде чем пощупать оптимизацию на реальном кейсе, предлагаю глубже погрузиться в техническую сторону «Других рекомендаций».
Принцип работы системы
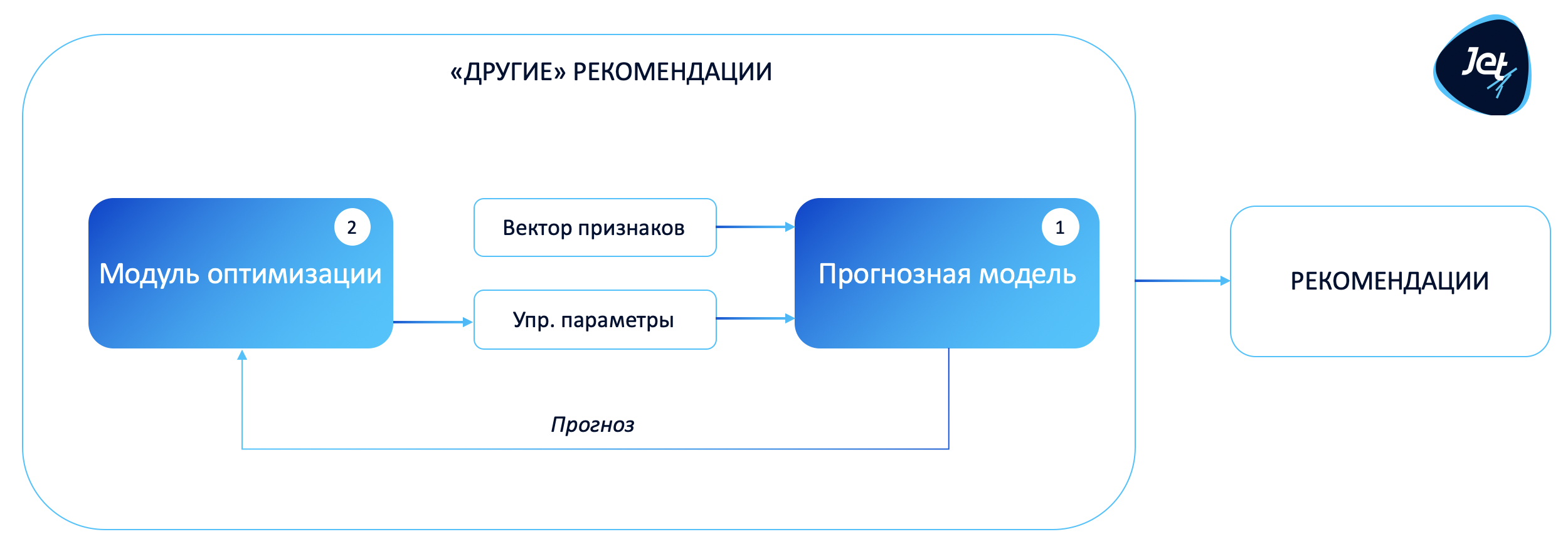
Рекомендательная система состоит из двух ключевых компонент:
Прогнозная модель (модель симуляции).
Основной задачей компоненты является получение прогноза целевого показателя при заданных управляющих параметрах. Прогнозная модель позволяет выполнять эксперименты в «виртуальном мире» и отвечать на вопрос: «А что мы получим при таком управлении?»
Заметка: здесь нет ничего нового для DS-специалиста, за исключением того, что мы должны держать в голове, что на вход модели подаются данные двух типов: фиксированные и управляющие. Управляющие параметры — это непосредственно те «рычажки», которые мы в дальнейшем хотим оптимизировать.Модуль оптимизации (решение обратной задачи).
Используя прогнозную модель, необходимо найти оптимальные управляющие параметры с учетом технологических и бизнес-ограничений. Критерий оптимальности выбора параметров управления определяется через задание целевой функции (в общем случае функция может быть не одна).
Введенные допущения
Для компактности записи будем предполагать, что разрабатываемая рекомендательная система зависит от одной прогнозной модели, но в общем случае в систему могут входить сразу несколько прогнозных моделей, использование которых может предполагаться в последовательном или параллельном режимах.
Прогнозная модель
Введем следующие обозначения:
— вектор фиксированных параметров;
— вектор управляющих параметров;
— количество наблюдений в исторических данных;
— матрица наблюдений фиксированных и управляющих параметров;
— вектор наблюдений целевой переменной.
Используя классические алгоритмы машинного обучения, такие как Ridge, Lasso, Random Forest, Gradient Boosting и др., построим отображение:
где — модель машинного обучения,
— прогноз целевой переменной при заданных фиксированных и управляющих параметрах.
Пример
Вы сталевар. Ваша задача — оптимальным путем (что считать оптимальным, определим позднее) изготовить сталь по требованиям заказчика или ГОСТа.
На вход сталевар получает чугун и/или лом, из которых мы можем составить вектор
фиксированных параметров, что в него может входить:
- химический состав чугуна;
- температура чугуна;
- историческая информация о составе лома;
- вес чугуна и лома;
- параметры агрегатов, на которых будет выполняться обработка.В процессе плавки сталевар может формировать следующие управляющие воздействи
:
- добавлять или не добавлять материалы (причем ферросплавы могут быть различного типа по содержанию ключевых элементов (например, ферросилиций (FeSi) или ферромарганец (FeMn)));
- продувать полупродукт (первичная смесь чугуна и лома) кислородом 10 или 15 минут;
- и другие возможности.Все вышеописанное необходимо для того, чтобы удовлетворить требования заказчика. Например, содержание Mn должно лежать в диапазоне от 0,5 до 0,6%, т.е. целевой переменно
является содержание Mn в стали.
Замечания:
Для формирования прогноза можно использовать известные или разработанные детерминированные формулы/правила. Например, пробовать использовать физико-химические закономерности. Не всегда целесообразно применять модели машинного обучения для описания некоторого процесса. Как один из вариантов — использовать комбинированный подход, в котором совместно используются физико-химические модели и модели машинного обучения.
В дальнейшем для решения задачи оптимизации будем разделять прогнозные модели на следующие типы:
Табличные.
Для формирования прогноза используется заранее посчитанное значение из таблицы, выбор которого зависит от фиксированных и управляющих параметров.Доступен явный вид модели.
Например, для линейных моделей нам известен явный вид, т.е. возможно на листочке выписать аналитический вид модели, что позволяет воспользоваться богатым инструментарием математического анализа и не только.Недоступен явный вид модели.
Например, для популярного градиентного бустинга нет возможности получить явную зависимость, т.е. в данном случае модель является некоторым «черным ящиком». Сейчас популярны и активно развиваются математические подходы для объяснения принципа работы моделей, не имеющих явного вида:SHAP — Python библиотека, под «капотом» которой используются принципы из теории игры;
Lime — Python библиотека, базирующаяся на локальной линейной аппроксимации;
Monoforest — подход, использующий разложение ансамбля деревьев в полином относительно индикаторных функций. Далее из полученного представления оценивается важность каждого индикатора и «сила» признаков.
Замечание: перечисленные выше подходы все равно не дают явного вида зависимости, а лишь рассчитывают оценки локальной (для фиксированной точки) и глобальной (для модели) важности признака.
Модуль оптимизации
Запишем задачу оптимизации с учетом прогнозной модели и обозначений, введенных выше:
и определяется следующими ограничениями
где
— заданные фиксированные параметры (знак * добавлен для того, чтобы подчеркнуть, что выбрана некоторая точка);
— целевая функция (функция ошибки)
;
— область допустимых значений управляющих параметров;
— ограничения типа равенств
;
— ограничения типа неравенств
.
Пример
Продолжим рассматривать пример из черной металлургии.
Для формализации понятия оптимальности необходимо определить целевую функцию
, которая бы оптимизировала процесс. Один из вариантов — снизить себестоимость продукции за счет более экономичного использования ферросплавов:
где — вектор стоимостей ферросплавов и
— вектор ферросплавов (управляющих параметров).
Без ограничений на
задача имеет тривиальное решение на минус бесконечности, которое, конечно же, невозможно применить в реальной жизни.
Первая категория ограничений на
.
Любой материал может в момент формирования рекомендации отсутствовать или быть в очень ограниченном количестве, поэтому необходимы ограничения типа неравенств.
Вторая категория ограничений на
.
При изготовлении стали у сталевара есть диапазоны по химическому составу, которые определяются маркой стали, и в них обязательно надо попасть. Теперь вспомним, что наша целевая переменная как раз определяет содержание химического элемента в стали. Следовательно, нам необходимо ввести ограничения типа неравенствна прогноз модели.
Выбор конкретного метода оптимизации для решения сформулированной задачи напрямую зависит от типа целевой функции, управляющих параметров, ограничений, доступных вычислительных ресурсов и требований к быстродействию. Далее немного подробнее рассмотрим часть подходов к решению, используемых методов и библиотек.
Подходы к решению обратной задачи
Однокритериальная оптимизация
Перебор по сетке
Описание
Надо с чего-то начать и, наверное, лучше всего стартовать с простого и детерминированного baseline-подхода. На области , пространстве всевозможных значений управляющих параметров, определим набор точек с некоторым шагом, т.е. зададим сетку, в которой выполняется расчет целевой функции, а затем выбирается точка с наилучшим значением целевой функции. Если размерность сетки (количество точек) перебора слишком велика для ваших вычислительных ресурсов, то точки для выполнения расчета можно выбирать случайно.
Данный подход аналогичен привычным для DS-специалистов методам из scikit-learn GridSearchCV и RandomizedSearchCV, используемых для подбора гиперпараметров прогнозной модели.
Плюсы
простой алгоритм;
простота анализа результатов;
универсален (не зависит от типа прогнозной модели);
если все управляющие параметры — дискретные, то полный перебор по сетке обеспечит нахождение глобального оптимума.
Минусы
чаще всего для получения качественного решения требуется большое количество точек
долгое время расчета;
время вычисления растет экспоненциально в зависимости от количества управляющих параметров;
не всегда очевидно, каким образом сформировать сетку;
чаще качество решения хуже, чем у других подходов (за исключением случаев, где возможен полный перебор допустимых значений);
отсутствует возможность явно учесть дополнительные (линейные и нелинейные) ограничения на управляющие параметры. Для учета можно пробовать:
либо проверять по фактическому удовлетворению ограничениям;
либо формировать более сложную процедуру генерации допустимых управляющих параметров, например, методом Hit-and-Run, который позволяет генерировать точки в некотором выпуклом множестве.
Рассмотрим модельно-прикладной пример
Перед вами стоит задача поддерживать заданную температуру внутри некоторого помещения. В качестве управляющего воздействия можно включать/выключать (1/0) источник тепла. Допустим, мы имеем возможность в каждый дискретный момент времени формировать управляющее воздействие. В данном случае управляющее воздействие принимает всего два состояния, поэтому проще промоделировать, что будет на шаге
при каждом возможном значении управляющего параметра, и выбрать лучший вариант.
Для базовых рекомендаций лучше метода не придумаешь: просто, быстро и понятно.
Байесовская оптимизация
Описание
Математика, которая стоит за байесовской оптимизацией (далее — БО) — это вопрос отдельной работы. Ключевым для нас является тот факт, что БО — это некоторое улучшение случайного перебора по сетке, который пытается выделить область внутри нее, где вероятность получить экстремальное значение выше и, соответственно, можно чаще генерировать точки в этих областях для поиска решения.
HyperOpt, Optuna и BayesianOptimization — популярные Python библиотеки, использующие данный подход. И это, естественно, не полный список. Чаще всего сейчас перечисленные библиотеки используются для подбора гиперпараметров прогнозных моделей, но мощь данных инструментов можно использовать и для задачи, поставленной в разделе Модуль оптимизации.
Плюсы
универсален (не зависит от типа прогнозной модели);
удобный интерфейс библиотек HyperOpt, Optuna и BayesianOptimization (естественно, каждый из них где-то удобнее, мой фаворит — Optuna);
хорошая документация библиотек HyperOpt, Optuna и BayesianOptimization;
в Optuna имеются удобные инструменты для визуализации процесса оптимизации;
в среднем качество и скорость решения выше, чем от простого перебора по сетке;
возможность задания смешанной сетки (непрерывные и дискретные переменные);
возможность задания априорного распределения на параметры сетки.
Минусы
нетривиальная математика «под капотом» (если пробовать разобраться, то придется вспомнить Гауссовские процессы и не только);
отсутствует возможность явно учесть дополнительные (линейные и нелинейные) ограничения на управляющие параметры.
Замечание
Ключевым минусом использования БО для поиска оптимальных управляющих параметров является невозможность явного учета дополнительных ограничений на управляющие параметры или прогноз модели.
Для того, чтобы учесть ограничения, можно воспользоваться аналогичным подходом, как и в методе внутренней точки, который используется в выпуклой оптимизации. То есть исходную задачу условной оптимизации из раздела Модуль оптимизации свести к следующей задаче безусловной оптимизации (запишем для случая однокритериальной оптимизации).
где и
— коэффициенты для учета важности, масштаба и/или размерности ограничения в целевой функции. Конечно, нужно помнить про условия оптимальности Каруша — Куна — Таккера для задачи условной оптимизации, но при использовании прогнозной модели в качестве
данные условия проверить достаточно проблематично.
Специальные классы задач
Теперь предлагаю обсудить частные случаи, для которых имеется как теоретическая (теоремы о существовании решения, скорости сходимости и др.), так и практическая база (специализированные алгоритмы решения, численные методы и типовые прикладные постановки задач). Рассмотрим следующие типы задач:
задача линейного программирования (далее — ЛП);
задача смешанного целочисленного линейного программирования (далее — СЦЛП).
При описании постановки задачи оптимизации в разделе Модуль оптимизации особое внимание стоит уделить тому, что в целевой функции и ограничениях есть зависимость от прогнозной модели, описанной в разделе Прогнозная модель. Поэтому для того, чтобы сформулировать задачу в терминах ЛП и СЦЛП, прогнозная модель должна быть из класса линейных моделей и ограничения должны быть линейными.
Пример
Продолжим рассматривать пример из черной металлургии. Уточним ограничения на задачу, если в качестве прогнозной модели используем линейные алгоритмы.
и определяется следующими ограничениями:
где и
— векторы коэффициентов линейной модели, соответствующие фиксированным и управляющим параметрам,
— сдвиг линейной модели. Получили в чистом виде задачу линейного программирования.
ЛП
Задача ЛП является достаточно хорошо изученной и имеет большое количество реализаций на различных языках программирования. Для реализации на языке Python можно использовать метод linprog из популярной библиотеки Scipy и библиотеку Pulp.
Плюсы
хорошо изученная задача;
явная поддержка дополнительных линейных ограничений;
в отдельных случаях найденное решение будет оптимальным;
удобный интерфейс в Scipy;
детальная документация в Scipy;
быстрое время работы (с поправкой на размерность задачи).
Минусы
при переносе задачи с листочка в код не всегда «приятно» составлять матрицу
и вектор
ограничений (здесь легко ошибиться);
нет возможности учесть нелинейные ограничения и, как следствие, в качестве прогнозной модели нельзя использовать нелинейные модели.
СЦЛП
Задача СЦЛП является более сложной и реже встречающейся относительно задачи ЛП. Не так много библиотек на языке Python поддерживают целочисленные переменные. Мы используем достаточно популярную библиотеку Pulp, которая славится своей высокой производительностью, поддержкой современных методов решений и специфичным интерфейсом.
Данный алгоритм полезно использовать, когда один или несколько управляющих параметров являются категориальными. Например, управляющий параметр задает режим продувки металла на агрегате, который имеет четыре допустимых значения.
Плюсы
специализированные методы для обработки целочисленных переменных;
явная поддержка дополнительных линейных ограничений;
для отдельных случаев — нахождение оптимального решения;
быстрое время работы (с поправкой на размерность задачи);
поддержка бесплатных методов решений;
поддержка продвинутых платных методов решений (например, CPLEX и GUROBI).
Минусы
непрозрачная документация;
не самый удобный интерфейс;
нет возможности учесть нелинейные ограничения и, как следствие, в качестве прогнозной модели нельзя использовать нелинейные модели.
Нелинейная оптимизация из коробки
Задача нелинейной оптимизации совсем нетривиальна и имеет много подводных камней. Да, имеется огромное количество методов, которые разработаны для решения данной задачи, но каждый из них имеет ряд ограничений на применимость. Стоит отметить, что подготовка всех требуемых параметров (градиент, гессиан, начальная точка и др.) для метода является наиболее важным шагом, так как допущенная на данном этапе ошибка может привести к тому, что применяемые методы будут «расходиться».
Ниже — перечень библиотек, которыми можно воспользоваться:
scipy, но больший интерес представляет метод
scipy.optimize.minimize, внутри которого реализованы различные методы для условной и безусловной оптимизации;pyomo — реализованы алгоритмы для линейной, квадратичной, нелинейной и целочисленной оптимизации;
PyGad Python библиотека с реализованными генетическими алгоритмами.
Плюсы
универсальны (не зависят от типа прогнозной модели);
возможна поддержка линейных и нелинейных ограничений;
удобные интерфейсы;
хорошая документация.
Минусы
тонкая настройка входных параметров;
трудно удовлетворить всем требованиям некоторого метода;
большая вариативность методов (везде свои требования к входным данным: градиент, гессиан; различные подходы для оценки, например, градиентов);
требуется глубокое погружение в алгоритм при использовании.
Замечание
В своей практике мы активно используем метод scipy.minimize(method=’trust-constr’), который базируется на определении области вокруг оптимального решения и квадратичной аппроксимации целевой функции. Подробнее можно почитать здесь.
Многокритериальная оптимизация
Задача очень непростая и, кажется, во многих случаях оптимального управления, удовлетворяющего ограничениям и нескольким критериям, не существует. Но все же подходы и методы решения существуют, хотя для их понимания требуются подготовка и терпение.
Пример
И снова черная металлургия, но задача другая.
На одном из этапов изготовления конечной стальной продукции выполняется обработка сляба (промежуточная стальная заготовка в виде плиты) на прокатном стане (агрегат, в котором происходит последовательная пластическая деформация металла при сдавливании его между вращающимися валками), на выходе которого получаем тонкую стальную полосу. В данном случае возможно оптимизировать сразу в нескольких направлениях:
повысить производительность прокатного стана за счет увеличения скорости прокатки заготовки от начала до конца стана;
повысить качественные свойства продукции за счет адаптивного подбора режимов обработки.
С точки зрения математической постановки задачи каждое из направлений может формализоваться в виде отдельной критериальной функции
и
.
Далее рассмотрим ряд подходов и библиотек для решения поставленной задачи.
Декомпозиция оптимизации
Если постановка задачи позволяет свести исходную задачу многокритериальной оптимизации к двум параллельным независимым или последовательным зависимым однокритериальным задачам оптимизации, то можно воспользоваться этим фактом, а далее решать задачу с помощью подходов для однокритериальной оптимизации.
Пример
Продолжая пример с прокатным станом. Здесь много вариаций, как мы можем выполнить декомпозицию. Вряд ли в данном случае существует возможность сформировать независимые задачи (отдельно по качеству и производительности). Первые варианты, которые приходят в голову:
оптимизировать качество при ограничении на производительность или наоборот;
последовательно, т.е. оптимизировать качество, затем при найденных параметрах для оптимизации качества решать задачу по производительности.
Для примера рассмотрим декомпозицию на последовательные зависимые задачи. Запишем исходную задачу:
Запишем первый шаг в декомпозиции задачи:
и второй шаг с учетом полученного управления :
где "*" подчеркивает, что данные параметры зафиксированы, и — преобразованная целевая функция
. Переход к однокритериальной оптимизации позволяет воспользоваться более изученным и богатым аппаратом оптимизации. Но применение декомпозиции не всегда возможно, а если переход получается выполнить, то чаще всего это приводит к ограничению общности задачи.
Методы из коробки
Pymoo
Python библиотека pymoo специализируется на задаче многокритериальной оптимизации. Библиотека обладает большой функциональностью:
многокритериальная оптимизация;
однокритериальная оптимизация;
поддержка линейных и нелинейных ограничений;
примеры с хорошо известными задачами;
поддержка специальных классов задач: бинарные, дискретные и смешанные;
визуализация решений.
Optuna
В блоке однокритериальной оптимизации мы уже обращались к данной библиотеке, но есть и поддержка многокритериальной оптимизации с ранее описанными плюсами и минусами.
Резюме
На практике мы чаще стараемся сформировать постановку задачи в однокритериальной постановке для того, чтобы упростить решение обратной задачи. Совсем замечательно, если получается перейти к решению задачи линейного программирования. Во второй статье мы перейдем к рассмотрению предложенных ранее постановок на реальных ML-задачах / в рамках конкретной задачи машинного обучения.
Сокращения
БО — байесовская оптимизация;
ЛП — линейное программирование;
СЦЛП — смешанное целочисленное линейное программирование.
Ссылки на статьи и материалы
Помощник сталевара: для чего металлургам нужно машинное обучение?
Методы оптимизации в примерах и задачах - Пантелеев А.В., Летова Т.А.
Б.Т. Поляк. Введение в оптимизацию, Наука, 1983.
Обзор методов численной оптимизации. Безусловная оптимизация: метод линий
Спасибо DS-команде центра машинного обучения компании «Инфосистемы Джет» в подготовке материалов.