Привет, Хабр! Меня зовут Мария Белялова, и я занимаюсь data science в мобильном фоторедакторе Prequel.
Эта статья открывает наш цикл материалов со сравнением алгоритмов оптимизации для обучения нейросетей. Помимо классических методов, которые давно зарекомендовали себя, мы рассмотрим и менее известные методы, и совсем новые: например, алгоритм MADGRAD, разработанный в Facebook в этом году. В первой статье мы сравним поведение алгоритмов на тестовых функциях, во второй — посмотрим, как они ведут себя на игрушечной задаче по распознаванию цифр из датасета MNIST, а в третьей — проверим эти алгоритмы в бою на реальной задаче из продакшена.
Методы оптимизации используются для нахождения экстремумов функций. Обучение нейросети представляет собой не что иное, как оптимизационную задачу, так как во время него минимизируется функция потерь. Существуют аналитические и численные методы оптимизации. В машинном обучении редко встречаются аналитические формулы, в большинстве случаев задачи решаются численно. Численные методы, в свою очередь, подразделяются на прямые и итерационные. Прямые методы — это алгоритмы, позволяющие получить решение за конечное число арифметических действий. Итерационные методы — это алгоритмы, в которых решение получается как предел при стремлении числа итераций n к бесконечности. При конечных n получаются приближенные решения.
В этой статье мы рассматриваем итерационные градиентные методы (а также методы, которые используют производные более высокого порядка), которые используются для обучения нейросетей. Мы предполагаем, что читатель уже знает, как нейронные сети обучаются с помощью градиентного спуска.
Существует большое количество различных алгоритмов, так как все методы обладают теми или иными недостатками (о которых мы поговорим дальше). На практике вряд ли кто-то будет сравнивать все доступные алгоритмы оптимизации, так как это очень затратно по времени. Обычно при обучении нейросетей инженеры выбирают среди нескольких самых популярных алгоритмов оптимизации, таких как Adam, SGD и RMSprop, которые реализованы в современных фреймворках для глубинного обучения. В своем эксперименте мы решили сравнить все алгоритмы оптимизации, реализованные во фреймворке PyTorch, все алгоритмы из пакета torch-optimizer, а также новый алгоритм оптимизации MADGRAD от Facebook — итого 39 штук.
Почему существует так много алгоритмов оптимизации?
Методы оптимизации нейросетей можно поделить на две группы: методы первого порядка и методы второго порядка. Для того, чтобы сделать следующий шаг, методы первого порядка используют информацию о градиенте, а методы второго порядка используют гессиан или его аппроксимацию. К методам второго порядка относятся, например, L-BFGS, Shampoo, Adahessian, Apollo. С одной стороны, эти методы мощнее методов первого порядка, и часто обладают лучшей сходимостью. С другой стороны, многие методы второго порядка очень медленные и занимают много памяти (но не все). По этой причине они редко применяются на практике.
В алгоритмах оптимизации нейросетей широко используются различные адаптивные подходы для упрощения процедуры поиска гиперпараметров, с которыми алгоритм приведет к наилучшим результатам. В таких методах используется адаптивный learning rate. В отличие от SGD-подобных методов (таких, как SGD c моментом, которые используют глобальный learning rate для всех параметров), адаптивные методы вычисляют свой learning rate для каждого параметра. К адаптивным методам относятся Adam, Adagrad, AdaDelta, RMSProp. Обычно адаптивные методы сходятся быстрее, но обладают худшей обобщающей способностью (например, на таких больших датасетах, как ImageNet). Некоторые методы (AdaBound, AdaBelief, SWATS) пытаются объединить преимущества обоих подходов. Существуют алгоритмы для быстрого обучения нейросетей с большим размером батча, такие как LARS и LAMB. Часто случается так, что какой-либо метод хорош для одной задачи, но в другой задаче работает плохо, и поэтому придумывают модификацию этого метода для новой задачи (например, у LARS плохой перфоманс на BERT, поэтому придумали LAMB). Существует мета-алгоритм Lookahead, который является оберткой для других алгоритмов оптимизации. Он позволяет выявить направление, в котором двигался внутренний алгоритм в течение k итераций, и сделать шаг с некоторым множителем в направлении от весов, которые были на итерации n, к весам, которые были на итерации n + k.
Так как количество рассматриваемых алгоритмов слишком велико, мы не будем подробно останавливаться на математическом разборе каждого из них.
Ссылки на статьи с методами, которые рассматриваются в этой статье
Поведение алгоритмов на тестовых функциях
Существует целый набор тестовых функций, специально разработанных для анализа поведения алгоритмов оптимизации на различном ландшафте. Тесты разработаны так, чтобы показать слабые места алгоритмов в ситуациях с седловыми точках, в локальных минимумах, в долинах. Для своих тестов мы выбрали две наиболее популярные функции — Розенброка и Растригина. Код для визуализаций взят из репозитория torch-optimizer.
Функция Розенброка — это невыпуклая функция, которая задается формулой 
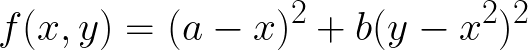. В нашем примере выбраны значения параметров 
.У неё есть один глобальный минимум в точке
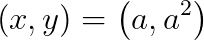. Он находится в длинной, узкой, параболической плоской долине. Для алгоритмов оптимизации саму долину найти тривиально, а вот сойтись к глобальному минимуму сложно.
Функция Растригина — это невыпуклая функция,которая в n-мерном случае задаётся формулой
, где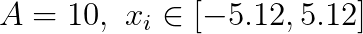 
. У неё есть один глобальный минимум в точке 
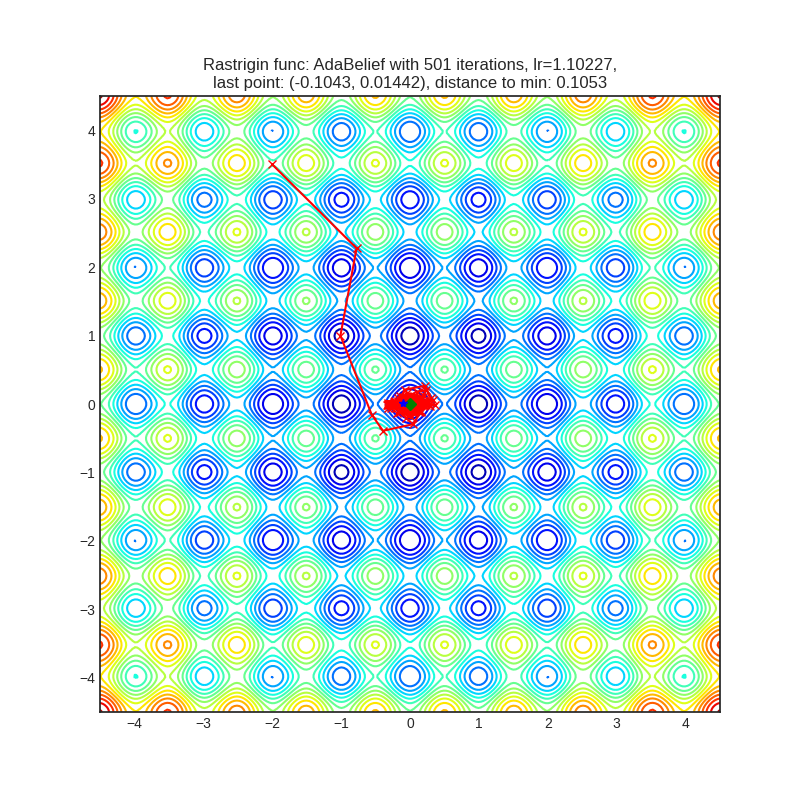
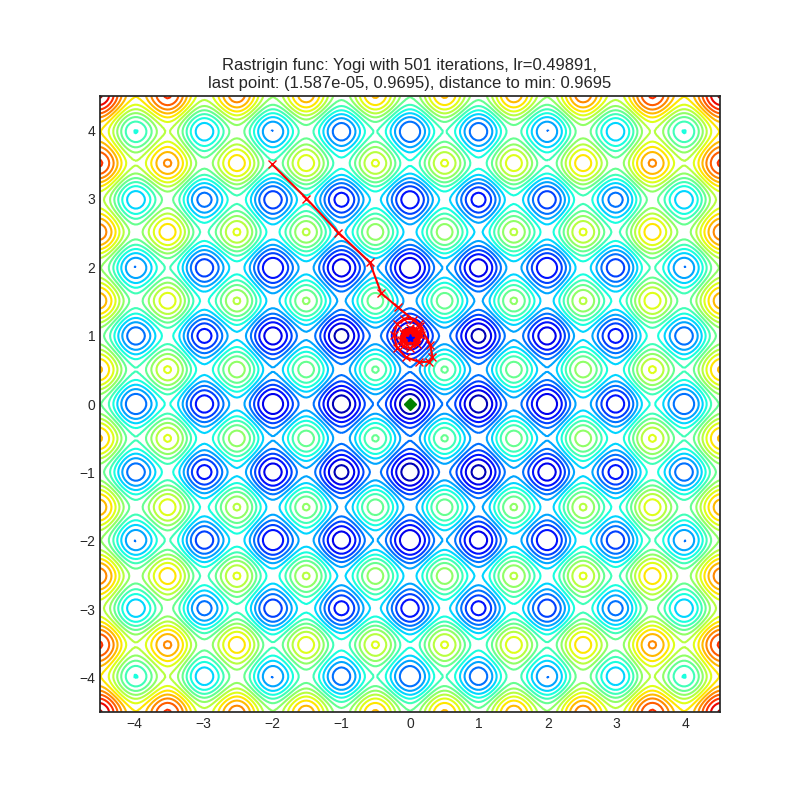
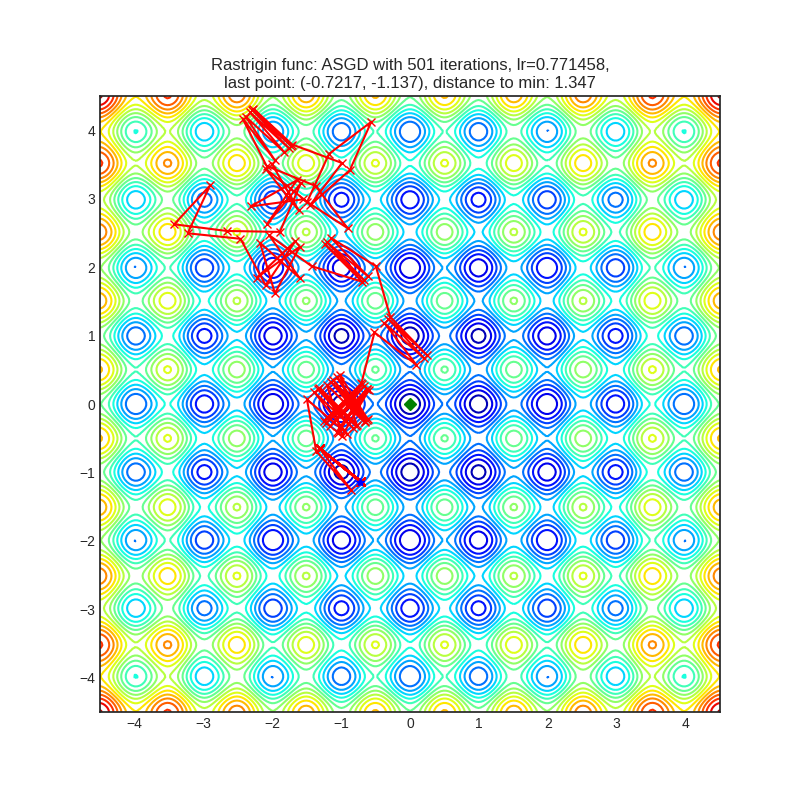
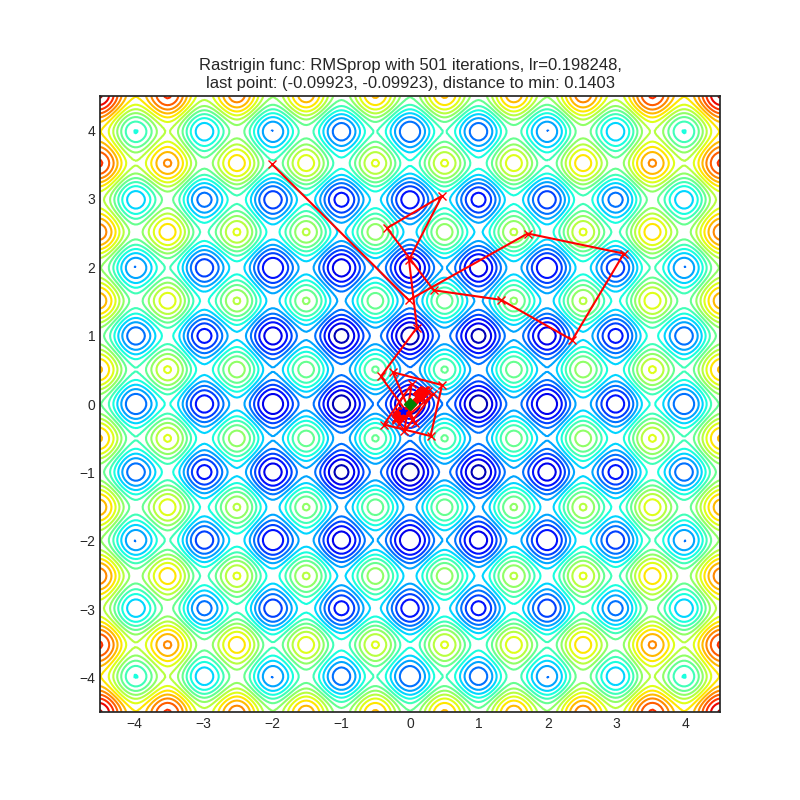
(ниже рассматривается случай для n = 2). Этот минимум сложно найти из-за большого пространства поиска и из-за большого количества локальных минимумов.Мы решили, что приводить графики всех 39 алгоритмов оптимизации бессмысленно, поэтому далее мы сгруппируем все алгоритмы по одному признаку. Так как в тестовых функциях мы знаем точку глобального минимума, то этим признаком стало расстояние от точки останова алгоритма до глобального минимума. Также мы проиллюстрируем поведение каждой группы на графиках. Красной линией обозначен путь, зеленой точкой — глобальный минимум, а синяя точка — точка останова алгоритма.
- Максимально приблизились к глобальному минимуму. Для функции Розенброка это алгоритмы с расстоянием меньше 0.3, для функции Растригина — меньше 0.2 — те, что остановились в районе глобального минимума, а не в локальных.
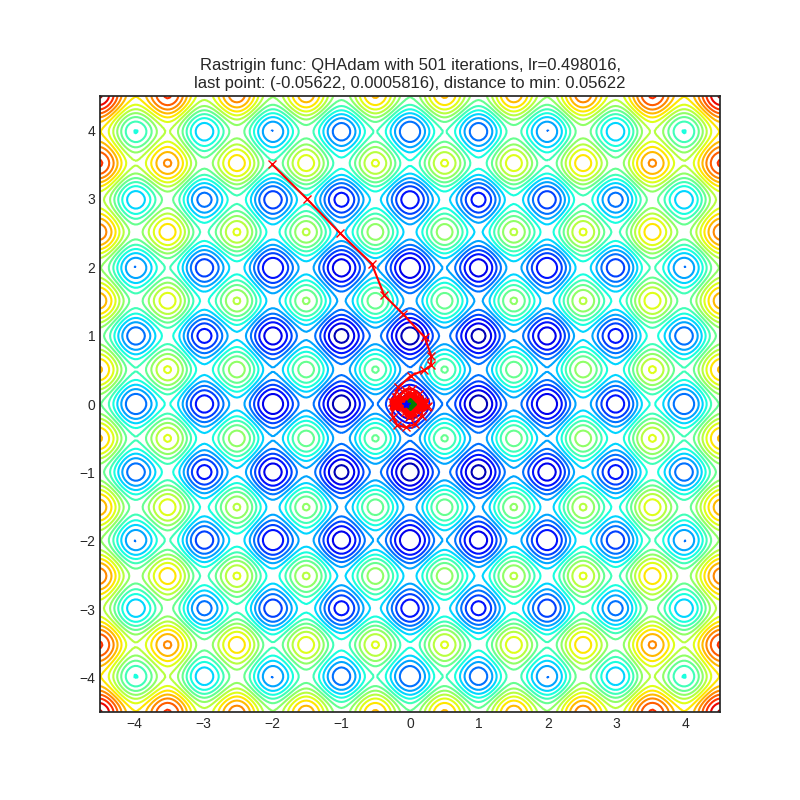
- Продвинулись к глобальному минимуму. Функция Розенброка: смогли преодолеть перегиб в параболической долине, функция Растригина: смогли уйти дальше ближайшего локального минимума.
a. Проходили мимо глобального минимума, но остановились не в нём.
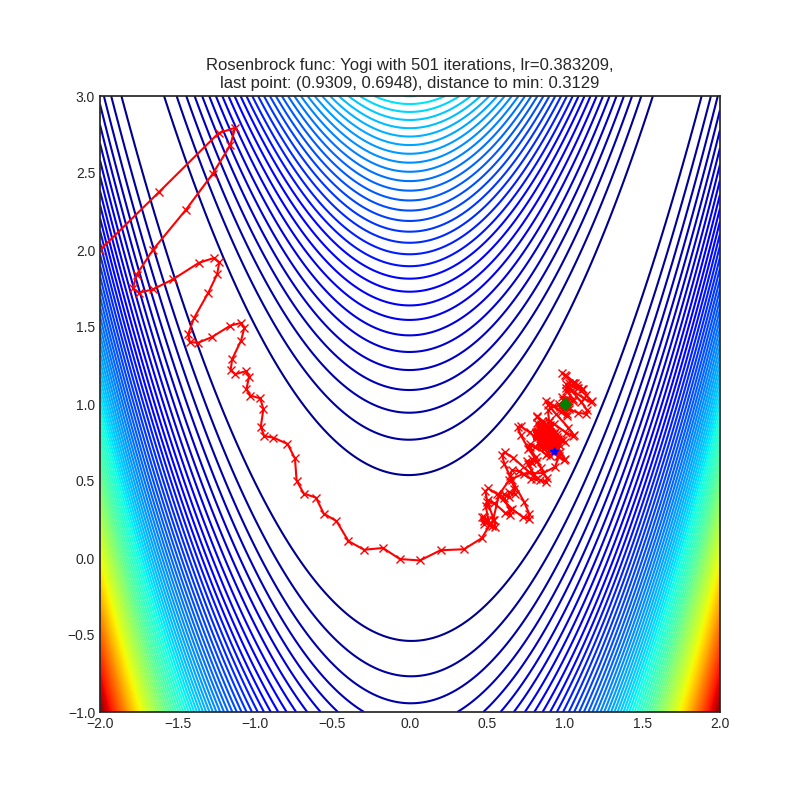
b. Не доходили до глобального минимума.
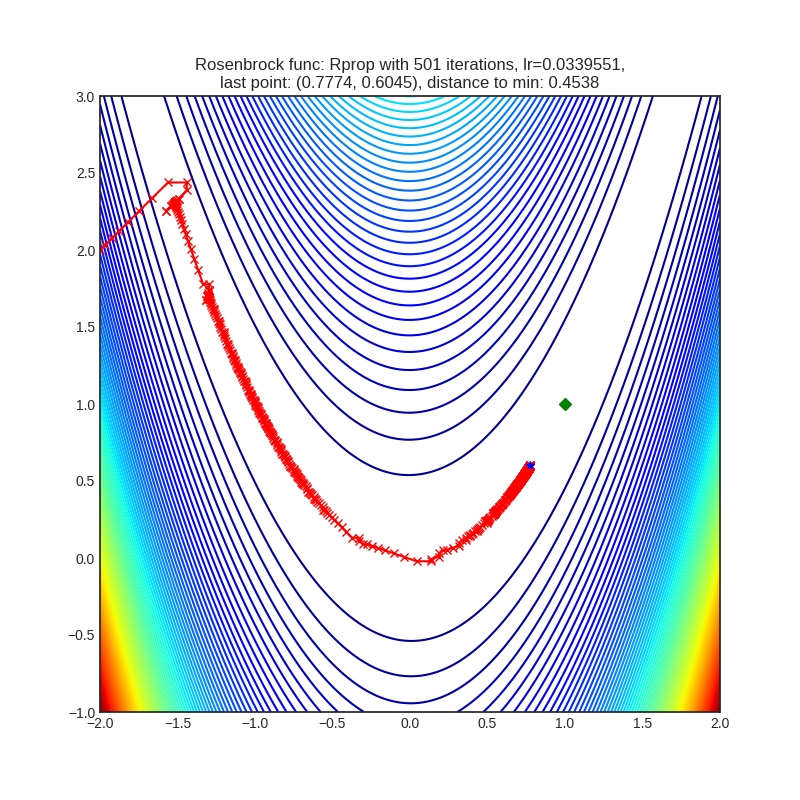
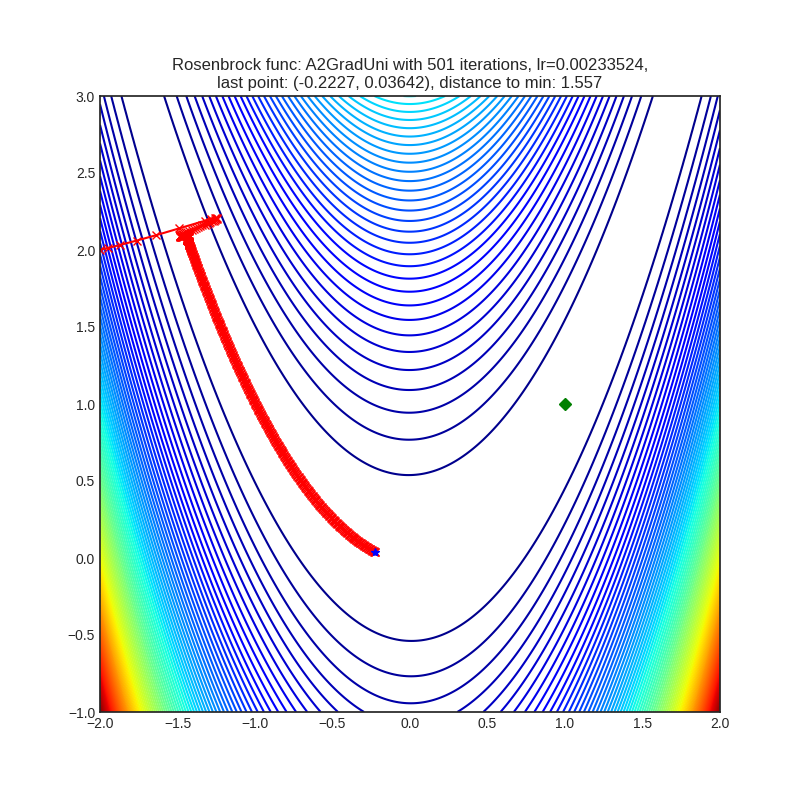
- Не смогли далеко продвинуться. Функция Розенброка: не смогли преодолеть перегиб в параболической долине, функция Растригина: остановились в ближайшем к стартовой точке локальном минимуме.
Оптимальный learning rate для каждого из оптимизаторов находился с помощью алгоритма оптимизации гиперпараметров Tree-Structured Parzen Estimators (TPE), реализованного в библиотеке hyperopt. Этому алгоритму на вход подается пространство поиска для коэффициента, подобранное вручную для каждого алгоритма оптимизации. Это делается для того, чтобы помочь TPE найти то значение, на котором алгоритм оптимизации сойдется быстрее. На каждой из тестовых функций все алгоритмы делают 501 шаг.
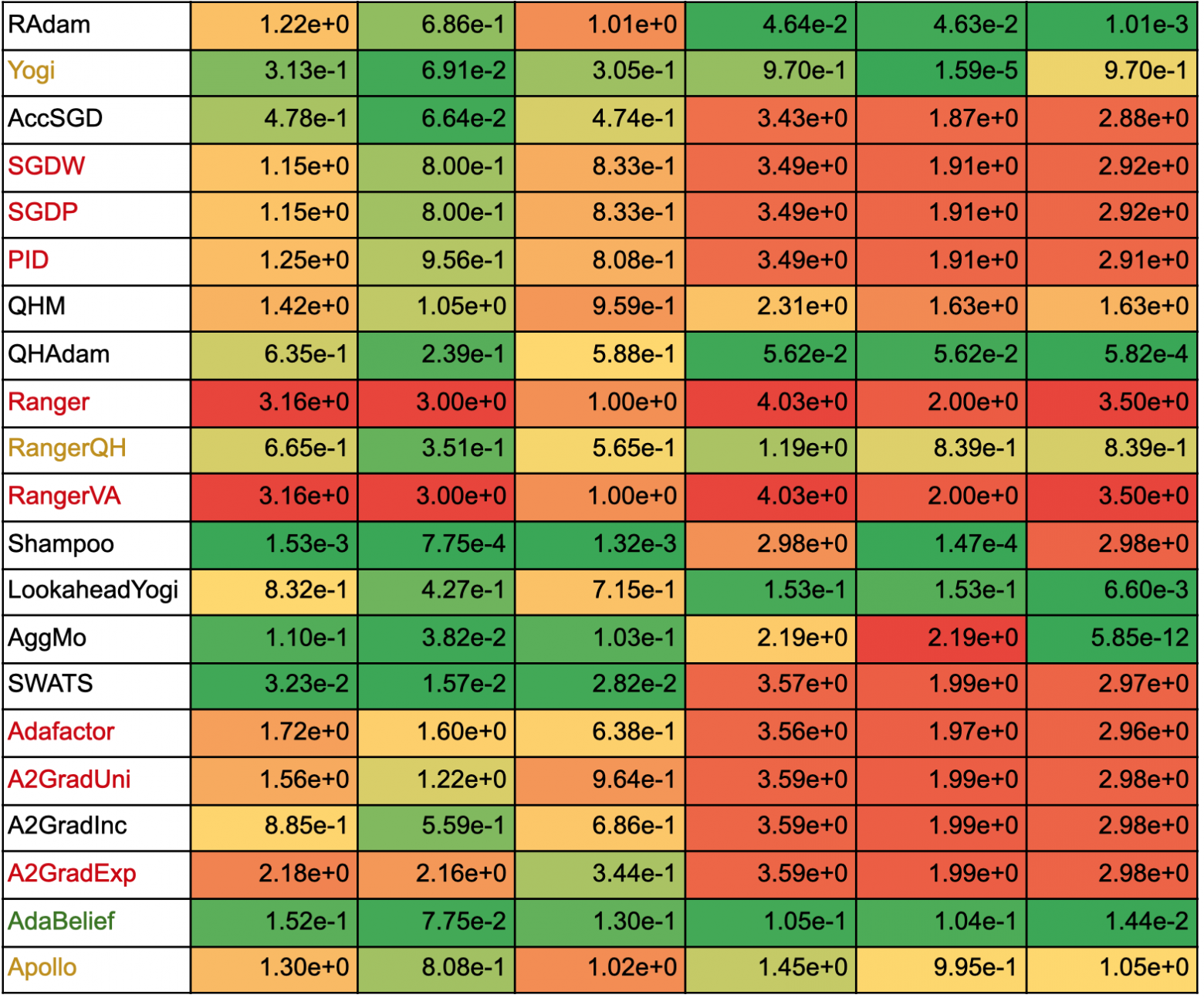
Ниже в таблицах указано, в какие группы попали разные алгоритмы. Зеленым цветом отмечены те алгоритмы, что для обеих функций попали в первую группу, желтым — во вторую, красным — в третью. Здесь важно отметить, что алгоритм не стоит выбирать только исходя из его результатов на тестовых функциях: разные оптимизационные подходы обладают уникальными свойствами и могут быть приспособлены для различных целей, или могут потребовать определенного графика обучения (learning rate schedule).
Таблица с расстояниями от точек останова каждого алгоритма до точек глобального минимума функций Растригина и Розенброка
В таблице ниже указаны расстояния от точек останова до точек глобального минимума для функций Растригина и Розенброка: евклидово расстояние и расстояния по каждой из координат отдельно. Каждый столбец размечен тепловой картой: чем меньше значение, тем ближе оно к зелёному, чем больше значение, тем ближе оно к красному. Для наглядности тепловая карта строится по значениям внутри одного столбца, а не по всей таблице. Цветом выделены названия алгоритмов по тому же принципу, что и в предыдущей таблице.
Интересно понаблюдать, как алгоритмы, преодолевшие ближайший локальный минимум, ведут себя на функции Растригина:
- Некоторые алгоритмы уделяют большое внимание только одной из координат (см. столбцы с расстоянием по х и по y до глобального минимума), например, AggMo, Apollo, MADGRAD, NovoGrad, Lookahead(Yogi):
- Другая группа алгоритмов передвигается сразу по обеим координатам, зачастую минуя все остальные локальные минимумы. Примерами являются AdaBelief, AdaBound, QHAdam, RAdam, Adamax, Yogi (интересно, что Yogi с мета-алгоритмом Lookahead стал передвигаться вдоль одной из координат, но зато смог достичь глобального минимума):
- Часть алгоритмов (QHM, ASGD, RMSProp) передвигается хаотично:
- Остальные алгоритмы совмещают в себе и первую, и вторую тенденцию, например, Adam и AdamW:
На функции Розенброка траектории алгоритмов, достигших лучших результатов, осциллируют в начале, а потом становятся ровнее:
Траектории остальных методов выглядят так:
Среди всех траекторий сильно выделяется путь метода второго порядка LBFGS (первый график выглядит странно из-за масштаба, но в итоге алгоритм нашел глобальный экстремум функции):
При этом, траектории адаптивных методов второго порядка Adahessian, Apollo и Shampoo выглядят более привычно:
Многие алгоритмы ведут себя по-разному на тестовых функциях, которые имеют разные особенности ландшафта. Лишь небольшая группа алгоритмов смогла показать приемлемое качество на обеих тестовых функциях: AdaBelief, AdaBound, Adahessian, Adam. Все эти алгоритмы адаптивные. Среди них есть один метод второго порядка, Adahessian.
Однако, стоит помнить, что при выборе алгоритма для обучения нейросети не стоит полагаться только на тестовые функции. Они не могут показать, как будет вести себя тот или иной алгоритм в гораздо более сложной среде: в примерах выше процесс оптимизации происходит в двумерном пространстве, тогда как при обучении нейросетей размерность пространства существенно выше. К примеру, новый алгоритм MADGRAD не смог дойти до глобального минимума на функции Растригина, но, в целом, ведёт себя адекватно.
В следующих статьях мы собираемся проиллюстрировать работу разных алгоритмов оптимизации на примере игрушечной и реальной задач. Спасибо за внимание!