How to become an author
Search
Write a publication
Pull to refresh

Comments 47

Получается, что хаоса нет? То, что внешне казалось хаосом, имеет строгий внутренний порядок?

А вот интересно, в логистическом отображении хаоса тоже нет? И все последовательности в нём являются периодическими (только их период может быть ОЧЕНЬ большим)?

И множество Мандельброта состоит целиком из сателлитов и точек Мисюревича, и никаких бесконечно тонких нитей в нём нет?

Total votes 4: ↑4 and ↓0+4

Конечно же есть — в статье как раз об этом сказано. То что нелинейная система была склонна к дежавю оказалось интересным подклассом задач детерминированного хаоса. Конкретно для ФПУ можно взять много грузиков, сделать сильнее нелинейность или инициировать систему большими энергиями, и пожалуйста: чистейшая термолизация, белый шум и хаос!

Total votes 4: ↑4 and ↓0+4

Да, но система конечна, детерминирована и в ней нет диссипации. Так что шум и хаос реальны в том же смысле, в каком хороший конгруэнтный датчик случайных чисел выдаёт случайные числа. Эта последовательность может быть сколь угодно длинной, проходить тесты на случайность. Но она не случайна. Это эмуляция случайности.

Total votes 2: ↑2 and ↓0+2
UFO just landed and posted this here
Любой детерминированный алгоритм после X итераций начнёт повторяться. Этот X может быть сколь угодно большим, но он конечен, и его можно вычислить математически.
Total votes 2: ↑1 and ↓10
Это только в том случае, если количество состояний системы конечно.
Total votes 3: ↑3 and ↓0+3

Рискну предположить, что даже если количество состояний - континуум, то система почти всегда будет стремиться к циклическому поведению.

Эта гипотеза возникла у меня при рассматривании множества Мандельброта — если взять и увеличить тонкую нить на отрицательной части вещественной оси (пример видео), то окажется, что она не бесконечно тонкая, а содержит в данной точке сателлит. Это значит, что фазовая траектория не хаотична, а стремится к некоему периоду. Хотя сателлит может оказаться очень маленьким, а период цикла - очень большим, но это именно цикл, а не хаос.

Мне не удалось найти подтверждения или опровержения этой гипотезы, так что она нуждается в проверке, нужно попытаться поискать циклы с помощью длинной арифметики.

Total votes 4: ↑3 and ↓1+2

Есть теорема Пуанкарэ о возвращении, применимо ли это к Мандельброту не знаю.

Total votes 1: ↑1 and ↓0+1
Есть теорема Пуанкаре-Бендиксона, о том, что в двумерном случае предельный цикл — это действительно самое сложное, что может быть в динамической системе, но это относится к системам с непрерывным временем. Для дискретных отображений сложное хаотическое поведение возможно даже для одномерного отображения, но для системы, описываемой дифференциальными уравнениями для возникновения хаоса необходима размерность не менее трех, а также нелинейность
Total votes 2: ↑2 and ↓0+2
Необходимое дополнение (ночью вспомнил) — для систем с непрерывным временем хаос возможен и в двумерной системе, если она не является автономной (т.е. в ней присутствует внешнее возбуждение, сила, явно зависящая от времени)
Осциллятор Дуффинга, хаотический режим (фазовая траектория)
image

image
Total votes 1: ↑1 and ↓0+1
Всё что угодно можно выразить через комбинацию циклов, и Фурье это математически доказал. Равно как и то, что комбинация циклов совсем не обязательно будет циклической. К примеру, у суммы sin(x) и sin(sqrt(2)*x) нет общего периода в силу иррациональности корня из двух.

Любая замкнутая система стремится к вырождению, и у вырожденных систем не так уж и много вариантов для поведения. Однако нужно понимать, что «стремится» и «достигает» — это не одно и то же, и чаще системы стремятся к затуханию, а не цикличности.

Множество Мальдеброта — это пример как раз-таки конечной системы в том смысле, что оно описывается конечным (и довольно простым) уравнением. Если на каждой итерации менять правило расчёта, то мы увидим уже совсем другую картину. И вся современная физика строится на константах — хотя не факт, что в масштабах жизни вселенной эти константы действительно константны.
Total votes 1: ↑1 and ↓0+1

у суммы sin(x) и sin(sqrt(2)*x) нет общего периода

Просто захотелось дополнить, что такие функции называются almost-periodic, у них там свои свойства и теоремы. Простите, не удержался. ;)

Total votes 1: ↑1 and ↓0+1
Достаточно взять таких синусов побольше (со смещёнными фазами), и свойство almost-periodic тоже пропадёт. И белый шум таким образом получить можно, и гауссиана в интеграл Фурье прекрасно раскладывается. И даже x2, хотя лично мне сложно представить двойную производную от дельта-функции Дирака.
Total votes 1: ↑1 and ↓0+1

Я, возможно, сейчас что-то упускаю, но, на сколько помню, сумма любого конченого числа синусоид и их произведений будет almost-periodic.

This comment wasn’t rated yet0
Интеграл Фурье определён на бесконечности. А если говорить о конечном, то если период превышает время жизни вселенной — то довольно непросто его зафиксировать. Опять же это при условии, что система линейна.
This comment wasn’t rated yet0

Моё утверждение не имеет отношения ни к интегралу Фурье, ни к линейности какой бы то ни было динамической системы. Я говорю исключительно о сумме синусоидальных функций.

This comment wasn’t rated yet0
Так интеграл Фурье это тоже сумма синусоидальных функций.
Total votes 2: ↑1 and ↓10
Всё что угодно можно выразить через комбинацию циклов, и Фурье это математически доказал.
Это не совсем так, вполне себе существуют функции, ряды Фурье которых расходятся или сходятся, но не к функции, для которых они являются рядом Фурье
В 1922 г. А. Н. Колмогоров построил пример функции f(x) из L2 (0, 2pi), ряд Фурье которой расходится почти всюду на [0, 2pi]
П. Л. Ульянов, О расходимости рядов Фурье

Кроме того, при практическом нахождении пределов тригонометрических сумм возникают ошибки, котрые нельзя компенсировать, просто увеличивая количество членов, учитываемых в сумме, поэтому требуется использование различных методов регуляризации
Суммирование рядов Фурье
Явление Гиббса

Так что при неосторожном использовании рядов Фурье можно и впросак попасть
Total votes 2: ↑2 and ↓0+2
Да, расходящиеся ряды Фурье существуют. Но лично я в этом не вижу ничего предосудительного — вас же не смущает бесконечно возрастающая функция x2? Равно как и расходящиеся степенные ряды прекрасно используются в комбинаторике и цифровой обработке сигналов.
This comment wasn’t rated yet0

А когда начнёт повторятьсч алгоритм выдачи цифр числа Пи?

Total votes 4: ↑4 and ↓0+4

На каком то знаке память закончиться

Total votes 2: ↑2 and ↓0+2

Цифры числа Пи начнут повторяться, если перезапустить генератор с той же начальной инициализацией (например, тем же начальным номером цифры), что на практике, скорее всего, рано или поздно произойдёт. Поэтому такой генератор не очень практичен. Если бы этот генератор был недетерминированным, цифры бы не повторялись даже при одинаковых начальных состояниях.

Total votes 2: ↑1 and ↓10

Я уверен, что вы сами знаете контрпримеры, только не вспомнили их. Алгоритм вычисления знаков числа пи, например.

Total votes 3: ↑3 and ↓0+3

В приведенном мною примере с конгруэнтным датчиком последовательность не случайна по определению: вы можете в любой момент повторить реализацию один в один, просто задав одно и то же начальное число (Кнут Вам в руки). То же самое относится к детерминированной системе с конечным числом степеней свободы без диссипации. В ней нет случайности по определению, как бы хаотично она себя ни вела в определённые отрезки времени.

По этому поводу хотел бы напомнить известную дискуссию Бора и Эйнштейна. Э считал, что бог Бора играет в кости. Замечательно. Но к тому времени было построено солидное классическое здание молекулярно-кинетической теории. Как по-вашему, почему Э не имел претензий к богу Больцмана или Гиббса? Вот по той же причине. Частицы во вселенной Больцмана подчинялись классическим законам движения. Но их было слишком много (собственно, это "слишком" начинается с 3-х при наличии взаимодействия). Статистические законы позволяют что-то выяснить про такие многочастичные ансамбли, поскольку применить законы классической механики нет никакой фактической возможности (как из-за количества объектов, так и из-за невозможности абсолютно точно задать начальные условия для каждого из них). В целом же вселенная Больцмана вполне себе детерминистична. По этой причине старик Э не имел к ней никаких претензий.

Total votes 6: ↑5 and ↓1+4

нелинейная система была склонна к дежавю

Это как раз и означает, что траектория системы в фазовом пространстве оказалась периодической.

Total votes 1: ↑1 and ↓0+1

Кий не влетает в шары сложенные треугольником. Есть шар-посредник для этого, он же биток. Да и треугольник принято называть пирамидой, даже если шары сложены в виде ромба, как в при игре в "девятку".

Total votes 2: ↑2 and ↓0+2

Ну и, кстати, в обратный процесс тоже вполне можно поверить. Его сложность состоит лишь в том, что чтобы все шары встали обратно в пирамиду придётся сообщить импульс не одному, а аж 15 шарам, и расчёт этих импульсов задача охрененно сложная.

Total votes 1: ↑1 and ↓0+1

Точности изготовления шаров, ровности стола и точности приложения импульсов не хватит, чтобы такое проделать - так что задача собрать из 15 шаров в точную пирамиду и выпульнуть из неё белый шар - на практике не выполнима.

И это касается всех вопросов про стрелу времени - только в теории мы можем что-то посчитать с абсолютной точностью. На практике всегда есть неточности, которые разрушат "обратное движение".

Да и второй закон термодинамики неумолим: "прямое" движение всегда превращает механическую энергию в тепловую - исключений нет даже в вакууме космоса (превращение идёт, хоть и медленно, через поглощение, отражение и излучение). А промотка в "обратном" направлении всегда будет давать обратный эффект: сила трения ускоряет шары! Вспоминаем фильм "Довод"!

Total votes 9: ↑9 and ↓0+9

а прикольно было б попробовать настроить 15 катапульт для получения такого эффекта

Total votes 2: ↑2 and ↓0+2

Действительно интересно, спасибо!

Total votes 1: ↑1 and ↓0+1

Идеальный перевод! Спасибо!

Наконец рувдс начал брать хороших авторов, вместо Гугл транслейт.

Total votes 8: ↑8 and ↓0+8

Мне одно место захотелось улучшить (это не совсем к переводу вопрос, но всё же):

Основываясь на исследованиях (...) проведенных в конце 1960-х годов Борисом Чириковым, Эдди Коэн из Рокфеллеровского университета...

Коэн из Рокфеллеровского университета, а Чириков как будто сам по себе. Неплохо было бы напомнить, что он работал в Новосибирске, в Институте ядерной физики Сибирского отделения АН СССР.

Total votes 1: ↑1 and ↓0+1

Спасибо, добавил ссылку на википедию. Если б вы не заострились, то имя соотечественника так и затерялось бы в этой эстафете исследователей

Total votes 1: ↑1 and ↓0+1
> Теперь прокрутите плёнку в обратном направлении. Движение мячей выглядит совершенно естественно,

это только «выглядит». на самом деле при прокрутке пленки назад шары после столкновения разбегаются быстрее, чем до столкновения. а все потому что в реалии шары до, во время и после столкновения теряют энергию — на трение качения, на нагрев при соударении, на преодоление сопротивления воздуха. так что как ни крути пленку вперед или назад, всегда можно отличить вперед она движется или назад.
Total votes 5: ↑5 and ↓0+5
Приятно читать статью, которая написана и переведена людьми, которые действительно понимают, о чём пишут и что переводят. Большая редкость в наше время.
Total votes 6: ↑6 and ↓0+6

как замечательно, что теперь у нас есть мощные машины для таких расчетов.

как грустно, что их мощность все еще не бесконечна.

Total votes 3: ↑3 and ↓0+3
Мэри Цингу, которая, хотя и не является автором отчёта, внесла значительный вклад в работу

Она является полноценным соавтором работы, т.к. на титульном листе того самого отчета LA-1940 написано


Work done by:
E. Fermi
J. Pasta
S. Ulam
M. Tsingou

Report written by:
E. Fermi
J. Pasta
S. Ulam

И, кстати, последние лет 15 в научных статьях всё чаще часто можно встретить, что цепочку FPU принципиально называют цепочкой FPUT в целях "восторжествования справедливости".

Total votes 1: ↑1 and ↓0+1

Мари Цингу делала программы на MANIAC — теперь хочется найти эмулятор этой машины!


Коды древних

Total votes 5: ↑5 and ↓0+5
Хорошая статья, как и всегда. Интересно, что описанная цепочка осцилляторов — не единственная модель подобного рода. Есть еще, например, цепочка Тоды — система, в которой возвращающая нелинейная сила для каждой из колеблющихся частиц зависит от двух соседей экспоненциально
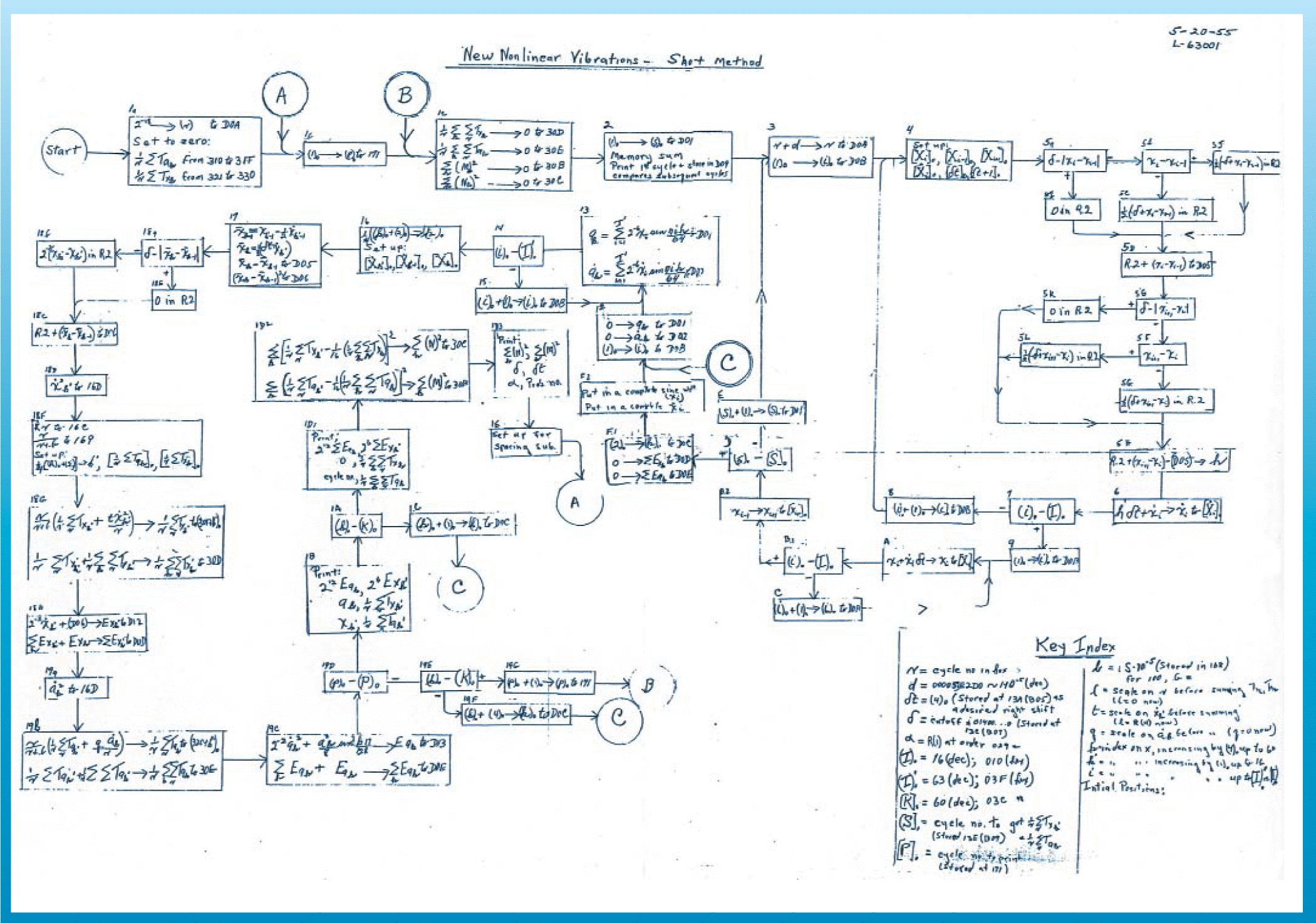
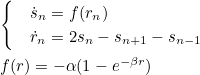
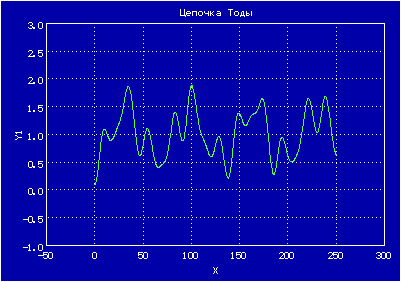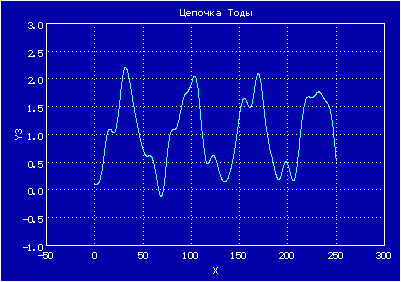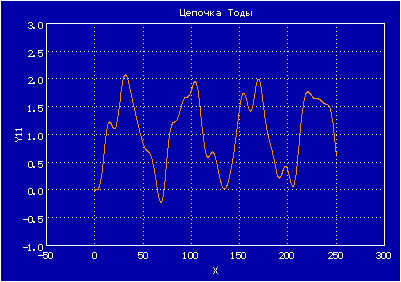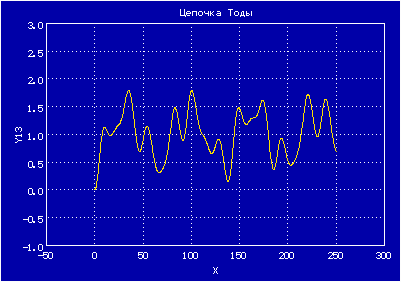
image

Цепочка Тоды, 7 осцилляторов, графики колебаний
image

Эта модель также ведет себя хаотически, и в ней в пределе при n, стремящемся к бесконечности, можно наблюдать уединенные волны — солитоны

Нелинейная решетка (цепочка Тоды). М. Тода. (стр.163)
Total votes 1: ↑1 and ↓0+1

Пример про "вибрацию луча" как-то совсем непонятен... Вообще, что такое вибрация луча? Кто вибрирует - сам луч или тело, на которое он падает?

"Вибрация луча вызывает уменьшение отражаемого им света" - здесь "им" относится к самому лучу или к чему-то другому?

"Через несколько десятков миллисекунд вибрация становится локализованной в массиве лучей, что приводит к появлению тёмной горизонтальной линии" - Какой массив лучей имеется здесь в виду?..

Total votes 2: ↑2 and ↓0+2

Лучи — в смысле отдельные сегменты гребенки на пластинке. На картинке видно что из пластинки выходят микробалки-лучи, вибрации которых фиксируются отраженным светом

Total votes 1: ↑1 and ↓0+1
Sign up to leave a comment.

Your account

Sections

Information

Services

Support
© 2006–2024, Habr