Меня зовут Дима, я разработчик библиотеки ETNA в Тинькофф. Расскажу о том, как в задаче прогнозирования временных рядов появляются стратегии, какими они бывают и как воспользоваться стратегией в библиотеке ETNA.
Откуда появляются стратегии прогнозирования
В отличие от задач машинного обучения на статических данных, в прогнозировании временных рядов есть важная особенность: в качестве признаков мы почти всегда используем предыдущие значения ряда. Эти признаки называют лагами — мы рассказывали про них раньше:
Посмотрим, как использование лагов в качестве признаков влияет на процесс прогнозирования.
Например, нужно научиться предсказывать спрос на яблоки на следующий день. Есть таблица с данными о продажах. В первой строке — номер дня, во второй — количество проданных яблок:

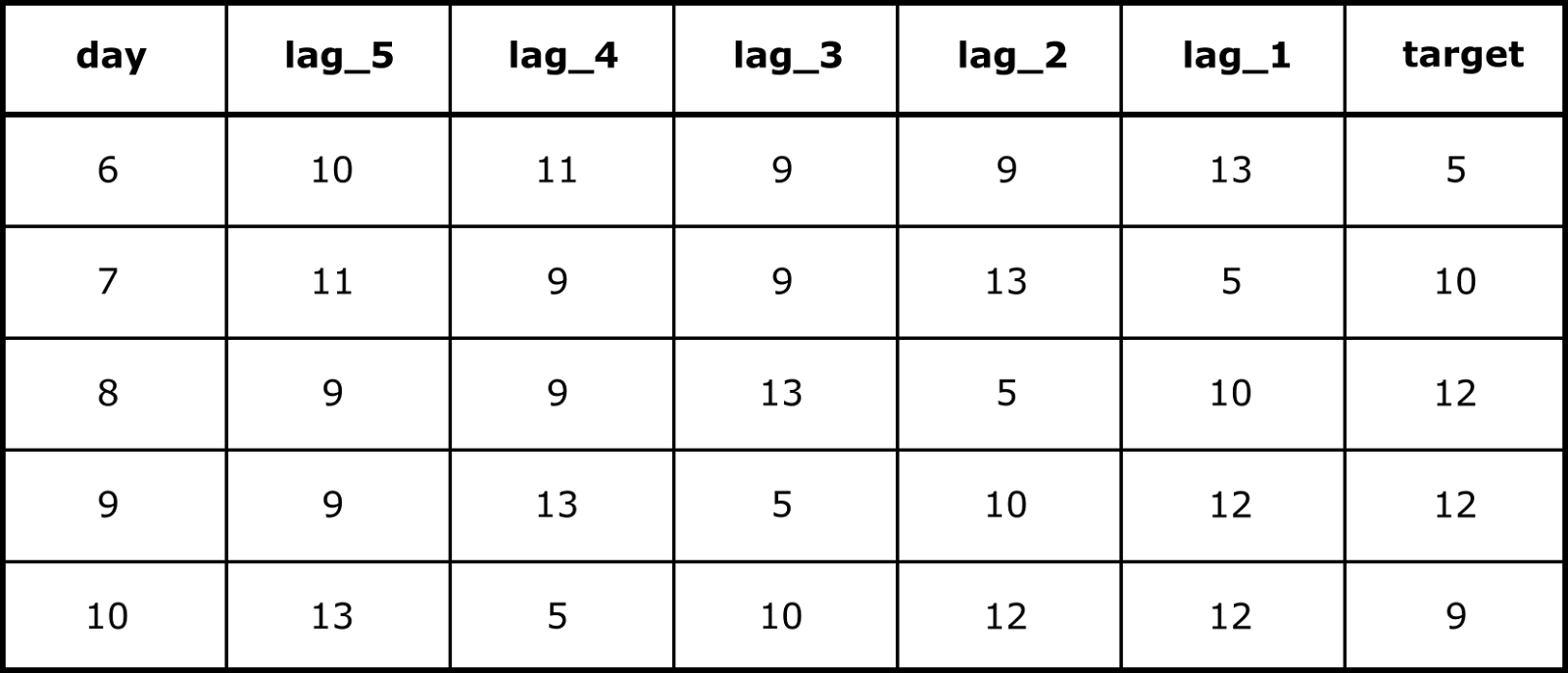
Для предсказания соберем значения за пять предыдущих дней в таблицу для обучения ML-модели:
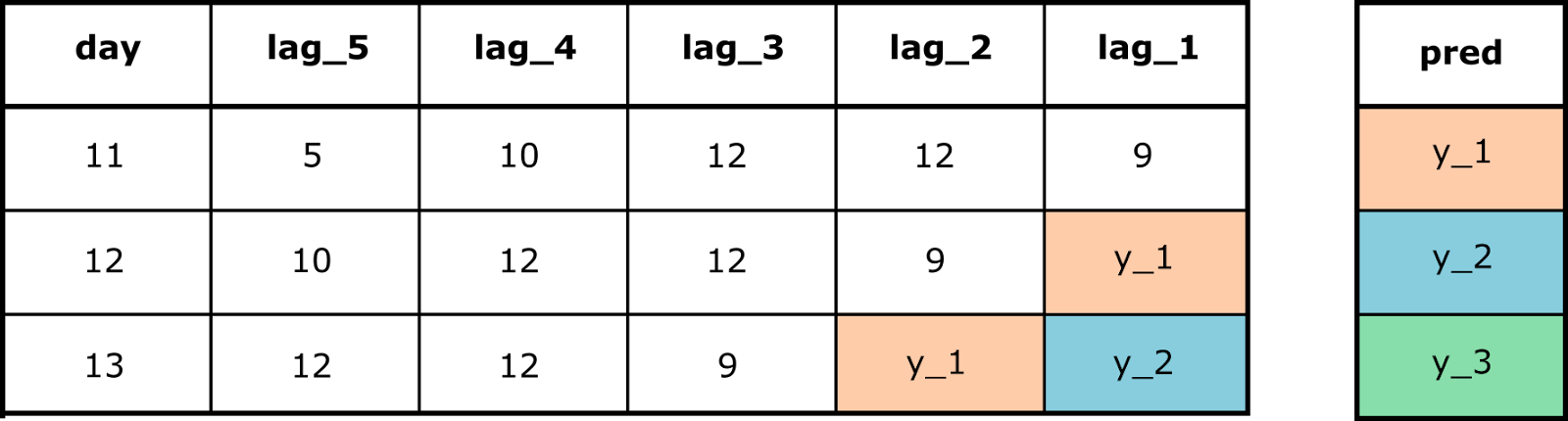
Посмотрим, как модель можно применить для предсказания на день 11:
В конце дня 10 получаем данные за последние пять дней: [5, 10, 12, 12, 9].
Формируем вектор признаков для нашей ML-модели.
Выполняем предсказание на день 11.
Отдаем предсказание заказчику.
Кажется, все просто. Но часто случается так, что предсказаний на один день вперед недостаточно. Можно быстро принять решение об увеличении поставок яблок, но мгновенно увеличить сами поставки не получится. Будет какая-то задержка.
Например, поставки яблок можно увеличить только через три дня. Тогда, чтобы предсказать продажи через эти три дня, достаточно будет избавиться от столбцов lag_1, lag_2 в обучающих данных. Во время предсказания мы будем брать значения за последние три дня и использовать их как признаки lag_3, lag_4, lag_5.
А если хотим получить предсказания за весь промежуток дней с 11-го по 13-й? Получается, что желаемый горизонт прогнозирования стал три дня и изначальный алгоритм с предсказанием только одного значения теперь не подходит.
Стратегиями прогнозирования называются различные подходы к расширению алгоритма на случай, когда горизонт прогнозирования больше одного шага.
Какими бывают стратегии прогнозирования
Начнем со стратегий, которые можно применять для моделей, где предсказание — число. Практически все модели из библиотеки scikit-learn именно такие, работу с вектором чисел там можно сделать только через специальные обертки из модуля multioutput.
Рекурсивная стратегия заключается в том, чтобы взять модель, обученную предсказывать на шаг вперед, и последовательно применять ее шаг за шагом, пока не будет достигнуто предсказание на нужное число шагов. Уже начиная со второго шага вместо истинных лагов начинаем использовать предыдущие предсказания модели. Данные для предсказания будут выглядеть так:
Стратегия простая для понимания и позволяет прогнозировать на неограниченный горизонт. Потенциальная проблема подхода в том, что с каждым шагом все большую долю признаков будут занимать предсказания вместо истинных значений, это может приводить к накоплению ошибок.
Прямая стратегия заключается в том, чтобы выучить отдельную модель на каждую точку горизонта. В нашем примере это дает три модели: для прогнозирования на один день вперед, на два дня и на три дня.
Каждая модель следит за тем, чтобы принимать на обучение столько лагов, сколько будет доступно на момент ее применения. Например, модель для прогнозирования на два дня вперед не может использовать lag_1, но может использовать lag_2 и выше.
Обучить три модели реально, но что делать, когда горизонт 366 шагов? Если взять первую модель с яблоками, обученную без lag_1 и lag_2, то ей можно предсказывать и 11-й, и 12-й дни, просто часть данных придется проигнорировать. Вот так будут выглядеть данные для предсказания модели на три дня:

Назовем такую стратегию упрощенной прямой. Но можно пойти еще дальше. Давайте найдем промежуточную ситуацию между одной моделью на все шаги и отдельной моделью на каждый шаг.

Разобьем горизонт прогнозирования на непересекающиеся промежутки, где за предсказание каждого промежутка горизонта будет отвечать отдельная модель. Получится, что чем ближе к концу горизонта прогнозирования, тем меньшее число лагов можно использовать.
В отличие от рекурсивной стратегии, проблем с накоплением ошибок не будет, потому что все предсказания делаются независимо. Минус прямой стратегии в том, что полученные предсказания разных моделей могут получаться несогласованными. Например, на обучающих данных может присутствовать определенная зависимость между предсказаниями на первый и второй день, но мы не можем гарантировать сохранение этой зависимости в рамках прогноза прямой стратегии.
Гибридная стратегия комбинирует две предыдущие. Мы по-прежнему учим одну модель на каждый шаг, но вместо того, чтобы игнорировать в модели лаги, которые ей недоступны, мы используем предсказания предыдущих моделей. Модели будут использовать для предсказаний такие наборы данных.



Такой подход решает проблему прямой стратегии с согласованностью ответов, потому что у нас есть возможность выучить их зависимости. Кроме того, проблема накопления ошибок будет не так выражена, потому что пробрасывание предсказаний будет происходить и во время обучения. К минусам можно отнести сложность схемы и ее имплементации.
Кроме моделей, которые предсказывают число, есть модели, способные предсказывать сразу вектор. Например, такое просто сделать при помощи нейронных сетей. В таком случае модель может за один шаг спрогнозировать сразу все точки горизонта.
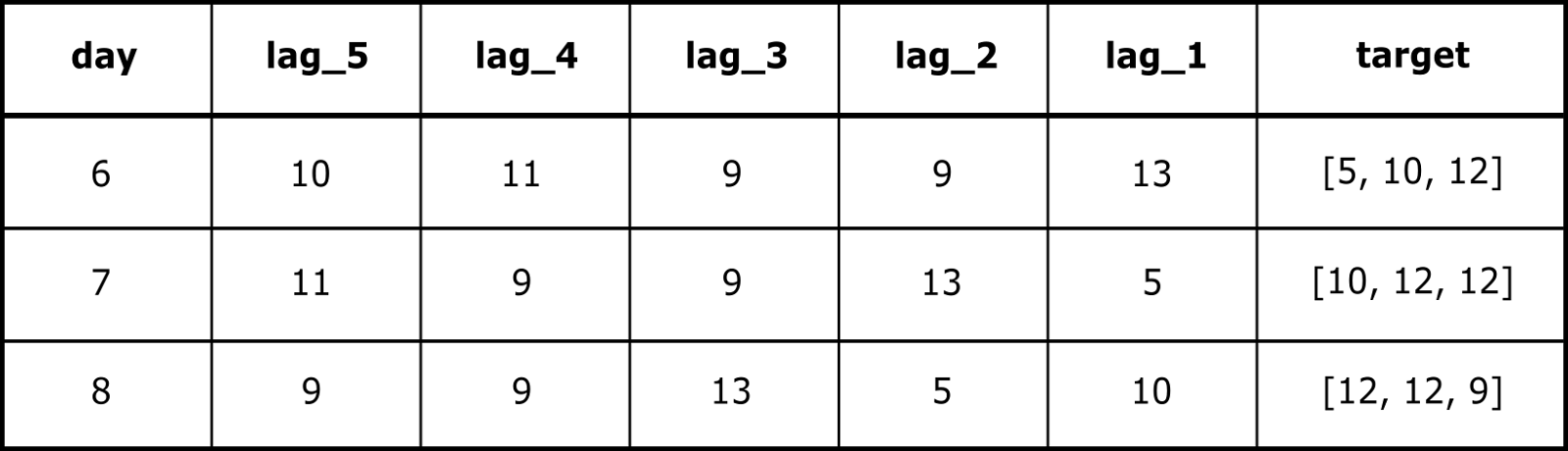
Векторная стратегия позволяет выучивать зависимости предсказаний и не сталкивается с проблемой накопления ошибок, потому что используется только одна модель и один шаг прогнозирования. Но если горизонт большой, качество прогноза может ухудшаться из-за того, что одна модель должна предсказывать и близкие, и далекие точки. Посмотрим, как выглядели бы обучающие данные для такой модели:
Комбинированная стратегия — когда используются несколько стратегий вместе. Можно сделать прямую стратегию на часть горизонта, а потом применять ее рекурсивно. Или выучить несколько отдельных векторных моделей и применять их раздельно на каждый промежуток горизонта, как в прямой стратегии.
Итоги по перечисленным стратегиям соберем в таблицу:

Стратегии прогнозирования в ETNA
Стратегии, доступные в библиотеке ETNA:
Упрощенная прямая, реализуемая при помощи
Pipeline: обучается одна модель, которая использует лаги, доступные для предсказания на весь горизонт.Рекурсивная, реализуемая при помощи
AutoRegressivePipeline: обучается одна модель и применяется рекурсивно.Прямая, реализуемая при помощи
DirectEnsemble: собирается ансамбль из пайплайнов с разными горизонтами прогнозирования и при сборке итогового предсказания во время каждого шага берется ответ от пайплайна с наименьшим горизонтом.
Разберем на примере. Используем вариацию датасета из статьи The tourism forecasting competition, где исследовались различные методы для прогнозирования спроса на туристические направления в Австралии. Полученный датасет искусственный и имеет другие временные метки для выравнивания всех сегментов по времени.
Первые строчки вывода описания датасета:
У нас месячная сезонность, 366 сегментов и 333 месяца. Соберем простой пайплайн для горизонта прогнозирования в 24 месяца и оценим его качество по метрике SMAPE на трех фолдах.
Представим, что в процедуре ретротестирования мы уменьшаем горизонт прогнозирования в несколько раз и во столько же раз увеличиваем количество фолдов. В таком случае мы охватываем все тот же промежуток времени, что и в исходной версии, а потому средние значения SMAPE исходной версии и измененной можно сравнивать.
С помощью этого приема посмотрим, что происходило бы с интересующей нас метрикой, если бы мы уменьшали горизонт прогнозирования для выбранного выше пайплайна и увеличивали количество доступных лагов. К нашей удаче, число 24 удобно для такой процедуры:
Значение метрики SMAPE и продолжительность запуска в секундах при изменении горизонта:
horizon | SMAPE | time |
24 | 27.03 | 42.56 |
12 | 23.13 | 116.11 |
6 | 22.58 | 267.95 |
4 | 22.42 | 416.23 |
3 | 22.37 | 797.69 |
2 | 21.70 | 865.85 |
1 | 20.79 | 1832.43 |
Следующим шагом изучим поведение рекурсивной стратегии. В нашей реализации есть параметр step. Чтобы понять его предназначение, вспомним, что в рекурсивной стратегии мы итеративно предсказываем на один шаг вперед.
Но можно предсказывать не на один, а, например, на два шага. Это приведет к тому, что мы отказываемся от лагов первого порядка, но уменьшаем число итераций вдвое.
В эксперименте посмотрим, что будет происходить с метриками качества при уменьшении параметра step. Чем меньше step, тем больше итераций нам потребуется провести:
Значение метрики SMAPE и продолжительность запуска в секундах для рекурсивной стратегии в зависимости от параметра step:
step | SMAPE | time |
24 | 27.03 | 43.87 |
12 | 25.75 | 63.85 |
6 | 25.68 | 98.32 |
4 | 25.74 | 117.54 |
3 | 25.89 | 131.95 |
2 | 25.69 | 147.11 |
1 | 25.39 | 223.88 |
При step=24 мы имеем упрощенную прямую стратегию. Видим, как метрика несколько улучшилась, когда стали уменьшать параметр step, но после 12 разница уже не выглядит существенной. Временные затраты с уменьшением параметра растут, так как во время предсказания требуется делать больше итераций.
Осталось сравнить это с работой прямой стратегии. Проведем эксперимент по разделению горизонта на несколько равных частей, чтобы использовать по модели на каждую часть:
Значение метрики SMAPE и продолжительность запуска в секундах для прямой стратегии в зависимости от параметра horizon_step:
horizon_step | SMAPE | time |
12 | 25.44 | 116.03 |
6 | 25.41 | 200.72 |
4 | 25.31 | 307.95 |
3 | 25.35 | 411.10 |
2 | 25.24 | 622.60 |
1 | 25.09 | 1366.99 |
После horizon_step=12 улучшения если и были, то совсем небольшие. Также заметно, что при horizon_step=1 удалось добиться наименьшей метрики среди всех испытанных стратегий, но это потребовало более внушительных временных затрат. В отличие от предыдущего случая, здесь время растет значительнее с изменением параметра. Время получается пропорциональным количеству обучаемых моделей.
Выбор конкретной стратегии уже зависит от требований заказчика. Сведем наиболее интересные результаты в таблицу:
Подход | SMAPE | Время, с |
| 27.03 | 43 |
| 25.75 | 64 |
| 25.39 | 224 |
| 25.44 | 116 |
| 25.09 | 1367 |
Итоги
Мы рассмотрели предпосылки для введения различных стратегий прогнозирования временных рядов. Посмотрели на достоинства и недостатки основных стратегий прогнозирования.
Протестировали на некотором датасете стратегии, которые реализованы в ETNA, и увидели улучшение метрики качества после их применения.
Если вы хотите предложить новую фичу, задать вопрос или порекомендовать тему для статьи, ждем в нашем GitHub — там все контакты. Там же можно и поставить звездочку, если материал вам понравился.
На прощание — пара полезных статей для тех, кто хочет узнать больше:
Bontempi G., Ben Taieb S., Borgne Y. A. L. Machine learning strategies for time series forecasting //European business intelligence summer school — Springer, Berlin, Heidelberg, 2012
Taieb S. B. et al. A review and comparison of strategies for multi-step ahead time series forecasting based on the NN5 forecasting competition //Expert systems with applications — 2012. — Т. 39. — №. 8
