
В прошлой статье мы разобрали идею нашего компонентного анализатора и поделились результатами некоторых экспериментов, проведенных в лабораторных условиях. Результаты, полученные на маленькой части датасета в размере 3000 библиотек, вышли довольно оптимистичными. В этой статье опишем сложности, с которыми мы столкнулись при попытках применить решение на ~105к библиотек, и расскажем, как с ними справлялись.
Первые попытки масштабировать решение
После проведенных экспериментов у нас было все, чтобы раскатиться на большее число библиотек. В итоге мы получили датасет на 25 млн векторов размерности 768. Объем таких данных без сжатия — около 71 ГБ, и потенциально объем данных после построения индекса увеличится.
Обозначим одну малоприятную деталь: для поиска ближайших векторов в Milvus весь датасет с индексом должен быть загружен в оперативную память. У нас не было таких ресурсов, поэтому мы решили использовать DiskANN — свежий алгоритм, который позволяет делать поиск по данным на NVMe-дисках. Он строит на точках датасета взвешенный граф и на запрос ходит по ребрам графа, приближая искомую точку.
Индекс DiskANN оказался очень прожорлив по ресурсам: на наш датасет 200 ГБ памяти оказались нижней границей. Кроме того, мы столкнулись со сложностями при построении индекса, которые решились переходом на новую версию Milvus, вышедшую буквально на днях.

В итоге точность получилась околонулевой: мы протестировали модель на jar-файле, собранном из зависимостей датасета. Сначала оказалось, что у индекса вышел плохой recall, мы быстро поправили это подгоном гиперпараметров и обнаружили другую проблему: в базе слишком много повторяющихся векторов.
Частой оказалась ситуация, в которой какой-то класс библиотеки настолько типичен, что встречается более чем в 500 других библиотеках. Эта проблема была и в экспериментах из прошлой статьи, но там она решалась эвристиками поиска: на запрос в милвус мы искали 30 ближайших и группировали по расстоянию, этого оказывалось достаточно, чтобы выяснить, встречается ли метод в разных библиотеках. На большом датасете наш метод оказался несостоятельным.
Кроме того, для работы модели необходима GPU, поскольку мы используем тяжелый трансформер RoBERTa и даже так обработка тестового jar-ника на ~4к классов занимала около 15 минут. Мы обозначили две дальнейшие стратегические цели: избавиться от повторов векторов в базе и перейти на более легкую модель, в идеале — с возможностью инференса на CPU.
Переход на более легкую языковую модель
Мы остановились на all-MiniLM-L6-v2 в силу ее легкости и хороших показателей качества в сравнении с другими моделями. Мы протестировали all-MiniLM-L6-v2 в условиях первых экспериментов на маленьком датасете:
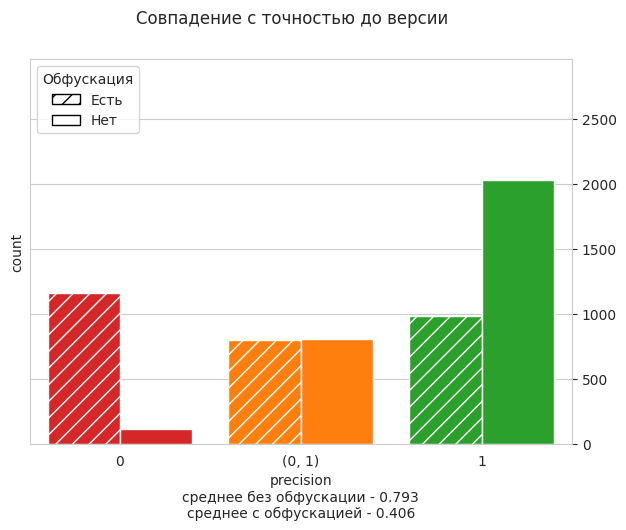
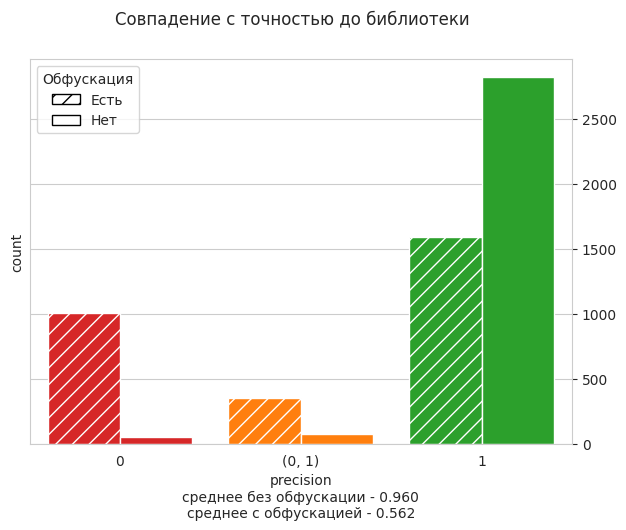
По сравнению с RoBERTa качество просело только при обфускации, но мы готовы пойти это в пользу лучшего быстродействия. Мы использовали перевод модели в формат ONNX и на 6-ядерном 2,6 GHz.
В итоге обработка тестового jar-ника с ~4к классами стала занимать в среднем 11 минут. Размерность эмбеддингов здесь — 384, так что это потенциально уменьшает в два раза затраты на хранение данных.
Удаление повторов векторов в базе
В случае с повторами не удалось легко найти готовое решение или алгоритм. Из-за особенностей milvus избавиться от дубликатов в существующей базе сложнее, чем просто завести новую базу и поддерживать в ней отсутствие повторов.
Сложность заключается в том, что самый прямолинейный алгоритм с линейным поиском по базе данных будет занимать квадратичное время от количества классов во всех библиотеках: чтобы убедиться, что вектор не дубликат какого-то, нужно делать запрос в базу данных. В нашем случае для 25 млн объектов это непозволительно долго, то есть без индекса не обойтись. Но индекс не гарантирует 100% recall поиска, точность сильно зависит от гиперпараметров. Тогда можно строить и обновлять индекс на векторах прямо на ходу, поддерживая гиперпараметры для оптимальной точности и быстроты поиска.
Способ хранения данных показал свою несостоятельность: для каждого вектора информация о том, из какой библиотеки он пришел, хранилась в milvus рядом с вектором, а это не очень удобно.
Мы решили завести отношение в Postgress базе данных, где для каждой библиотеки будем хранить индексы векторов в milvus. В итоге алгоритм такой:
Заводим пустой датасет без индекса.
Считаем векторы классов библиотек и пытаемся добавить их в базу, перед добавлением проверяя, что их уже нет:
оптимальнее набирать некоторый батч векторов и отдавать его в milvus для поиска ближайших;
среди тех векторов, которые не нашлись, выделить уникальные, ведь в пределах одного батча могут быть повторы;
добавить в базу уникальные векторы, вернув их индексы;
с предыдущих шагов для всех векторов батча мы получили индексы их векторов — осталось занести эту информацию в Postgress отношение.
При достижении некоторого размера датасета строим на нем индекс IVF_FLAT с оптимальными гиперпараметрами.
Продолжаем обновлять базу векторов, повторяя шаг 2 и перестраивая индекс для поддержания оптимальных гиперпараметров.
Параметры индекса подбирали на основе статьи из блога milvus. Мы взяли IVF_FLAT потому что алгоритм основывается на разделении всего датасета на nlist кластеров, и поиск происходит сначала по центрам кластеров, а затем линейно внутри nprobe ближайших кластеров. Индекс не требует дополнительной памяти, время построения зависит от алгоритма кластеризации, но в milvus используется эвристический K-means Ллойда, обеспечивающий линейную асимптотику.
Алгоритм отработал за 1,5 дня, и датасет получился в 2,64 млн векторов. Параллельно мы решили еще и проблему с объемом данных: теперь векторы с лихвой умещаются в 16 ГБ оперативной памяти. У нас сразу возникла мысль о том, что можно перейти к более мелкому разбиению: использовать вместо классов векторы методов.
Модели-трансформеры имеют ограничение в 512 токенов на длину входной последовательности. Когда мы считали эмбеддинги классов, брали mean-pooling эмбеддингов методов. При более мелком разбиении можем позволить себе не терять информацию при взятии среднего, а сразу брать эмбеддинги методов в базу. Мы посчитали датасет векторов для методов — вышло 4,93 млн элементов, а подсчет занял уже 5 дней. Все тесты мы проводили с использованием методов.
Тесты, проблемы и немного читерства
Мы договорились решать проблемы по мере их поступления и на время забыли про обфускацию, а все тесты проводили с n_neigbours=1.
Для начала проверили на тестовом jar-файле: из 21 зависимости нашли 19, при этом выдали 500 false-positive. Двух зависимостей, которые модель не увидела, не было в датасете. При более детальном рассмотрении оказалось, что большинство fp — пакеты, у которых множество методов в исходном коде ограничивается одним, двумя или тремя представителями. Если их убрать, выйдет 15 истинных зависимостей и 41 fp. Причем 35 пакетов из этих 41 — неправильные версии библиотек из зависимости.
Мы столкнулись с проблемой: есть некоторое множество библиотек, которые в рамках нашего метода могут являться причиной значительного количества fp, ведь в них мало методов и эти методы встречаются где-то еще, но даже если их убрать, получается много ошибок в версиях.
Мы придумали способ, который не выкинет из рассмотрения проблемные библиотеки, но будет использовать дополнительную информацию в виде констант. Есть другой путь — работать в допущении, что такие пакеты нас не сильно интересуют и их можно убрать из датасета путем фильтрации по векторам. Его мы рассмотрим далее.
Метод с константами гарантирует нам 100% recall, но вот precision под вопросом. Тогда мы решили сделать так:
взять для каждой библиотеки не все константы, а малую часть — 500 штук;
завести pg-отношение, в котором сохранить, из какой библиотеки пришла константа;
пересечь предсказание бейзлайна с предсказанием нашей модели, чтобы лишние мелкие библиотеки отсеялись.
Да, это выглядит как читерство, но если у большинства файлов, которые мы наблюдаем, есть такая замечательная особенность, то почему бы ею не воспользоваться? Тем более решение обошлось нам бесплатно: бейзлайн уже реализован, а за счет ограничения на число констант мы получили маленькое отношение в pg и быстрые запросы. Но результаты вновь разочаровали: вышло 19 tp и 34 fp, все из них — неправильные версии истинных зависимостей.
Мы не собирались сдаваться и руками разобрали все fp-случаи. Оказалось, что они неотличимы по коду от истинной версии в зависимости. Вот пример библиотеки google-http-client-apache-v2-1.42.0. В предсказании выдается 15 ее версий (кроме них в датасете есть еще одна версия — 1.33.0):
1.34.0 | 1.38.0 | 1.38.1 | 1.39.0 | 1.39.2 |
1.40.1 | 1.41.0 | 1.41.1 | 1.41.4 | 1.41.7 |
1.41.8 | 1.42.0 | 1.42.2 | 1.42.3 | 1.43.1 |
Если на официальном репозитории рассмотреть разницу между 1.34.0 и 1.43.1, то в папке google-http-client-apache-v2 нет существенных семантических изменений в сурс-коде: комменты, новые поля в методах.
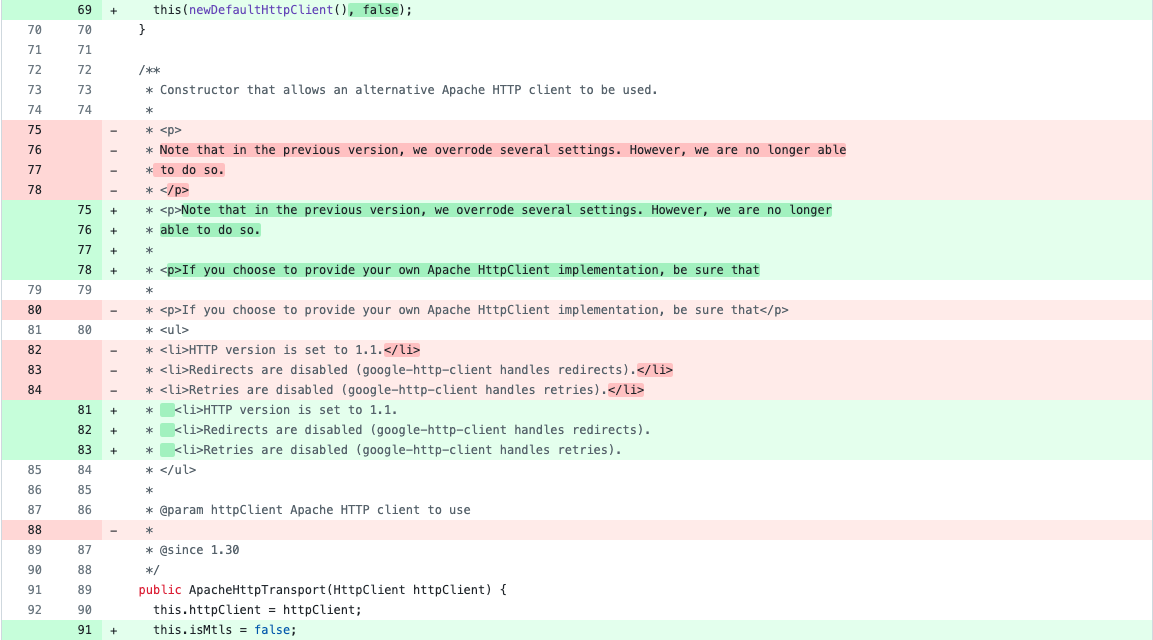
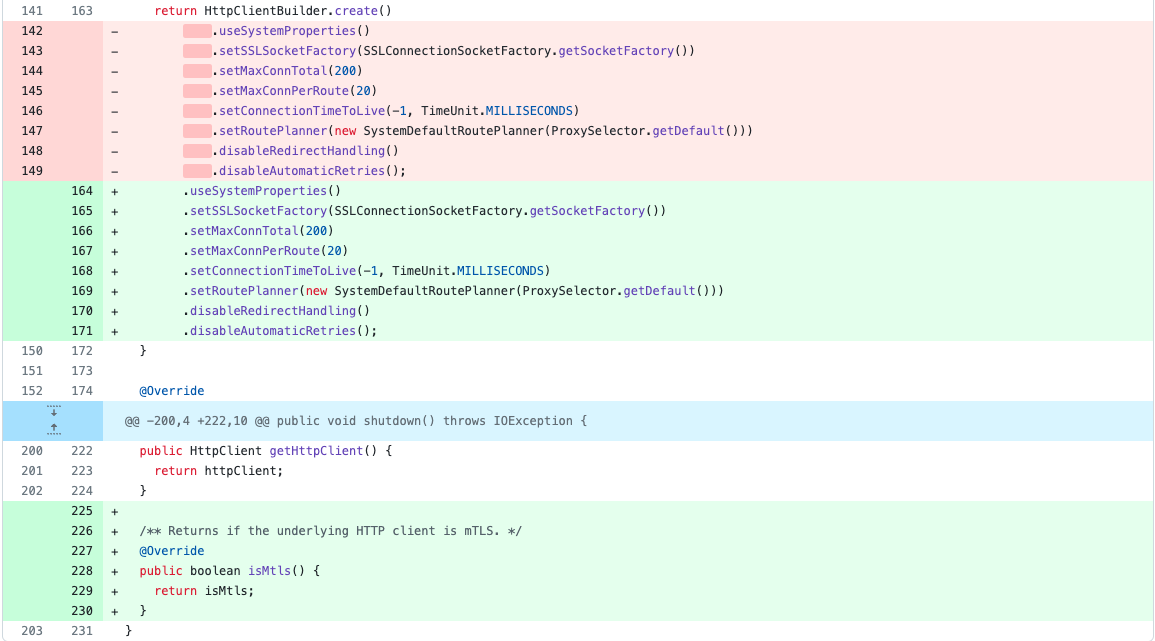
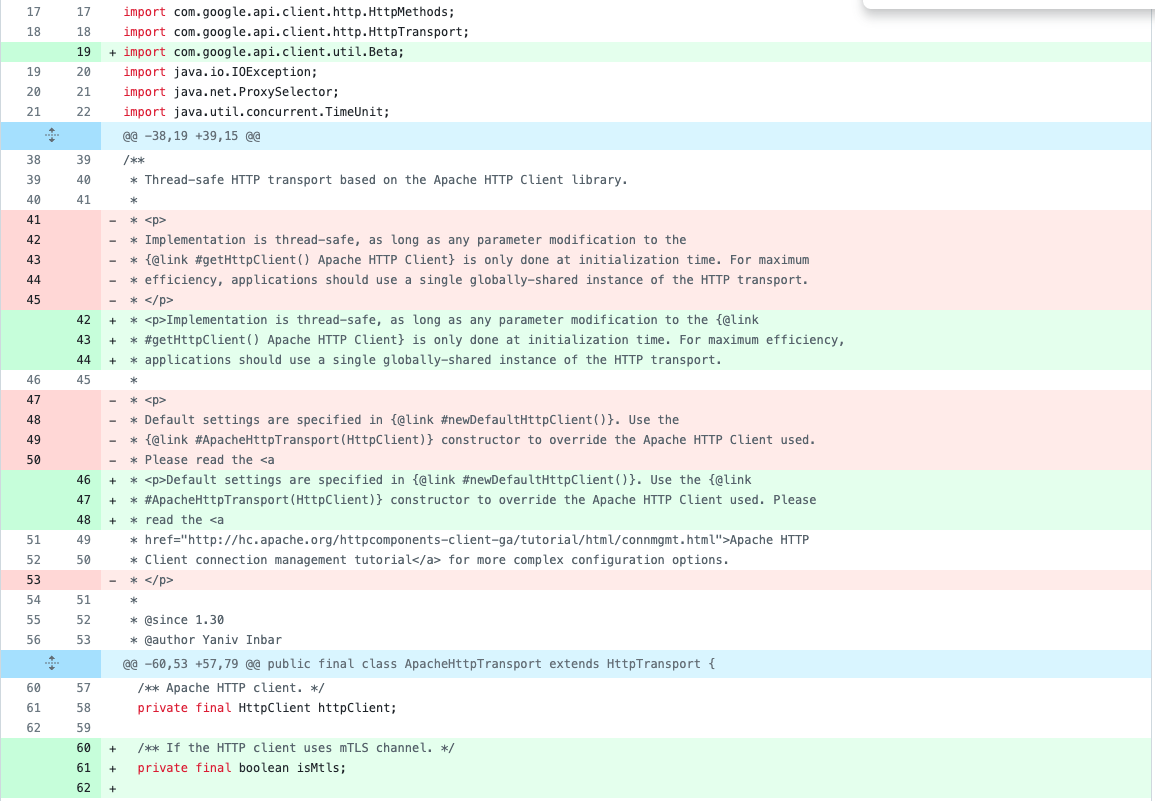
Аналогично вышло с остальными зависимостями. У нас возникла гипотеза: различные версии библиотеки, выдаваемые в предсказании, в действительности будут неразличимы по коду. В том смысле, что множество их классов и методов совпадает, как и соответствующий им байт-код.
Проверка гипотезы с одинаковым кодом
Для проверки гипотезы о различных версиях библиотек мы изменили подход к эксперименту. До этого мы давали на вход модели одну библиотеку и ожидали ее на выходе, теперь же приблизили эксперимент к более реальным условиям. Мы давали модели на вход jar-файлы, собранные из произвольных библиотек датасета, и ждали на выходе именно эти библиотеки.
Мы зафиксировали датасет из 1000 jar-файлов, каждый из которых содержит 4—15 зависимостей. Метрики считали поэлементно, то есть для каждого jar-файла:

В базовом варианте мы смотрели на имена библиотек и версий, то есть считали за ошибки любое несовпадение по имени или версии библиотеки. Важно было учесть, что код различных версий может совпадать. Мы решили, что если fp-случай был ошибкой в библиотеке, а значит, никакой другой версии пакета нет в зависимостях, то считать это за fp. Во всех других случаях — это ошибка в версии пакета из зависимостей, мы сравниваем байт-код лишней версии с истинной и, если он отличается, считаем это за fp-случай.
Мы смогли сравнить, как много встречается неоправданных fp-случаев: когда формально по имени это fp, но на самом деле это неотличимая версия какой-то библиотеки из зависимости. Нет ничего плохого в таких случаях, ведь в конечном итоге полученный SBOM будет использоваться для конкретных задач, например анализ CVE.



Можно сказать, что гипотеза про неразличимые по коду fp подтвердилась: видим значительный прирост в метрике, если не учитывать совпадающий код как ошибку. Получается, что только 1204 fp-версий из 35 081 отличаются от истинной версии по коду. Но нужно не забывать про случаи, когда fp — не иная версия какой-то истинной зависимости. Из-за таких все еще есть ошибки по коду в 416 элементах датасета, то есть, несмотря на то что в пределах одного элемента датасета в среднем ошибаемся не сильно, ошибаемся довольно часто в общем.
Две крайности: только константы или только векторы
В следующем эксперименте мы использовали только константы:

Пример показывает, как сильно использование при анализе информации о коде повышает точность определения зависимостей
Еще один эксперимент был посвящен тому, можно ли использовать только векторы, ведь до начала эксперимента мы ставили цель быть устойчивыми к обфускации, а теперь используем константы.
При использовании только векторов в предсказании появляется много мелких библиотек, методы которых не являются репрезентативными. Из отношения в Postgres мы с легкостью можем получить распределение числа библиотек, к которым относится вектор:
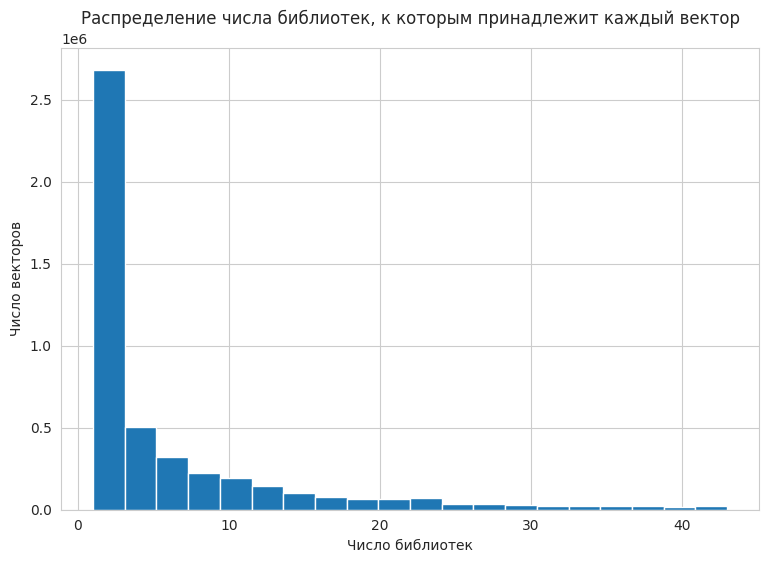
Сразу возникает простая идея: давайте не учитывать в анализе векторы, которые встречаются хотя бы в X пакетах. В каком-то смысле X отвечает за контроль recall: чем оно меньше, тем меньше библиотек датасета мы сможем потенциально распознать. Иначе говоря, мы теряем какие-то библиотеки из рассмотрения (уменьшение recall), но те библиотеки, которые остаются, лучше различимы между собой, поэтому уверенность в правильности больше и больше precision.
Возникает вопрос: сколько библиотек мы потенциально теряем при разных значениях X?
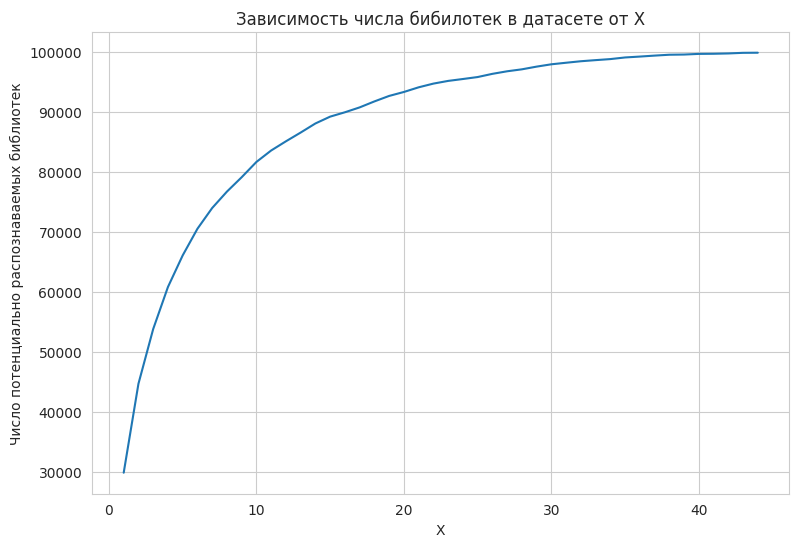
При X = 40 мы теряем около 5000 библиотек. Если мы хотим precision = 1, можно взять X = 1, правда, при этом сможем потенциально распознать лишь треть датасета. Но можно ли добиться trade off путем подбора оптимального X? Взглянем на метрики при X = 40:


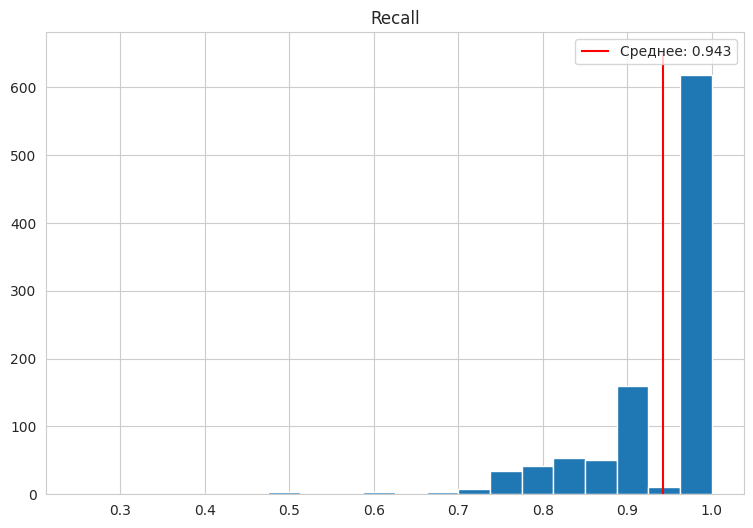
Вышло заметно хуже, чем при использовании векторов с константами, но лучше, чем только константы. Теперь попробуем X = 10:

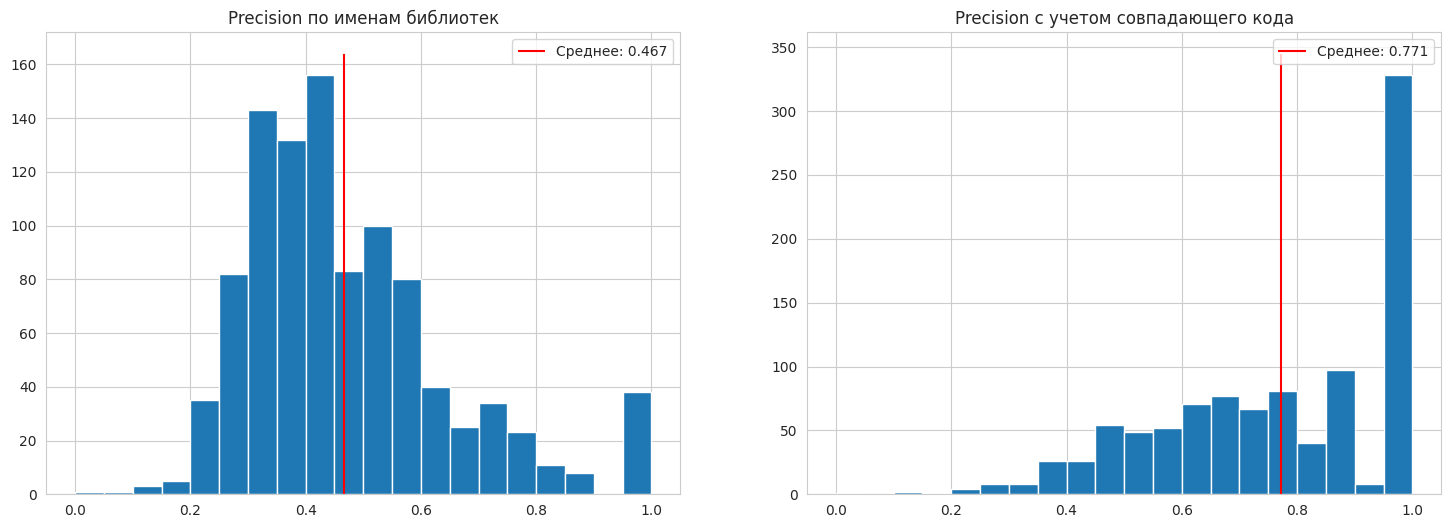

На самом деле можно отсеивать векторы не только по числу пакетов, в которых они представлены. Можно пробовать разные статистики векторов: считать число пакетов с точностью до имени библиотеки, игнорируя версии (например, эмбеддинг встречается в трех версиях библиотеки A и в десяти версиях библиотеки B, тогда значение статистики — 2). Или считать библиотеки не для конкретного вектора, а для какой-то его окрестности.
Какие выводы мы сделали
К сожалению, мы не успели оценить качество модели на обфусцированных данных. Время на задачу вышло, а мы его потратили слишком много, чтобы заставить модель внятно работать на большом датасете и понять причину большого числа FP.
Но и тот опыт, что мы успели получить, считаем достаточно ценным. К примеру, повторы векторов в базе — зло, которое мешает модели работать, и мы нашли способ избавиться от них за приемлемое время.
Смотреть только на имена пакетов при подсчете метрик — гиблая затея, ведь выяснилось, что бывает куча неразличимых по коду версий. Кроме того, этот подход никак не завязан на jar-файлах: единственная их особенность, которой мы пользовались, — большое число информации в константах.
Но, как выяснили в последнем пункте, добиться вменяемой точности можно за счет качественного отбора векторов. В целом можно переложить подход на другие бинарные файлы, в качестве дизасемблера использовать тот же rizin, за единицу разбиения брать функции или компоненту связности в графе вызовов — далее все абсолютно аналогично.
На этом наша стажировка закончилась и мы перешли в штат — решать еще более интересные задачки. Но это уже совсем другая история.
