Comments 11
Отличная статья, действительно надо нести в массы знание о том, что подход когда из выборки выкинем верхние и нижние 2% значений и потом натянем на это гаусса не всегда валиден и позволяет пропустить важные вещи. Но удивлён что здесь не присутствует ссылка на книгу Талеба "Статистические последствия жирных хвостов" которая вся об этом.
С финансовыми рынками и корелляцией и без индексов можно заметить такие моменты когда резко все начинают двигаться в одну сторону.
У меня была забавная история - в 2017 я пытался найти корелляцию между разными криптовалютами. Заметил что в одни дни одни растут, а другие падают, а потом они меняются местами. Возникла теория что если откупать самые упавшие и продавать те что в топе дня - можно было бы заработать. Экспортировал данные по 70 валютам что торговались на одной известной тогда бирже и загнал в табличку в Numbers. Изменения в процентах за день. К сожалению, такое количество данных тормозило график. И я решил всё это дело распечатать и склеить рулоном с помощью скотча. Увы, но график получился слишком большим чтобы поместиться раскатанным на полу, потому я обвесил второй этаж дома по кругу графиком, обклеив в том числе и шкафы. И так уже влезло.
И да, действительно - посмотришь на график - равной полосой идет - где-то выросло, где-то упало. Но были моменты когда график резко двигался вверх или вниз - в те дни сразу все валюты, почти без исключений, двигались в одну из сторон. А потом распределение возвращалось.
В конце концов, преподаватель по статистике сказал, что практически всё можно описать с помощью распределения Гаусса
Плохой преподаватель. Посоветуйте ему почитать, например, Мандельброта, Леви или Талеба.
Поэтому настоящие «толстые хвосты», которые мы видим в реальном мире — это нечто более коварное, чем то, что описывается простыми распределениями Коши или Парето. Они, некоторое время, может — годы или десятилетия, могут вести себя как распределения Гаусса.
Просто неверно. Вы думаете что кроме Коши и Парето ничего нет. Есть целый класс L-устойчивых распределений (как раз с тяжелыми хвостами), которые при определенных параметрах вообще не будут похожи на нормальное распределение. То что вы описываете ("похоже на гаусса") - это частный случай, будет например когда L-устойчивого распределения близко к 2. (Например 1,999). Нормальное распределение или распределение Гаусса - это частный случай устойчивого при
. Распределение Коши - частный случай, когда
.
Более того, то что происходит в котировках на бирже, гидрологии при разливе рек или в распределении воздействия масс космических тел (Хольцмарка) - это точно не похоже на Гаусса и это заметно даже без внушительной базы наблюдений. Опять же читайте Мандельброта, он рассматривает эти не мифические, а реальные примеры.
Выражения типа "могут вести себя как распределения Гаусса" это очень опасная вещь, Если скажем вы возьмете смесь (mixture) двух гауссовых распределений 99% c очень маленкой и 1% с очень большой
то вы можете ошибочно посчитать в ходе эмпирических наблюдений что есть выбросы за пределы ваших неверно оцененных 3 сигм очень часто и посчитать, что там есть толстые хвосты, хотя их нет и быть не может. Вообще, конечно, очень опасно утверждать что какой-то там процесс в природе точно описывается нашей мат. моделью, но утверждать что толстые хвосты распределений - это странно как у вас в заголовке я бы не стал. Странно и загадочно то, откуда они берутся и в каких условиях и в каких процессах их следует ожидать, а в каких нет, чтобы строить адекватные модели.
Меня в последнее время все больше интересует почему некоторые статьи плохие, а некоторые хорошие, почему одни ""заплюсовываются", а другие нет. Это я вовсе не к тому, что плюсы накручены, а к тому, что есть какая-то проблема рефлексии во всей этой научной деятельности. Какое-то странное стремление все упрощать.
Смотрите, устойчивые распределения известны давно. Если мне не изменяет память, то открыл их Леви еще в начале XX-го. Кстати в scipy.stats по моему даже есть распределение Леви. Есть куча книг и работ по их приложениям в разных науках. Включая биржи.
Если сделать в нормальном распределении матожидание и дисперсию зависимыми от времени, и сэмплировать из такого генератора значения, то мы тоже получим длинные хвосты. Техники давно заметили, что именно так и происходит износ механизмов.
Чуваки, которые занимаются теорией самоорганизации, говорят что наличие длинных хвостов свидетельствует о наличии внутренней динамики систем, подчиняющейся определенным правилам. Марковские и байесовские сети, к примеру, могут восстановить такие правила.
В управлении рисками - степень игнорирования длинных хвостов (выбросов), определяет степень склонности к риску.
Все это давно известно. Но почему статья так "залайкана"? Откуда такой интерес к длинным хвостам? В последнее время, мне лично стало как-то прикольно выдвигать гипотезы о причинах. Дело может быть в банальной подаче материала. В репутации компании и автора (в конце концов материал ведь переводной и не совсем исчерпывающий). А может быть это так себя проявляет метамодерн :)
Но как бы там ни было, это хороший интерес. Спасибо за статью (предыдущие статьи тоже). Плюсую обеими руками!
Людям нравится узнавать новое. Причём не просто новое, а "захватывающее" новое.
О "толстые хвостах" говорят очень редко вне узкого круга специалистов. И при этом они ломают шаблоны заложенные упрощённым теорвером из школы и первого курса института. Это необычно, и захватывающе, и научно. и кажется, что полезно!
Потому и плюсуют.
+45 это разве залайкана?
Но объективно, автор очень хорошо поймал баланс доступности материала - с одной стороны понятно даже тем, кто уже забыл матстат. С другой - уровень значительно выше базовой жвачки для совсем новичков.
Если сделать в нормальном распределении матожидание и дисперсию зависимыми от времени, и сэмплировать из такого генератора значения, то мы тоже получим длинные хвосты. Техники давно заметили, что именно так и происходит износ механизмов.
Не очень понял что вы имеете ввиду. То, что вы описываете это просто похоже на нестационарный случайный процесс. Каким образом должны зависеть матожидание и дисперсия этого генератора от времени, чтобы при наблюдениях получились хвосты как вы говорите? Дело же не просто в длинных хвостах, а в толстых (тяжелых) хвостах, которые убывают как правило по степенному закону.
Имеется ввиду, что если мы просчитываем нестационарный процесс как стационарный (т.е. без учёта времени - просто все данные зальём в гистограмму без разбора) - то получим "толстые хвосты".
И это можно использовать (и используют) для детектирования того, что у нас процесс "поплыл".
Т.е. если хвосты "тонкие", экспоненциальные - то всё хорошо, процесс центрирован и никуда не движется. Хвосты "потолстели" - значит что-то там износилось, пора посылать наладчиков разбираться.
import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt
import seaborn as sns
samples = []
mu, sigma = 0, 1
for i in range(100):
samples.append(norm.rvs(mu, sigma, size=100))
mu += 1
sigma += .5
sns.kdeplot(np.hstack(samples));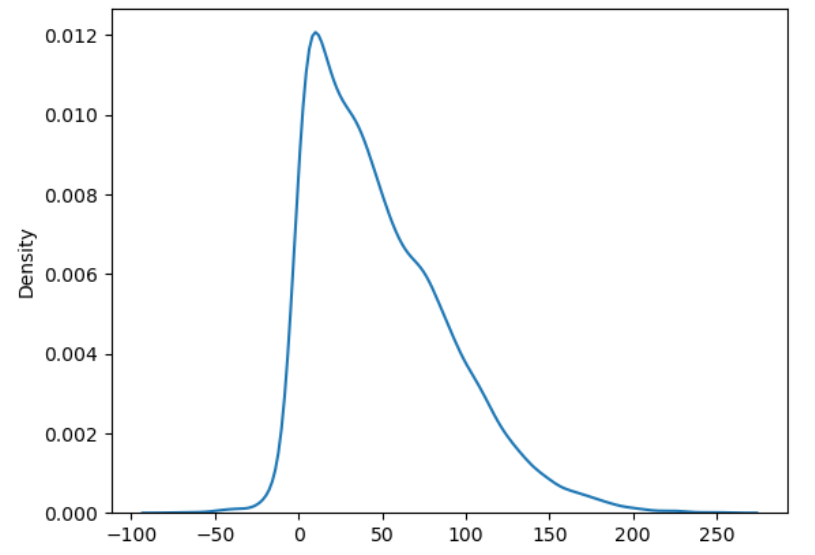
Если проследить за вибрациями например какого-нибудь подшипника, то они будут выглядеть именно так. Но если их смотреть в каждый отдельный день, то их поведение будет нормальным.
Толстые хвосты распределений — это загадочно и странно