Comments 31
Первый курс любого технического факультета?
Меня беспокоит формулировка «отель с бесконечным количеством номеров. Все номера в отеле уже заселены»
Слово «Все» обычно относится к конечному количеству чего-либо. Тоесть например в корзине 100 шариков и все они белые.
Я еще могу представить себе бесконечное количество номеров, как что-то всё время увеличивающееся, тоесть вот вереница номеров, она стремится в бесконечность и каждый момнет времени появляются всё новые и новые номера, но все они заняты.
Или даже я вижу не первую комнату этой вереницы, а просто вереницу комнат, которая уходит от меня в бесконечность в обе стороны, и может быть даже где-то в бесконечно удаленной точке концы этой вереницы замыкаются, не важно
Но в ообоих случаях новым постояльцам не найдется места, потому что Все номера заняты :)
Слово «Все» обычно относится к конечному количеству чего-либо. Тоесть например в корзине 100 шариков и все они белые.
Я еще могу представить себе бесконечное количество номеров, как что-то всё время увеличивающееся, тоесть вот вереница номеров, она стремится в бесконечность и каждый момнет времени появляются всё новые и новые номера, но все они заняты.
Или даже я вижу не первую комнату этой вереницы, а просто вереницу комнат, которая уходит от меня в бесконечность в обе стороны, и может быть даже где-то в бесконечно удаленной точке концы этой вереницы замыкаются, не важно
Но в ообоих случаях новым постояльцам не найдется места, потому что Все номера заняты :)
> Слово «Все» обычно относится к конечному количеству чего-либо. Тоесть например в корзине 100 шариков и все они белые.
Слово «все» относится к любому количеству чего-либо. Например: «Натуральных чисел бесконечно много и все они раскладываются на простые множители». Обратите внимание: их уже бесконечно много, а не появляются всё новые и новые. Различие между потенциальной и актуальной бесконечностью штука тонкая.
Слово «все» относится к любому количеству чего-либо. Например: «Натуральных чисел бесконечно много и все они раскладываются на простые множители». Обратите внимание: их уже бесконечно много, а не появляются всё новые и новые. Различие между потенциальной и актуальной бесконечностью штука тонкая.
Слово «Все» обычно относится к конечному количеству чего-либо.Все натуральные числа делятся на 1. Все натуральные числа либо простые, либо составные, кроме единицы. Все номера заняты постояльцами. Не вижу проблемы.
qrazydraqon, AraneusAdoro
Замечательно
А теперь применим к вашим тезисам начало статьи :)
«Натуральных чисел бесконечно много и все они раскладываются на простые множители»
А тут прихожу я (ну типа новый постоялец) и говорю: а подайте-ка мне натуральное число, которое не раскладывается на простые множители, я его сам разложу (т.е. займу пустой номер)
Или вот «Все натуральные числа делятся на 1» — а мне нужно число которое входит в состав этого бесконечного множества натуральных чисел, но не делится на 1
Слово «Все» наверное является причиной парадокса
Замечательно
А теперь применим к вашим тезисам начало статьи :)
«Натуральных чисел бесконечно много и все они раскладываются на простые множители»
А тут прихожу я (ну типа новый постоялец) и говорю: а подайте-ка мне натуральное число, которое не раскладывается на простые множители, я его сам разложу (т.е. займу пустой номер)
Или вот «Все натуральные числа делятся на 1» — а мне нужно число которое входит в состав этого бесконечного множества натуральных чисел, но не делится на 1
Слово «Все» наверное является причиной парадокса
Нет. «Занят» — изменяемое свойство, номер можно и освободить. В отличие от указанных в комментариях. Заняты-то все, но поскольку их бесконечно много, можно без ущебра для постояльцев освободить любое количество номеров (хоть бесконечное).
Парадокса тут нет, btw.
Парадокса тут нет, btw.
Поясните, что значит свойство «изменяемое» и «неизменяемое». Вы задали свойство для всех элементов. В чем разница с примерами выше?
Такое ощущение, что вы пытаетесь дать правильное определение через неуместные примеры, какой-то читинг.
Такое ощущение, что вы пытаетесь дать правильное определение через неуместные примеры, какой-то читинг.
Другими словами, я могу вас попросить обосновать — почему такой сдвиг возможен?
В по моим «интуитивным» аксиомам, он не возможен, так как если бы мы захотели сдвинуть — мы уперлись бы в занятый номер. Продолжая дальше, мы бы так и не смогли отыскать свободный — двигаясь бесконечно в сторону увеличения номера комнаты.
Я не к тому, что Гильберт был неправ :), а к тому, что такие интуитивные примеры опасны. Интуиция у всех по разному работает.
В по моим «интуитивным» аксиомам, он не возможен, так как если бы мы захотели сдвинуть — мы уперлись бы в занятый номер. Продолжая дальше, мы бы так и не смогли отыскать свободный — двигаясь бесконечно в сторону увеличения номера комнаты.
Я не к тому, что Гильберт был неправ :), а к тому, что такие интуитивные примеры опасны. Интуиция у всех по разному работает.
Можно попробовать представить это так: по системе оповещения отправляем сообщение «Всем переселиться в следующий номер», и все одновременно переселяются. Если новых постояльцев бесконечное число — «Всем переселиться в номер 2n»; освободится бесконечное число номеров.
Как-то неконструктивно :)
Серьезно, для кого-то это может показаться логичным объяснением. Для меня не работает. Ну совсем неинтуитивно. Может, честнее ввести аксиомы и дать несколько примеров, чтобы показать что это действительно удобно и работает?
В чем разница между параллельной рассылкой и последовательным вытеснением? Почему в одном случае работает, в другом нет, ведь по сути тож самое. Далее могу спросить, что такое бесконечность, как мы ее определяем. Можем ли мы послать сообщение одновременно всем жильцам и т.п.
Серьезно, для кого-то это может показаться логичным объяснением. Для меня не работает. Ну совсем неинтуитивно. Может, честнее ввести аксиомы и дать несколько примеров, чтобы показать что это действительно удобно и работает?
В чем разница между параллельной рассылкой и последовательным вытеснением? Почему в одном случае работает, в другом нет, ведь по сути тож самое. Далее могу спросить, что такое бесконечность, как мы ее определяем. Можем ли мы послать сообщение одновременно всем жильцам и т.п.
Вы пытаетесь смотреть на этот вопрос, как на вопрос о чем-то реальном и физическом. Ну, успехов в поисках отеля с бесконечным числом номеров.
Речь же не о пракической вещи, а о том, что для бесконечных множеств часть не обязательно меньше целого (в отличие от конечных).
Строго же говорится вот о чем: для конечных множств есть принцип Дирихле. Говорит он о том, что для конечных множеств одинакового размера и отображения между ними эквивалентно: 1) отображение инъективно (никакие два элемента не переходят в один и тот же) и 2) отображение сюръективно (в любой элемент что-нибудь переходит).
Для отображения множества натуральных чисел в себя разница между инъективностью и сюръективностью есть: отправьте каждое число n в число n+k для некоторого фиксированного k — инъективность есть, но есть k чисел, в которые ничего не переходит при таком отображении (это и есть освободившиеся номера отеля).
Но вообще разница может быть огромной: отправьте каждое n в 2n, и ни в какое нечетное число ничего не перейдет (освободится счетное число номеров).
Речь же не о пракической вещи, а о том, что для бесконечных множеств часть не обязательно меньше целого (в отличие от конечных).
Строго же говорится вот о чем: для конечных множств есть принцип Дирихле. Говорит он о том, что для конечных множеств одинакового размера и отображения между ними эквивалентно: 1) отображение инъективно (никакие два элемента не переходят в один и тот же) и 2) отображение сюръективно (в любой элемент что-нибудь переходит).
Для отображения множества натуральных чисел в себя разница между инъективностью и сюръективностью есть: отправьте каждое число n в число n+k для некоторого фиксированного k — инъективность есть, но есть k чисел, в которые ничего не переходит при таком отображении (это и есть освободившиеся номера отеля).
Но вообще разница может быть огромной: отправьте каждое n в 2n, и ни в какое нечетное число ничего не перейдет (освободится счетное число номеров).
Да не пытаюсь я представить реальный бесконечный отель. Я просто пытаюсь понять, зачем нужно приводить эту аналогию. Когда-то давно мне ее уже приводили. Ничего не понял, начал спрашивать. Не ответили внятно… Так зачем эта аналогия? Просто потому что ее привел Гильберт? Или я туплю… не знаю.
Ладно, если это кому-то помогает, вопросы снимаю. На счет принципа дирихле — странная формулировка. Обычно говорится что невозможно построить инъекцию во множество меньшей мощности. Ну да ладно, аргумент я понял.
зы ушел читать ZFC
Ладно, если это кому-то помогает, вопросы снимаю. На счет принципа дирихле — странная формулировка. Обычно говорится что невозможно построить инъекцию во множество меньшей мощности. Ну да ладно, аргумент я понял.
зы ушел читать ZFC
Здесь рассматриваются различные множества чисел и некоторые свойства их, к которым люди изучающие математику обращаются вновь и вновь на протяжении всей жизни, говорить об этом как об материале первого курса не стоит, а тем кому тема станет интересна еще советую обратиться к трудам Георга Кантора
Может кто-то не видел, интересная тема для дискуссии:
Невероятно! 1 + 2 + 3 + 4 + 5 + ... = -1/12
Вообще-то мне действительно хотелось обсудить этот момент. Мне тоже показалось, что это какой-то развод, но похоже этим занимаются серьёзные дядьки, на википедии есть статья.
PS: ладно коммент не понравился, но вы ж меня так в ro загоните
PS: ладно коммент не понравился, но вы ж меня так в ro загоните
Никакой это не развод, просто всё зависит от определений. Конечно, в обычном смыле этот ряд расходится, его сумма равна плюс бесконечности. Однако, если путём аналитического продолжения продолжить дзета-функцию Римана и там воспользоваться (по аналогии) её разложением в ряд (который, конечно, расходится вне своего круга сходимости), то получится как раз приведённое вами равенство. То есть, это никак не сумма в обычном понимании, просто получается удобно в некоторых областях физики (и не только) пользоваться таким представлением.
Кстати, доказательство в этом видео (и в других подобных тоже) математически неверно. С не-абсолютно-сходящимися рядами нельзя так просто брать и производить перестановки членов, например. Есть даже теорема, что из условно сходящегося ряда путём перестановки его членов можно получить любое (!) число.
Кстати, доказательство в этом видео (и в других подобных тоже) математически неверно. С не-абсолютно-сходящимися рядами нельзя так просто брать и производить перестановки членов, например. Есть даже теорема, что из условно сходящегося ряда путём перестановки его членов можно получить любое (!) число.
Спасибо за ответ, я тоже пришёл к выводу, что переставлять или сдвигать элементы в последовательности нельзя.
Но если это математически не верно, то какая из этого может быть практическая польза? Может быть вы знаете где это используется?
Но если это математически не верно, то какая из этого может быть практическая польза? Может быть вы знаете где это используется?
В этой области я совсем не специалист, с реальным использованием таких и подобных рядов не сталкивался, поэтому далее лишь моё предположение.
Присвоение сумме такого ряда значения 1/12 производится путём регуляризации дзета функции, которая представима рядом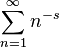
в его круге сходимости. Дзета функцию, как обычную функцию, можно аналитически продолжить в частности в точку s=-1. Несмотря на то, что вообще говоря ряд в этой точке не сходится (он как раз равен 1+2+3+...), ему логично присвоить именно значение дзета функции при s=-1.
Кстати, есть ведь куча других методов суммирования различных расходящихся рядов. Самый известный, простой, интуитивно понятный — пожалуй, суммирование по Чезаро. По сути, он тоже использует идею логичного и согласованного с другими результатами присвоения конкретных значений суммам рядов. То же самое и с рядом 1+2+3+… — но он не суммируем и по Чезаро, поэтому понадобился ещё один метод (аналитическое продолжение).
Присвоение сумме такого ряда значения 1/12 производится путём регуляризации дзета функции, которая представима рядом
в его круге сходимости. Дзета функцию, как обычную функцию, можно аналитически продолжить в частности в точку s=-1. Несмотря на то, что вообще говоря ряд в этой точке не сходится (он как раз равен 1+2+3+...), ему логично присвоить именно значение дзета функции при s=-1.Кстати, есть ведь куча других методов суммирования различных расходящихся рядов. Самый известный, простой, интуитивно понятный — пожалуй, суммирование по Чезаро. По сути, он тоже использует идею логичного и согласованного с другими результатами присвоения конкретных значений суммам рядов. То же самое и с рядом 1+2+3+… — но он не суммируем и по Чезаро, поэтому понадобился ещё один метод (аналитическое продолжение).
В отличие от окружающего нас мира, в котором всё конечно
Вообще-то как раз окружающий нас мир бесконечен в обе стороны (макромир и микромир). И во времени тоже.
UFO just landed and posted this here
Например, мы доказали, что существуют множества больше континуума. Какой в этом смысл? Всё, что мы узнали, так это то, что с помощью выбранных аксиом и правил вывода можно доказать данное утверждение. То есть, помимо собственной доказуемости данное утверждение не несёт в себе никакого смысла. Теория множеств – эта теория о самой себе, она не имеет пользы ни для других областей математики, ни для чего бы то ни было ещё.
Смысл в том, что между множеством с мощностью больше континуума и континуальным множеством нельзя построить взаимооднозначное соответствие. Математика — она не о числах, а о соотношениях.
UFO just landed and posted this here
В отличие от окружающего нас мира, в котором всё конечно, в математике мы часто сталкиваемся с бесконечными объектами.
Фраза требует не большего пояснения. Математики рассматривают бесконечность не просто так. Дело в том, что «как правило» введение бесконечности значительно упрощает исследуемый объект. Хотя это звучит странно, но надо понимать, что «бесконечность» это «математическая абстракция», которую тяжело представить, но за то с ней легче работать.
Кстати говоря, в обычной аксиоматике ZF вопреки часто встречающимуся заблуждению объединение счётного кол-ва счётных множеств счётным быть не обязано. Это соотношение зависит от ксиомы выбора.
Зависит от определения «счетного множества». Если определять как множество, для которого существует биекция на множество натуральных чисел — то да, есть проблемы (хотя достаточно счетной аксиомы выбора, которая слабее полной). Если же определять счетное множество как множество вместе с биекцией на натуральные, то никакой проблемы нет. В приложениях же почти всегда можно заранее зафиксировать эти биекции для всех рассматриваемых множеств из набора.
Какие-то символы не отображаются (Chrome):
Это проблема не Хрома, а шрифта, используемого вашей системой для отображения — видимо, в нём отсутствуют эти символы. У меня Хром (и Хромиум) под Линуксом — всё видно.
Я не математик и не знаю, как правильно называются отсутствующие у вас символы в математике, могу только описать их: выглядят они как 1) латинская буква
Я не математик и не знаю, как правильно называются отсутствующие у вас символы в математике, могу только описать их: выглядят они как 1) латинская буква
I, у которой вертикальная черта двойная, 2) латинская буква A, у которой правая косая черта двойная.Мне в школе еще была интересна формула пересчета рациональных чисел. И я реализовал ее: RationalNumberCounting. Для целых чисел все несколько попроще:
z: -3 -2 -1 0 +1 +2 +3;
n: 7 5 3 1 2 4 6;
z = (-1)^n * (n div 2)
z: -3 -2 -1 0 +1 +2 +3;
n: 7 5 3 1 2 4 6;
z = (-1)^n * (n div 2)
Сложновато изложено для школьников, сухо и без драйва. Школьники всё-таки, хоть и математики.
Формул и спец. обозначений многовато для темы, где нужно максимум примеров и минимум формул.
Формул и спец. обозначений многовато для темы, где нужно максимум примеров и минимум формул.
Sign up to leave a comment.
Конечное и бесконечное в математике. Лекция Павла Кожевникова для старшеклассников в Яндексе