Comments 47
Было бы круто, если бы цифры можно было перетаскивать из заданного набора (причем разных). А то так чет с кнопками не алё.
Когда считаю «10 — 10», он пишет "-0", немного странно.
Ох, а «99 — 99» он не может посчитать, неправильные ответы выдаёт. То 10, то 32.
Ох, а «99 — 99» он не может посчитать, неправильные ответы выдаёт. То 10, то 32.
68-62=0, ок
Прикольно, но непонятен практический смысл этой работы. Я бы вам предложил попробовать собрать нейросеть для символьных вычислений, типа такой arxiv.org/abs/1912.01412. Может быть можно будет её развить до уровня, когда она сможет сама доказывать теоремы? :)
56 — 57
Будущее здесь. Примерно так через 30 лет будет вычисляться операция a+b на устройствах. А мы, старики, будем неодумевать, почему никого не беспокоит такая грандиозная неэффективность.
И если вам кажется это бредом – предлагаю посчитать сколько времени тратится на вычисление a+b в Python и сравнить это с одной ассемблерной инструкцией.
Так что спасибо Яндекс что приоткрыл всем нам дорогу в ад.
И если вам кажется это бредом – предлагаю посчитать сколько времени тратится на вычисление a+b в Python и сравнить это с одной ассемблерной инструкцией.
Так что спасибо Яндекс что приоткрыл всем нам дорогу в ад.
Как я понимаю — натренировали сеть на распознавание всех комбинаций двузначных чисел (10000 комбинаций), каждой комбинации сопоставили ответ, далее выдают это за достижение.
А чем это достижение отличается от распознавания китайских иероглифов? Иероглифов больше, чем 10000.
Надо бы включать самокритику до публикации, а то вот приходится подключаться…
А чем это достижение отличается от распознавания китайских иероглифов? Иероглифов больше, чем 10000.
Надо бы включать самокритику до публикации, а то вот приходится подключаться…
95+95=180
Вопрос, нафига? Любому человеку, кто работает с нейросетями и так понятно что это возможно сделать, даже ради чистой науки.
30 — 30 выдает 10 с разной степенью стёртости единицы. Иногда ее почти не видно, и на выходе как бы 0, но в основном получается 10.
Сначала подумал, что первоапрельская шутка.
Эх, всё прекрасно, но вот наличие у статьи лишь одного автора сильно бросается в глаза. Ещё и глаз спотыкается об эти «we».
Видимо невнимательно прочитал статью, не нашел информацию о точности
Первая же попытка на tfjs: 11-2=19. На /calc 11-2=0.
Мда.
Мда.
Заготовка для разгадывателя капч? :)
Вроде попадались где-то такие арифметические
Вроде попадались где-то такие арифметические
С аугментацией данных явно проблем не было:-)
Теперь на этом калькуляторе можно сэмулировать не очень большую нейронную сеть.
Некоторые цифры напоминают ответы некоторых школьников у доски: если не можешь сосчитать нужно пробормотать под нос что-то невнятное типа «бырбырнадцать» :)
22-22=?
22-22=?
Заголовок спойлера

вызывает сомнение, что данный калькулятор действительно освоил арифметику с 2значными числами. более похоже, что он освоил какую картинку надо рисовать в ответ на другую картинку. освоить арифметику, это если бы он учился на двузначных числах, а в результате мог оперировать значительно более многозначными, со всякими высокоуровневыми правилами, типа сдвига разрядов и т д. а так — в нейросети в неявном виде хранятся просто все варианты. ее ведь так и учили, на куче сгенерированных картинок с правильными ответами.
Хорошее замечание =)
Действительно, в этом случае она могла просто попытаться всё запомнить. Чтобы проверить знания арифметики, нужны примеры посложнее. Я пробовал учить сетку решать выражения вплоть до 9-значного входа (например «56789+456») – сетка обучается, но начинает чаще ошибаться в простых примерах, типа «2+2». Возможно, более правильные лоссы/перевзвешивание выборки могли бы помочь.
В работе arxiv.org/abs/1506.02264 коллегам удалось в более простой постановке задачи поддержать сложение и вычитание 7-значных чисел (с долей ошибок 2-3%). В то же время, авторам не удалось поддержать умножение (72% ошибок). Если бы сети хватало capacity просто запомнить все ответы, то разницы бы не было. Похоже, что сеть все-таки действительно может освоить сложение и вычитание просто из парных ответов. Если у кого-то получится поддержать умножение, то это потянет на настоящую научную работу)
Действительно, в этом случае она могла просто попытаться всё запомнить. Чтобы проверить знания арифметики, нужны примеры посложнее. Я пробовал учить сетку решать выражения вплоть до 9-значного входа (например «56789+456») – сетка обучается, но начинает чаще ошибаться в простых примерах, типа «2+2». Возможно, более правильные лоссы/перевзвешивание выборки могли бы помочь.
В работе arxiv.org/abs/1506.02264 коллегам удалось в более простой постановке задачи поддержать сложение и вычитание 7-значных чисел (с долей ошибок 2-3%). В то же время, авторам не удалось поддержать умножение (72% ошибок). Если бы сети хватало capacity просто запомнить все ответы, то разницы бы не было. Похоже, что сеть все-таки действительно может освоить сложение и вычитание просто из парных ответов. Если у кого-то получится поддержать умножение, то это потянет на настоящую научную работу)
Вот все комбинации семизначных чисел мне кажется она просто запомнить не сможет, и придется именно разбираться в правилах. хотя не ясно, почему появилась проблема с умножениями, ведь в результате умножений получается числа имеющие больше разрядов, чем исходные, как и в случае сложения. а в случае вычитания разрядов может стать меньше. не понимаю, почему сетке не без разницы. Почему правило сложения с ее точки зрения проще, чем правило умножения…
С другой стороны, мне кажется порочным путь, в которым мы учим сетку отдельно складывать однозначные, двузначные, трезначные, однозначные с двузначными, однозначные с трехначными. Подсовывая такие выборки может статься, что она вычленит именно правила например сложения двузначных с однозначными, а остальные (например, однозначные с однозначными) позабудет. Именно это, скорее всего вы и наблюдали, когда сетка стала ошибаться в простых примерах. То есть вы как бы переобучали ее на больших примерах вытесняя правила маленьких примеров. А общая логика, которая работала бы для любых примеров ею схвачена не была изначально. Может быть это можно решить увеличением количества слоев, или чем то в этом роде.
С другой стороны, мне кажется порочным путь, в которым мы учим сетку отдельно складывать однозначные, двузначные, трезначные, однозначные с двузначными, однозначные с трехначными. Подсовывая такие выборки может статься, что она вычленит именно правила например сложения двузначных с однозначными, а остальные (например, однозначные с однозначными) позабудет. Именно это, скорее всего вы и наблюдали, когда сетка стала ошибаться в простых примерах. То есть вы как бы переобучали ее на больших примерах вытесняя правила маленьких примеров. А общая логика, которая работала бы для любых примеров ею схвачена не была изначально. Может быть это можно решить увеличением количества слоев, или чем то в этом роде.
del
Что-то подобное есть в приложении Photomath для решения математических примеров, там распознавание рукописного ввода очень даже ничего.
Сеть, бывают случаи, что просто наглухо не видит некоторые цифры.
А перед нулём может, с чего-то, становиться + или -, а то и они оба…
Картинка №1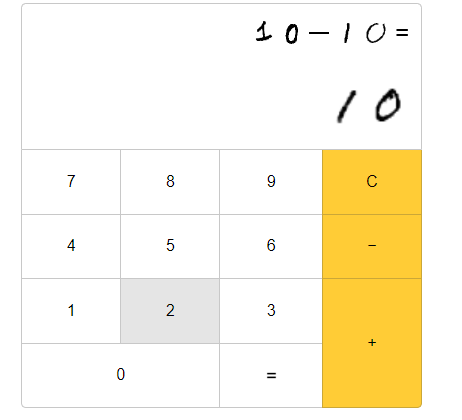

А перед нулём может, с чего-то, становиться + или -, а то и они оба…
77-11=-66
Мы взяли за основу UNet-подобную архитектуру,… убрали все skip-connections и добавили несколько полносвязных слоёв в ботлнек-модели. Это сделало модель больше не похожей на UNet.— да это же… автоэнкодер! )
Sign up to leave a comment.




Нейросетевой калькулятор для сложения и вычитания не очень больших чисел