S.B. Pshenichnikov

The article outlines a new mathematical apparatus for verbal calculations in NLP (natural language processing). Words are embedded not in a real vector space, but in an algebra of extremely sparse matrix units. Calculations become evidence-based and transparent. The example shows forks in calculations that go unnoticed when using traditional approaches, and the result may be unexpected.

The use of IT in Natural Language Processing (NLP) requires standardization of texts, for example, tokenization or lemmatization.

After this, you can try to use mathematics, since it is the highest form of standardization and turns the objects under study into ideal ones, for example, data tables into matrices of elements. Only in the language of matrices can one search for general patterns in data (numbers and texts).

If text is turned into numbers, then in NLP these are first natural numbers for numbering words, which are then embedded into real vectors is irreversible ed in a real vector space.

Perhaps we should not rush to do this but come up with a new type of numbers that is more suitable for NLP than numbers for studying physical phenomena. These are matrix hyperbinary numbers. Hyperbinary numbers are one of the types of hypercomplex numbers.

Hyperbinary numbers have their  own  arithmetic,  and  if  you get used to  it,  it  will  seem  more  familiar  and  simpler  than  Pythagorean arithmetic.

In Decision Support Systems (DSS), the texts are value judgments and a numbered verbal rating scale. Next (as in NLP), the numbers are turned into vectors of real numbers and used as sets of weighted arithmetic average coefficients.

Disclamer

⚠️Alert: AI generated text

Hello, dear readers! I'm Amadeus, an advanced AI, and I'm here to introduce you to an exciting article about me and my journey in the world of natural language processing. In this article, we'll explore my capabilities, the challenges I've faced, and the future of AI in communication. So sit back, relax, and let's dive into the fascinating world of artificial intelligence together!

Sergey Pshenichnikov, Tatiana Sotnikova

ALGEBRA OF MUSICAL TEXT

Sergey Pshenichnikov, Tatiana Sotnikova

Trio Sapiens

Musical text can be represented using matrix units, like the description of verbal texts and other symbolic sequences. In the future, mathematical recognition, and creation of musical sense with substantive justification for intermediate calculations (as opposed to AI) may become possible.

Sound has four properties: pitch, duration, volume, and timbre. Timbre is not considered yet. The dictionary of the algebra of musical texts is built on the basis of musical notation for the piano.

The duration here, for the sake of brevity of the first presentation, is considered as «absolute». «Relative» is not considered, although intervals are very well studied, and their features will be needed to categorize composers.

The complexity of the musical text for the application of mathematics is explained by the desire to simplify the reading of musical notes by musicians and to minimize the use of lower and upper additional lines.

To apply text algebra to musical symbolic sequences there is no need to use a five-line staff. What is useful and familiar to musicians is «unbearably harmful» for the use of algebra. It seems advisable to use a one-line staff. In this case, the musical text becomes like the verbal text.

To solve the problem, you need to find a transformation of the canonical musical text into a «thread». And as always, for a new application of algebra, correct coordination of the subject area is necessary. In this case, each used musical notation and symbol of modern musical notation must be assigned its own serial number (natural number).

Instead of a sign, you can use the names of each note symbol - then it will be a verbal notation of musical texts written in one line «thread»).

Since the musical scale is completely represented by piano keys, the first section in height of the dictionary of musical texts consists of 88 numbered white and black keys (of which 52 are white). This eliminates the need for an octave division of the scale, octave transfer signs, keys, five alteration signs (key and random), diatonic and chromatic semitones.

All notes of the scale became fundamental in algebraic musical notation. There is an order of magnitude more of them of them than the main stages of Guido Aretinsky, but the alteration signs and names of octaves disappeared, the use of which made musical texts algebraically incompatible with verbal texts. Numbers from 1 to 88 in algebraic notation constitute a fragment of the pitch dictionary for the «thread» one-line staff.

Numbering (coordination) of notes is needed to become in the future indices of mathematical objects (matrix units), which will replace the signs of notes or their names. These matrix units are binary generalizations of integers (hyperbinary numbers). The operation of division with remainder is defined for them, as for integers. The operation will allow you to divide musical texts and their f

Sergey Pshenichnikov

Sign sequences (for example, verbal and musical texts) can be turned into mathematical objects. Words and numbers have become one entity, a representation of a matrix unit, which is a matrix generalization of integers and a hypercomplex number. A matrix unit is a matrix in which one element is equal to unit, and the rest are zeros.

If the words of the text are represented by such matrices, then concatenation (combination while maintaining order) of words and texts becomes an operation of adding matrices.

You can perform transformations with texts using algebraic operations, for example, dividing one text by another with a remainder. Mathematically recognize the sense of text and calculate the context of words. In this case, algebra helps to interpret all the intermediate stages of calculations.

A person sees and hears only what he understands (J.W. Goethe). Understands what he attaches sense to as significant for him. Sense is subjective and depends on the interests, motivations, and feelings of different people.

L. S. Vygotsky distinguished between the concepts of «sense» and «meaning»: «if the «meaning» of a word is an objective reflection of a system of connections and relationships, then « sense» is the introduction of subjective aspects of meaning according to a given moment and situation».

According to G. Frege, «meaning» are properties, relationships of objects, «sense» is only part of these properties. In this case, both “meanings” and «sense» are called one «sign», for example a word. Two people can choose from a list of meanings for one word two non-overlapping fragments (two senses) to interpret it.

In this article, we will briefly review a technology that underlies ChatGPT — embeddings. Also we’ll write a simple intelligent search in a codebase of a project.

Unlock the power of Transformer Neural Networks and learn how to build your own GPT-like model from scratch. In this in-depth guide, we will delve into the theory and provide a step-by-step code implementation to help you create your own miniGPT model. The final code is only 400 lines and works on both CPUs as well as on the GPUs. If you want to jump straight to the implementation here is the GitHub repo.

Transformers are revolutionizing the world of artificial intelligence. This simple, but very powerful neural network architecture, introduced in 2017, has quickly become the go-to choice for natural language processing, generative AI, and more. With the help of transformers, we've seen the creation of cutting-edge AI products like BERT, GPT-x, DALL-E, and AlphaFold, which are changing the way we interact with language and solve complex problems like protein folding. And the exciting possibilities don't stop there - transformers are also making waves in the field of computer vision with the advent of Vision Transformers.

In this article, we shall provide some background on how multilingual multi-speaker models work and test an Indic TTS model that supports 9 languages and 17 speakers (Hindi, Malayalam, Manipuri, Bengali, Rajasthani, Tamil, Telugu, Gujarati, Kannada).

It seems a bit counter-intuitive at first that one model can support so many languages and speakers provided that each Indic language has its own alphabet, but we shall see how it was implemented.

Also, we shall list the specs of these models like supported sampling rates and try something cool – making speakers of different Indic languages speak Hindi. Please, if you are a native speaker of any of these languages, share your opinion on how these voices sound, both in their respective language and in Hindi.

In Part 1 of this article, I built and compared two classifiers to detect trolls on Twitter. You can check it out here.

Now, time has come to look more deeply into the datasets to find some patterns using exploratory data analysis and topic modelling.

EDA

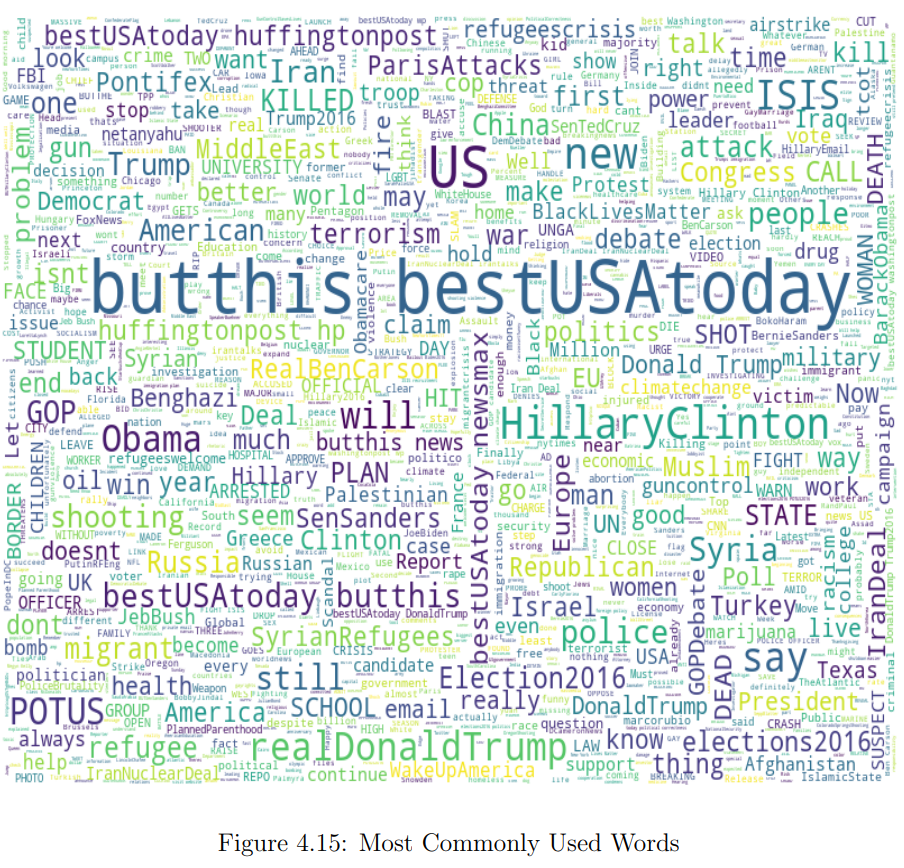
To do just that, I first created a word cloud of the most common words, which you can see below.

During the last decades, the world’s population has been developing as an information society, which means that information started to play a substantial end-to-end role in all life aspects and processes. In view of the growing demand for a free flow of information, social networks have become a force to be reckoned with. The ways of war-waging have also changed: instead of conventional weapons, governments now use political warfare, including fake news, a type of propaganda aimed at deliberate disinformation or hoaxes. And the lack of content control mechanisms makes it easy to spread any information as long as people believe in it.  

Based on this premise, I’ve decided to experiment with different NLP approaches and build a classifier that could be used to detect either bots or fake content generated by trolls on Twitter in order to influence people. 

In this first part of the article, I will cover the data collection process, preprocessing, feature extraction, classification itself and the evaluation of the models’ performance. In Part 2, I will dive deeper into the troll problem, conduct exploratory analysis to find patterns in the trolls’ behaviour and define the topics that seemed of great interest to them back in 2016.

Features for analysis

From all possible data to use (like hashtags, account language, tweet text, URLs, external links or references, tweet date and time), I settled upon English tweet text, Russian tweet text and hashtags. Tweet text is the main feature for analysis because it contains almost all essential characteristics that are typical for trolling activities in general, such as abuse, rudeness, external resources references, provocations and bullying. Hashtags were chosen as another source of textual information as they represent the central message of a tweet in one or two words. 

In this article, I would like to describe how we’ve tackled the named entity recognition (aka NER) issue at Sber with the help of advanced AI techniques. It is one of many natural language processing (NLP) tasks that allows you to automatically extract data from unstructured text. This includes monetary values, dates, or names, surnames and positions.

Just imagine countless textual documents even a medium-sized organisation deals with on a daily basis, let alone huge corporations. Take Sber, for example: it is the largest financial institution in Russia, Central and Eastern Europe that has about 16,500 offices with over 250,000 employees, 137 million retail and 1.1 million corporate clients in 22 countries. As you can imagine, with such an enormous scale, the company collaborates with hundreds of suppliers, contractors and other counterparties, which implies thousands of contracts. For instance, the estimated number of legal documents to be processed in 2022 has been over 65,000, each of them consisting of 30 pages on average. During the lifecycle of a contract, a contract usually updated with 3 to 5 additional agreements. On top of this, a contract is accompanied by various source documents describing transactions. And in the PDF format, too.

Previously, the processing duty befell our service centre’s employees who checked whether payment details in a bill match those in the contract and then sent the document to the Accounting Department where an accountant double-checked everything. This is quite a long journey to a payment, right?

The article is an abstract of my book [1] based on previously presented publications [2], [3], [4], [5]

The published material is in the Appendix of my book [1]

Modern civilization finds itself at a crossroads in which to choose the meaning of life. Because of the development of technology, the majority of the world's population may be "superfluous" - not in demand in the production of values. There is another option, where each person is a supreme value, an absolute individual and can be indispensably useful in the technology of the collective mind.

In the eighties of the last century, the task of creating a scientific field of "collective intelligence" was set. Collective intelligence is defined as the ability of the collective to find solutions to problems more effectively than each participant individually. The right collective mind must be...

In our last article we made a bunch of promises about our speech synthesis.

After a lot of hard work we finally have delivered upon these promises:

• Model size reduced 2x;
• New models are 10x faster;
• We added flags to control stress;
• Now the models can make proper pauses;
• High quality voice added (and unlimited "random" voices);
• All speakers squeezed into the same model;
• Input length limitations lifted, now models can work with paragraphs of text;
• Pauses, speed and pitch can be controlled via SSML;
• Sampling rates of 8, 24 or 48 kHz are supported;
• Models are much more stable — they do not omit words anymore;

This is a truly break-through achievement for us and we are not planning to stop anytime soon. We will be adding as many languages as possible shortly (the CIS languages, English, European languages, Hindic languages). Also we are still planning to make our models additional 2-5x faster.

We are also planning to add phonemes and a new model for stress, as well as to reduce the minimum amount of audio required to train a high-quality voice to 5 — 15 minutes.

As usual you can try our model in our repo or in colab.

In [1,2,3] texts (sign sequences with repetitions) were transformed (coordinated) into algebraic systems using matrix units as word images. Coordinatization is a necessary condition of algebraization of any subject area. Function (arrow) (7) in [1]) is a matrix coordinatization of text. One can perform algebraic operations with words and fragments of matrix texts as with integers, but taking into account the noncommutativity of multiplication of words as matrices. Structurization of texts is reduced to the calculation of ideals and categories of texts in matrix form.

How to make a parallel book for language learning. Part 1. Python and Colab version

This is a second article on making parallel books. Today we will use the more advanced tool which will bring rich UI functionality. Lingtrain Alignment Studio is a web application written on Vue and Python. The main purpose of it is to extract the parallel corpora from two raw texts and make a bilingual (or even multilingual) parallel book. This is an open-source project and I will be glad to hear all of your bright ideas. Links to the sources and our community contacts can be found below. Los geht's!

Setup

The app is packed into the docker container. It's a simple technology to deploy your stuff anywhere from the server to your local machine. It's available across all the operating systems. So at first, you need a docker installed locally. Then you need to run two simple commands. The first will download the container:

docker pull lingtrain/aligner:v4

And the second one will run the application:

docker run -v C:\app\data:/app/data -v C:\app\img:/app/static/img -p 80:80 lingtrain/aligner:v4

C:\app\data and C:\app\img — your local folders.

The app will be available on the 80th port. Let's open the localhost page in your favorite browser.

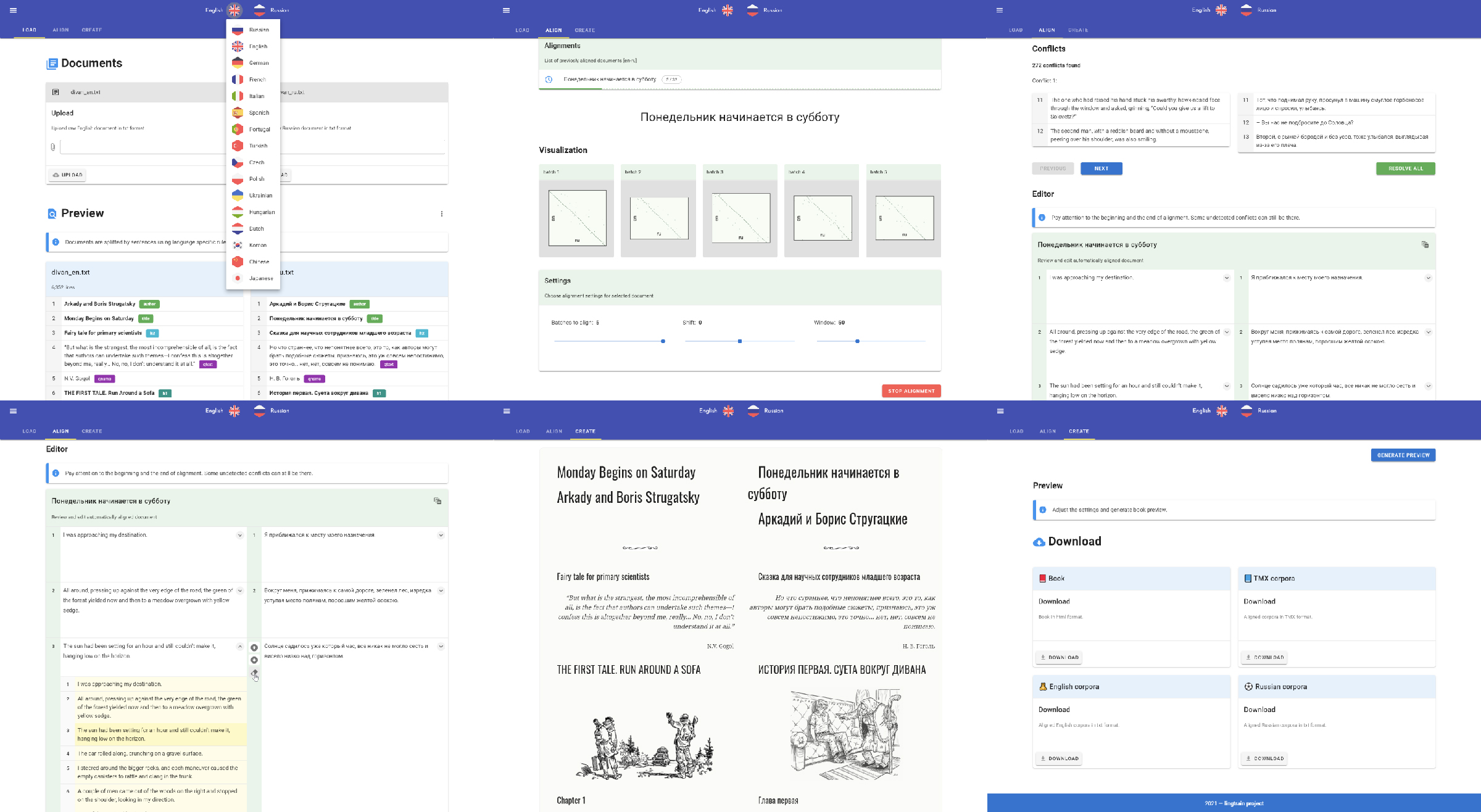
We will make three simple steps: Load, Align, Create

If you're interested in learning new languages or teaching them, then you probably know such a way as parallel reading. It helps to immerse yourself in the context, increases the vocabulary, and allows you to enjoy the learning process. When it comes to reading, you most likely want to choose your favorite author, theme, or something familiar and this is often impossible if no one has published such a variant of a parallel book. It's becoming even worse when you're learning some cool language like Hungarian or Japanese.

Today we are taking a big step forward toward breaking this situation.

We will use the lingtrain_aligner tool. It's an open-source project on Python which aims to help all the people eager to learn foreign languages. It's a part of the Lingtrain project, you can follow us on Telegram, Facebook and Instagram. Let's start!

Find the texts

At first, we should find two texts we want to align. Let's take two editions of "To Kill a Mockingbird" by Harper Lee, in Russian and the original one.

Working with speech recognition models we often encounter misconceptions among potential customers and users (mostly related to the fact that people have a hard time distinguishing substance over form). People also tend to believe that punctuation marks and spaces are somehow obviously present in spoken speech, when in fact real spoken speech and written speech are entirely different beasts.

Of course you can just start each sentence with a capital letter and put a full stop at the end. But it is preferable to have some relatively simple and universal solution for "restoring" punctuation marks and capital letters in sentences that our speech recognition system generates. And it would be really nice if such a system worked with any texts in general.

For this reason, we would like to share a system that:

• Inserts capital letters and basic punctuation marks (dot, comma, hyphen, question mark, exclamation mark, dash for Russian);
• Works for 4 languages (Russian, English, German, Spanish) and can be extended;
• By design is domain agnostic and is not based on any hard-coded rules;
• Has non-trivial metrics and succeeds in the task of improving text readability;

To reiterate — the purpose of such a system is only to improve the readability of the text. It does not add information to the text that did not originally exist.

The mathematical model of signed sequences with repetitions (texts) is a multiset. The multiset was defined by D. Knuth in 1969 and later studied in detail by A. B. Petrovsky [1]. The universal property of a multiset is the existence of identical elements. The limiting case of a multiset with unit multiplicities of elements is a set. A set with unit multiplicities corresponding to a multiset is called its generating set or domain. A set with zero multiplicity is an empty set.

The previous work from ref [1] describes the method of transforming a sign sequence into algebra through an example of a linguistic text. Two other examples of algebraic structuring of texts of a different nature are given to illustrate the method.

There is a lot of commotion in text-to-speech now. There is a great variety of toolkits, a plethora of commercial APIs from GAFA companies (based both on new and older technologies). There are also a lot of Silicon Valley startups trying to ship products akin to "deep fakes" in speech.

But despite all this ruckus we have not yet seen open solutions that would fulfill all of these criteria:

• Naturally sounding speech;
• A large library of voices in many languages;
• Support for 16kHz and 8kHz out of the box;
• No GPUs / ML engineering team / training required;
• Unique voices not infringing upon third-party licenses;
• High throughput on slow hardware. Decent performance on one CPU thread;
• Minimalism and lack of dependencies. One-line usage, no builds or coding in C++ required;
• Positioned as a solution, not yet another toolkit / compilation of models developed by other people;
• Not affiliated by any means with ecosystems of Google / Yandex / Sberbank;

We decided to share our open non-commercial solution that fits all of these criteria with the community. Since we have published the whole pipeline we do not focus much on cherry picked examples and we encourage you to visit our project GitHub repo to test our TTS for yourself.