
Данная статья предназначена для ознакомления с базовой математической составляющей компьютерной многомерной графики. На примере симплекса Серпинского в статье рассматриваются вопросы построения, перемещения, проецирования и отображения сложных многомерных геометрических фигур.
Также имеются картинки, видео, исходники, и уверяю вас, что всё очень просто, читайте, вникайте.
Что такое треугольник Серпинского, и что такое пирамида Серпинского весьма понятно. Но что такое симплекс Серпинского? Для начала, для тех кто не прочитал в вики, что такое симплекс — скажу просто, что симплекс это n-мерный тетраэдр (см. видео). Ну а симлекс Серпинского — некий фрактал, построенный по аналогии с треугольником и тетраэдром Серпинского.
Построение равностороннего симплекса
Не поверите, но это самое сложное среди всего, что есть в этой статье (по моим оценкам). А ведь всё, что нам нужно — это n точек в n-1 мерном пространстве, равноудаленных друг от друга и от центра. Прежде, чем читать дальше, строго рекомендую подумать, как бы вы строили такие точки?
Конечно же нас интересуют случаи, где n >= 3, иначе просто не интересно. Каждую n-тую точку будем строить на основе всех предыдущих. Для начала, нам понадобится построить обычный равносторонний треугольник:

Для того, чтобы добавить новую точку — нужно новое измерение (обозначим W). Введя это измерение, для того, чтобы точка была равноудалена от всех других точек, установим для этой точки Pn значение q1 по оси W, а остальным точкам по оси W — -q2. Остальные координаты осей для точки Pn оставим нулевыми. Что получается? Что все точки, что были — остаются на равном расстоянии друг от друга и от центра, а новая точка равноудалена от всех остальных. Осталось лишь подобрать такие q1, q2, чтобы все точки были равноудалены друг от друга, и от центра.

l — расстояние между точками — неизменно, и вычисляется после построения треугольника.
d — расстояние от точек до центра — меняется, и вычисляется перед добавлением новой точки.
Первое уравнение указывает на то, что расстояния от принятых точек до новой должны быть одинаковыми.
Второе — что расстояния до центра должны быть одинаковыми.
Собственно, таким образом и получаем равносторонний симплекс.
Исходники:
double c = r * sqrt(3) / 2;
double l = c * 2; //distance between points
points[0][0] = + 0; points[0][1] = + r; //first point
points[1][0] = + c; points[1][1] = - r / 2; //second point
points[2][0] = - c; points[2][1] = - r / 2; //3th point
for (int i = 3; i <= dimensionalCount; i++)
{
double d = points[0].distanceToCenter();
double q2 = (l * l - 2 * d * d) / (2 * sqrt(l * l - d * d));
double q1 = sqrt(d * d + q2 * q2);
for (int k = 0; k < i; k++)
{
points[k][i-1] = -q2; //set i-th dimension for all created points
points[i][k] = 0; //set all calculated dimension for new point
}
points[i][i-1] = q1;
}
Фракталим
Очень легко можно заметить, что и треугольник (n=2) и тетраэдр (n=3) Серпинского создаются из базовой фигуры методом замены базовой фигуры на n+1 таких же, но поменьше. В каждой из новых фигур за основу берется одна точка базовой фигуры, остальные точки — центры масс отрезков, что включают данную точку. В принципе, всё очень просто и понятно.
Так и запишем:
void rec(QVector<Simplex>& storage, const Simplex& current, int recursionDepth)
{
if (recursionDepth == maxRecursionDepth)
storage.append(current);
else
{
for (int i = 0; i <= n; i++)
{
Simplex newTriangle(current.dimensionsCount());
for (int k = 0; k <= n; k++)
{
if (i == k)
newTriangle[k] = current[i];
else
newTriangle[k] = (current[i] + current[k]) / 2.0;
}
rec(storage, newTriangle, recursionDepth + 1);
}
}
}
Как видите, тут нигде нет опоры на размерность пространства, и оно корректно отрабатывает и для 2D и для 3D:


Поворот & проекция
Вращать можно сложно (кватернионы, матричные преобразования), а можно просто… Мы будем делать всё просто, последовательно вращать по каждым двум координатам. Для 2D это можно воспринимать как поворот вокруг точки, для 3D — вокруг прямой, для ND — вокруг (N-2)-размерного пространства. Собственно, формула поворота высчитывается очень просто:
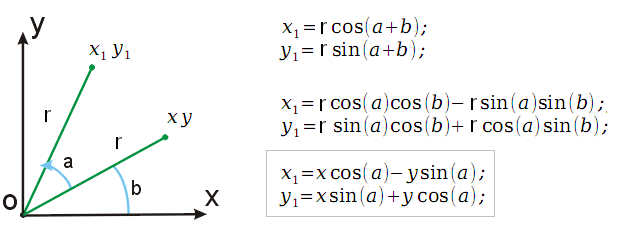
Ну и программируется это еще проще:
for (int i = 0; i < coordinates.count(); i++)
for (int k = i + 1; k < coordinates.count(); k++)
{
ratio = sqrt(2 + i * coordinates.count() + k);
p1 = temp[i] * cos(angle * ratio) - temp[k] * sin(angle * ratio);
p2 = temp[k] * cos(angle * ratio) + temp[i] * sin(angle * ratio);
temp[i] = p1;
temp[k] = p2;
}
Где ratio — коэффициент, для того, чтобы вращение в разные стороны было с разными скоростями, желательно без зацикливаний. temp[i] — і-ая координата текущей точки.
Проекция — самый сложный момент работы с многомерными пространствами. Причин много:
1. Никто не привык понимать многомерные геометрические объекты.
2. Оптика физики молчит по этому поводу (насколько я знаю).
3. Куча разных методов и все перегружают картинку, и непонятно, что корректней.
Мы возьмем самый простой метод — перспективная проекция. Будем проецировать n-мерную точку на (n-1) пространство… Таким образом, каждый раз понижая N — дойдем до того, что точка уже двухмерная или трехмерная и уже можно отображать.
На примере 2D to 1D попробуем просчитать формулу перспективной проекции.
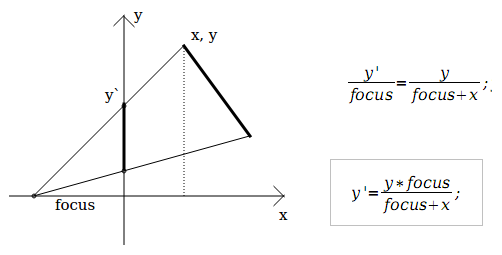
Видно, что с помощью 2 координат и некой константы focus можно сделать 1 координату. И формула очень простая, как и код:
for (int i = coordinates.count() - 1; i > 3; i--)
for (int k = 0; k < i; k++)
temp[k] *= focus / (focus + temp[i]);
Насколько это всё корректно? Вообще не корректно, ни разу, ни капли! Но судя по тому, что есть в инете, что-то очень похожее используется другими программистами. Вот, например, тессеракт, полученый таким методом проецирования:
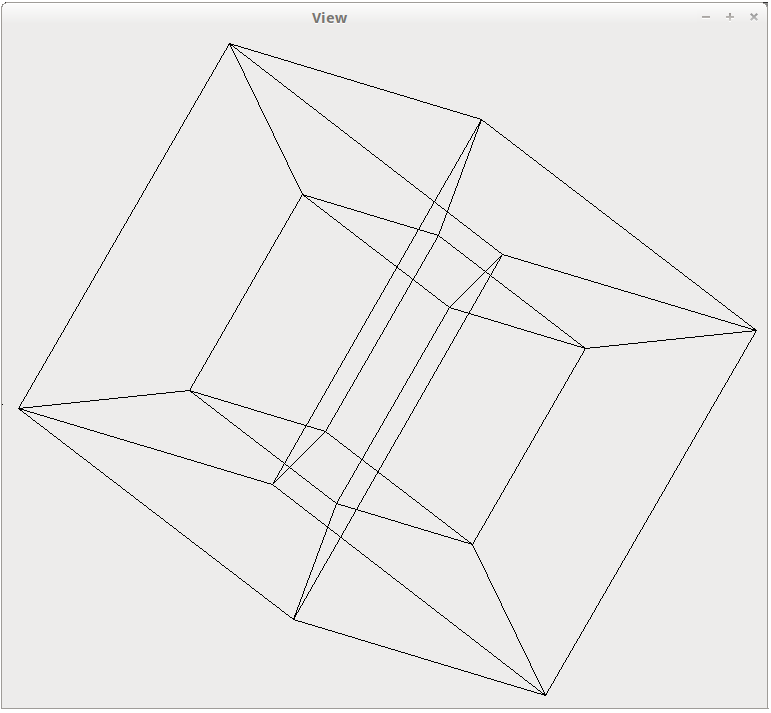
Рендеринг
QPainter — самый простой способ, что заключается в использовании стандартных средств среды разработки, для прорисовки всего обычными линиями, без освещения, заливки треугольников, прочего. В моих исходниках он включен по умолчанию, и будет работать везде, где есть Qt (Windows, Linux, Mac OS...).
Собственно, вот так выглядит код рендеринга:
QPoint center(this->width() / 2, this->height() / 2);
foreach(const Simplex& simplex, simplexes)
for (int i = 0; i < simplex.dimensionsCount() + 1; i++)
for (int k = i+1; k < simplex.dimensionsCount() + 1; k++)
p.drawLine(simplex[i].to2D(focus, angle) + center, simplex[k].to2D(focus, angle) + center);
Как видите, нет ничего проще… Но нам нужно, чтобы было красиво, так ведь?
OpenGL, DirectX — прогрессивный метод, что позволяет в real time рендерить всё красиво. Но есть беда: без прозрачности красивым ничего не будет, а прозрачность у этих двух монстров предполагает, что рендерить нужно от далекого (z -> max) к близкому (z -> min). Для этого, каждый кадр, треугольники нужно сортировать, а их в моем примере порядка 6000. Ну это не беда, беда в том, что в общем случае нельзя определить, какой треугольник ближе, а какой дальше. Более того, когда мы говорим о проекции с многомерного пространства, мы говорим о том что треугольники пересекаются. В итоге их нужно резать и сортировать каждую итерацию, что уже весьма сложно…
Этот метод я не реализовывал.
Трассировка лучей — то, что доктор прописал. Эта технология позволит получить картинку максимального качества и имеет недостаток только в скорости. Но, по сути, real time нам и не нужен.
Для трассировки я использовал POV-Ray, который идеально подошел для этой задачи лишь тем, что умеет запускаться с командной строки, без всякого там GUI.
Для использования сего чуда, я написал некий шаблон, который программой заполняется нужными точками, и на выходе получается готовый к трассировке .pov файл. Шаблон по набору точек строит треугольники и рамки, и очень прост по своей структуре:
#declare ppp = array[<<!!--count of points--!!>>]
{
<<!!--Main Array of points--!!>>
};
#declare i = 0;
#while(i < <<!!--count of points--!!>>)
#if (vlength(ppp[i] - ppp[i+1])!=0)
cylinder{ppp[i], ppp[i+1], 0.2
texture {pigment{color Gray}}
}
#end
#if (vlength(ppp[i] - ppp[i+2])!=0)
cylinder{ppp[i], ppp[i+2], 0.2
texture {pigment{color Gray}}
}
#end
#if (vlength(ppp[i+1] - ppp[i+2])!=0)
cylinder{ppp[i+1], ppp[i+2], 0.2
texture {pigment{color Gray}}
}
#end
polygon {4
ppp[i], ppp[i+1], ppp[i+2] ,ppp[i]
texture { Surface_Texture }}
#declare i=i+3;
#end
Собственно, на основе этого шаблона было сделано 1000 картинок с разными поворотами, из которых потом и было сделано вот это видео:
Исходники
Статья посвящается девушкам heavy metal коллектива Fight with Fate.