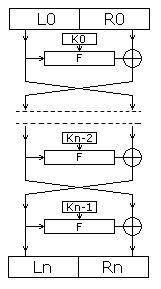
В продолжении статьи про blowfish хотелось бы поговорить про его основу — сеть Фейстеля. Люди «в теме» слышали про неё не одну сотню раз — эта сеть используется в подавляющем большинстве блочных шифров. Но вот вам, только честно, что нибудь понятно из картинки справа? Ну, допустим в одну сторону(шифрование) понятно, а обратно?
Если нет, то прошу под коврик
Для начала хотя бы бегло пробегитесь по викистатье, чтобы в общих чертах понять о чем речь
Для простоты будем работать с блоком, состоящим всего из двух байт. Как гласит википедия, его нужно попилить пополам и назвать левую часть L, а правую R. Да будет так.
И так, у нас есть две половинки блока, и таинственная функция F. Поехали
- Первое, что нам нужно усвоить — это то, что XOR (обозначается ⊕) — инволютивная операция. Не пинайтесь ногами, это всего лишь означает, что если поксорить одно число с другим дважды, то мы опять искомое получим. Т.е. A ⊕ B ⊕ B == A.
Отсюда следует, что можно выстраивать бесконечные цепочки A ⊕ B ⊕ C ⊕ D ⊕… и если мы перексорим всё в обратном порядке, то получим A.
Например, ((100 ⊕ 200) ⊕ 50) ⊕ 150= 8. Отсюда 8 ⊕ 150 ⊕ 50 ⊕ 200 = 100 - Второй важный момент — в один момент времени изменяется лишь одна половинка блока
- Теперь про «черный ящик» или функцию F. Функция F по идее может быть любой выдуманной функцией (хоть сложным хэшем, хоть тупо возвращающей 0), потому что когда мы будем в обратном порядке всё перексоривать(расшифровывать), то вторым аргументом у нас всегда будет тот же результат этой функции, что был в процессе шифрования. На практике же её создание сродни искусству и не дает 100% гарантии от новых методов криптоанализа.
Как этот «тот же» получается?
Рассмотрим на примере трех раундов по шагам
Шифрование
0) У нас есть L и R какие то числа Пусть они будут 100 и 200. и F, какая то функция, зависящая от L и номера раунда n. Пусть, к примеру, F будет просто складывать их по модулю 256(чтоб не вылезало за байт). Т.е. F(L, n) = (L+n) % 256. ( % это остаток от деления )
Раунд первый (n =1)
1) Берем R(200) и ксорим его с результатом функции F(L, n), т.е. 200 ⊕ ((100+1) % 256) получаем 173.
2) Ставим 173 на место L, а на место R предыдущее значение L (100), т.е. меняем местами R и результат ксора R с функцией F.
Раунд 2 (n = 2)
1) Теперь L = 173, R = 100. Ксорим 100 c ((173 + 2) % 256), получаем 203
2) Ставим 203 на место L, а 173 на место R.
Раунд 3 (n = 3)
1) L = 203, R = 173. Ксорим 173 c ((203 + 3) % 256), получаем 99
2) Поскольку раунд последний, то меняем только R (чтобы потом перестановку не делать)
После шифрования L = 203, R = 99.
Расшифровка
Идем в обратном порядке, номера раундов идут с 3 и до 1
Раунд 1 (n = 3)
1) L = 203, R = 99. Ксорим 99 с ((203 + 3) % 256) получаем 173. Знакомое число?
2) Ставим 173 на место L, 203 на место R
Раунд 2 (n = 2)
1) L = 173, R = 203. Отсюда 203 ⊕ ((173 + 2) % 256) = 100. Уже почти!
2) Меняем L = 100, R = 173
Раунд 3 (n = 1)
1) L = 100, R = 173. Считаем R(перестановка, как и в случае с шифрованием, не нужна) = 173 ⊕ ((100+1) % 256) = 200 УРАААА!!!
L = 100, R = 200. Как в аптеке )
То есть, вся сеть Фейстеля по сути сводится к поочередному ксору обеих половинок блока с какими то вычисляемыми значениями, которые во время шифрования подставляются в обратном порядке.
Ну и на последок код на java, реализующий описанный выше алгоритм.
public class BlockTest
{
private static int rounds = 3;
public void feist(int[] a, boolean reverse)
{
int round = reverse? rounds: 1;
int l = a[0];
int r = a[1];
for (int i = 0; i < rounds; i++)
{
if (i < rounds — 1) // если не последний раунд
{
int t = l;
l = r ^ f(l, round);
r = t;
}
else // последний раунд
{
r = r ^ f(l, round);
}
round += reverse? -1: 1;
}
a[0] = l;
a[1] = r;
}
private int f(int b, int k)
{
return b + k;
}
public void test()
{
int[] a = new int[2];
a[0] = 100;
a[1] = 200;
feist(a, false);
feist(a, true);
}
}
Надеюсь, вам понравилось ;)