
В статье описан простой алгоритм наведения пушки, когда оси вращения не пересекаются с осью ствола. Быстро найти готовый не получилось – пришлось вспоминать школьные времена. Ну а раз вспомнил – грех не поделиться с остальными. А кто-то где-то, сэкономив время, использует его на создание еще чего-то полезного…
Результат приведенных расчетов используется в аркадной игре. За месяц промахов не было. Если вы разрабатываете симулятор, скорее всего, понадобится что-то более изощренное.
Итак, дана пушка. При наведении турель может поворачиваться в горизонтальной (красная ось вращения на рисунке) и вертикальной (зеленая ось) плоскостях.
Свойства модели пушки
1. Ось ствола (обозначена синим цветом) не пересекается с осями вращения.
2. Ось ствола параллельна оси X
3. Направление выстрела совпадает с положительным направлением X
4. Ось горизонтального поворота (красная) параллельна оси Z, или оси совпадают
5. Ось вертикального поворота (зеленая) параллельна оси Y, или оси совпадают
6. Верх модели соответствует положительному направлению оси Z
Для успешного наведения на цель требуется вычислить два угла поворота – горизонтальный и вертикальный

Благодаря заданным ограничениям модели (оси поворотов параллельны или совпадают с соответствующими осями координат), задачу нахождения углов наведения в трехмерном пространстве можно разбить на две в двухмерном:
1. Угол горизонтального поворота может быть найден с использованием проекции модели на плоскость XY (Z=0)
2. Угол вертикального поворота – ось XZ (Y=0)
Решаться обе подзадачи будут одинаково.
Для начала рассмотрим исходное положение

A – центр вращения. Результат проекции оси поворота на перпендикулярную плоскость.
B – точка вылета снаряда.
Fire – проекция вектора направления выстрела.
C – позиция цели
Определим угол между вектором выстрела и AB

Здесь и далее угловыми скобками будет обозначаться скалярное произведение векторов.
Теперь предположим, что наведение завершено. При повороте на цель точка B перешла в D, а вектор Fire стал Fire1

Отсюда можно найти длину отрезка DC, используя теорему косинусов.

Где

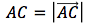
Перепишем формулу, чтобы она соответствовала общей форме квадратного уравнения

для неизвестного DC


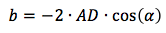
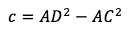
тогда

из двух получившихся значений DC нам подходит положительное.
Если DC получается отрицательным, то цель находится в недоступной (при использовании этого алгоритма по крайней мере) для наведения позиции.
Теперь рассмотрим рисунок, на котором изображены положения системы до и после наведения
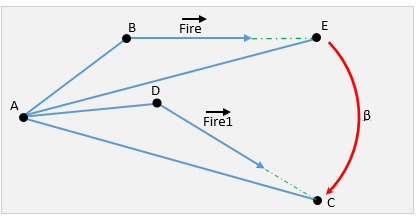
Красным обозначен искомый угол наведения.
Определим координату точки E. Это координата цели C, повернутая на угол прицеливания относительно центра A в противоположном направлении. Т.е это куда бы попала пушка, если бы выстрелила на правильное расстояние, забыв повернуться. Для этого нужно сдвинуть точку B в направлении вектора Fire на расстояние DC.
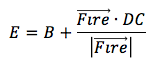
Тогда угол прицеливания – это угол между векторами AE и AC, который находится через скалярное произведение

Угол найден, но нужно помнить, что точка прицеливания может находиться где угодно, в том числе и «выше» направления выстрела. Т.е. нужно найти еще направление поворота.
Определим ориентацию векторов AE и AC. Двух векторов для этого недостаточно. Нужен третий вектор, перпендикулярный первым двум. Назовем его V. Именно его направление определяет позицию наблюдателя, который увидит поворот по или против часовой стрелки в зависимости от того, по какую сторону от плоскости с векторами AE и AC находится. Поскольку мы работаем с проекциями на координатные плоскости, искомый вектор будет параллелен третьей оси координат.
Для определенности рассмотрим пример проекции на ось XY. В этом случае перпендикулярный вектор будет иметь координаты (0, 0, z), где z не равно нулю. Со знаком z нужно определиться. При построении проекций я исходил из того, что нахожусь с положительной стороны по оси Z, поэтому z > 0
Ориентация векторов определяется по знаку определителя, составленного из координат. Первую строку составляют координаты поворачиваемого вектора, вторую – вектора, к которому поворачивается первый и третью – вектор V. Для нашего случая (AE поворачивается до совпадения с AC) это

Поскольку мы определились, что z будет строго положителен, на знак результата его значение не повлияет

Т.е окончательный угол поворота для случая проекции на ось XY, это

Аналогично рассчитывается направление поворота для проекции на ось XZ
Ну и последнее замечание. Полностью независимо друг от друга углы поворота рассчитывать нельзя. Башня может сделать полный поворот (от -180 до 180 градусов) вокруг горизонтальной оси, но вокруг вертикальной это обычно невозможно (будет выглядеть, как будто пушка оторвалась от основы и перевернулась. Вертикальный поворот логично ограничить диапазоном от -90 до 90 градусов.
Реализовать это проще всего так.
1. Находим угол горизонтального поворота
2. Поворачиваем цель на этот угол вокруг оси горизонтального поворота в противоположном направлении
3. Рассчитываем вертикальный угол наведения для новых координат цели.
Или (что, по сути, то же самое) можно сначала поворачивать башню горизонтально, а потом рассчитывать угол вертикального поворота.
Теперь пушка будет попадать.