Комментарии 44
Я для сглаживания использую сплайн Акима, он более устойчив к выбросам.
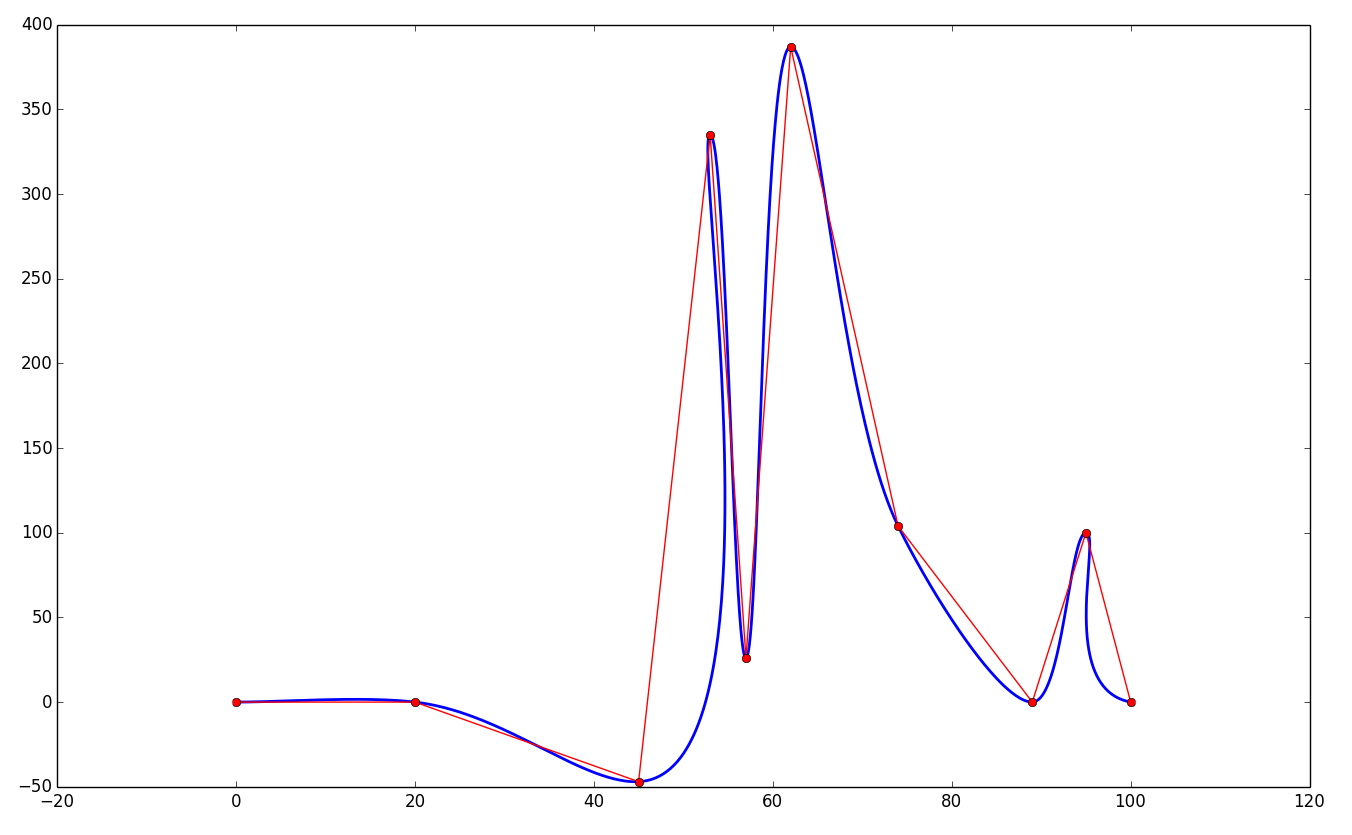
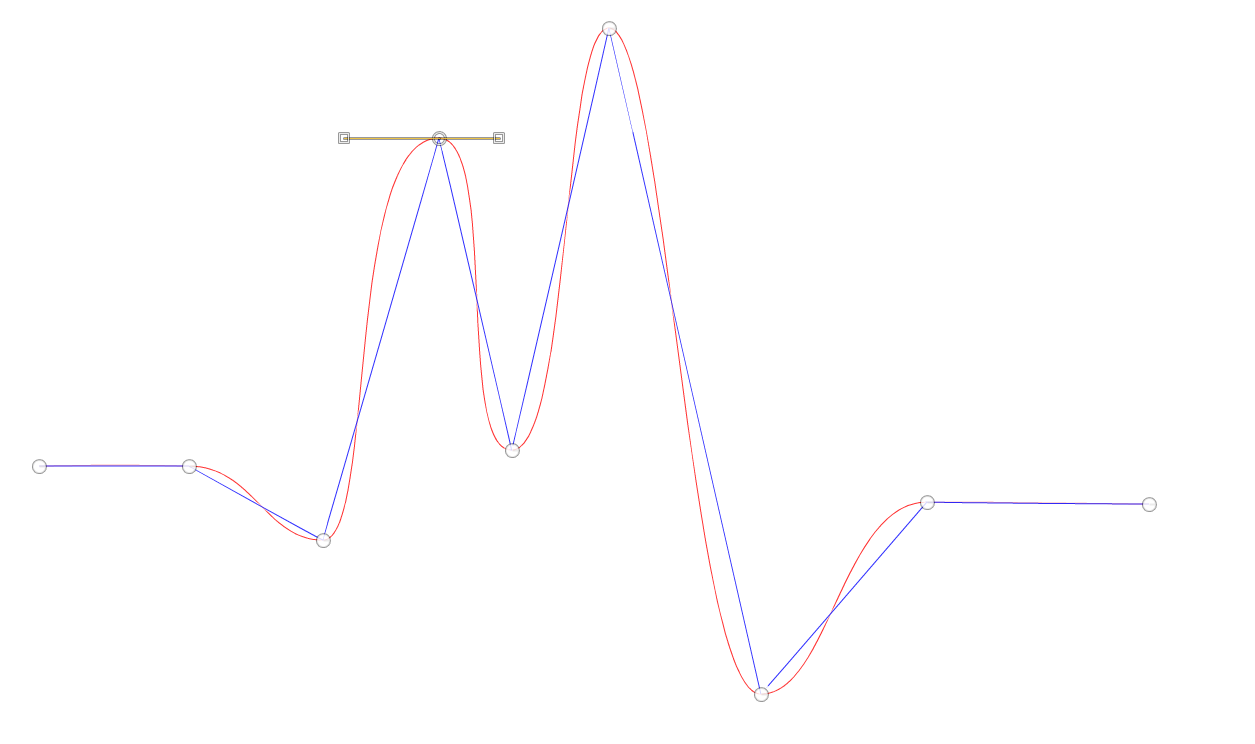
Более устойчив, да, но не безгрешен. По крайней мере, вот в этой реализации он явно «вспухает» на первом сегменте, ну и на пиках тоже — глобальный максимум составляет 388.018, хотя в данных это 387.0. Впрочем, наверное, и его можно отпатчить, чтобы косяков не было :)
Пруфпик (из кликабл, там хорошо видно косяки сверху):
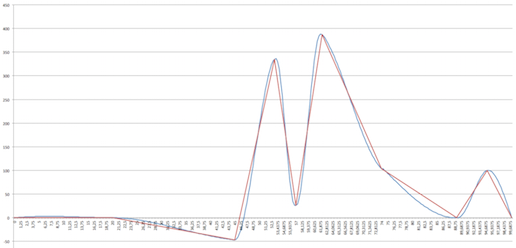
Пруфпик (из кликабл, там хорошо видно косяки сверху):

Не подскажите хорошее описание как его строить? А то сложно найти даже в спец. литературе.
Посмотрите код на Matlab: www.mathworks.com/matlabcentral/fileexchange/36800-interpolation-utilities/content/cakima.m
А вообще вот, информации довольно много: stackoverflow.com/a/4637884/419926
А вообще вот, информации довольно много: stackoverflow.com/a/4637884/419926
Откуда взялся такой странной полином Лагранжа при сравнении с линейной интерполяцией? Он же должен быть вырожденным, с нулевыми коэффициентами
Тыщу лет ждал такую статью. Я понимаю что вся эта информация есть в других источниках, но в заметке всё ближе к практике.
Ещё было бы интересно услышать, как растеризуется линия интерполирующего полинома.
Вот у нас есть параметр t в промежутке [0,1] и мы можем получать значения интерполирующей функции от этого параметра (x,y) = f(t).
Но как выбрать шаг изменения параметра, что бы закрасить все нужные пиксели?
Вот у нас есть параметр t в промежутке [0,1] и мы можем получать значения интерполирующей функции от этого параметра (x,y) = f(t).
Но как выбрать шаг изменения параметра, что бы закрасить все нужные пиксели?
Выбор шага — вопрос сложный, да :) По-хорошему, надо подобрать для текущего dpi некоторую длину аппроксимирующей линии и корректировать шаг так, чтобы эту длину не превышать. Но мы пока этот вопрос решили просто выносом параметра в публичный API. По умолчанию на один сегмент приходится 32 аппроксимирующих линии, а если результат пользователю не понравится (будут видны изломы), число линий можно увеличить.
Возможно, нужно для этого использовать идею Алгоритма Брезенхэма. Если «на пальцах», то результирующую кривую придется рисовать попиксельно, и для каждого пикселя определять из всех его соседей (соседей будет 7 штук, т.к. 8-й — это предыдущий пиксель) наиболее подходящий, у которого геометрический центр имеет наименьшее расхождение с аналитической кривой.
Шаг в 1 / max(|x'(t1)|, |y'(t1))|) достаточен, чтобы закрасить все нужные пиксели, кроме, возможно, точек где функция меняет направление и тех где функция резко «ускоряется».
Точки, где функция меняет направление, можно при желании закрасить отдельно, приравняв вторую производную каждой координаты нулю и решив это уравнение.
Точки, где функция «ускоряется», ловятся явной проверкой на «перепрыгивание» пикселя с уменьшением шага.
Но я с трудом представляю себе задачу, где нужна такая точность )
Точки, где функция меняет направление, можно при желании закрасить отдельно, приравняв вторую производную каждой координаты нулю и решив это уравнение.
Точки, где функция «ускоряется», ловятся явной проверкой на «перепрыгивание» пикселя с уменьшением шага.
Но я с трудом представляю себе задачу, где нужна такая точность )
Достаточно, чтобы шаг был приблизительно равен коэффициенту кривизны в данной точке, который для декартовых координат вычисляется так: 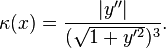 (или 1 / R, где R — радиус кривизны в данной точке).
(или 1 / R, где R — радиус кривизны в данной точке).
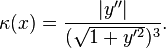 (или 1 / R, где R — радиус кривизны в данной точке).
(или 1 / R, где R — радиус кривизны в данной точке).Больше всего понравился вариант aChartEngine — по таким кривым хорошо текст рисовать и другие обводки.
Жаль в топике форум нет, надо будет исходники поковырять.
Жаль в топике форум нет, надо будет исходники поковырять.
Есть еще D3.js
Там есть хорошее решение интерполяции, которое называется monotone.
Там есть хорошее решение интерполяции, которое называется monotone.
Скрытый текст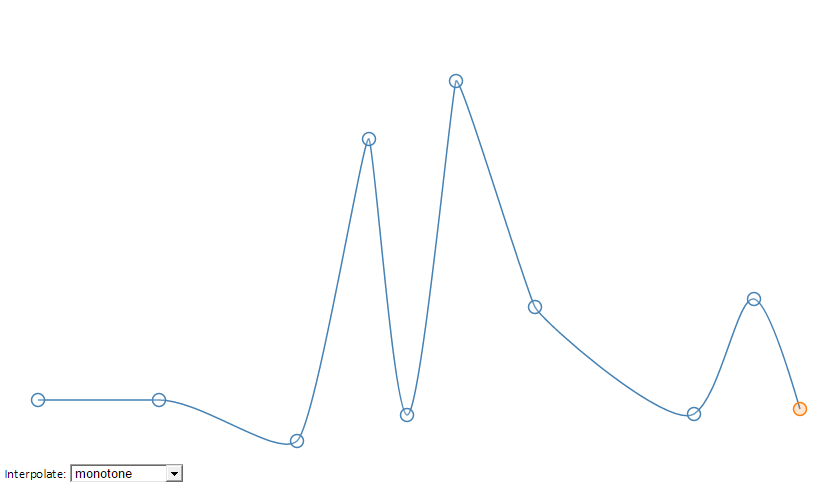

Пардон, ошибка закралась — вот правильная картинка:


Кстати, в примере про amCharts та же ошибка — шкала по оси Х на картинке не линейная
Она и у экселя с кальком не линейная :) Бог его знает, зачем они это делают.
Есть ещё такая штука как «Piecewise Cubic Hermite Interpolating Polynomial». Кусочно-полиномиальная интерполяция кубическими сплайнами Эрмита. Может дать лучшие результаты в некоторых случаях. Вот пример из Matlab: www.mathworks.com/help/matlab/ref/pchip.html
Можно еще посмотреть в сторону центростремительных сплайнов Catmull-Rom.
Чо-т с ними как-то печально получается:
Это вот прям код из той статьи в Википедии. Может, там что-то напутано с реализацией?

Это вот прям код из той статьи в Википедии. Может, там что-то напутано с реализацией?
Похоже, у вас в реализации где-то ошибка. Я писал когда-то реализацию на Matlab этих сплайнов для интерполяции 2D-кривых. Проверил на своей реализации, вроде всё правильно работает.
Вот мой код: gist.github.com/espdev/58e7189f5db573585304
Параметр tension определяет упругость сплайна. Чем он меньше, тем сплайн меньше выгибается.
Картинка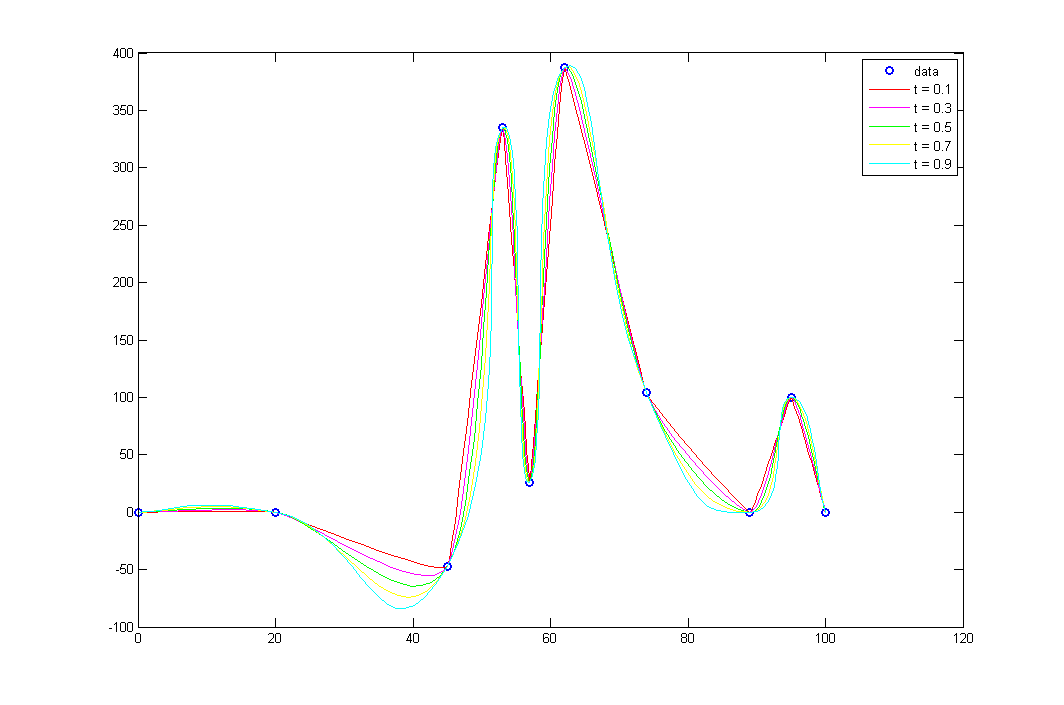

Вот мой код: gist.github.com/espdev/58e7189f5db573585304
Параметр tension определяет упругость сплайна. Чем он меньше, тем сплайн меньше выгибается.
А если просто Catmull-Rom? У них, по идее, таких сильных всплесков быть не должно.
therndguy.com/papers/curves.pdf
therndguy.com/papers/curves.pdf
А monotone в D3.js парой комментов выше — это не оно ли?
Расскажите, пожалуйста, как были выбраны точки для примеров (почти с потолка).
aChartEngine, вроде как самая популярная библиотека построения графиков для Android
Больше всего похоже на кривую Безье степени n – 1, хотя в самой библиотеке график называется «cubic line».
Поже на NURBS со степенью 2 и clamped knot вектором, где входные точки для интерполяции принимались за контрольные точки.
Вопрос, а почему мы считаем линейную интерполяцию идеальной? Такое ощущение, что мы её построили, а затем занимаемся тем, что пытаемся получить точно такую же, «но другую», более гладкую.
Ага, так и есть. Линейная интерполяция хороша тем, что она не так сильно вводит нас в заблуждение.
Но обычно ситуация развивается примерно так…
Разговор крутого спеца по data science и его начальника:
— У нас тут набор пар чисел есть, я накидал их на координатную плоскость, но есть одна проблемка: я понятия не имею, что происходит между ними. Поэтому я решил соединить их ломанной, чтобы можно было хоть проследить взглядом в какой последовательности на них смотреть.
— Молодец! Только вот выглядит это не круто и не убедительно, не похоже ведь на «красивую» функцию. Надо что-то с этим сделать.
— Нууу даа, согласен… Хм, а давайте тогда её сгладим, ну чтоб солиднее выглядела.
— Давай, попробуй.
Некоторое время спустя:
— Ну что, лучше стало?
— Ну вот, сразу бы так, теперь и в презентацию не стыдно вставить! И в фэйсбук с твиттером запостить можно.
P.S. Интерполяция штука полезная, главное понимать что за ней стоит. А статья была познавательная, спасибо автору.
Но обычно ситуация развивается примерно так…
Разговор крутого спеца по data science и его начальника:
— У нас тут набор пар чисел есть, я накидал их на координатную плоскость, но есть одна проблемка: я понятия не имею, что происходит между ними. Поэтому я решил соединить их ломанной, чтобы можно было хоть проследить взглядом в какой последовательности на них смотреть.
— Молодец! Только вот выглядит это не круто и не убедительно, не похоже ведь на «красивую» функцию. Надо что-то с этим сделать.
— Нууу даа, согласен… Хм, а давайте тогда её сгладим, ну чтоб солиднее выглядела.
— Давай, попробуй.
Некоторое время спустя:
— Ну что, лучше стало?
— Ну вот, сразу бы так, теперь и в презентацию не стыдно вставить! И в фэйсбук с твиттером запостить можно.
P.S. Интерполяция штука полезная, главное понимать что за ней стоит. А статья была познавательная, спасибо автору.
Ага, а потом оказывается, что нужно было интерполировать экспонентой по МНК.
Нужно понимать физический смысл рисуемых кривых, а так это пальцем в небо, график с КДПВ прекрасно иллюстрирует то же, что и остальные картинки, просто они сильнее это маскируют. Если график нужен для модной инфографики и не должен отображать хоть погоду на Марсе, лишь бы было прикольно — тогда ладно.
Нужно понимать физический смысл рисуемых кривых, а так это пальцем в небо, график с КДПВ прекрасно иллюстрирует то же, что и остальные картинки, просто они сильнее это маскируют. Если график нужен для модной инфографики и не должен отображать хоть погоду на Марсе, лишь бы было прикольно — тогда ладно.
интерполировать экспонентой по МНКЭто уже аппроксимация получается. :)
Интерполяцию часто применяют, чтобы напихать промежуточных точек если их не хватает, а аппроксимацию как раз для приближения функций и моделирования, нахождения неизвестных параметров.
Окей, согласен. Тогда такой вопрос — у вас в целом решение лучше получается, чем у экселей и ко или только на данных входных данных? А то есть мысль, что подогнали эвристики для конкретного случая, а в общем может оказаться большая ошибка по сравнению с тем же экселем.
Ну, это, наверное, вопрос всё же к авторам статьи.
Я думаю, что придумывать и подгонять эвристики под конкретные данные при интерполяции — это не очень хорошо. Лучше использовать кусочную интерполяцию известными сплайнами, для которых есть точное математическое определение. Тогда будет понятно, как интерполяция будет себя вести на любых данных.
Если же цель — найти закон и параметры модели для приближения данных, про которые вам что-то известно, то тут нет никаких ограничений, берёте регрессионный анализ и аппроксимируете чем угодно, хоть линейным МНК (если получается), хоть нелинейным с придуманной вами моделью (функцией).
Я думаю, что придумывать и подгонять эвристики под конкретные данные при интерполяции — это не очень хорошо. Лучше использовать кусочную интерполяцию известными сплайнами, для которых есть точное математическое определение. Тогда будет понятно, как интерполяция будет себя вести на любых данных.
Если же цель — найти закон и параметры модели для приближения данных, про которые вам что-то известно, то тут нет никаких ограничений, берёте регрессионный анализ и аппроксимируете чем угодно, хоть линейным МНК (если получается), хоть нелинейным с придуманной вами моделью (функцией).
Именно. Практика сглаживания вообще порочна в любых точных науках или инженерии.
Измеренные точки — это единственное, что вам достоверно известно о системе. Без знания или какого-то понимания процесса любая интерполяция обманчива, а иногда просто не допустима. Линейная в этом плане лучше всего, потому что она используется по умолчанию и не нужно уточнять модель и коэффициенты, используемые для сглаживания. Но красота требует плавных линий. По хорошему же надо отображать отдельно точки и отдельно линией регрессионную модель, которая не обязательно должна проходить по всем точкам.
У меня был смешной случай на эту тему — после выпуска очередного продукта дизайнер попросил у меня пару графиков для рекламной брошюры о продукте. Я ему выслал несколько графиков с точками и линейной интерполяцией для наглядности. Графики были временные, что важно. Он, я так понимаю, засунул это в какой-то редактор и скруглил. Прислал на утверждение — я смотрю, а там линия так скруглена, что изгибы дают местами по две одновременных точки в один момент времени. Такой вот кот Шрёдингера.
Измеренные точки — это единственное, что вам достоверно известно о системе. Без знания или какого-то понимания процесса любая интерполяция обманчива, а иногда просто не допустима. Линейная в этом плане лучше всего, потому что она используется по умолчанию и не нужно уточнять модель и коэффициенты, используемые для сглаживания. Но красота требует плавных линий. По хорошему же надо отображать отдельно точки и отдельно линией регрессионную модель, которая не обязательно должна проходить по всем точкам.
У меня был смешной случай на эту тему — после выпуска очередного продукта дизайнер попросил у меня пару графиков для рекламной брошюры о продукте. Я ему выслал несколько графиков с точками и линейной интерполяцией для наглядности. Графики были временные, что важно. Он, я так понимаю, засунул это в какой-то редактор и скруглил. Прислал на утверждение — я смотрю, а там линия так скруглена, что изгибы дают местами по две одновременных точки в один момент времени. Такой вот кот Шрёдингера.
интересно! :)
Анна, спасибо за познавательную статью и хорошо преподнесённый теоретический материал. Замечательная идея и очень интересный, с точки зрения математики, алгоритм. Однако, есть несколько «НО» из-за которых пришлось отказаться от реализации алгоритма в продакшн:
1. В коде есть серьёзные баги. О них дальше.
2. Отсутствие каких-либо комментариев сильно усложняет дебагинг. Это особенно относится к тем компонентам, которые формируют математический аппарат.
3. И… увы! Алгоритм формирует ложные экстремумы! Именно из-за этого пришлось от него полностью отказаться, несмотря на время, потраченное на поиск и устранение багов (
Итак, обещанные баги:
Сборка:
Сборка с дополнительными уровнями предупреждений заставляет поразмыслить над сообщениями, обещающими массу проблем на больших цифрах. Например:
Синтаксис:
abs() работает с целочисленными значениями. Компиллятор g++ догадывается и исправляет, но лучше использовать fabs()
Алгоритм:
1. Если использовать такой массив с данными (он идентичен исходному примеру, но без последней точки):
То появляются подобные артефакты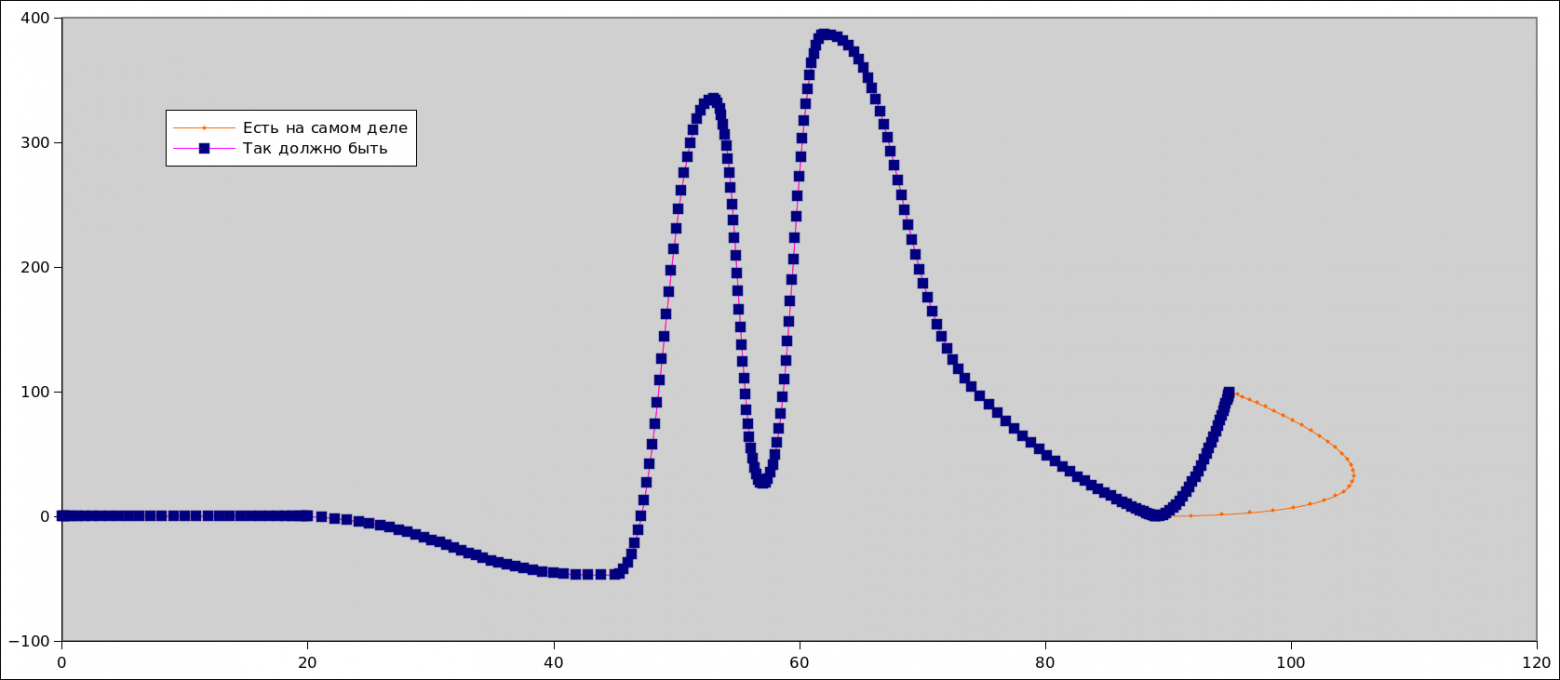
Вот маленький патч, устраняющий артефакты. Да, решение далеко от изящества, но, зато, работает:
2. Ложные экстремумы. Вот примеры наборов иксов с игреками, при которых их можно наблюдать.
Между 4 и 5 точками:
Между 7 и 8 точками:
Идентичное поведение интерполирующего алгоритма можно наблюдать и на других наборах данных, на которых кривая спускается, идёт горизонтально и снова поднимается.
Для тех, кто пожелает разобраться и исправить баг с ложными экстремумами добро пожаловать!
Код на гитхабе: https://github.com/eitijupaenoithoowohd/TBezierInterpolation
Помимо C++ добавлен код на чистом Си.
1. В коде есть серьёзные баги. О них дальше.
2. Отсутствие каких-либо комментариев сильно усложняет дебагинг. Это особенно относится к тем компонентам, которые формируют математический аппарат.
3. И… увы! Алгоритм формирует ложные экстремумы! Именно из-за этого пришлось от него полностью отказаться, несмотря на время, потраченное на поиск и устранение багов (
Итак, обещанные баги:
Сборка:
g++ -pipe -std=c++11 -g -ggdb -ggdb3 -O0 -DDEBUG -finline-functions -Wall -Wextra -Wpedantic -Wshadow -Wconversion -Wsign-conversion -Winit-self -Wunreachable-code -Wformat-y2k -Wformat-nonliteral -Wformat-security -Wmissing-include-dirs -Wswitch-default -Wtrigraphs -Wstrict-overflow=5 -Wfloat-equal -Wundef -Wshadow -Wcast-qual -Wcast-align -Wwrite-strings -Winline -Wsuggest-attribute=const -Wsuggest-attribute=pure -Wsuggest-attribute=noreturn -Wsuggest-attribute=format -Wmissing-format-attribute -Wlogical-op -o TBezierInterpolation TBezierInterpolation.cpp -lm
Сборка с дополнительными уровнями предупреждений заставляет поразмыслить над сообщениями, обещающими массу проблем на больших цифрах. Например:
warning: conversion to ‘int’ from ‘std::vector<Point2D>::size_type {aka long unsigned int}’ may alter its value
Синтаксис:
abs() работает с целочисленными значениями. Компиллятор g++ догадывается и исправляет, но лучше использовать fabs()
Алгоритм:
1. Если использовать такой массив с данными (он идентичен исходному примеру, но без последней точки):
testValues.push_back(Point2D(0, 0));
testValues.push_back(Point2D(20, 0));
testValues.push_back(Point2D(45, -47));
testValues.push_back(Point2D(53, 335));
testValues.push_back(Point2D(57, 26));
testValues.push_back(Point2D(62, 387));
testValues.push_back(Point2D(74, 104));
testValues.push_back(Point2D(89, 0));
testValues.push_back(Point2D(95, 100));
То появляются подобные артефакты

Вот маленький патч, устраняющий артефакты. Да, решение далеко от изящества, но, зато, работает:
--- TBezierInterpolation.cpp 2017-06-03 18:46:11.322309503 +0300
+++ TBezierInterpolation.cpp 2017-06-03 18:49:02.960312804 +0300
@@ -63,21 +63,26 @@
double l1, l2, tmp, x;
- --n;
for (int i = 0; i < n; ++i)
{
bezier[i].points[0] = bezier[i].points[1] = values[i];
bezier[i].points[2] = bezier[i].points[3] = values[i + 1];
- cur = next;
- next = values[i + 2] - values[i + 1];
- next.normalize();
-
tgL = tgR;
-
- tgR = cur + next;
- tgR.normalize();
+ cur = next;
+
+ if(i+1 < n){
+ next = values[i + 2] - values[i + 1];
+ next.normalize();
+
+ tgR = cur + next;
+ tgR.normalize();
+ }else{
+ tgR.x= 0.0;
+ tgR.y= 0.0;
+ }
+
if (abs(values[i + 1].y - values[i].y) < EPSILON)
{
@@ -120,12 +125,6 @@
bezier[i].points[2] -= tgR * l2;
}
- l1 = abs(tgL.x) > EPSILON ? (values[n + 1].x - values[n].x) / (2.0 * tgL.x) : 1.0;
-
- bezier[n].points[0] = bezier[n].points[1] = values[n];
- bezier[n].points[2] = bezier[n].points[3] = values[n + 1];
- bezier[n].points[1] += tgR * l1;
-
return true;
}
2. Ложные экстремумы. Вот примеры наборов иксов с игреками, при которых их можно наблюдать.
Между 4 и 5 точками:
39 -123,790531
54 -121,828107
81 -29,500421
111 -42,9229
158 -31,067327
170 0,077761
213 -61,771285
259 -75,374474
265 -90,913339
Между 7 и 8 точками:
124 50,435864
170 108,906317
171 159,643421
209 149,011485
254 214,373123
297 293,43677
310 206,841167
350 219,560966
388 221,341568
Идентичное поведение интерполирующего алгоритма можно наблюдать и на других наборах данных, на которых кривая спускается, идёт горизонтально и снова поднимается.
Для тех, кто пожелает разобраться и исправить баг с ложными экстремумами добро пожаловать!
Код на гитхабе: https://github.com/eitijupaenoithoowohd/TBezierInterpolation
Помимо C++ добавлен код на чистом Си.
Зарегистрируйтесь на Хабре, чтобы оставить комментарий

Интерполяция данных: соединяем точки так, чтобы было красиво