Пару лет назад я рассказывал жене сказки, что когда я буду старым маразматиком, мое ближайшее окружение не будет страдать от этого, ведь за мной будут ухаживать роботы. Новости о прогрессе искусственного интеллекта впечатляли меня (нейросетки то, нейросетки сё), свет в конце тоннеля манил, как и зарплаты специалистов в этой области. Разумеется, я не смог пройти мимо и решил погрузиться в Machine Learning.
Для старта хотелось почитать что-то совсем базовое, но поиск по строкам "машинное обучение для чайников" вменяемых результатов не дал. Все статьи начинались с тривиальных рассуждений, а потом перепрыгивали на загадочные формулы без особых пояснений. Я не сдавался и добыл несколько книг с хорошими отзывами, но получил то же самое, только уже на 600 страниц. Спустя полгода поисков могу сообщить вам следующее: при текущих темпах развития AI я не увижу роботов в старости, для работы с Machine Learning на самом деле не нужна математика, и как минимум одна статья "машинное обучение для чайников" существует, вы ее сейчас читаете.
Итак, ознакомившись с этой статьей вы поймете, что вообще представляет собой группа технологий ML. Имея эту базу вам будет проще двигаться дальше, и даже формулы в книгах станут понятнее. Раз уж зашел разговор о книгах, то сразу порекомендую ту, с которой у меня начался реальный прогресс: Andrew Glassner, "DEEP LEARNING: From Basics to Practice". В русском варианте она называется "Глубокое обучение без математики": автор разжевывает алгоритмы не прибегая к формулам. После томов, полных математического пафоса, это был просто глоток свежего воздуха. Еще один важный момент: постарайтесь читать англоязычную литературу, т.к. перевод терминов на русский язык местами сильно страдает. Человеку, который ввел фразу "Обучение с учителем" должно быть очень стыдно.
Создадим модель и обучим ее
Начнем с классики жанра: у нас есть база данных недвижимости с десятком атрибутов (стоимость, площадь, количество комнат и т.д.), на ее основе надо научиться предсказывать стоимость других домов. Тут вы скажете: "Стопэ! Нам надо нейросетку, которая убирает купальники с фотографий, а ты пихаешь нам примитивную задачу о расчете усредненной стоимости!". Я поначалу тоже был в шоке, что эти задачи являются существенной частью ML. И я пришел в ужас от того, что в ML распознавание объектов на фотографии работает по такому же принципу, что и наше предсказание стоимости. Тут ключевое слово "Работает", так что давайте продолжим, сейчас все станет понятно.
Задача сводится к двум шагам: выбрать модель (подобрать подходящую формулу расчета) и затем найти ее коэффициенты. Модель для нашего примера возьмем упрощенную:
Теперь мы будем перебирать значения коэффициентов A до тех пор, пока уровень ошибки не станет приемлемым, это и называется Обучением модели.
Ошибку каждый раз вычисляем, конечно же, по нашей базе данных (Обучающей выборке, Training Set), алгоритм очень простой: для каждого дома находим разницу между расчетной и фактической стоимостью, возводим разницу в квадрат (чтобы избавиться от отрицательных чисел) и находим среднее значение всех этих отклонений. Формула для вычисления ошибки называется Функцией потерь (Loss Function), описанный алгоритм расчета популярный, но не единственный.
Если ошибку не удается снизить до вменяемых значений, значит мы неудачно выбрали модель: возможно, надо количество комнат брать в квадрат, или Удаленность от центра не плюсовать, а делить. Вариантов много, математики не могут ответить на вопрос "Как выбрать модель", поэтому просто сидим и пробуем разные, пока не получится (тут становятся понятны некоторые шутки про Data Scientist-ов).
А что насчет распознавания объектов на фотографиях? Идея простая: если сделать огромную формулу, которая на вход принимает миллион значений (пиксели фотографии) и внутри имеет сотню тысяч коэффициентов, то после удачного "обучения" она начнет на выходе выдавать "Вероятность наличия собаки на фото" (значение от 0.0 до 1.0). И это прокатило, такие формулы действительно работают, это называют Глубоким обучением (Deep Learning). Есть две сложности: формулу такого размера руками не написать, а ее коэффициенты даже на супер-компьютере методом простого перебора не вычислить. Приступаем к оптимизации.
Перцептрон и Нейронная сеть
Если нужна очень большая формула с простой повторяющейся структурой, то самое логичное - это написать простенький скрипт по генерации исходного кода. К сожалению, нашим предкам в далекие 60-ые прошлого века эти инструменты были недоступны, да и заправляли тогда не программисты, а математики, поэтому был придуман Перцептрон.
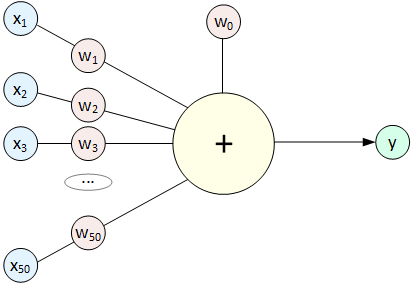
В книгах вы прочитаете, что идея создания Перцептрона была навеяна структурой нашего мозга (нейронами), но сходство там очень отдаленное. Перцептрон работает гораздо проще, это всего лишь графическое представление обычного линейного уравнения:
Обозначения: x - входные значения (параметры дома, пикселы и т.д.), w - коэффициенты модели, которые принято называть "Веса" (Weights), коэффициент w0 особый, его называют Смещением (Bias) и часто не отображают на схемах. Математики любят линейные уравнения, потому что они могут записать их в очень краткой форме - в виде перемножения матриц:
Всего одной строкой мы рассчитали стоимости всех домов в нашей базе: в одномерный массив W закидываем все веса перцептрона, в двумерный массив X помещаем всю базу недвижимости (кроме стоимости), а в выходном одномерном массиве Y получаем все рассчитанные стоимости. Но краткостью записи все достоинства матриц и заканчиваются. С вычислительной точки зрения здесь нет никакого ускорения (если вы конечно пишите не на Python), а сама операция сведется к трем вложенным циклам с расчетом все того же линейного уравнения. Отказ от матриц, напротив, дает больше пространства для маневра и оптимизаций, но это повод для отдельной статьи.
На практике вам не придется работать с матрицами, готовые библиотеки избавят вас от этой мороки, так что кроме как в книгах вы эти матричные формулы больше нигде не увидите (ну еще в статьях на Хабре).
На одном линейном уравнении далеко не уедешь, пока что наша модель не сможет корректно предсказать стоимость, не говоря уже о собаке на фото:
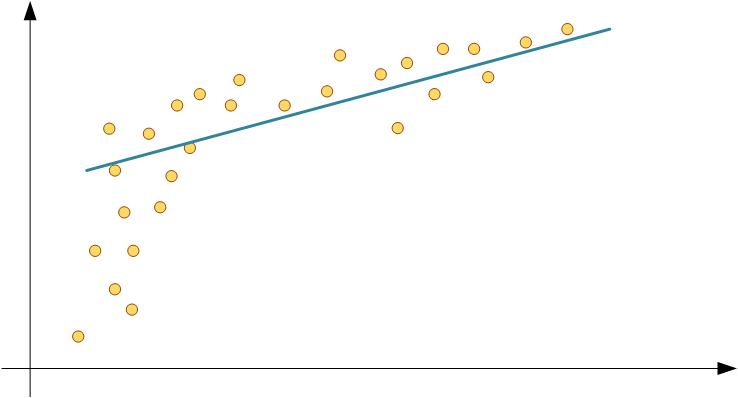
Точками отмечены данные из обучающей выборки, линия - результат моделирования. Не зависимо от количества весов, перцептрон остается просто линией. Чтобы получить кривую, необходимо добавить в модель что-нибудь нелинейное: синусы/косинусы, экспоненты, операции деления и возведения в степень.
Для большей гибкости перцептроны объединяют в нейронные сети (на таких рисунках не показывают Веса, но свой набор есть у каждого перцептрона в сети):
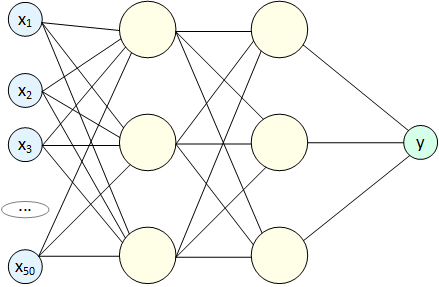
Тут нас ждет сюрприз: какие бы сложные комбинации связей мы ни рисовали, в итоге получим наше исходное линейное уравнение. Ни одно из входных значений x не будет возведено в степень, т.к. перцептроны соединяются между собой через операцию Сложения. Чтобы как-то исправить ситуацию на выходе каждого перцептрона добавили Функцию активации (Activation function):
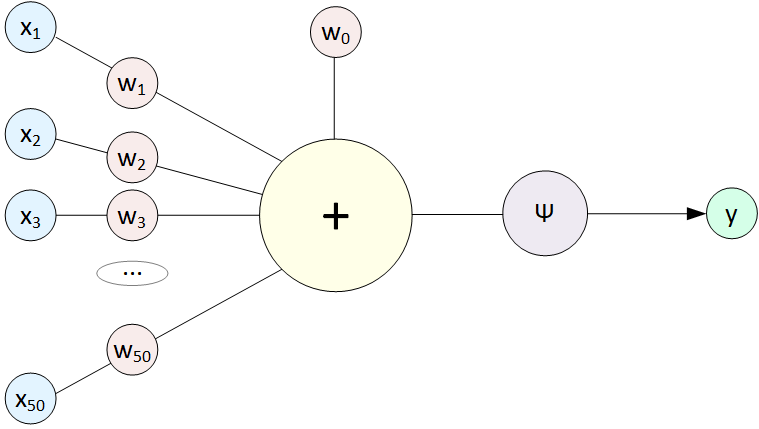
Эта функция Ψ обязательно нелинейная, конечно же есть популярные варианты, которые вы найдете в любой книге (рисунки с Wikipedia):
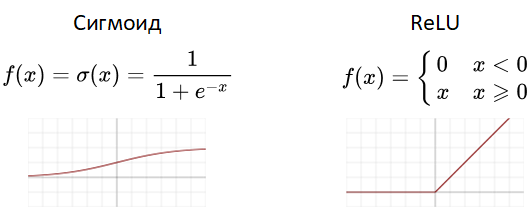
Какую функцию использовать в вашей модели? Математики также не могут ответить на этот вопрос, пробуйте разные и смотрите что лучше работает в вашем случае. Сигмоид относительно требователен к вычислительным ресурсам, поэтому его чаще ставят только на выходе нейросети, чтобы получить красивое значение от 0.0 до 1.0 (именно для красоты, на выходе он не влияет на работу сети). Говорят, что и обычный Косинус работает неплохо (если таки углубиться в математику и взглянуть на Ряд Фурье, то возникает ощущение, что именно им и надо пользоваться, но я сам пока не пробовал). Для полного понимания работы функций активации давайте взглянем, во что превратилось уравнение нашего перцептрона в случае Сигмоида:
Наша модель выглядит сложнее, а если попытаться нарисовать формулу для всей нейронной сети, то будет вообще мясо, даже в матричном виде ее уже не пытаются изобразить. Благодаря функциям активации гибкость достигнута.
Как разработчику, вам не потребуется прописывать все эти формулы, готовые библиотеки избавят вас и от этой мороки. Есть теорема, которая доказывает, что с помощью линейных уравнений с функциями активации можно смоделировать любой процесс. Теорема правда не говорит, сколько весов должно быть в модели и как долго вы ее будете обучать.
Обучение модели
Простой перебор весов займет очень длительное время, т.к. после любой их корректировки надо прогонять через нейронную сеть всю обучающую выборку, чтобы посмотреть, как изменилась ошибка. Здесь нам помогут два метода: Градиентный спуск (Gradient Descent) и в дополнение к нему Обратное распространение (Backpropagation). Детальное вменяемое описание работы этой пары вы найдете все в той же книге "DEEP LEARNING: From Basics to Practice", а я приведу только самую суть.
Шаг 1: после создания нейронной сети проставляем начальные значения всем весам (обычно, маленькие случайные числа), прогоняем через нее обучающую выборку и вычисляем ошибку (Loss function). Если ошибка равна нулю, то Бог есть и он сегодня с вами. Все остальные пройдемте к шагу два.
Шаг 2: теперь нам надо поправить веса так, чтобы ошибка стала меньше. Взглянем, например, на вес W508, в какую сторону будем его двигать?
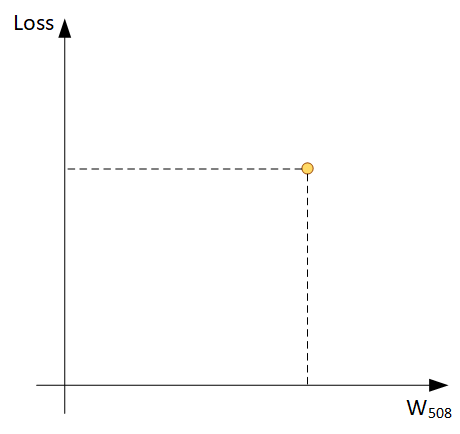
Теоретически, можно построить график зависимости Loss и W508, и выбрать минимальное значение, но это очень затратная процедура (это будет простой перебор всех значений W508). Однако, мы можем относительно дешево найти угол наклона такого графика в конкретной точке - Градиент.
Для этого нам требуется производная от Функции потерь, что уже требует знаний математики (кажется 11 класс школы), но вас это не должно беспокоить, все производные для стандартных Функций потерь уже найдены и заботливо упакованы в библиотеки. Вам требуется только общее понимание, как это работает, чтобы суметь разобраться в причинах сбоев при обучении.
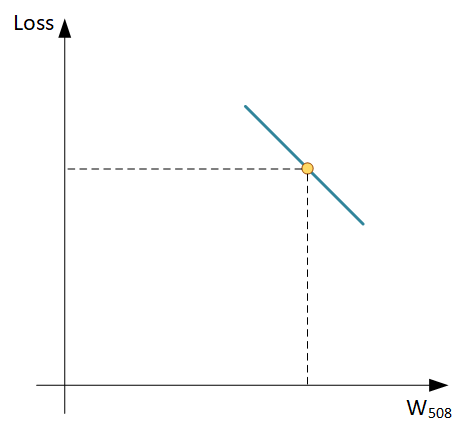
По градиенту мы видим не только в какую сторону менять вес, но и как сильно это делать (по крутизне наклона). По этой методике поочередно находим градиент для каждого веса и меняем их значения, это и есть Метод градиентного спуска.
Шаг 3: опять прогоняем обучающую выборку через сеть, вычисляем ошибку, вычисляем новые градиенты для весов:
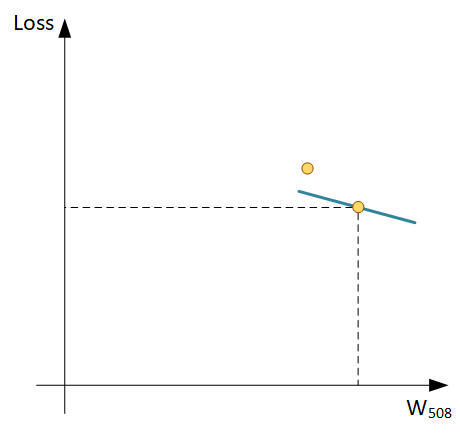
И видим прогресс: ошибка действительно изменилась в меньшую сторону, а новый Градиент имеет меньший угол наклона, значит мы близки к минимальному значению ошибки на графике. Повторяем процесс до посинения тех пор, пока модель не перестанет обучаться, в этом случае градиенты станут почти горизонтальными линиями.
Какие есть подводные камни? А давайте все-таки построим полный график для Веса W508
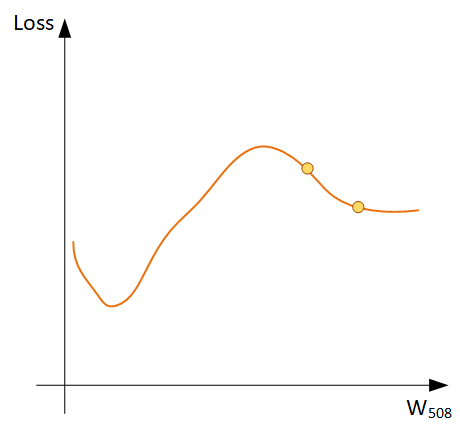
Оказывается, мы шли не в том направлении, потому что начальное значение веса (случайное число) упало не в ту часть графика. Мы достигли, так называемого, локального минимума, и на графике их может быть очень много. Как с этим бороться? Запускаем обучение заново и надеемся, что в этот раз исходное случайное значение веса упадет в нужную область. Метод проб и ошибок все еще наш лучший друг.
А что там с Backpropagation? Вроде все посчитали, все работает, он нам зачем? Вычисление градиента для каждого из весов, описанное выше, относительно затратная процедура. Метод обратного распространения сильно упрощает этот процесс: зная градиент для правой части нейронной сети мы легко вычисляем градиенты для весов, находящихся левее. Двигаясь по сети все левее и левее мы постепенно обновляем все веса. Из-за этого движения справа налево метод и назвали "Обратным".
Таким образом, Backpropagation занимается только вычислением градиентов, а обновление весов по найденным градиентам выполняется с помощью Метода градиентного спуска. В реальной жизни часто упоминают только Backpropagation, опуская вторую составляющую, но вы должны понимать, что они идут в паре.
Как работает Backpropagation? При попытке объяснить метод авторы очень любят погружаться в матричные вычисления, что напрочь убивает его понимание. Если вы его не осилите - не страшно, от программиста требуется только вызвать метод fit и знать, как работают дополнительные оптимизации, которые вы найдете в литературе.
Виды нейронных сетей
Выше уже был показан вариант Полносвязной нейронной сети (Fully connected neural network), но они бывают еще и такими:
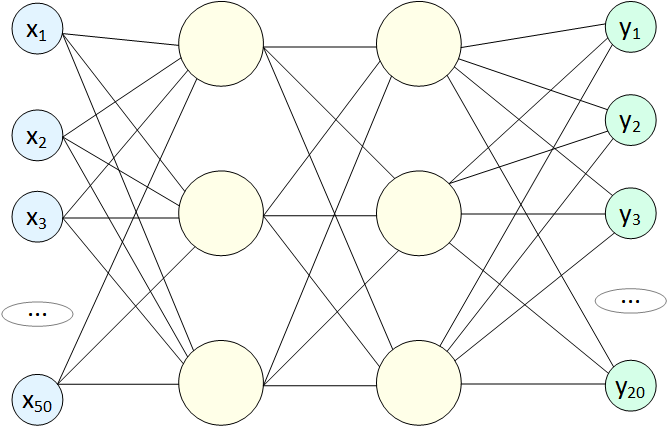
Здесь мы видим множество выходных значений. Такая сеть используется, например, в задачах классификации: на вход подаем пиксели картинки, на выходе получаем 20 чисел: y1 - вероятность, что на фото есть собака, y2 - кошка, и т.д. Одна нейронная сеть может распознавать тысячи объектов, но и сама она при этом становится объемнее (больше перцептронов, больше связей и весов). Также немного позже мы увидим, что сети с большим количеством выходов используются для генерации контента: на вход подаем несколько чисел, а на выходе получаем миллион значений - пиксели для картинки.
Кстати о картинках: в Полносвязную сеть пиксели изображения подаются построчно:
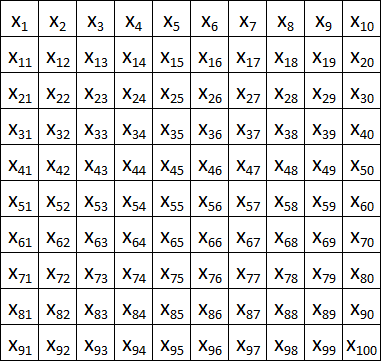
Это не очень-то логично, гораздо лучше близлежащие пиксели отправлять в нейросеть также рядышком:
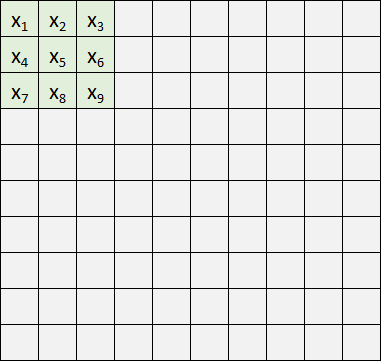
Так и появились Сверточные нейронные сети (Convolutional neural network), или просто CNN. Это все еще набор перцептронов с функциями активации внутри, но набор связей между ними специфический, уже не все со всеми. Обучаются они все тем же методом Backpropagation.
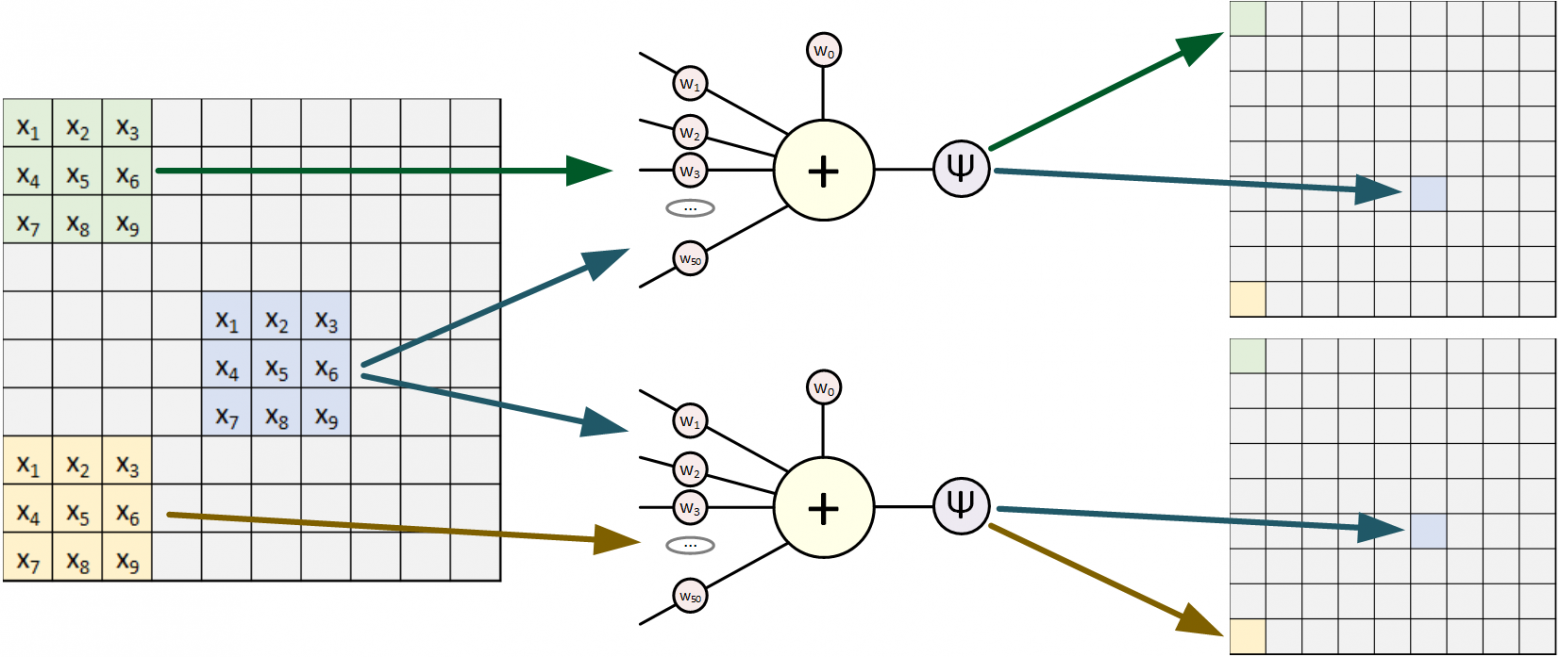
Выделенную на рисунке цветом область называют "Фильтр". Обычно это квадрат со стороной 3-5 пикселей. Фильтр накладывают на изображение: значения x умножаем на веса и суммируем их, т.е. пропускаем значения через перцептрон. Результат сохраняем в новый двумерный массив. Далее снова накладываем этот же фильтр на изображение, но уже сдвинув его вправо на один пиксель (иногда используют большее смещение), и так пробегаем по всему изображению. Все это повторяем с другими фильтрами (еще несколько перцептронов с другими значениями весов), сохраняя результаты в отдельные массивы. Отфильтрованные изображения прогоняем еще через несколько фильтров, подвергаем дополнительным обработкам, и результат можно, например, подать на полносвязную сеть.

Эти сети работают неплохо: даже если повернуть изображение на 180 градусов, сеть все равно найдет на ней собаку. Но именно этот эффект создает проблемы в задачах распознавания текстов. Изменение порядка слов в предложении может повлиять на его смысл, но полносвязная сеть и CNN не почувствуют разницы. Вот мы и подошли к третьему важному виду сетей - Рекуррентные нейронные сети (Recurrent neural networks ) или RNN.
В литературе их часто называют нейросетями с памятью, но так можно сказать с очень большой натяжкой. Также в учебниках вы часто увидите попытку объяснить работу RNN через графы, но можно не забивать себе этим голову. Работают они очень просто:
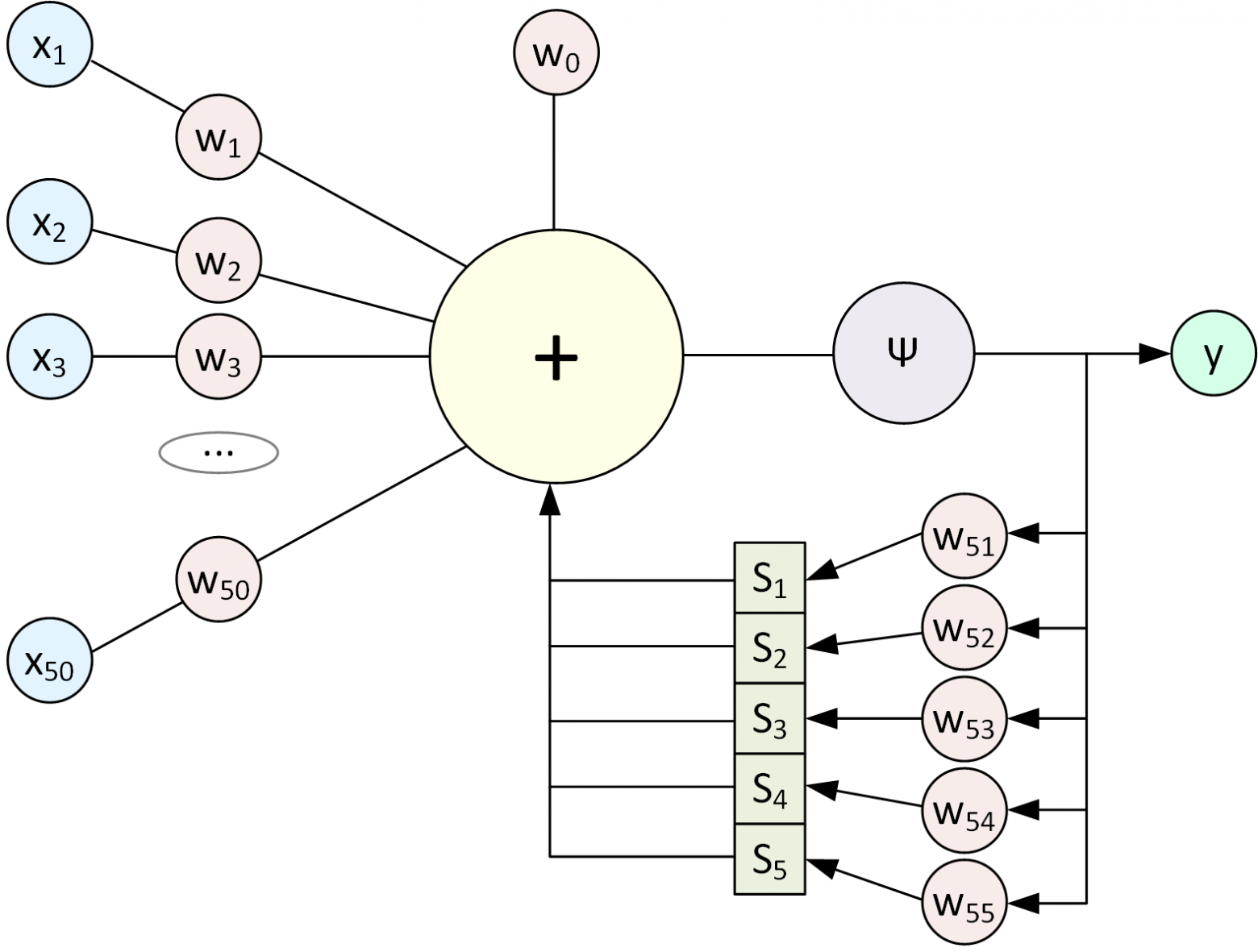
В перцептрон добавилось Состояние (массив S): это переменные, в которых мы сохраняем результат вычисления всего перцептрона (домножив на веса), чтобы использовать их при следующем вызове перцептрона. При первом запуске Состояние заполняется нулями. Если вы уже распознали какой-то блок текста (например, e-mail) и готовы перейти к следующему независимому блоку данных, то Состояние принудительно обнуляется.
Если вы пытаетесь предсказать температуру на завтра, то такая нейросеть будет оперировать не только текущими показаниями (облачность, сила и направление ветра), но и предыдущим значением температуры, что очень логично.
Для Состояния есть несколько усложнений, которые повышают качество работы RNN. Если мы хотим учитывать не только последнее выходное значение, но и несколько предыдущих, то формула вычисления Состояния немного меняется (исходный код, не математическая формула):
Таким образом мы не полностью перезаписываем значение, а добавляем некоторое изменение, в зависимости от выходного значения.
Гораздо более продвинутая сеть - LSTM (Long Short-Term Memory, Длительная краткосрочная память). Не будем пытаться понять ее название, перейдем сразу к сути: это все еще RNN, но с более сложным управлением Состояния. Перцептрон LSTM может внезапно обнулить свое Состояние (Забыть состояние), может отработать как обычная RNN (Запомнить состояние), и может какое-нибудь из Состояний внезапно не подать для вычислений (Выбрать состояние). Данное поведение управляется дополнительными весами. Обучение RNN и ее подвидов (LSTM) выполняется старым добрым Backpropagation.
Решаемые задачи
Алгоритмы машинного обучения подразделяют на "Обучение с учителем" (Supervised Learning, привет переводчику) и "Обучение без учителя" (Unsupervised Learning). Года два назад я был уверен, что речь идет о самообучаемых алгоритмах и о тех, за которыми надо присматривать. На самом деле здесь идет речь о двух группах:
Supervised - для которых нужны заранее размеченные данные в обучающих выборках (подписать картинки, есть там собака или нет, проставить стоимость для каждого дома и т.д.);
Unsupervised - для которых разметка не требуется (Кластеризация, Понижение размерности), о них чуть ниже.
Рассмотрим сами алгоритмы, начнем с Классификации, выше уже был пример: что находится на фото (кошка, собака и т.д.)? Другие классические примеры: является ли письмо спамом (бинарная классификация, т.к. ответ да/нет), распознавание букв и цифр на изображениях.
Регрессия: в самом начале статьи была задача "определение стоимости недвижимости" - это вот оно. По каким-то исходным данным мы выводим новые цифры. Предсказание температуры на завтра - аналогично.
Генерация контента, можно выполнить с помощью Автокодировщика. Для этого используется специфическая нейронная сеть с "бутылочным горлышком":
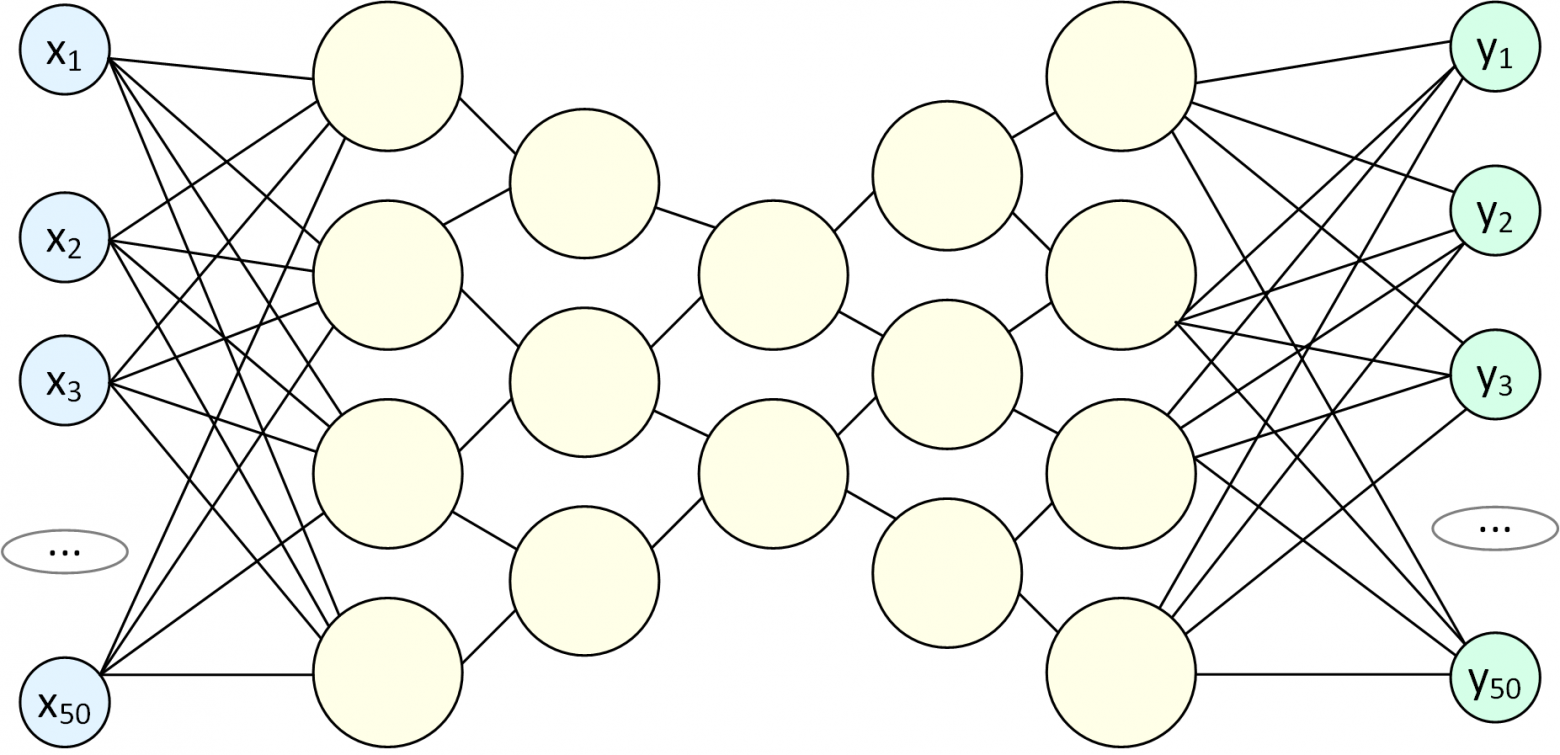
При обучении такую сеть заставляют на выходе генерировать точно такие же данные, что поступили на вход, например, в обучающую выборку включают разные фото травы. После завершения обучения сеть разрывают:
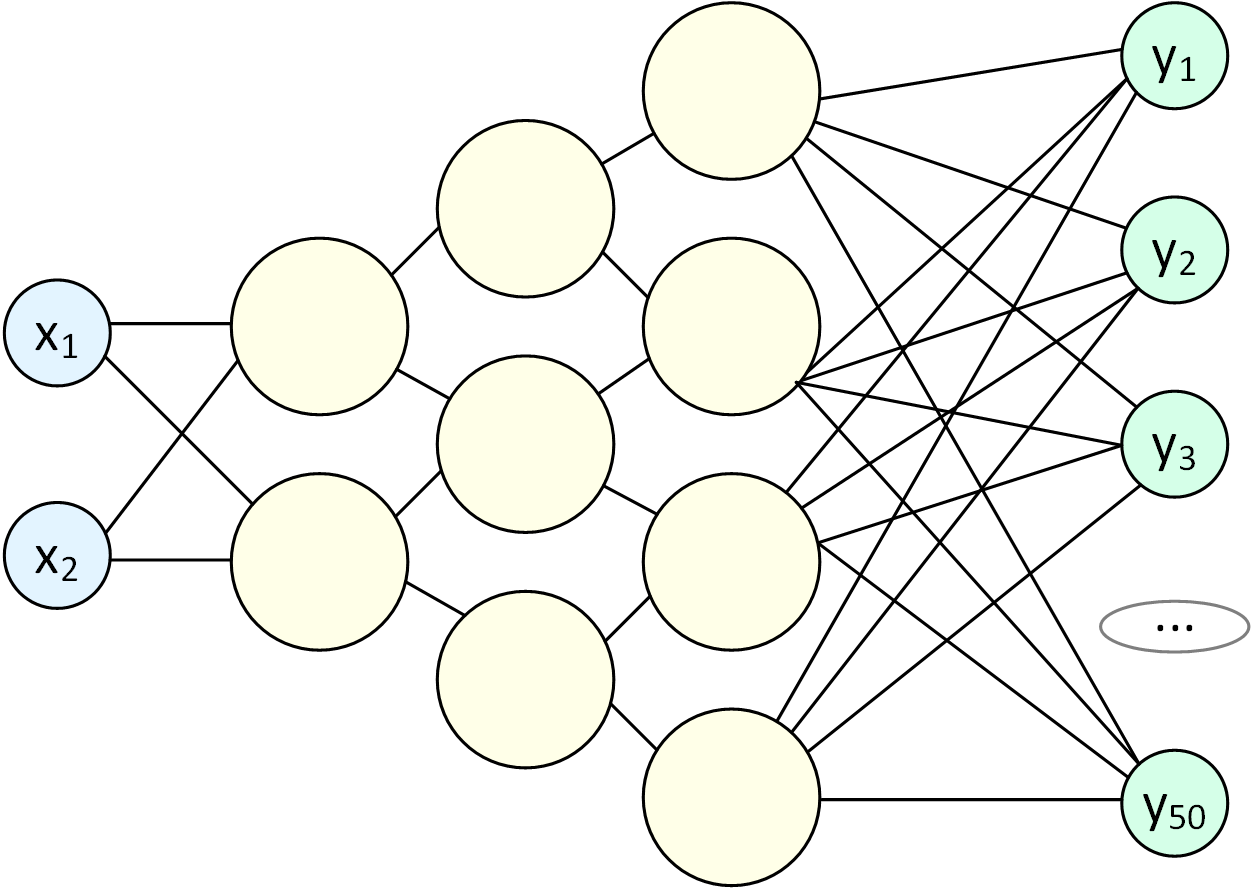
Теперь, подавая на вход пару чисел, на выходе мы можем получить совершенно новые изображения травы (либо белеберду, как повезет). Внутри Автокодировщика можно использовать полносвязные сети, CNN и RNN, а также любые их комбинации, важно только создать бутылочное горлышко.
Более современный способ генерации контента - Генеративно-состязательная сеть (Generative adversarial network, GAN). В этом случае обучаются две нейросети: первая учится распознавать контент, а вторая его генерировать. В процессе обучения выход второй сети на каждом шаге скармливают первой. После обучения для генерации используется только вторая сеть.
Нейросети можно также использовать для модификации контента: в обучающей выборке на вход подаем исходное изображение, на выход - требуемое. Если обучение прошло успешно, нейросеть будет выполнять аналогичные модификации для других изображений.
Кластеризация: задача алгоритма - сгруппировать данные, анализируя похожесть их атрибутов, например, разбить базу недвижимости на 3 группы. На старте алгоритма вы задаете только количество групп, что в них войдет - алгоритм решит сам. Этот алгоритм не использует нейросети: как я писал в самом начале, Machine Learning - это группа алгоритмов.
Понижение размерности: задача алгоритма - из большого количества атрибутов сделать чуть меньшее их количество. В принципе, примерно то же самое делает Автокодировщик на уровне своего бутылочного горлышка, но есть и популярный алгоритм без нейросетей: Метод главных компонент (Principal component analysis, PCA). Алгоритмы в том числе активно используются при обработке текстов.
За что же платят так много денег?
Как мы увидели выше, ничего особо сложного в Машинном обучении нет. Вся математика скрыта в недрах библиотек, количество алгоритмов ограничено, вариантов оптимизации не слишком много, сиди да подбирай коэффициенты случайным образом. Почему же зарплаты Data Scientist так высоки? Чтобы быть успешным в этом деле надо все-таки включать голову.
Успех складывается из двух вещей:
у вас есть очень много данных в обучающей выборке и очень мощные серверы для их обработки (тогда достаточно взять готовую GPT-3 и обучить ее русскому языку);
вы отлично знаете предметную область, в которой пытаетесь применить машинное обучение.
Меняя количество перцептронов в нейронной сети вы можете немного повысить качество ее работы, но настоящий прорыв возможен, если вы усовершенствуете алгоритм в целом. Например, декомпозируете задачу: с помощью первой нейронной сети преобразуем фотографию в простейшие фигуры (треугольник, круг, волнистые линии), а второй нейронкой определяем, что же там нарисовано.

Разработчики DeepMind достигли отличного результата с AlphaFold 2 вовсе не потому, что им повезло с обучением нейросети: они погрузились в задачу полностью и используют нейросеть лишь как часть алгоритма. Разберитесь с вашими данными - будет прорыв и у вас.
Заключение
В этой статье я привел лишь самые базовые вещи. Есть еще огромное количество нюансов, которые вы почерпнете из книг и статей, но у вас теперь есть основной вектор движения.
В самом начале я писал, что при текущих темпах развития AI разумных роботов я в старости не дождусь. Так ли это? Нейросеть - это всего лишь большая функция, которая ищет скрытые зависимости, она не может мыслить. Когда мы распознаем собаку на фотографии, здесь все просто: в обучающей выборке для фотографии подписываем "Собака" и запускаем обучение. Но если у нас есть просто слово "Собака", то что подписать под этим словом для обучения нейросети? "Собака"? Об этом мы поговорим в следующей статье - Создаем Сильный AI. Конкретика.