В работе служб МЧС и спасателей, которые устраняют последствия стихийного бедствия иди техногенной катастрофы критически важный фактор — надёжная связь. Но иногда катастрофы происходят в чрезвычайно удалённой местности, где работают только спутниковые телефоны. Как поднять нормальную сеть для всей группы?

Лаборатория саморегулирующихся систем в Политехническом институте Лозанны разработала проект SMAVNET (The Swarming Micro Air Vehicle Network), который должен решить эту проблему. Они предлагают использовать роевую сеть из десяти беспилотных летательных аппаратов, которые в считанные минуты организуют беспроводную сеть на обширной территории. Достаточно бросить их в воздух (видеосъёмка процесса развёртывания сети под хабракатом).

Лаборатория саморегулирующихся систем в Политехническом институте Лозанны разработала проект SMAVNET (The Swarming Micro Air Vehicle Network), который должен решить эту проблему. Они предлагают использовать роевую сеть из десяти беспилотных летательных аппаратов, которые в считанные минуты организуют беспроводную сеть на обширной территории. Достаточно бросить их в воздух (видеосъёмка процесса развёртывания сети под хабракатом).

 Перед тем как начать переносить реализацию вычислительного алгоритма на видеокарту стоит задуматься — получим ли мы желаемый прирост производительности или только потеряем время. И несмотря на обещания производителей о сотнях GFLOPS, у современного поколения карт есть свои проблемы, о которых лучше знать заранее. Я не буду глубоко уходить в теорию и рассмотрю несколько существенных практических моментов и сформулирую некоторые полезные выводы.
Перед тем как начать переносить реализацию вычислительного алгоритма на видеокарту стоит задуматься — получим ли мы желаемый прирост производительности или только потеряем время. И несмотря на обещания производителей о сотнях GFLOPS, у современного поколения карт есть свои проблемы, о которых лучше знать заранее. Я не буду глубоко уходить в теорию и рассмотрю несколько существенных практических моментов и сформулирую некоторые полезные выводы.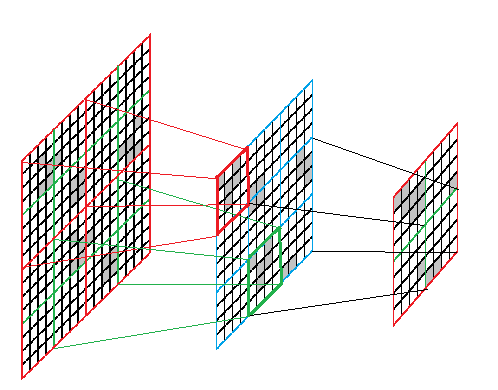
 Отличный способ освоить Python —
Отличный способ освоить Python —