Всем привет. Меня зовут Артур. Готовясь к выступлению на внутреннем митапе по теме особенности алгоритмов у CatBoost и LightGBM, я понял, что не смог найти единого места, где были бы понятным языком рассказаны основные особенности того, что алгоритмически работает под капотом у CatBoost и LightGBM. Причём не формальные записи алгоритмов на псевдокоде, а понятные пошаговые инструкции. Так появилась эта статья.

Всем привет! Недавно я на практике применил одно интересное решение, которое давно хотел попробовать, и теперь готов рассказать, как своими руками такое можно сделать для любой другой аналогичной задачи. Речь пойдет о создании своей кастомизированной версии ChatGPT, которая отвечает на вопросы, учитывая большую базу знаний, которая по длине не ограничивается размером промта (то есть вы бы не смогли просто добавить всю информацию перед каждым вопросом к ChatGPT). Для этого будем использовать контекстные эмбеддинги от OpenAI (для действительно качественного поиска релеватных вопросов из базы знаний) и сам СhatGPT API (для оборачивания ответов в натуральный человеческие ответы). При этом, также предполагается, что ассистент может отвечать не только на прямо указанные в Q&A вопросы, но и на такие вопросы, на которые смог бы отвечать человек, который ознакомился с Q&A. Кому интересно научиться делать простых ботов, отвечающих по большой базе знаний, добро пожаловать под кат.

Привет, Хабр!

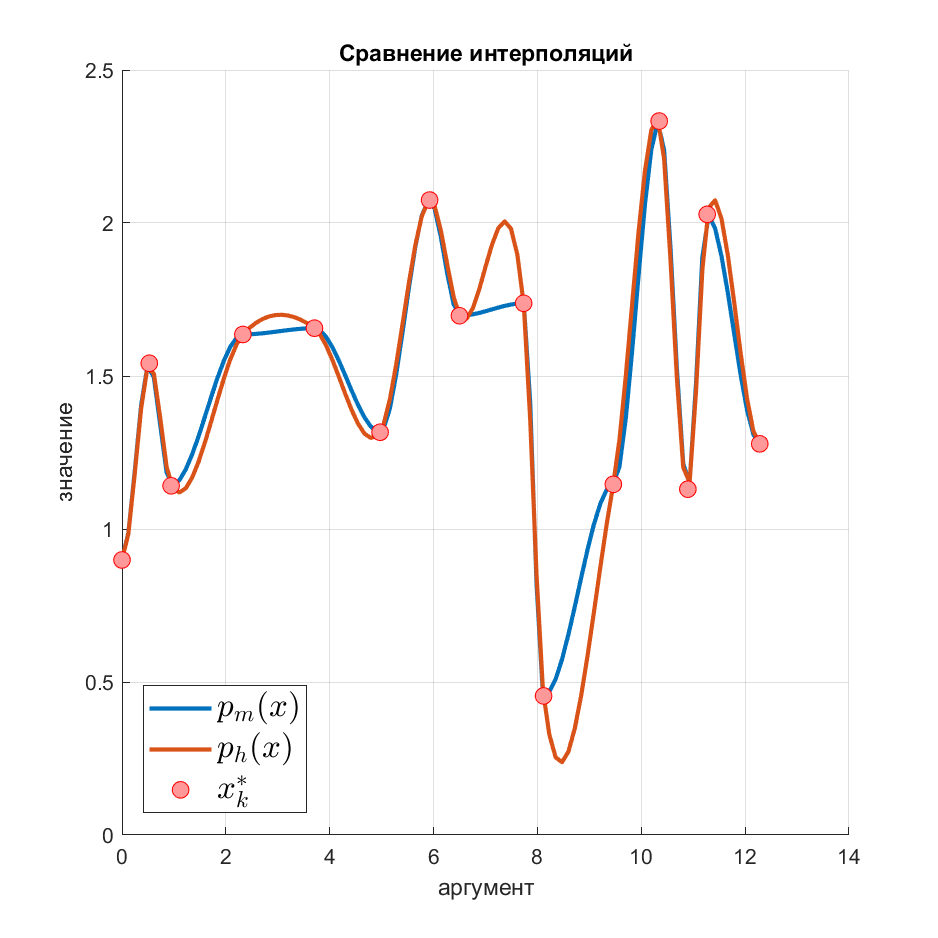
В данной статье разобран алгоритм монотонной кубической интерполяции, предложенный Фритчем и Карлосоном в работе [1].

На рисунке красным обозначен результат обычной кубической интерполяции Эрмита, а синим - монотонной, кругами - опорные точки траектории.

Примеры кода написаны на C++, исходники всей библиотеки лежат здесь. Также написана копия библиотеки на Java, исходники лежат здесь.

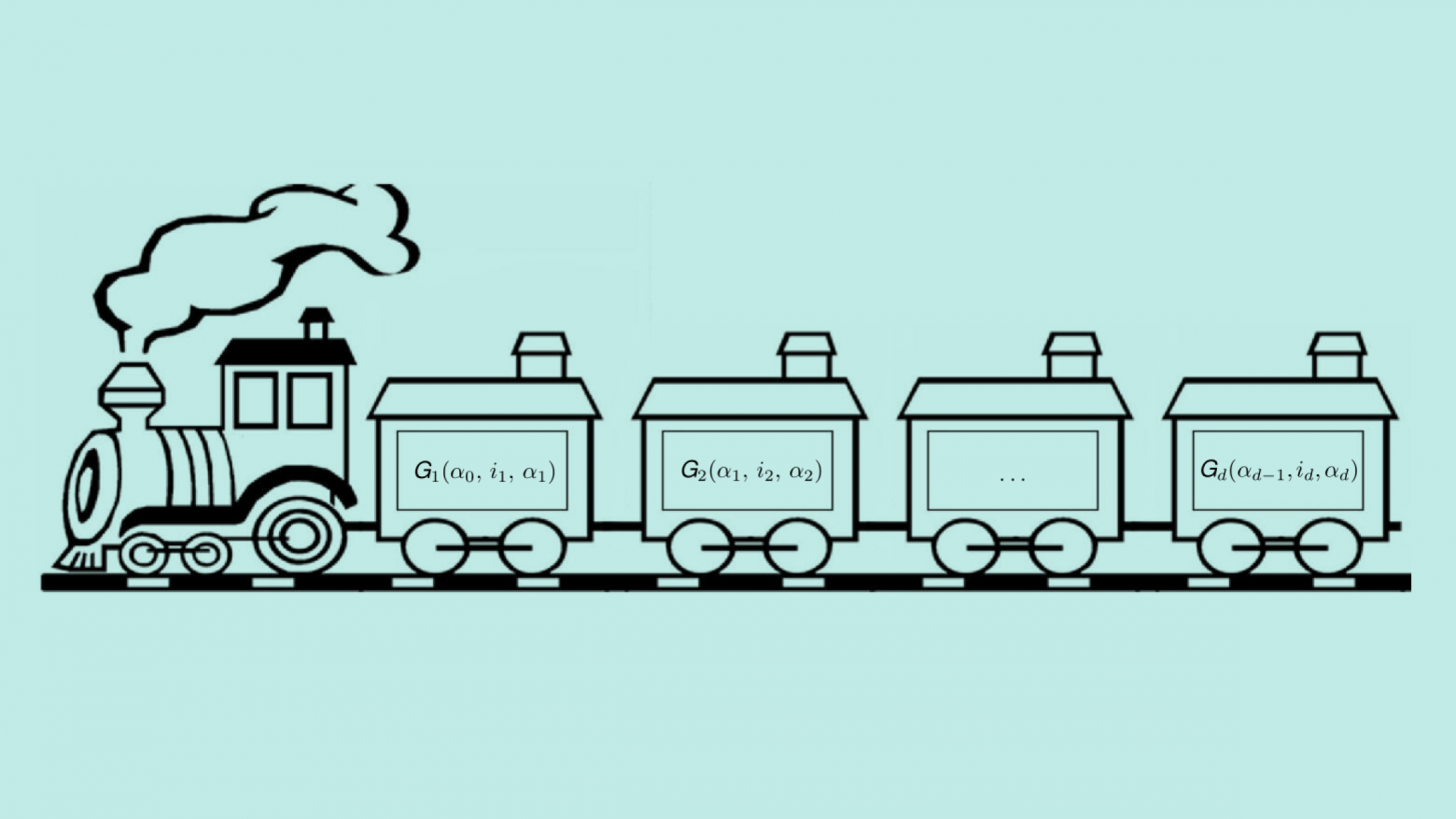
Привет! Меня зовут Глеб Рыжаков, я научный сотрудник Сколтеха. Я занимаюсь математикой, а точнее, линейной алгеброй, и её приложениями к практическим задачам. Сегодня я расскажу вам о нашем исследовании, которое может помочь справиться с проблемой проклятия размерности, которая возникает во множестве статистических задач, включая машинное обучение.

Понятие «проклятие размерности» появилось в середине прошлого века в пионерской работе Ричарда Беллмана, посвященной методам решения сложных задач путём разбиения их на более простые подзадачи. Сегодня оно понимается в более общем смысле, а именно как экспоненциальный — O(n^d) — рост количества необходимых данных и, как следствие, количества памяти, необходимой для их хранения, с ростом размерности пространства d. Когда задачу можно свести к работе с многомерными массивами в общем случае комплексных чисел, удобно говорить о d-мерных тензорах и использовать достижения мультилинейной алгебры. Хорошая новость заключается в том, что там существует такая процедура, как тензорное разложение, которое в ряде случаев может помочь преодолеть проклятие размерности.

Ссылка на первую часть.

Мастер‑теорема

На примере из прошлой части, попробуем сформулировать и обобщить принцип «Разделяй и властвуй». Мы беремся за проблему, размера n, делим эту проблему на подзадачи размером n/b. Количество таких подзадач обозначим числом a. И еще имеется задача скомпоновать результаты выполнения этих a задач размером n/b в итоговый результат для задачи размера n, который будем считать задачей полиномиальной сложности степени c, O(n^c) . Если задача компоновки будет не полиномиальной, то все изложение резко усложнится. Поэтому, давайте позволим задаче компоновки быть полиномиальной, тем более в это попадает очень большое количество алгоритмов.

Привет Хабр! В этой статье поработаем с аудиофайлами, используя библиотеку librosa и алгоритмы Machine learning.

Сначала немного поговорим о том, что такое аудиосигнал. Аудиосигнал представляет собой сложный сигнал, состоящий из нескольких одночастотных звуковых волн, которые распространяются вместе как изменение давления в среде. Каждый аудиосигнал имеет свои определенные характеристики, например, такие как частота, амплитуда, ширина полосы, децибел и т.д. Число волн, производимых сигналом за одну секунду называется частотой. Амплитуда показывает интенсивность звука, то есть является высотой волны. 

Многие оптимизации в компиляторе выглядят естественными. Но IndVarSimplification, предмет этой статьи, сильно выделяется среди них. Это та оптимизация, которая сначала кажется темной магией, но за маской на самом деле скрывается математика.

В этой статье я постарался разобраться, как работает IndVarSimplification. Будет немного кода на Rust, чтение ассемблера и копание в коде LLVM.

• ноутбук,
• DVB-Т-приёмник в виде USB-брелока,
• свободный флеш-накопитель для записи дистрибутива Linux на него.

(сгенерированое изображение)

Существует множество способов создать искусственную нейронную сеть или даже "искусственный интеллект". Но все эти способы обескураживают, от части сложностью которую я не до конца понимаю, отчасти от того, что все сводится к математическим формулам.

В таких подходах нет нечего плохого, они помогают решать поставленные перед ними задачи. Но похоже мне очень хочется написать велосипед.

Часть 1/3

Часть 3/3

Статья «When FTM Discovered MUSIC: Accurate WiFi-based Ranging in the Presence of Multipath» опубликована в материалах Международной конференции IEEE по компьютерным коммуникациям, которая прошла в Торонто, Канада, с 6 по 9 июля 2020 г. (IEEE International Conference on Computer Communications, INFOCOM 2020). Идеи, изложенные в этой публикации, получили дальнейшее развитие, в частности, в статье «FSI: A FTM Calibration Method Using Wi-Fi Physical Layer Information» («FSI: метод калибровки FTM с использованием информации о физическом уровне Wi-Fi»), опубликованной во 2-й части материалов 17-й Международной конференции по беспроводным алгоритмам, системам и приложениям, которая прошла в Даляне, Китай, с 24 по 26 ноября 2022 г. (Wireless Algorithms, Systems, and Applications; WASA 2022).

Вы, наверняка, знаете отчего "гнётся и рвётся" пропеллер на цифровых фото и видео. А какую именно форму принимают лопасти винта? Как зависит их видимая форма от скорости вращения? И причём здесь гиперболы?

Приглашаю любопытных любителей самолётов на небольшое занятие математического кружка.

Приветствую! Я, Ложкинс Алексей, консультант и разработчик оптимизационных решений и математических моделей для бизнеса. Это первая в цикле работ обучающая статья, часть личного образовательного проекта "Make optimization simple". Цель проекта – продемонстрировать доступность технологий и показать на примерах, что моделировать можно без глубокого математического фундамента.

Из статьи вы узнаете об основных компонентах математической оптимизационной задачи на примере классической задачи о назначениях, в частности, распределение машин такси на заказы. Далее, я покажу, как реализовать программный прототип математической модели посредством Python и библиотеки PuLP, а также продемонстрирую, как получить оптимальное решение задачи всего в одной строке кода без реализации специальных алгоритмов.

В этой статье я расскажу об одном способе вычисления x mod p, для p вида (2 ** n - omega), причём omega значительно меньше 2 ** n. Напишу генератор констант на Python. Приведу пару игрушечных примеров на С++, для которых может быть выполнено исчерпывающее тестирование для всех возможных аргументов. А в качестве серьёзной проверки - вычислю 97! mod (2 ** 256 - 2 ** 32 - 977).

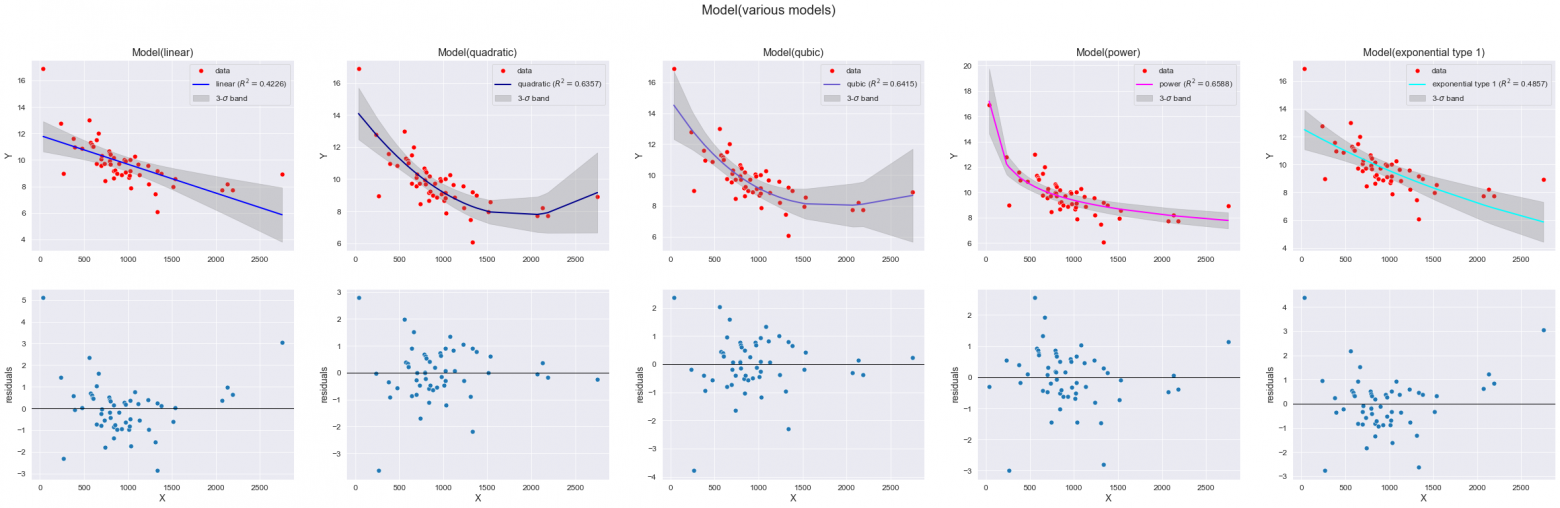
В предыдущих обзорах (https://habr.com/ru/articles/690414/, https://habr.com/ru/articles/695556/) мы рассматривали линейную регрессию. Пришло время переходить к нелинейным моделями. Однако, прежде чем рассматривать полноценный нелинейный регрессионный анализ, остановимся на аппроксимации зависимостей.

Про аппроксимацию написано так много, что, кажется, и добавить уже нечего. Однако, кое-что добавить попытаемся.

При выполнении анализа данных может возникнуть потребность оперативно построить аналитическую зависимость. Подчеркиваю - речь не идет о полноценном регрессионном анализе со всеми его этапами, проверкой гипотез и т.д., а только лишь о подборе уравнения и оценке ошибки аппроксимации. Например, мы хотим оценить характер зависимости между какими-либо показателями в датасете и принять решение о целесообразности более глубокого исследования. Подобный инструмент предоставляет нам тот же Excel - все мы помним, как добавить линию тренда на точечном графике: