Краткий синопсис
По образованию я физик-теоретик, однако имею неплохую математическую базу. В магистратуре одним из предметов была философия, необходимо было выбрать тему и сдать по ней работу. Поскольку большинство вариантов не единожды было обмусолено, то решил выбрать что-то более экзотическое. На новизну не претендую, просто получилось аккумулировать всю/почти всю доступную литературу по этой теме. Философы и математики могут кидаться в меня камнями, буду лишь благодарен за конструктивную критику.
P.S. Весьма «сухой язык», но вполне читабельно после университетской программы. По большей части определения парадоксов брались из Википедии (упрощённая формулировка и готовая TeX-разметка).
Введение
Как сама теория множеств, так и парадоксы, ей присущие, появились не так уж и давно, чуть более ста лет назад. Однако за этот период был пройден большой путь, теория множеств так или иначе фактически стала основой большинства разделов математики. Парадоксы же её, связанные с бесконечностью Кантора, были успешно объяснены буквально за половину столетия.
Следует начать с определения.
Что есть множество? Вопрос достаточно простой, ответ на него вполне интуитивен. Множество это некий набор элементов, представляемый единым объектом. Кантор в своей работе Beiträge zur Begründung der transfiniten Mengenlehre даёт определение: под «множеством» мы понимаем соединение в некое целое M определённых хорошо различимых предметов m нашего созерцания или нашего мышления (которые будут называться «элементами» множества M)[1]. Как видим, суть не изменилась, разница лишь в той части, которая зависит от мировоззрения определяющего. История же теории множеств как в логике так и в математике весьма противоречива. Фактически начало ей положил Кантор в XIX веке, далее Рассел и остальные продолжили работу.
Парадоксы (логики и теории множеств) — (греч.
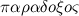
— неожиданный) — формально-логические противоречия, которые возникают в содержательной множеств теории и формальной логике при сохранении логической правильности рассуждения. Парадоксы возникают тогда, когда два взаимоисключающих (противоречащих) суждения оказываются в равной мере доказуемыми. Парадоксы могут появиться как в пределах научной теории, так и в обычных рассуждениях (например, приводимая Расселом перифраза его парадокса о множестве всех нормальных множеств: «Деревенский парикмахер бреет всех тех и только тех жителей своей деревни, которые не бреются сами. Должен ли он брить самого себя?»). Поскольку формально-логическое противоречие разрушает рассуждение как средство обнаружения и доказательства истины (в теории, в которой появляется парадокс, доказуемо любое, как истинное, так и ложное, предложение), возникает задача выявления источников подобных противоречий и нахождения способов их устранения. Проблема философского осмысления конкретных решений парадоксов — одна из важных методологических проблем формальной логики и логических оснований математики.
Целью данной работы является изучение парадоксов теории множеств как наследников античных антиномий и вполне логичных следствий перехода к новому уровню абстракции — бесконечности. Задача — рассмотреть основные парадоксы, их философскую интерпретацию.











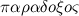 — неожиданный) — формально-логические противоречия, которые возникают в содержательной множеств теории и формальной логике при сохранении логической правильности рассуждения. Парадоксы возникают тогда, когда два взаимоисключающих (противоречащих) суждения оказываются в равной мере доказуемыми. Парадоксы могут появиться как в пределах научной теории, так и в обычных рассуждениях (например, приводимая Расселом перифраза его парадокса о множестве всех нормальных множеств: «Деревенский парикмахер бреет всех тех и только тех жителей своей деревни, которые не бреются сами. Должен ли он брить самого себя?»). Поскольку формально-логическое противоречие разрушает рассуждение как средство обнаружения и доказательства истины (в теории, в которой появляется парадокс, доказуемо любое, как истинное, так и ложное, предложение), возникает задача выявления источников подобных противоречий и нахождения способов их устранения. Проблема философского осмысления конкретных решений парадоксов — одна из важных методологических проблем формальной логики и логических оснований математики.
— неожиданный) — формально-логические противоречия, которые возникают в содержательной множеств теории и формальной логике при сохранении логической правильности рассуждения. Парадоксы возникают тогда, когда два взаимоисключающих (противоречащих) суждения оказываются в равной мере доказуемыми. Парадоксы могут появиться как в пределах научной теории, так и в обычных рассуждениях (например, приводимая Расселом перифраза его парадокса о множестве всех нормальных множеств: «Деревенский парикмахер бреет всех тех и только тех жителей своей деревни, которые не бреются сами. Должен ли он брить самого себя?»). Поскольку формально-логическое противоречие разрушает рассуждение как средство обнаружения и доказательства истины (в теории, в которой появляется парадокс, доказуемо любое, как истинное, так и ложное, предложение), возникает задача выявления источников подобных противоречий и нахождения способов их устранения. Проблема философского осмысления конкретных решений парадоксов — одна из важных методологических проблем формальной логики и логических оснований математики.
 Но нам был интересен обратный вопрос, как, имея, например, изображение сердечка, получить выражение для функции, графиком которой будет это самое сердечко.
Но нам был интересен обратный вопрос, как, имея, например, изображение сердечка, получить выражение для функции, графиком которой будет это самое сердечко.