
Фрактальное пламя (или фрактальные искры, англ. fractal flame) – алгоритм, предложенный Скоттом Дрейвсом (Scott Draves) и использующий для построения изображений системы итерируемых функций (СИФ). Благодаря разным значениям seed для генератора псевдослучайных чисел можно получить множество разнообразных «картин». Хотя фрактальность в них просматривается далеко не всегда, результаты получаются очень интересными.
Под катом – краткое описание основных моментов реализации алгоритма.
Для начала, как и в обычных СИФ, нам понадобится узнать коэффициенты для каждого аффинного преобразования плоскости (их может быть несколько; каждое следующее будет вносить свои «мазки» на картину, а также изменять вклад предыдущих). В матричной форме это преобразование выглядит следующим образом:
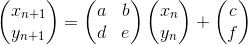
Необходимо подобрать такие коэффициенты, чтобы полученное преобразование было сжимающим, то есть таким, что его коэффициент масштабирования меньше единицы. Этих преобразований должно быть несколько, и если выбирать случайным образом одно из них, чтобы вычислить новые координаты точки и отобразить ее на экране, мы получим аттрактор — множество точек, из которых и будет состоять изображение.
Используя датчик псевдослучайных чисел, получить такие коэффициенты несложно. При этом надо проверить 3 условия:
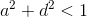
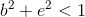
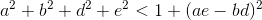
Все это относится к коэффициентам, задающим линейное преобразование. Оставшиеся два,
 и
и 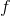 , выполняют трансляцию – перемещение точки на некоторое расстояние. Желательно, чтобы
, выполняют трансляцию – перемещение точки на некоторое расстояние. Желательно, чтобы  ,
, 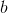 ,
, 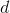 и
и  находились на отрезке
находились на отрезке 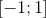 или
или 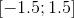 . Для
. Для  и
и 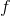 это необязательно, однако не стоит задавать слишком большой отрезок, иначе изображение получится разреженным.
это необязательно, однако не стоит задавать слишком большой отрезок, иначе изображение получится разреженным.Кроме того, вместе с каждым набором коэффициентов, нужно сохранить стартовые значения трех цветовых составляющих модели RGB, которые будут присваиваться пикселю, в который попали первый раз. Это также делается с помощью датчика случайных чисел и особых трудностей не представляет.
Теперь необходимо определиться, изображение какого разрешения хотим получить и подготовить массив пикселей, каждый элемент которого будет хранить:
- координаты x и y;
- значения R, G и B;
- число попаданий.
Далее приведены некоторые нелинейные преобразования, которые будут выполняться над значениями x и y, полученными после выполнения одного из аффинных преобразований:
- Синусоидальное:
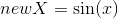 ,
, 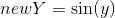 ;
; - Сферическое:
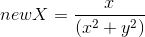 ,
, 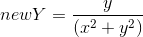 ;
; - Полярное:
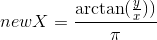 ,
, 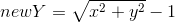 ;
; - Сердце:
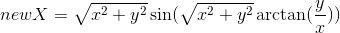 ,
, 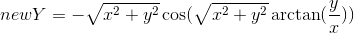 ;
; - Диск:
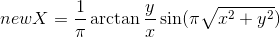 ,
, 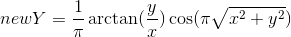 ;
;
В конце статьи – примеры изображений, полученных с использованием этих и некоторых других преобразований, а далее – псевдокод процедуры рендеринга:
void render(int n, int eqCount, int it, int xRes, int yRes)
{
Генерируем eqCount аффинных преобразований со стартовыми цветами;
for(int num=0; num<n; num++)
{
//Для изображения размером 1920х1080 можно
//взять XMIN=-1.777,XMAX=1.777,YMIN=-1,YMAX=1
//В этом случае в большинстве нелинейных преобразований с боков не будет оставаться черных областей
newX=Rand(XMIN,XMAX);
newY=Rand(YMIN,YMAX);
//Первые 20 итераций точку не рисуем, т.к. сначала надо найти начальную
for(int step=-20; step<it; step++)
{
//Выбираем одно из аффинных преобразований
i=Rand(0,eqCount);
//и применяем его
x=coeff[i].a*newX+coeff[i].b*newY+coeff[i].c;
y=coeff[i].d*newX+coeff[i].e*newY+coeff[i].f;
Применяем нелинейное преобразование;
if(step>=0 && newX∈[XMIN,XMAX] && newY∈[YMIN,YMAX])
{
//Вычисляем координаты точки, а затем задаем цвет
x1=xRes-Trunc(((XMAX-newX)/(XMAX-XMIN))*xRes);
y1=yRes-Trunc(((YMAX-newY)/(YMAX-YMIN))*yRes);
//Если точка попала в область изображения
if(x1<xRes && y1<yRes)
{
//то проверяем, первый ли раз попали в нее
if(pixels[x1][y1].counter==0)
{
//Попали в первый раз, берем стартовый цвет у соответствующего аффинного преобразования
pixels[x1][y1].red=coeff[i].red;
pixels[x1][y1].green=coeff[i].green;
pixels[x1][y1].blue=coeffs[i].blue;
} else
{
//Попали не в первый раз, считаем так:
pixels[x1][y1].red=(pixels[x1][y1].red+coeff[i].red)/2;
pixels[x1][y1].green=(pixels[x1][y1].green+coeff[i].green)/2;
pixels[x1][y1].blue=(pixels[x1][y1].blue+coeff[i].blue)/2;
}
//Увеличиваем счетчик точки на единицу
pixels[x1][y1].counter++;
}
}
}
}
}
Итак, теперь уже можно вывести наше изображение, однако результат в этом случае получится слишком зашумленным, так как яркость всех пикселей одинакова. Чтобы это исправить, надо провести логарифмическую и гамма-коррекцию, отразив число попаданий в каждую точку с помощью яркости. Ниже приведен код, выполняющий коррекцию:
void correction(int xRes, int yRes)
{
max=0.0;
gamma=2.2;
for (int row=0; row<xRes; row++)
for (int col=0; col<yRes; col++)
if (pixels[row][col].counter != 0)
{
pixels[row][col].normal=log10(pixels[row][col].counter);
if (pixels[row][col].normal>max)
max = pixels[row][col].normal;
}
for (int row=0; row<xRes; row++)
for (int col=0; col<yRes; col++)
{
pixels[row][col].normal/=max;
pixels[row][col].red =pixels[row][col].red*pow(pixels[row][col].normal,(1.0 / gamma));
pixels[row][col].green =pixels[row][col].green*pow(pixels[row][col].normal,(1.0 / gamma));
pixels[row][col].blue =pixels[row][col].blue*pow(pixels[row][col].normal,(1.0 / gamma));
}
}
Разница между изображением без коррекции (выше) и с коррекцией (ниже)



Ну а теперь обещанные изображения с различными нелинейными преобразованиями
Синусоидальное

Сферическое

Полярное

Сердце

Диск

«Ракушка»

Гиперболическое

Водоворот

Волны


Сферическое

Полярное

Сердце

Диск

«Ракушка»

Гиперболическое

Водоворот

Волны

А что если применять не одно и то же нелинейное преобразование, а случайным образом выбирать из нескольких?









Исходный код
Реализация алгоритма от Джеймса Маккарти на языке Си находится здесь, а статья Скотта Дрейвса на основе которой и создавался алгоритм — здесь.












