
Перевод поста Devendra Kapadia "New in the Wolfram Language: Symbolic PDEs".
Код, приведенный в статье, можно скачать здесь.
Выражаю огромную благодарность Кириллу Гузенко KirillGuzenko за помощь в переводе и подготовке публикации.
Уравнения в частных производных (УрЧП) играют очень важную роль в математике и ее приложениях. Их можно использовать для моделирования реальных явлений, таких как колебания натянутой струны, распространения потока тепла в стержне, в финансовых областях. Цель этой статьи — приоткрыть завесу в мир УрЧП (тем кто еще с ним не знаком) и ознакомить читателя с тем, как можно эффективно решать УрЧП в Wolfram Language, используя новый функционал для решения краевых задач в DSolve, а так же новую функцию DEigensystem, которая появилась в версии 10.3.
История УрЧП восходит к работам известных математиков восемнадцатого века — Эйлера, Даламбера, Лапласа, однако развитие этой области в последние три столетия так и не остановилось. И потому в статье я приведу как классические, так и современные примеры УрЧП, что позволит рассмотреть эту область знаний под разными углами.
Давайте начнем с рассмотрения колебаний натянутой струны с длиной π, закрепленной на обоих концах. Колебания струны можно смоделировать с помощью одномерного волнового уравнения, приведённого ниже. Здесь u(x,t) — вертикальное смещение точки струны с координатой х в момент времени t:
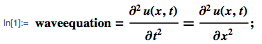
Затем мы задаём граничные условия, указав тем самым, что концы струны при колебаниях сохраняют свои положения.
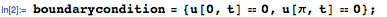
Зададим теперь начальные условия для движения струны, указав смещения и скорости различных точек струны в момент времени t=0:
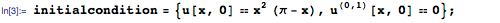
Теперь мы можем использовать DSolve для решения волнового уравнения с начальными и краевыми условиями:
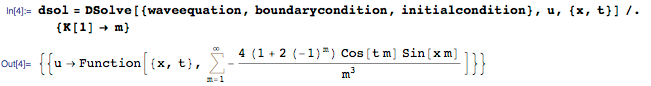
Как указано выше, решение есть бесконечная сумма тригонометрических функций. Сумма возвращается в невычисленной форме (Inactive), поскольку каждый отдельный член разложения имеет физическую интерпретацию, и зачастую даже небольшое количество членов может являться хорошим приближением. К примеру, мы можем взять первые четыре члена для получения приближенного решения asol(x,t)
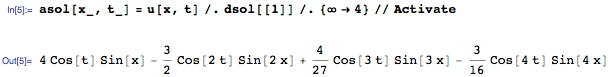
Каждый член в сумме представляет собой стоячую волну, которые могут быть представлены следующим образом:
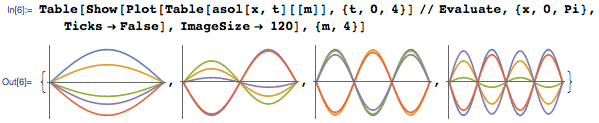
И все эти стоячие волны складываются воедино, образуя гладкую кривую, как показано на анимации ниже:
Волновое уравнение относится к классу линейных гиперболических уравнений в частных производных, описывающих распространение сигналов с конечными скоростями. Это УрЧП представляет собой удобный способ для моделирования колебаний в струне или в каком-то другом деформирумом теле, однако ещё более важную роль оно играет в современной физике и инженерных приложениях, т.к. оно описывает распространение света и электромагнитных волн.
Давайте теперь смоделируем поток тепла в стержне единичной длины, изолированном с обоих концов, с помощью представленного ниже уравнения теплопроводности:
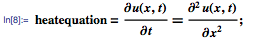
Поскольку стержень изолирован с обоих концов, то через них проходит нулевой поток тепла, что можно выразить как граничные условия вида х = 0 и х = 1:
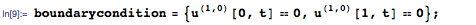
Теперь нужно указать начальное температурное распределение в стержне. В этом примере мы будем использовать приведённую ниже линейную функцию. В левом конце (х = 0) начальная температура — 20 градусов, в правом (х = 1) — 100:
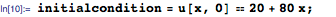
И теперь мы можем решить уравнение теплопроводности с заданными условиями:

Как и в приведённом выше примере с волновым уравнением, мы можем извлечь несколько членов суммы и получить приближенное решение:
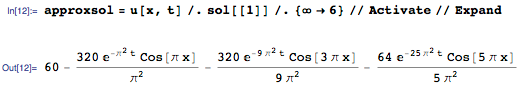
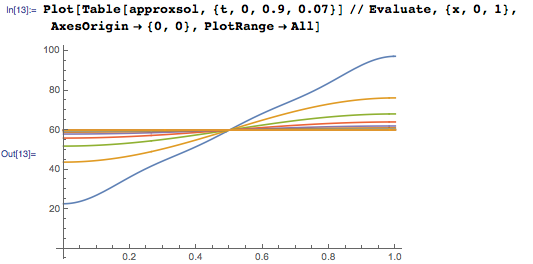
Первый член приближенного решения — 60 — среднее от температур на границах стержня, и она является стационарной температурой для этого стержня. Как показано на графике функции температуры от длины, представленном ниже, температура стержня быстро достигает стационарного значения в 60 градусов:
Уравнение теплопроводности относится к классу линейных параболических уравнений в частных производных, которые описывают процессы диффузии. Это простое на вид уравнение часто можно встретить в самых различных, а иногда и весьма неожиданных областях. Далее в статье мы рассмотрим два примера этого явления.
Рассмотрим теперь уравнение Лапласа, которое используется для моделирования стационарного состояния систем, т. е. поведения после некоторых зависящих от времени уже законченных переходных процессов. В двумерном случае это уравнение можно представить следующим образом:
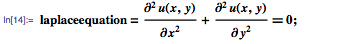
Ограничим координаты х и у прямоугольной областью Ω, как показано ниже:
Классическая задача Дирихле — найти функцию u(x,y), удовлетворяющую уравнению Лапласа внутри области Ω с заданным условием Дирихле (DirichletCondition), которое определяет значения на границах области Ω, как показано ниже:

Задачу Дирихле можно решить с помощью функции DSolve, весьма изящно задав при этом область:

Как и в примерах ранее, мы можем извлечь некоторое количество членов (скажем, 100) из суммы и визуализировать решение:
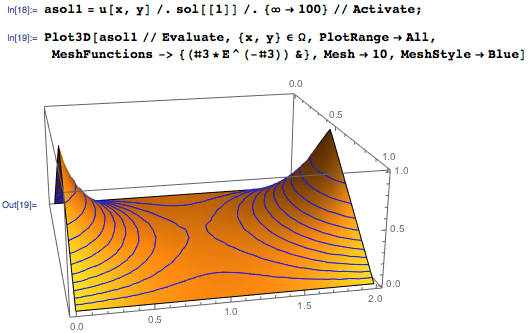
Следует заметить, что решение u(x,y) задачи Дирихле представляется гладким в Ω, несмотря на то, что граничные условия имеют резкие черты. Помимо этого, u(x,y) достигает экстремальных значений на границах, в то время как в центре прямоугольника находится седловая точка. Эти черты характерны для линейных эллиптических уравнений — класса уравнений в частных производных, к которым и принадлежит уравнение Лапласа.
Волновое уравнение, уравнение теплопроводности, уравнение Лапласа — самые известные примеры классических УрЧП. Теперь мы рассмотрим три примера типичных современных УрЧП, первым среди которых будет уравнение Бюргерса для вязкой жидкости, которое может быть представлено следующим образом:
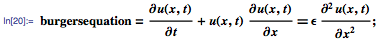
Это нелинейное УрЧП было введено Иоханнесом Бюргерсом в сороковых годах в качестве простой модели для турбулентных потоков (параметр ϵ в уравнении представляет собой вязкость жидкости). Однако, десять лет спустя, Э. Хопф и Д. Коул показали, что уравнение Бюргерса сводится к уравнению теплопроводности, а это значит, что данное уравнение не может проявлять хаотического поведения. Преобразование Коула-Хопфа позволяет решать уравнения Бюргерса в замкнутой форме для начального условия, заданного, к примеру, так:
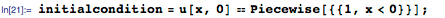
В этом примере мы будем использовать функцию DSolveValue, которая возвращает только выражение для решения. Члены с функцией ошибок (Erf) в формуле ниже возникают из решения соответствующей граничной задачи теплового уравнения:

Представленный ниже график демонстрирует изменение во времени гипотетического одномерного поля скоростей потока. Решение представляется гладким для положительного ϵ, при том что начальное условие есть кусочно заданная функция:
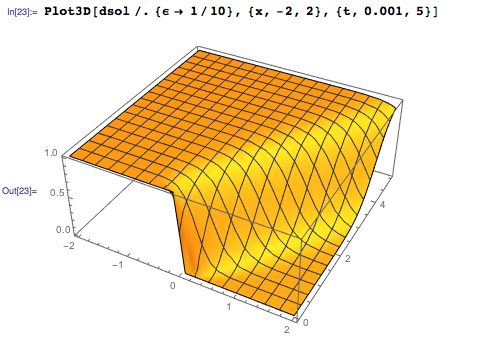
Как можно заметить на нижепреведённых графиках, решение стремится к разрывному при сремлении вязкости ϵ к нулю. Подобные решения с резким переходом (shock solutions) — известная особенность уравнений Бюргерса для невязкой (ϵ = 0) среды.

В качестве второго примера современных УрЧП рассмотрим уравнение Блэка-Шоулза, используемое в финансовых расчётах. Это уравнение впервые представили Фишер Блэк и Майрон Шоулз в 1973 году в качестве модели для определения теоретической цены на европейские опционы, и формулируется оно следующим образом:
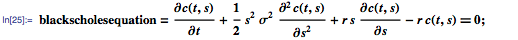
где:
c — цена опциона как функция от стоимости акций s и времени t,
r — процентная ставка без риска,
σ — волатильность акций.
В их эпохальной статье (которая была процитирована более 28000 раз), Блэк и Шоулз отметили, что их уравнения с помощью преобразования переменных могут быть сведены к уравнению теплопроводности. Это резкое упрощение приводит к знаменитой формуле Блэка-Шоулза для европейских опционов с конечными условиями, основанными на цене исполнения (strike price) k актива в момент времени t=Т:

Вооружившись этой формулой, мы можем вычислить значения финансовых опционов для типичных значений параметров:
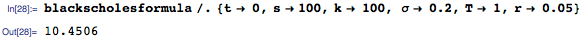
Ответ согласуется со значением, полученным с помощью встроенной функции FinancialDerivative:

В качестве третьего примера современных УрЧП рассмотрим уравнение Шредингера для электрона в одномерной потенциальной яме с глубиной d и соответствующим начальным условием. Уравнение и условия можно сформулировать следующим образом:
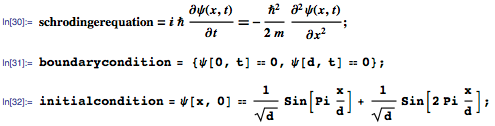
Этот пример имеет элементарное решение, которое принимает мнимые значения из-за наличия I в уравнении Шредингера:

Функция плотности вероятности для электрона ρ = Ψ⊹ Ψ, с использованием подходящих значений параметров в задаче, может быть вычислена следующим образом:

Мы можем создать анимацию изменения плотности вероятности во времени, которая показывает, что «центр» электрона в яме движется из стороны в сторону:

Собственные значения и собственные функции играют важную роль как в решении уравнения Шрёдингера, так и в других УрЧП. В частности, они предоставляют «строительные блоки» для решений волновых уравнений и уравнений теплопроводности в виде бесконечных сумм, которые приводились ранее в статье. Поэтому, в качестве нашего последнего примера рассмотрим задачу о нахождении девяти наименьших собственных значений и собственных функций для оператора Лапласа с однородным (нулевым) условием Дирихле для трехмерной сферической области. Найдем девять наименьших значений λ и соответствующих им функций ϕ, удовлетворяющих Λϕ = λ ϕ, которые определяются следующим образом:
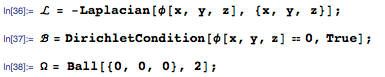
Новая функция DEigensystem в версии 10.3 позволяет вычислить требуемые собственные значения и функции следующим образом:
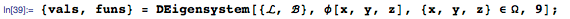
Собственные значения в этой задаче выражаются через BesselJZero. Вот пример:
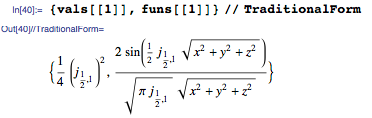
Собственные значения можно визуализировать с помощью функции DensityPlot3D, которая возвращает красивые графики, как показано ниже:

УрЧП являются важным инструментом во многих отраслях науки и техники, в статистике и финансах. На более фундаментальном уровне они предоставляют точные математические формулировки некоторых самых глубоких и тонких вопросов о нашей Вселенной, скажем, о возможности существования голых сингулярностей. По моему опыту, изучение УрЧП награждает редким сочетанием из практических идей и интеллектуального удовлетворения.
Рекомендую изучить документацию по DSolve, NDSolve, DEigensystem, NDEigensystem и методу конечных элементов, чтобы узнать больше о различных подходах к решению УрЧП в Wolfram Language.
УрЧП в символьной форме поддерживаются в Wolfram Mathematica и Wolfram Language с версии 10.3, а в ближайшее время будут представлены и во всех остальных программных продуктах Wolfram.