Комментарии 33
Реквестирую расчеты смартфонов на Windows!
И наконец, обещанный результат: на iPhone 5S миллион знаков числа Пи вычислялись 49296 секунд, или около 14 часов
Фиговенький результат.
Вот, например: http://numbers.computation.free.fr/Constants/PiProgram/pifast.html
This mode is the fastest when there are enough physical memory.
Timings sample on a Pentium 4 1.4 Ghz with 1024 Mo running on Windows
NT (notice that no particular compilation has been made to benefit from
Pentium 4 specific instructions) :
PI Computation : (timings with version 4.1)
1 Million decimal digits : 9.69 seconds
2 Million decimal digits : 22.78 seconds
4 Million decimal digits : 50.80 seconds
8 Million decimal digits : 116.38 seconds
16 Million decimal digits : 264.9 seconds
32 Million decimal digits : 583.25 seconds
64 Million decimal digits : 1327 seconds
128 Million decimal digits : 2974 secondsНа моем ноуте 10 млн. цифр — 23 сек
Спасибо, интересно.
Но во-первых, вышеприведенный алгоритм был закодирован за полчаса, и вряд ли претендует на «the fastest windows program to compute pi» (у них там уже 4.3 версия).
Во-вторых, the source code of PiFast is not available — проверить на iPhone все равно не получится.
Но во-первых, вышеприведенный алгоритм был закодирован за полчаса, и вряд ли претендует на «the fastest windows program to compute pi» (у них там уже 4.3 версия).
Во-вторых, the source code of PiFast is not available — проверить на iPhone все равно не получится.
Может, тогда ради интереса попробуйте оптимизировать?
Скачал первую попавшеюся программку для расчета Пи на свой андроид, девайс старый, ему почти 4 года, Snapdragon 410 — миллион знаков посчитал за 13.34 секунды. А ведь iphone SE в разы шустрее моего кирпича.
Скачал первую попавшеюся программку для расчета Пи на свой андроид, девайс старый, ему почти 4 года, Snapdragon 410 — миллион знаков посчитал за 13.34 секунды. А ведь iphone SE в разы шустрее моего кирпича.
Да, допускаю что я что-то пропустил :) Попробую конечно, результат в статье дополню по появлении новых результатов.
Кстати, перепроверил код еще раз. Можно вынести вычисление 26680*640320*640320 за цикл, можно заменить 3 умножения на одну функцию степени. По прикидке, это даст выигрыш в 5% где-то. Можно запустить в 2 потока — получится допустим, не 13 часов а 6.
Но так чтобы 13 секунд на старом смартфоне — странно. Тут по ссылке выше писали что 10секунд на Pentium-4 считалось, который явно помощнее будет. Может у них просто заранее подсчитанный файл в памяти лежит? :)
Ну либо я не учитываю что-то, хз.
Но так чтобы 13 секунд на старом смартфоне — странно. Тут по ссылке выше писали что 10секунд на Pentium-4 считалось, который явно помощнее будет. Может у них просто заранее подсчитанный файл в памяти лежит? :)
Ну либо я не учитываю что-то, хз.
>10секунд на Pentium-4 считалось, который явно помощнее будет.
Твои данные сильно устарели :)
http://browser.primatelabs.com/v4/cpu/264152
http://browser.primatelabs.com/ios-benchmarks
Разница в 4 раза насколько я понимаю, и не в пользу 4 пня )
Твои данные сильно устарели :)
http://browser.primatelabs.com/v4/cpu/264152
http://browser.primatelabs.com/ios-benchmarks
Разница в 4 раза насколько я понимаю, и не в пользу 4 пня )
В общем нашел, там действительно используется другой алгоритм. Поправил результаты в тексте.
Что интересно, после генерации все число посмотреть невозможно, прога показывает только последние цифры.
А если захотеть посмотреть N-е число предупреждает что это будет очень долго.
Возможно какая-то хитрость там и есть.
Вот ссылка на гугл маркет link
Cкрин после расчетов под спойлером
И на этот раз даже еще быстрее посчитало :)
А если захотеть посмотреть N-е число предупреждает что это будет очень долго.
Возможно какая-то хитрость там и есть.
Вот ссылка на гугл маркет link
Cкрин после расчетов под спойлером
Скрытый текст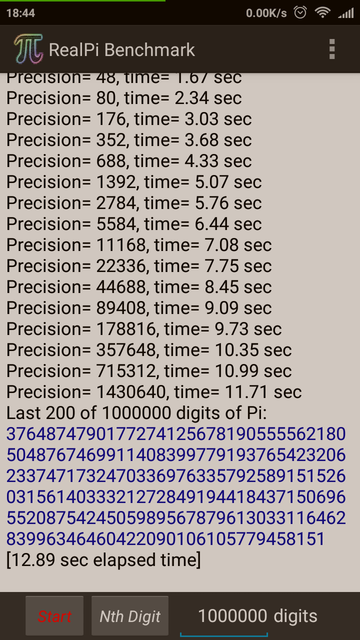

И на этот раз даже еще быстрее посчитало :)
the fastest windows program to compute pi
Ну, это на 2003 год.
Там используется одно важное алгоритмическое решение: http://numbers.computation.free.fr/Constants/Algorithms/splitting.html
Кстати вопрос. А где именно в Ведах есть значение числа Пи ну и вся прочая математика известная древним индийцам? Хотелось бы почитать оригинал переведенный на русский либо английский. Нагуглить ничего не получилось — вся поисковая выдача завалена философией адвайты и чем угодно но только не математикой.
Не смог удержаться, посчитал все варианты рационального приближения в разумных пределах по поиску числа Pi делением двух простых чисел, как делали в древнем мире, по моему интересная задача:
ошибка; действие
4,7%; 9/3
3,34%; 13/4
1,8%; 16/5
0,8%; 19/6
0,04%; 22/7 — удобный вариант для столь малых чисел (даже лучше чем Чжан Хэн во II веке предложил 92/29 с ошибкой в 1%), первым предложил Архимед.
0,039%; 179/57
0,03%; 201/64
0,024%; 223/71
0,018%; 245/78
0,013%; 267/85
0,009%; 289/92
0,0056%; 311/99
0,0026%; 333/106 — почти как в том религиозном ведийском тексте, но точнее почти в 40 раз, там 0,086% ошибка, казалось бы очень близко, но немного не попали.
8,49136715180762E-6%; 355/113 — тоже удобный вариант, при больших последующих цифрах точность не растет существенно. В 480-х годах китайский математик Цзу Чунчжи продемонстрировал… Это значение оставалось самым точным приближением числа pi в течение последующих 900 лет.
И не удивительно, следующая итерация на порядок сложнее. Резкий рост сложности при небольшом росте точности:
8,47383188246871E-6%; 52163/16604
8,35915415110094E-6%; 52518/16717
3,6375309526024E-11%; 3126535/995207
…
ошибка; действие
4,7%; 9/3
3,34%; 13/4
1,8%; 16/5
0,8%; 19/6
0,04%; 22/7 — удобный вариант для столь малых чисел (даже лучше чем Чжан Хэн во II веке предложил 92/29 с ошибкой в 1%), первым предложил Архимед.
0,039%; 179/57
0,03%; 201/64
0,024%; 223/71
0,018%; 245/78
0,013%; 267/85
0,009%; 289/92
0,0056%; 311/99
0,0026%; 333/106 — почти как в том религиозном ведийском тексте, но точнее почти в 40 раз, там 0,086% ошибка, казалось бы очень близко, но немного не попали.
8,49136715180762E-6%; 355/113 — тоже удобный вариант, при больших последующих цифрах точность не растет существенно. В 480-х годах китайский математик Цзу Чунчжи продемонстрировал… Это значение оставалось самым точным приближением числа pi в течение последующих 900 лет.
И не удивительно, следующая итерация на порядок сложнее. Резкий рост сложности при небольшом росте точности:
8,47383188246871E-6%; 52163/16604
8,35915415110094E-6%; 52518/16717
Тут не интересно почти одинаковые ряды цифр без исторической ценности
8,24601634587631E-6%; 52873/16830
8,13438766487423E-6%; 53228/16943
8,02423812605099E-6%; 53583/17056
7,91553851069651E-6; 53938/17169
7,80826037757015E-6; 54293/17282
7,70237603462907E-6; 54648/17395
7,597858482485E-6; 55003/17508
7,49468142854007E-6; 55358/17621
7,39281925871516E-6; 55713/17734
7,29224698090669E-6; 56068/17847
7,19294026739402E-6; 56423/17960
7,09487535588881E-6; 56778/18073
6,99802912021403E-6; 57133/18186
6,90237897135335E-6; 57488/18299
6,80790289985851E-6; 57843/18412
6,71457940517032E-6; 58198/18525
6,62238752389025E-6; 58553/18638
6,53130680150882E-6; 58908/18751
6,44131727826978E-6; 59263/18864
6,35239944676271E-6; 59618/18977
6,26453429433043E-6; 59973/19090
6,17770321825414E-6; 60328/19203
6,09188808229667E-6; 60683/19316
6,00707116015922E-6; 61038/19429
5,92323512134561E-6; 61393/19542
5,84036305943381E-6; 61748/19655
5,75843844966859E-6; 62103/19768
5,67744513482567E-6; 62458/19881
5,59736731107594E-6; 62813/19994
5,51818954212124E-6; 63168/20107
5,43989675919436E-6; 63523/20220
5,36247419038006E-6; 63878/20333
5,28590741715819E-6; 64233/20446
5,21018231786058E-6; 64588/20559
5,13528511007836E-6; 64943/20672
5,0612022658472E-6; 65298/20785
4,98792058232629E-6; 65653/20898
4,91542713939092E-6; 66008/21011
4,8437092854967E-6; 66363/21124
4,77275463767957E-6; 66718/21237
4,70255108155574E-6; 67073/21350
4,63308674305014E-6; 67428/21463
4,56435003080379E-6; 67783/21576
4,49632955135901E-6; 68138/21689
4,4290141657026E-6; 68493/21802
4,36239297513005E-6; 68848/21915
4,29645530710975E-6; 69203/22028
4,23119067287555E-6; 69558/22141
4,16658883810578E-6; 69913/22254
4,10263975224427E-6; 70268/22367
4,03933357677188E-6; 70623/22480
3,976660656935E-6; 70978/22593
3,91461153588123E-6; 71333/22706
3,85317695465947E-6; 71688/22819
3,79234782394828E-6; 72043/22932
3,73211523819166E-6; 72398/23045
3,67247046146331E-6; 72753/23158
3,61340492746656E-6; 73108/23271
3,55491026780599E-6; 73463/23384
3,49697819890105E-6; 73818/23497
3,43960069161564E-6; 74173/23610
3,38276978749271E-6; 74528/23723
3,32647772597646E-6; 74883/23836
3,27071687373333E-6; 75238/23949
3,2154797529236E-6; 75593/24062
3,16075901292983E-6; 75948/24175
3,10654744449258E-6; 76303/24288
3,05283799384627E-6; 76658/24401
2,99962369204018E-6; 77013/24514
2,94689773975319E-6; 77368/24627
2,89465342247904E-6; 77723/24740
2,84288420947691E-6; 78078/24853
2,79158361241342E-6; 78433/24966
2,74074532672059E-6; 78788/25079
2,69036310437372E-6; 79143/25192
2,64043085284191E-6; 79498/25305
2,59094256440911E-6; 79853/25418
2,54189234444568E-6; 80208/25531
2,49327439727263E-6; 80563/25644
2,44508305443319E-6; 80918/25757
2,39731270401382E-6; 81273/25870
2,34995786132321E-6; 81628/25983
2,30301311234906E-6; 81983/26096
2,25647318443711E-6; 82338/26209
2,21033284734052E-6; 82693/26322
2,16458696976308E-6; 83048/26435
2,1192305193592E-6; 83403/26548
2,0742585485981E-6; 83758/26661
2,02966619476384E-6; 84113/26774
1,9854486516837E-6; 84468/26887
1,94160124040716E-6; 84823/27000
1,89811931025535E-6; 85178/27113
1,85499832363578E-6; 85533/27226
1,81223378536343E-6; 85888/27339
1,76982132747545E-6; 86243/27452
1,72775658200904E-6; 86598/27565
1,6860353223594E-6; 86953/27678
1,64465335019335E-6; 87308/27791
1,60360652372093E-6; 87663/27904
1,5628908142386E-6; 88018/28017
1,52250222131442E-6; 88373/28130
1,48243680105968E-6; 88728/28243
1,44269072267208E-6; 89083/28356
1,40326015534932E-6; 89438/28469
1,36414138137554E-6; 89793/28582
1,32533069717068E-6; 90148/28695
1,28682448396948E-6; 90503/28808
1,24861917954991E-6; 90858/28921
1,21071124996156E-6; 91213/29034
1,1730972602046E-6; 91568/29147
1,13577380355084E-6; 91923/29260
1,09873750154369E-6; 92278/29373
1,06198508881297E-6; 92633/29486
1,02551328585272E-6; 92988/29599
9,89318897971778E-7; 93343/29712
9,53398772886396E-7; 93698/29825
9,17749814856038E-7; 94053/29938
8,82368942275979E-7; 94408/30051
8,47253172492096E-7; 94763/30164
8,12399508714484E-7; 95118/30277
7,77805053103839E-7; 95473/30390
7,4346690782087E-7; 95828/30503
7,09382231569494E-7; 96183/30616
6,75548239596832E-7; 96538/30729
6,4196216128582E-7; 96893/30842
6,08621310834192E-7; 97248/30955
5,75522988303898E-7; 97603/31068
5,42664550300092E-7; 97958/31181
5,10043424106933E-7; 98313/31294
4,7765702287279E-7; 98668/31407
4,45502844560836E-7; 99023/31520
4,13578387134253E-7; 99378/31633
3,81881205099427E-7; 99733/31746
3,50408867098552E-7; 100088/31859
3,19158998317026E-7; 100443/31972
2,88129238076054E-7; 100798/32085
2,57317296375846E-7; 101153/32198
2,26720854945019E-7; 101508/32311
1,96337680326993E-7; 101863/32424
1,66165553200993E-7; 102218/32537
1,36202268382054E-7; 102573/32650
1,06445663092611E-7; 102928/32763
7,68936310983031E-8; 103283/32876
4,75440378931792E-8; 103638/32989
1,83948337860874E-8; 103993/33102
1,05560450499157E-8; 104348/33215
3,89472739745897E-9; 208341/66317
9,27657882316268E-10%; 312689/99532
2,77418946985962E-10%; 833719/265381
5,12666416965132E-11%; 1146408/364913
8,13438766487423E-6%; 53228/16943
8,02423812605099E-6%; 53583/17056
7,91553851069651E-6; 53938/17169
7,80826037757015E-6; 54293/17282
7,70237603462907E-6; 54648/17395
7,597858482485E-6; 55003/17508
7,49468142854007E-6; 55358/17621
7,39281925871516E-6; 55713/17734
7,29224698090669E-6; 56068/17847
7,19294026739402E-6; 56423/17960
7,09487535588881E-6; 56778/18073
6,99802912021403E-6; 57133/18186
6,90237897135335E-6; 57488/18299
6,80790289985851E-6; 57843/18412
6,71457940517032E-6; 58198/18525
6,62238752389025E-6; 58553/18638
6,53130680150882E-6; 58908/18751
6,44131727826978E-6; 59263/18864
6,35239944676271E-6; 59618/18977
6,26453429433043E-6; 59973/19090
6,17770321825414E-6; 60328/19203
6,09188808229667E-6; 60683/19316
6,00707116015922E-6; 61038/19429
5,92323512134561E-6; 61393/19542
5,84036305943381E-6; 61748/19655
5,75843844966859E-6; 62103/19768
5,67744513482567E-6; 62458/19881
5,59736731107594E-6; 62813/19994
5,51818954212124E-6; 63168/20107
5,43989675919436E-6; 63523/20220
5,36247419038006E-6; 63878/20333
5,28590741715819E-6; 64233/20446
5,21018231786058E-6; 64588/20559
5,13528511007836E-6; 64943/20672
5,0612022658472E-6; 65298/20785
4,98792058232629E-6; 65653/20898
4,91542713939092E-6; 66008/21011
4,8437092854967E-6; 66363/21124
4,77275463767957E-6; 66718/21237
4,70255108155574E-6; 67073/21350
4,63308674305014E-6; 67428/21463
4,56435003080379E-6; 67783/21576
4,49632955135901E-6; 68138/21689
4,4290141657026E-6; 68493/21802
4,36239297513005E-6; 68848/21915
4,29645530710975E-6; 69203/22028
4,23119067287555E-6; 69558/22141
4,16658883810578E-6; 69913/22254
4,10263975224427E-6; 70268/22367
4,03933357677188E-6; 70623/22480
3,976660656935E-6; 70978/22593
3,91461153588123E-6; 71333/22706
3,85317695465947E-6; 71688/22819
3,79234782394828E-6; 72043/22932
3,73211523819166E-6; 72398/23045
3,67247046146331E-6; 72753/23158
3,61340492746656E-6; 73108/23271
3,55491026780599E-6; 73463/23384
3,49697819890105E-6; 73818/23497
3,43960069161564E-6; 74173/23610
3,38276978749271E-6; 74528/23723
3,32647772597646E-6; 74883/23836
3,27071687373333E-6; 75238/23949
3,2154797529236E-6; 75593/24062
3,16075901292983E-6; 75948/24175
3,10654744449258E-6; 76303/24288
3,05283799384627E-6; 76658/24401
2,99962369204018E-6; 77013/24514
2,94689773975319E-6; 77368/24627
2,89465342247904E-6; 77723/24740
2,84288420947691E-6; 78078/24853
2,79158361241342E-6; 78433/24966
2,74074532672059E-6; 78788/25079
2,69036310437372E-6; 79143/25192
2,64043085284191E-6; 79498/25305
2,59094256440911E-6; 79853/25418
2,54189234444568E-6; 80208/25531
2,49327439727263E-6; 80563/25644
2,44508305443319E-6; 80918/25757
2,39731270401382E-6; 81273/25870
2,34995786132321E-6; 81628/25983
2,30301311234906E-6; 81983/26096
2,25647318443711E-6; 82338/26209
2,21033284734052E-6; 82693/26322
2,16458696976308E-6; 83048/26435
2,1192305193592E-6; 83403/26548
2,0742585485981E-6; 83758/26661
2,02966619476384E-6; 84113/26774
1,9854486516837E-6; 84468/26887
1,94160124040716E-6; 84823/27000
1,89811931025535E-6; 85178/27113
1,85499832363578E-6; 85533/27226
1,81223378536343E-6; 85888/27339
1,76982132747545E-6; 86243/27452
1,72775658200904E-6; 86598/27565
1,6860353223594E-6; 86953/27678
1,64465335019335E-6; 87308/27791
1,60360652372093E-6; 87663/27904
1,5628908142386E-6; 88018/28017
1,52250222131442E-6; 88373/28130
1,48243680105968E-6; 88728/28243
1,44269072267208E-6; 89083/28356
1,40326015534932E-6; 89438/28469
1,36414138137554E-6; 89793/28582
1,32533069717068E-6; 90148/28695
1,28682448396948E-6; 90503/28808
1,24861917954991E-6; 90858/28921
1,21071124996156E-6; 91213/29034
1,1730972602046E-6; 91568/29147
1,13577380355084E-6; 91923/29260
1,09873750154369E-6; 92278/29373
1,06198508881297E-6; 92633/29486
1,02551328585272E-6; 92988/29599
9,89318897971778E-7; 93343/29712
9,53398772886396E-7; 93698/29825
9,17749814856038E-7; 94053/29938
8,82368942275979E-7; 94408/30051
8,47253172492096E-7; 94763/30164
8,12399508714484E-7; 95118/30277
7,77805053103839E-7; 95473/30390
7,4346690782087E-7; 95828/30503
7,09382231569494E-7; 96183/30616
6,75548239596832E-7; 96538/30729
6,4196216128582E-7; 96893/30842
6,08621310834192E-7; 97248/30955
5,75522988303898E-7; 97603/31068
5,42664550300092E-7; 97958/31181
5,10043424106933E-7; 98313/31294
4,7765702287279E-7; 98668/31407
4,45502844560836E-7; 99023/31520
4,13578387134253E-7; 99378/31633
3,81881205099427E-7; 99733/31746
3,50408867098552E-7; 100088/31859
3,19158998317026E-7; 100443/31972
2,88129238076054E-7; 100798/32085
2,57317296375846E-7; 101153/32198
2,26720854945019E-7; 101508/32311
1,96337680326993E-7; 101863/32424
1,66165553200993E-7; 102218/32537
1,36202268382054E-7; 102573/32650
1,06445663092611E-7; 102928/32763
7,68936310983031E-8; 103283/32876
4,75440378931792E-8; 103638/32989
1,83948337860874E-8; 103993/33102
1,05560450499157E-8; 104348/33215
3,89472739745897E-9; 208341/66317
9,27657882316268E-10%; 312689/99532
2,77418946985962E-10%; 833719/265381
5,12666416965132E-11%; 1146408/364913
3,6375309526024E-11%; 3126535/995207
…
Ссылка не открылась, в Википедии есть краткое описание метода Архимеда.
Еще одно доказательство, что Вики — полная ерунда.
Ведь даже школьнику бросится в глаза, что эту дробь еще можно (и нужно!) сократить: 339/108 =113/36.
Ведь даже школьнику бросится в глаза, что эту дробь еще можно (и нужно!) сократить: 339/108 =113/36.
Я не читал Веды в оригинале при подготовке этой статьи, sorry :)
Стало интересно, можно ли вычислить Пи на iPhone
Вот действительно! Тривиальный вопрос, вопрос возникающий сам собой!:)
Если серьезно, у меня возникает вопрос: зачем? Так, просто провести время?)
Есть же вроде алгоритмы, которым пофиг на память, они лупят себе цифры и лупят, не оглядываясь назад
https://en.wikipedia.org/wiki/Pi#Spigot_algorithms
Хоть квинтиллион знаков на своём айфоне считайте
https://en.wikipedia.org/wiki/Pi#Spigot_algorithms
Хоть квинтиллион знаков на своём айфоне считайте
Да, есть алгоритм позволяющий получить любой знак числа Пи без вычисления предыдущих, но в 16-ричной системе счисления. Все равно в десятичную переводить пришлось бы.
вычислил, перевёл, записал в файл, перешёл к следующему знаку?
Пи в 16-ричной системе счисления — это фактически и есть формула Плаффа, приведенная в статье.
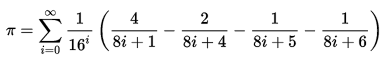
Но мне что-то не приходит в голову, как перевести новый 16-ричный знак в десятичный, не пересчитывая в десятичном виде все число.
Код формулы Плаффа тоже есть в скрипте на питоне под спойлером в статье, кто хочет может поэкспериментировать.
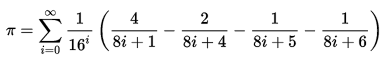
Но мне что-то не приходит в голову, как перевести новый 16-ричный знак в десятичный, не пересчитывая в десятичном виде все число.
Код формулы Плаффа тоже есть в скрипте на питоне под спойлером в статье, кто хочет может поэкспериментировать.
А зачем вообще переводить? Как будто вы потом будете смотреть на этот миллион знаков :)
Можно вычислить 5 шестнадцатеричных знаков и перевести в 8 десятичных.
Для имплементации алгоритма Бэйли—Боруэйна—Плаффа лучше использовать модифицированную версию (её вывел автор в своей работе The BBP Algorithm for Pi):
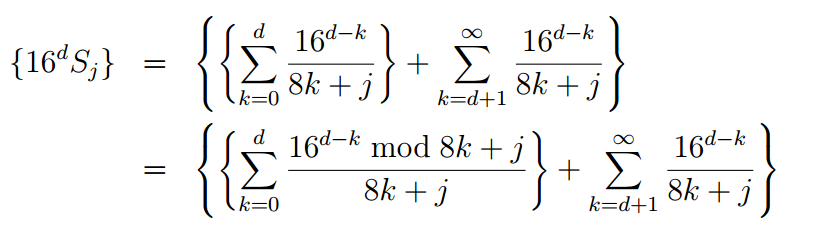
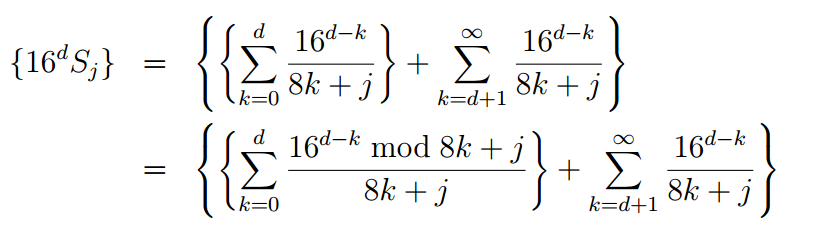
Вас, вероятно, не затруднит ознакомить нас с алгоритмом познакового переведения дробных шестнадцатиричных чисел в десятичные? ;)
https://gist.github.com/getify/fadc109f487067660c38 например таким?
Какой же там стрим? В коде видно:
И обычная глобальная переменная. Т.е. от необходимости хранить результат в памяти (и делить/умножать) мы не избавляемся.
dec = dec + overflow;
var whole = Math.floor(dec);
И обычная глобальная переменная. Т.е. от необходимости хранить результат в памяти (и делить/умножать) мы не избавляемся.
По поводу iOS и как работают программы в фоновом режиме. Когда программа перестает быть активной, её выполнение приостанавливается. Это можно предотвратить, если в этот момент создать UIBackgroundTask и зарегистрировать его в системе. Но этого хватит всего на несколько минут, так как подразумевается завершение какой-то определенной задачи.
Не совсем понял, почему для этого теста нельзя было оставить программу активной на всё время.
Не совсем понял, почему для этого теста нельзя было оставить программу активной на всё время.
Зарегистрируйтесь на Хабре, чтобы оставить комментарий
Вычисление 1000000 знаков числа Пи. На iPhone