В данной статье мы разберем алгоритм консенсуса Паксос, обсудим зачем он нужен, почему работает, докажем его корректность и немного поговорим о проблемах практического применения. Во многом это вольный пересказ статьи Лесли Лампорта «Paxos Made Simple»

Зачастую при работе распределенной системы (попросту несколько серверов обрабатывающих пользовательские запросы или распределенная система хранения данных или что-нибудь еще в этом роде) возникает необходимость принимать общие решения, например на каком из серверов запустить синглетон сервис уровня кластера, и куда его мигрировать при падении этого сервера. Эта задача просто решается при наличии арбитра принимающего решения — админ-сервера. Проблема в том, что арбитр становится единой точкой обрушения, его выход из строя может привести к полной или частичной неработоспособности системы, а его восстановление и восстановление работоспособности системы потребуют ручного вмешательства. Очевидно, что устойчивая к неполадкам система должна состоять из равноправных участников способных договариваться между собой по общим вопросам — достигать консенсуса. Обычно в итоге переговоров выбирают арбитра (используют термины: лидер, мастер) и дальнейшие вопросы, пока он исправен, решают через него.
Лесли Лампорт, изначально хотел математически строго доказать, что консенсус в распределенной системе с ненадежными коммуникациями невозможен, но вместо этого изобрел и доказал алгоритм Паксос (Paxos) позволяющий такого консенсуса достигнуть. Описание алгоритма, с которым можно ознакомиться, например, в википедии выглядит обманчиво простым и коротким, но понять его непросто, а применять на практике еще сложнее.
У данного алгоритма есть важные ограничения: он описывает процесс выбора только одного значения, на практике же нужно принимать множество решений и для каждого следующего случая потребуется создавать новый инстанс алгоритма. Также предполагается, что участники системы ведут себя не по-византийски, т.е. держат свои обещания, не предоставляют ложные данные (историю не знаю, но чувствую — репутация у византийцев была так-себе)
Понятие «выбор» (выбор решения, выбор значения) в контексте алгоритмов консенсуса отличается от бытового. Если в реальной жизни мы сравниваем «за» и «против», то в случае алгоритма консенсуса выбор осуществляется из равнозначных вариантов, т.е. любое значение/решение подойдет, главное — это определиться какое конкретно из множества предложенных.
Это можно сравнить, как вы втроем с друзьями приходите в пиццерию, где вся пицца одинаково хороша (или плоха) и пытаетесь выбрать какую большую пиццу заказать на троих, к вам подходит единственный официант, а вы продолжаете недоуменно смотреть в меню. Из-за соседних столиков начинают подсказывать: «Берите уже Пеппероне, не задерживайте, не хуже чем все остальное» — это было предложение (proposal) и высказал его предлагающий (proposer). Один из вас его расслышал и думает: «окей, пусть будет пепперони». Он — принимающей (acceptor) и только что принял (to accept) предложение. Из-за другого столика кричат: «Вам третий раз говорят — возьмите Маргариту и пусть уже у нас заказ примут» — это ещё одно предложение, а «вам третий раз» — это номер предложения (proposal number), а «Маргарита» — это значение предложения (value). Дальше официант начинает вас опрашивать, кто какие предложения принял. Он — узнающий (leaner) и если большинство (majority) из вас приняло одно и тоже предложение («Я вам третий раз говорю — Маргариту») то это предложение называется выбранным (chosen), и если большинство сообщит его официанту, то официант узнает (to learn) о выбранном значении и сможет принять заказ. Но, скажем, один из принявших то третье предложение залип в смартфон и не реагирует на вопрос официанта.
Значение было выбрано, но узнать его невозможно — оставшиеся в реальном мире двое друзей выдают противоречивые ответы. Начинается следующий раунд переговоров и возможно новое предложение будет принято, а залипший в смартфон участник так и продолжит читать хабр. Так вот, корректный алгоритм консенсуса задает такие правила переговоров, что любое следующее выбранное значение будет совпадать с первый раз выбранным значением.
Таким образом мы разобрались с терминологией и ролями:
На практике роли могут и будут совмещаться, например, если говорить о серверах выбирающих лидера промеж себя, каждый сервер может предложить себя в качестве лидера, будет принимать предложения (в том числе и свои собственные предложения), и в конце-концов ему надо узнать кто же был выбран.
Под большинством понимается «более половины», т.е. N+1 из 2N+1 (и из 2N тоже) или более.
Требование принятия большинством очевидно: если для выбора значения требовалось бы принятие меньшим количеством принимающих (ровно половиной или менее), то ничего бы не мешало выбрать несколько разных значений одновременно, т.е. консенсус бы не был достигнут. Полезным нам окажется тот факт, что любые два множества составляющие большинство имеют непустое пересечение.
При этом не требуется участие всех принимающих в выборе, остальные принимающие могут быть неисправны, связь с ними может быть нарушена. Таким образом мы получаем, что система из 2N+1 участников способна пережить выход из строя N из них.
Мы уже упоминали номер предложения. У каждого предложения (proposal) есть номер. В описании Лампорта это натуральное число такое, что:
Мне помогла в понимании алгоритма следующая аналогия: номер это по-сути таймстамп (timestamp) предложения, вместе таймстампы задают глобальное синтетическое время распределенной системы сконструированное так, что a) никакие два предложения не могут быть сделаны (issued) в один и тот же момент времени, b) можно понять какое из двух предложений сделано «позже». Принимающий приняв какое-то предложение, будет игнорировать предложения, которые были сделаны «раньше» принятого (предложения «из прошлого»).
На практике номер предложения будет состоять из пары: значение счетчика предложений конкретного сервера и идентификатора сервера.
Значение v выбрано, если предложение с номером m и значением v было принято большинством принимающих. После этого любое последующее выбранное значение (принятое большинством принимающих) должно совпадать с выбранным v.
Это требование удастся выполнить, если после того, как значение v было выбрано, принимающие будут принимать только предложения со значениями равными v.
Принимающий принимает то, что предлагающие предлагают и значит предыдущее требование удастся в свою очередь выполнить, если все предлагающие будут во всех предложениях с номером n > m предлагать только выбранное ранее значение v.
Давайте представим будто бы мы доказываем последнее утверждение по индукции и попытаемся понять, чего не хватает, чтобы совершить индукционный переход.
На строгом математическом языке это сформулировано Лампортом так: для осуществления индукционного перехода необходимо чтобы выполнялся следующий инвариант:
Чтобы обеспечить существование описанного выше множества S, предлагающий планирующий сделать предложение n должен узнать у большинства принимающих каковы номер и значение последнего предложения, которое они примут до момента n.
Смотрите в чем проблема: предлагающий может спросить у любого принимающего номер и значение последнего принятого им предложения, но есть шанс, что уже послав ответ принимающий примет следующее предложение и ответ полученный предлагающим будет устаревшим и бесполезным. Чтобы этого избежать Лампорт придумал вот что: пусть предлагающий не только спросит значение последнего принятого предложения, но и попросит не принимать никаких предложений с номером меньшим n. В ответ от принимающего предлагающий получит: 1) значение и номер последнего принятого принимающим предложения и 2) обещание не принимать никакие предложения с номерами меньшими n. Тогда информация о последнем принятом предложении полученная в ответ не устареет, а если будут получены ответы от большинства принимающих, то эти принимающие образуют искомое множество S. Как только множество S сформировано, предлагающий делает предложение (n, v) (где v, как мы обсуждали выше, — это значение последнего предложения (предложения с максимальным номером) принятого принимающими из множества S до момента n).
Таким образом мы получили корректный алгоритм консенсуса, где предложения делаются в два этапа:
Чтобы узнать, что значение было выбрано, узнающий должен увидеть, что одно и тоже предложение (номер плюс значение) было принято большинством принимающих.
Обмен сообщениями асинхронный, коммуникации ненадежные, поэтому неизвестно получит ли предлагающий хоть какие-то ответы, не дождавшись нужного количества обещаний предлагающий повторит попытку сделав уже следующее предложение. Все это может повторяться долго.
Алгоритм не гарантирует, что консенсус будет достигнут. Скажем, один предлагающий получает от большинства обещание не принимать предложения с номером меньше 1, второй в след за ним получает от большинства обещание не принимать предложения с номером меньше 2. Т.е. 1-е предложение теперь не может быть выбрано. Поняв, что его предложение не будет выбрано первый предлагающий постарается получить от большинства обещания не принимать предложения с номером меньше 3. Теперь уже и 2-е предложение не сможет быть принято. И так два предлагающих до бесконечности могут склонять большинство принимающих на одну или другую сторону, блокируя возможность достигнуть консенсус. Это можно исправить введя в алгоритм рандомные задержки, ну и конечно желательно как можно скорее сделать так, чтобы был только один предлагающий. Для этого, когда требуется принимать множественные решения, при выборе следующего значения в качестве предлагающего используют лидера выбранного на предыдущем шаге (в предыдущем инстансе алгоритма).
Но тут возникнет новая проблема: если мы выбрали лидера, ничто не мешает оставшимся узлам за его спиной инициировать новые выборы и выбрать промеж себя другого лидера, у них получится собрать кворум. При этом предыдущий лидер может ничего об этом не знать и будет продолжать действовать считая что он здесь главный.
Другая сложность — это бесчестное византийское поведение и для этого необязательно иметь зловреда в числе элементов системы. Например, принимающие обязаны запомнить свое обещание, для этого они сохраняют его на диск, повреждение данных на диске (из-за сбоя или неаккуратного удаления файлов оператором) приведет к византийскому поведению. На практике даже данные в пямяти могут быть повреждены с тем же печальным итогом. Ошибки в коде тоже могут стать причиной византийского поведения.
Об этих и других проблемах алгоритма Паксос вы можете прочитать в захватывающей статье разработчиков Гугл «Paxos Made Live — An Engineering Perspective», где они рассказывают о своем опыте реализации распределенного консенсуса в проекте Chubby (внутрикорпоративный аналог Zookeeper)
Таким образом алгоритм Паксос — это не серебряная пуля, а всего лишь маленький замечательный фундаментальный кирпичик наших знаний об устойчивых к сбоям распределенных системах.
Зачем нужен распределенный консенсус и что это такое
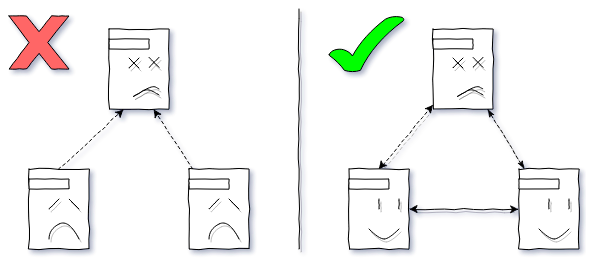
Зачастую при работе распределенной системы (попросту несколько серверов обрабатывающих пользовательские запросы или распределенная система хранения данных или что-нибудь еще в этом роде) возникает необходимость принимать общие решения, например на каком из серверов запустить синглетон сервис уровня кластера, и куда его мигрировать при падении этого сервера. Эта задача просто решается при наличии арбитра принимающего решения — админ-сервера. Проблема в том, что арбитр становится единой точкой обрушения, его выход из строя может привести к полной или частичной неработоспособности системы, а его восстановление и восстановление работоспособности системы потребуют ручного вмешательства. Очевидно, что устойчивая к неполадкам система должна состоять из равноправных участников способных договариваться между собой по общим вопросам — достигать консенсуса. Обычно в итоге переговоров выбирают арбитра (используют термины: лидер, мастер) и дальнейшие вопросы, пока он исправен, решают через него.
Лесли Лампорт, изначально хотел математически строго доказать, что консенсус в распределенной системе с ненадежными коммуникациями невозможен, но вместо этого изобрел и доказал алгоритм Паксос (Paxos) позволяющий такого консенсуса достигнуть. Описание алгоритма, с которым можно ознакомиться, например, в википедии выглядит обманчиво простым и коротким, но понять его непросто, а применять на практике еще сложнее.
У данного алгоритма есть важные ограничения: он описывает процесс выбора только одного значения, на практике же нужно принимать множество решений и для каждого следующего случая потребуется создавать новый инстанс алгоритма. Также предполагается, что участники системы ведут себя не по-византийски, т.е. держат свои обещания, не предоставляют ложные данные (историю не знаю, но чувствую — репутация у византийцев была так-себе)
О выборе и ролях
Понятие «выбор» (выбор решения, выбор значения) в контексте алгоритмов консенсуса отличается от бытового. Если в реальной жизни мы сравниваем «за» и «против», то в случае алгоритма консенсуса выбор осуществляется из равнозначных вариантов, т.е. любое значение/решение подойдет, главное — это определиться какое конкретно из множества предложенных.
Это можно сравнить, как вы втроем с друзьями приходите в пиццерию, где вся пицца одинаково хороша (или плоха) и пытаетесь выбрать какую большую пиццу заказать на троих, к вам подходит единственный официант, а вы продолжаете недоуменно смотреть в меню. Из-за соседних столиков начинают подсказывать: «Берите уже Пеппероне, не задерживайте, не хуже чем все остальное» — это было предложение (proposal) и высказал его предлагающий (proposer). Один из вас его расслышал и думает: «окей, пусть будет пепперони». Он — принимающей (acceptor) и только что принял (to accept) предложение. Из-за другого столика кричат: «Вам третий раз говорят — возьмите Маргариту и пусть уже у нас заказ примут» — это ещё одно предложение, а «вам третий раз» — это номер предложения (proposal number), а «Маргарита» — это значение предложения (value). Дальше официант начинает вас опрашивать, кто какие предложения принял. Он — узнающий (leaner) и если большинство (majority) из вас приняло одно и тоже предложение («Я вам третий раз говорю — Маргариту») то это предложение называется выбранным (chosen), и если большинство сообщит его официанту, то официант узнает (to learn) о выбранном значении и сможет принять заказ. Но, скажем, один из принявших то третье предложение залип в смартфон и не реагирует на вопрос официанта.
Значение было выбрано, но узнать его невозможно — оставшиеся в реальном мире двое друзей выдают противоречивые ответы. Начинается следующий раунд переговоров и возможно новое предложение будет принято, а залипший в смартфон участник так и продолжит читать хабр. Так вот, корректный алгоритм консенсуса задает такие правила переговоров, что любое следующее выбранное значение будет совпадать с первый раз выбранным значением.
Смотрите еще раз, это очень важный и совершенно замечательный момент: состояние системы (принятые значения) распределено по узлам — каждый принимающий знает только о принятом им предложении, общее значение было выбрано, но может возникнуть ситуация, когда узнать его невозможно и даже невозможно узнать было ли что-то выбрано. В этом случае переговоры продолжатся. Но Паксос таков, что любое следующее выбранное большинством принимающих значение будет совпадать с первым выбранным. Выбор, будучи единожды сделан, не будет изменен.
Таким образом мы разобрались с терминологией и ролями:
- Предлагающие — делают предложения.
- Принимающие — принимают предложения, и запоминают принятое (номер и значение). При этом принимающий примет первое поступившие предложение и будет принимать последующие даже если выбор уже сделан.
- Узнающие — узнают какое предложение было выбрано (принято большинством участников).
На практике роли могут и будут совмещаться, например, если говорить о серверах выбирающих лидера промеж себя, каждый сервер может предложить себя в качестве лидера, будет принимать предложения (в том числе и свои собственные предложения), и в конце-концов ему надо узнать кто же был выбран.
О большинстве
Под большинством понимается «более половины», т.е. N+1 из 2N+1 (и из 2N тоже) или более.
Требование принятия большинством очевидно: если для выбора значения требовалось бы принятие меньшим количеством принимающих (ровно половиной или менее), то ничего бы не мешало выбрать несколько разных значений одновременно, т.е. консенсус бы не был достигнут. Полезным нам окажется тот факт, что любые два множества составляющие большинство имеют непустое пересечение.
При этом не требуется участие всех принимающих в выборе, остальные принимающие могут быть неисправны, связь с ними может быть нарушена. Таким образом мы получаем, что система из 2N+1 участников способна пережить выход из строя N из них.
Глобальное время распределенной системы
Мы уже упоминали номер предложения. У каждого предложения (proposal) есть номер. В описании Лампорта это натуральное число такое, что:
- номер уникален, у каждого предложения он свой;
- предлагающий для каждого последующего своего предложения использует больший номер.
Мне помогла в понимании алгоритма следующая аналогия: номер это по-сути таймстамп (timestamp) предложения, вместе таймстампы задают глобальное синтетическое время распределенной системы сконструированное так, что a) никакие два предложения не могут быть сделаны (issued) в один и тот же момент времени, b) можно понять какое из двух предложений сделано «позже». Принимающий приняв какое-то предложение, будет игнорировать предложения, которые были сделаны «раньше» принятого (предложения «из прошлого»).
На практике номер предложения будет состоять из пары: значение счетчика предложений конкретного сервера и идентификатора сервера.
Конструируем корректный алгоритм
Значение v выбрано, если предложение с номером m и значением v было принято большинством принимающих. После этого любое последующее выбранное значение (принятое большинством принимающих) должно совпадать с выбранным v.
Это требование удастся выполнить, если после того, как значение v было выбрано, принимающие будут принимать только предложения со значениями равными v.
Принимающий принимает то, что предлагающие предлагают и значит предыдущее требование удастся в свою очередь выполнить, если все предлагающие будут во всех предложениях с номером n > m предлагать только выбранное ранее значение v.
Давайте представим будто бы мы доказываем последнее утверждение по индукции и попытаемся понять, чего не хватает, чтобы совершить индукционный переход.
Предложение (m, v) — было выбрано, т.е. существует множество C состоящие из большинства принимающих и каждый из этих принимающих принял предложение (m, v). Так же из индукционного предположения следует, что все предложения с номерами из диапазона от m до n-1 включительно имеют значение v (*). Теперь требуется сделать так, чтобы предложение с номер n тоже имело значение v.
Допустим, что существует множество S состоящие из большинства принимающих и такое, что мы можем узнать значение последнего предложения (с максимальным номером меньшим n) принятого принимающими из этого множества. Скажем, номер этого «максимального» предложения — k. Так как множество S содержит хотя бы одного принимающего a из множества C, значит номер k окажется больше либо равен номеру последнего принятого предложения принимающим a, а номер последнего предложения принятого a будет больше либо равен номера m (момента когда значение было выбрано) т.е. k >= m, и таким образом в силу (*) значение предложения k — это выбранное ранее v, будем его использовать чтобы сгенерировать предложение (n, v). Таким образом, если мы сумеем гарантировать существование множеств S, то это обеспечит индукционный переход.
На строгом математическом языке это сформулировано Лампортом так: для осуществления индукционного перехода необходимо чтобы выполнялся следующий инвариант:
Для любых v и n, если предложение (n, v) сделано (issued), то существует множество S состоящее из большинства принимающих и такое, что верно одно из двух: (а) ни один принимающий из множества S не принял ни одного предложения с номером меньше n либо (б) v — это значение предложения с наибольшим номером меньшим n среди всех предложений принятых принимающими из множества S.
Чтобы обеспечить существование описанного выше множества S, предлагающий планирующий сделать предложение n должен узнать у большинства принимающих каковы номер и значение последнего предложения, которое они примут до момента n.
Смотрите в чем проблема: предлагающий может спросить у любого принимающего номер и значение последнего принятого им предложения, но есть шанс, что уже послав ответ принимающий примет следующее предложение и ответ полученный предлагающим будет устаревшим и бесполезным. Чтобы этого избежать Лампорт придумал вот что: пусть предлагающий не только спросит значение последнего принятого предложения, но и попросит не принимать никаких предложений с номером меньшим n. В ответ от принимающего предлагающий получит: 1) значение и номер последнего принятого принимающим предложения и 2) обещание не принимать никакие предложения с номерами меньшими n. Тогда информация о последнем принятом предложении полученная в ответ не устареет, а если будут получены ответы от большинства принимающих, то эти принимающие образуют искомое множество S. Как только множество S сформировано, предлагающий делает предложение (n, v) (где v, как мы обсуждали выше, — это значение последнего предложения (предложения с максимальным номером) принятого принимающими из множества S до момента n).
Таким образом мы получили корректный алгоритм консенсуса, где предложения делаются в два этапа:
- Подготовительный этап:
- Предлагающий рассылает анонс, что он планирует сделать предложение n (в момент времени n)
- Принимающие получившие анонс посылают в ответ обещание не принимать никаких предложений с номерами меньшими n (до момента n), а также последнее принятое предложение (номер и значение) или не отвечают вовсе, если номер последнего принятого принимающим предложения превосходит n или если n входит в число предложений, которые принимающий уже пообещал не принимать другому предлагающему.
- Предложение:
- Предлагающий получив ответы от большинства принимающих выбирает в качестве значения предложения v значение из ответа с максимальным номером предложения и рассылает предложение (n, v).
- Принимающий, получив предложение (n, v), обязан принять его если он, конечно, не пообещал другому предлагающему не принимать предложений с номерами меньшими n*, где n* > n.
Чтобы узнать, что значение было выбрано, узнающий должен увидеть, что одно и тоже предложение (номер плюс значение) было принято большинством принимающих.
Проблемы практического применения
Обмен сообщениями асинхронный, коммуникации ненадежные, поэтому неизвестно получит ли предлагающий хоть какие-то ответы, не дождавшись нужного количества обещаний предлагающий повторит попытку сделав уже следующее предложение. Все это может повторяться долго.
Алгоритм не гарантирует, что консенсус будет достигнут. Скажем, один предлагающий получает от большинства обещание не принимать предложения с номером меньше 1, второй в след за ним получает от большинства обещание не принимать предложения с номером меньше 2. Т.е. 1-е предложение теперь не может быть выбрано. Поняв, что его предложение не будет выбрано первый предлагающий постарается получить от большинства обещания не принимать предложения с номером меньше 3. Теперь уже и 2-е предложение не сможет быть принято. И так два предлагающих до бесконечности могут склонять большинство принимающих на одну или другую сторону, блокируя возможность достигнуть консенсус. Это можно исправить введя в алгоритм рандомные задержки, ну и конечно желательно как можно скорее сделать так, чтобы был только один предлагающий. Для этого, когда требуется принимать множественные решения, при выборе следующего значения в качестве предлагающего используют лидера выбранного на предыдущем шаге (в предыдущем инстансе алгоритма).
Но тут возникнет новая проблема: если мы выбрали лидера, ничто не мешает оставшимся узлам за его спиной инициировать новые выборы и выбрать промеж себя другого лидера, у них получится собрать кворум. При этом предыдущий лидер может ничего об этом не знать и будет продолжать действовать считая что он здесь главный.
Другая сложность — это бесчестное византийское поведение и для этого необязательно иметь зловреда в числе элементов системы. Например, принимающие обязаны запомнить свое обещание, для этого они сохраняют его на диск, повреждение данных на диске (из-за сбоя или неаккуратного удаления файлов оператором) приведет к византийскому поведению. На практике даже данные в пямяти могут быть повреждены с тем же печальным итогом. Ошибки в коде тоже могут стать причиной византийского поведения.
Об этих и других проблемах алгоритма Паксос вы можете прочитать в захватывающей статье разработчиков Гугл «Paxos Made Live — An Engineering Perspective», где они рассказывают о своем опыте реализации распределенного консенсуса в проекте Chubby (внутрикорпоративный аналог Zookeeper)
Таким образом алгоритм Паксос — это не серебряная пуля, а всего лишь маленький замечательный фундаментальный кирпичик наших знаний об устойчивых к сбоям распределенных системах.








