Как стать автором
Поиск
Написать публикацию
Обновить

Оптимизация настроек ПИД регулятора по интегральному критерию качества регулирования

Время на прочтение12 мин
Количество просмотров12K
Python*Алгоритмы*Анализ и проектирование систем*Математика*Разработка под Windows*
Туториал


Постановка задачи оценки качества регулирования


Интегральные оценки качества регулирования характеризует суммарное отклонение реального переходного процесса в системе от идеализированного переходного процесса.

В качестве идеализированного процесса обычно принимается ступенчатый (скачкообразный) переходный процесс или экспоненциальный процесс с заданными параметрами экспоненты.

До настоящего времени остаётся не выясненным, какой из интегральных критериев линейный или квадратичный выбрать для оптимизации настроек регуляторов.

В данной публикации определение оптимальных настроек регулятора осуществляется на основе критерия оптимальности в виде суммы линейного и квадратичного интегральных показателей качества регулирования.

Чтобы осуществить такой выбор, вначале необходимо провести серию предварительных расчетов для различных значений отношения постоянных времени дифференцирования и интегрирования α=Td/Ti и выбрать несколько значений α, которые обеспечивает наибольшее значение отношения Kr/Ki.

После этого, имея несколько вариантов настроек регулятора, построить для них переходные процессы в замкнутой системе и по предложенному критерию отобрать оптимальные настройки.

Программная реализация расчёта оптимальных настроек регулятора


Расчёт можно выполнить как в математическом пакете, так и на любом языке программирования. Однако, по причине наличия мощных библиотек для численного интегрирования и простой реализации поиска локальных экстремумов в списках, я выбрал высокоуровневый язык программирования Python.

Для упрощения поисковых процедур в начале программы целесообразно установить исходные данные и привести готовые списки частот отдельно для каждой решаемой задачи:

Подготовка исходных данных
# -*- coding: utf8 -*-    
import numpy as np # модуль для работы со списками
from scipy.integrate import quad # модуль для численного  интегрирования
import matplotlib.pyplot as plt # модуль для построения графиков
T1=14; T2=18; T3=28; K=0.9; tau=6.4# Постоянные времени, коэффициент усиления, запаздывание
m=0.366; m1=0.221# Запас устойчивости
n= np.arange(0.001,0.15,0.0002)# Список частот для плоскости Kr-Ki
n1=np.arange(0.00001,0.12,0.0001) # Список частот для графика Ki=f(w)
n2=np.arange(0.0002,0.4,0.0001) #Массив частот для построения АЧХ


Вводим передаточную функцию для водяного теплообменника с учётом корневого показателя колебательности m и передаточную функцию ПИД регулятора с учётом Kr, Ti, Td, остальные функции вспомогательные:

Ввод основных и вспомогательных функций с учётом комплексной арифметики
def WO(m,w):#Передаточная функция объекта
         j=(-1)**0.5
         return K*np.exp(-tau*(-m+j)*w)/((T1*(-m+j)*w+1)*(T2*(-m+j)*w+1)*(T3*(-m+j)*w+1))
def WR(w,Kr,Ti,Td):#Передаточная функция регулятора
         j=(-1)**0.5
         return Kr*(1+1/(j*w*Ti)+j*w*Td)
def ReW(m,w):#Действительная часть передаточной функции
          j=(-1)**0.5
          return WO(m,w).real
def ImW(m,w):#Мнимая часть передаточной функции
          j=(-1)**0.5
          return WO(m,w).imag
def A0(m,w):#Вспомогательная функция
         return -(ImW(m,w)*m/(w+w*m**2)+ReW(m,w)/(w+w*m**2))
def Ti(alfa,m,w):#Коэффициент регулятора
         return  (-ImW(m,w)-(ImW(m,w)**2-4*((ReW(m,w)*alfa*w-ImW(m,w)*alfa*w*m)*A0(m,w)))**0.5)/(2*(ReW(m,w)*alfa*w-ImW(m,w)*alfa*w*m))
def Ki(alfa,m,w):#Коэффициент регулятора
         return 1/(w*Ti(alfa,m,w)**2*alfa*(m*ReW(m,w)+ImW(m,w))-Ti(alfa,m,w)*ReW(m,w)+(m*ReW(m,w)-ImW(m,w))/(w+w*m**2))
def Kr(alfa,m,w):#Коэффициент регулятора
         if Ki(alfa,m,w)*Ti(alfa,m,w)<0:
                  z=0
         else:
                  z=Ki(alfa,m,w)*Ti(alfa,m,w)
         return z         
def Kd(alfa,m,w):#Коэффициент регулятора
         return alfa*Kr(alfa,m,w)*Ti(alfa,m,w)


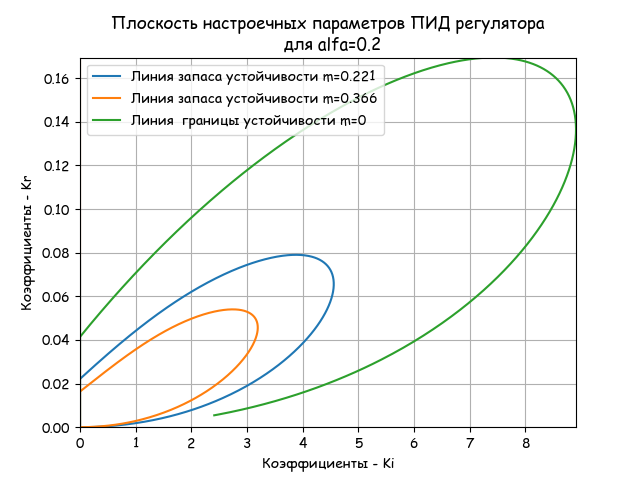
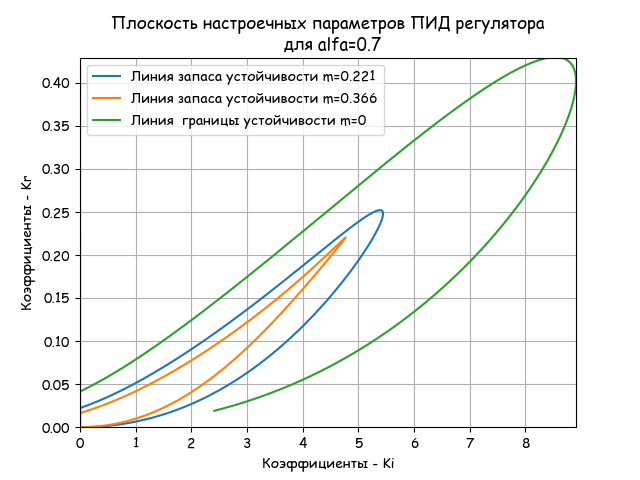
Построим три плоскости настройки ПИД регулятора для отношений alfa=Td/Ti=0.2,alfa=Td/Ti=0.7 alfa=Td/Ti=1.2.

Поиск оптимальных значений alfa
alfa=0.2
Ki_1=[Ki(alfa,m1,w) for w in n]
Kr_1=[Kr(alfa,m1,w) for w in n]
Ki_2=[Ki(alfa,m,w) for w in n]
Kr_2=[Kr(alfa,m,w) for w in n]
Ki_3=[Ki(alfa,0,w) for w in n]
Kr_3=[Kr(alfa,0,w) for w in n]    
plt.figure()
plt.title("Плоскость настроечных параметров ПИД регулятора\n  для alfa=%s"%alfa)
plt.axis([0.0, round(max(Kr_3),4), 0.0, round(max(Ki_3),4)])
plt.plot(Kr_1, Ki_1, label='Линия запаса устойчивости m=%s'%m1)
plt.plot(Kr_2, Ki_2, label='Линия запаса устойчивости m=%s'%m)
plt.plot(Kr_3, Ki_3, label='Линия  границы устойчивости m=0')
plt.xlabel("Коэффициенты - Ki")
plt.ylabel("Коэффициенты - Kr")
plt.legend(loc='best')
plt.grid(True)
alfa=0.7
Ki_1=[Ki(alfa,0.221,w) for w in n]
Kr_1=[Kr(alfa,0.221,w) for w in n]
Ki_2=[Ki(alfa,0.366,w) for w in n]
Kr_2=[Kr(alfa,0.366,w) for w in n]
Ki_3=[Ki(alfa,0,w) for w in n]
Kr_3=[Kr(alfa,0,w) for w in n]
plt.figure()
plt.axis([0.0, round(max(Kr_3),3), 0.0, round(max(Ki_3),3)])
plt.title("Плоскость настроечных параметров ПИД регулятора\n  для alfa=%s"%alfa)
plt.plot(Kr_1, Ki_1, label='Линия запаса устойчивости m=%s'%m1)
plt.plot(Kr_2, Ki_2, label='Линия запаса устойчивости m=%s'%m)
plt.plot(Kr_3, Ki_3, label='Линия  границы устойчивости m=0')
plt.xlabel("Коэффициенты - Ki")
plt.ylabel("Коэффициенты - Kr")
plt.legend(loc='best')
plt.grid(True)
alfa=1.2
Ki_1=[Ki(alfa,0.221,w) for w in n]
Kr_1=[Kr(alfa,0.221,w) for w in n]
Ki_2=[Ki(alfa,0.366,w) for w in n]
Kr_2=[Kr(alfa,0.366,w) for w in n]
Ki_3=[Ki(alfa,0,w) for w in n]
Kr_3=[Kr(alfa,0,w) for w in n]
plt.figure()
plt.title("Плоскость настроечных параметров ПИД регулятора\n  для alfa=%s"%alfa)
plt.axis([0.0, round(max(Kr_3),3), 0.0, round(max(Ki_3),3)])
plt.plot(Kr_1, Ki_1, label='Линия запаса устойчивости m=%s'%m1)
plt.plot(Kr_2, Ki_2, label='Линия запаса устойчивости m=%s'%m)
plt.plot(Kr_3, Ki_3, label='Линия  границы устойчивости m=0')
plt.xlabel("Коэффициенты - Ki")
plt.ylabel("Коэффициенты - Kr")
plt.legend(loc='best')
plt.grid(True)
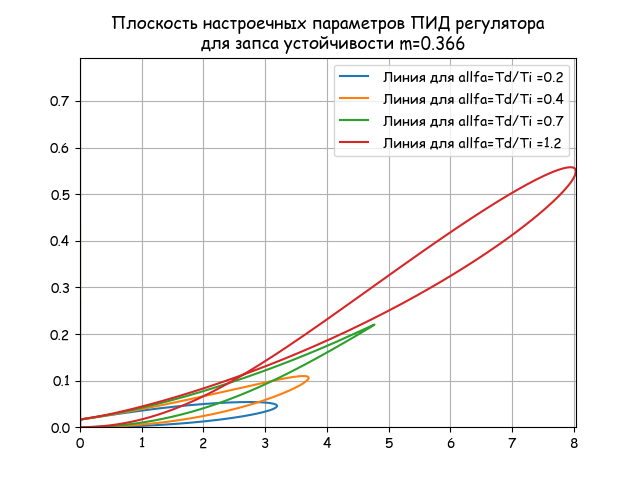
plt.figure(
)

Для запаса устойчивости m=0.386 при значениях alfa -0.2,0,4,0.7 построим D –разбиения для определения критических значения alfa.

Общая плоскость всех настроечных параметров
plt.title("Плоскость настроечных параметров ПИД регулятора\n  для запаса устойчивости m=%s"%m)
alfa=0.2
Ki_2=[Ki(alfa,m,w) for w in n]
Kr_2=[Kr(alfa,m,w) for w in n]
plt.plot(Kr_2, Ki_2,label=' Линия для allfa=Td/Ti =%s'%alfa)
alfa=0.4
Ki_2=[Ki(alfa,m,w) for w in n]
Kr_2=[Kr(alfa,m,w) for w in n]
plt.plot(Kr_2, Ki_2,label=' Линия для allfa=Td/Ti =%s'%alfa)
alfa=0.7
Ki_2=[Ki(alfa,m,w) for w in n]
Kr_2=[Kr(alfa,m,w) for w in n]
plt.plot(Kr_2, Ki_2,label=' Линия для allfa=Td/Ti =%s'%alfa)
alfa=1.2
Ki_2=[Ki(alfa,m,w) for w in n]
Kr_2=[Kr(alfa,m,w) for w in n]
plt.plot(Kr_2, Ki_2,label=' Линия для allfa=Td/Ti =%s'%alfa)
plt.axis([0.0, round(max(Kr_2),3), 0.0, round(max(Ki_2),3)])
plt.legend(loc='best')
plt.grid(True)


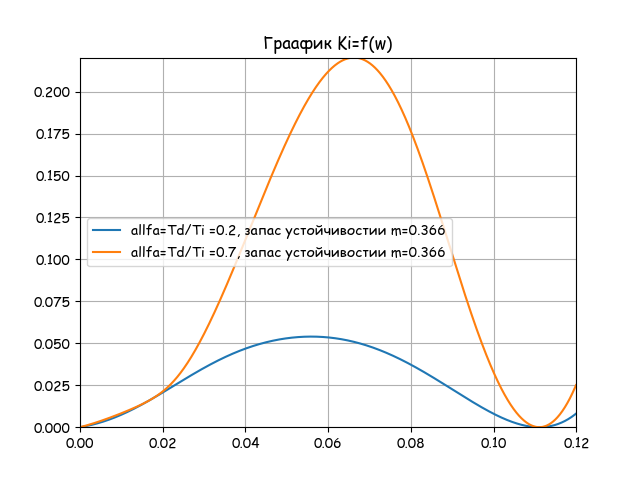
Строим график зависимости Ki от частоты w для двух выявленных из предыдущего графика значений alfa: 0.2; 0.7. Настройки Ki определяются по резонансным частотам.

plt.figure()
plt.title("График Ki=f(w)")
Ki_1=[Ki(0.2,m,w) for w in n1]
Ki_2=[Ki(0.7,m,w) for w in n1]
Ky=max([round(max(Ki_1),4),round(max(Ki_2),4)])
plt.axis([0.0,round(max(n1),4),0.0, Ky])
plt.plot(n1, Ki_1,label='allfa=Td/Ti =0.2, запас устойчивости m=0.366')
plt.plot(n1, Ki_2,label='allfa=Td/Ti =0.7, запас устойчивости m=0.366')
plt.legend(loc='best')
plt.grid(True)

Определяем три варианта настроек ПИД регулятора:

Получение численных значений настроек для выбора оптимальных по предложенному критерию
maxKi=max( [Ki(0.7,m,w) for w in n1])
wa=round([w for w in n1 if Ki(0.7,m,w)==maxKi][0],3)
Ki1=round(Ki(0.7,m,wa),3)
Kr1=round(Kr(0.7,m,wa),3)
Ti1=round(Kr1/Ki1,3)
Td1=round(0.7*Ti1,3)
d=[]
d[0]= "Настройки №1 ПИД регулятора (wa =%s,m=0.366,alfa=0.7): Kr=%s; Ti=%s; Ki=%s; Td=%s "%(wa,Kr1,Ti1,Ki1,Td1)
print(d[0])
maxKi=max( [Ki(0.2,m,w) for w in n1])
wa=round([w for w in n1 if Ki(0.2,m,w)==maxKi][0],3)
Ki2=round(Ki(0.2,m,wa),3)
Kr2=round(Kr(0.2,m,wa),3)
Ti2=round(Kr2/Ki2,3)
Td2=round(0.2*Ti2,3)
d[1]= "Настройки №2 ПИД регулятора(wa =%s,m=0.366,alfa=0.2): Kr=%s; Ti=%s; Ki=%s; Td=%s "%(wa,Kr2,Ti2,Ki2,Td2)
print(d[1])
wa=fsolve(lambda w:Ki(0.7,m,w)-0.14,0.07)[0]
wa=round(wa,3)
Ki3=round(Ki(0.7,m,wa),3)
Kr3=round(Kr(0.7,m,wa),3)
Ti3=round(Kr3/Ki3,3)
Td3=round(0.7*Ti3,3)
d[2]= ("Настройки №3 ПИД регулятора(wa =%s,m=0.366,alfa=0.7): Kr=%s; Ti=%s; Ki=%s; Td=%s "%(wa,Kr3,Ti3,Ki3,Td3)
print(d[2])
def Wsys(w,Kr,Ti,Td):
         j=(-1)**0.5
         return (WO(0,w)*WR(w,Kr,Ti,Td)/(1+WO(0,w)*WR(w,Kr,Ti,Td)))
Wsys_1=[abs(Wsys(w,Kr1,Ti1,Td1)) for w in n2]
Wsys_2=[abs(Wsys(w,Kr2,Ti2,Td2)) for w in n2]
Wsys_3=[abs(Wsys(w,Kr3,Ti3,Td3)) for w in n2]
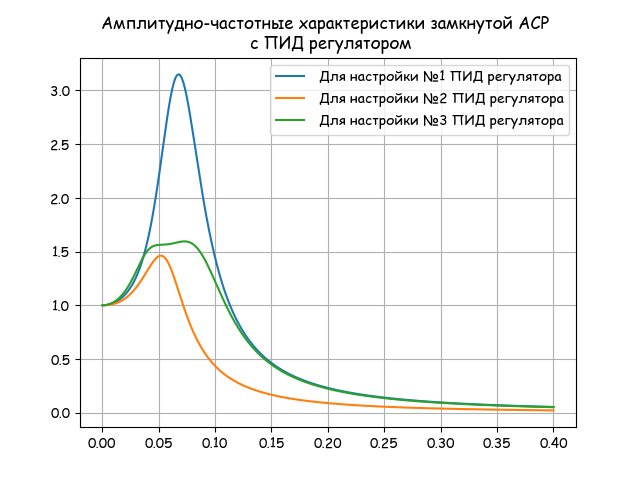
plt.figure()


Определяем динамику АСР по значению частотного показателя колебательности:

plt.title("Амплитудно-частотные характеристики замкнутой АСР \n с ПИД регулятором")
plt.plot(n2, Wsys_1,label=' Для настройки №1 ПИД регулятора')
plt.plot(n2, Wsys_2,label=' Для настройки №2 ПИД регулятора')
plt.plot(n2, Wsys_3,label=' Для настройки №3 ПИД регулятора')
plt.legend(loc='best')
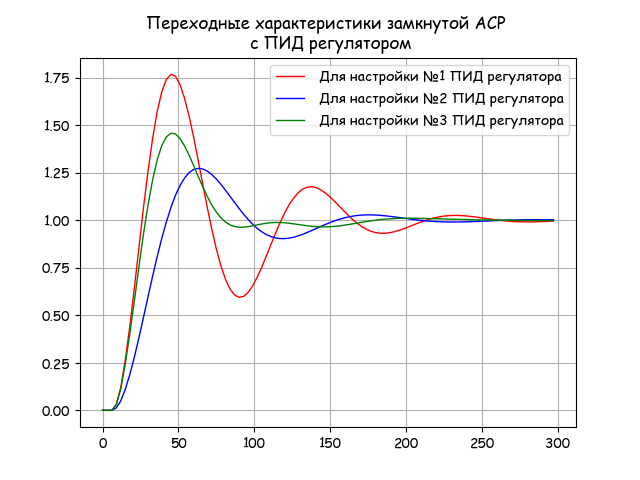
plt.grid(True)

Определяем оптимальные настройки регулятора по предложенному интегральному критерию качества регулирования:



Численный и графический анализ оптимальности полученных настроек
def ReWsys(w,t,Kr,Ti,Td):
         return(2/np.pi)* (WO(0,w)*WR(w,Kr,Ti,Td)/(1+WO(0,w)*WR(w,Kr,Ti,Td))).real*(np.sin(w*t)/w)
def h(t,Kr,Ti,Td):
         return quad(lambda w: ReWsys(w,t,Kr,Ti,Td),0,0.6)[0] 
tt=np.arange(0,300,3)
h1=[h(t,Kr1,Ti1,Td1) for t in tt]
h2=[h(t,Kr2,Ti2,Td2) for t in tt]
h3=[h(t,Kr3,Ti3,Td3) for t in tt]
I1=round(quad(lambda t: h(t,Kr1,Ti1,Td1), 0,200)[0],3)
I11=round(quad(lambda t: h(t,Kr1,Ti1,Td1)**2,0, 200)[0],3)
I2=round(quad(lambda t: h(t,Kr2,Ti2,Td2), 0,200)[0],3)
I21=round(quad(lambda t: h(t,Kr2,Ti2,Td2)**2,0, 200)[0],3)
I3=round(quad(lambda t: h(t,Kr3,Ti3,Td3), 0,200)[0],3)
I31=round(quad(lambda t: h(t,Kr3,Ti3,Td3)**2,0, 200)[0],3)
print("Линейный интегральный  критерий качества I1 =%s (настройки №1)"%I1)
print("Квадратичный интегральный  критерий качества I2 =%s (настройки №1"%I11)
print("Линейный интегральный критерий качества I1 =%s (настройки №2 )"%I2)
print("Квадратичный интегральный критерий качества I2 =%s (настройки №2)"%I21)
print("Линейный интегральный критерий качества I1 =%s (настройки №3 )"%I3)
print("Квадратичный интегральный критерий качества I2 =%s (настройки №3)"%I31)
Rez=[I1+I11,I2+I21,I3+I31]
In=Rez.index(min(Rez))
print("Оптимальные параметры по интегральным критериям :\n %s"%d[In])
plt.figure()
plt.title("Переходные характеристики замкнутой АСР \n с ПИД регулятором")
plt.plot(tt,h1,'r',linewidth=1,label=' Для настройки №1 ПИД регулятора')
plt.plot(tt,h2,'b',linewidth=1,label=' Для настройки №2 ПИД регулятора')
plt.plot(tt,h3,'g',linewidth=1,label=' Для настройки №3 ПИД регулятора')
plt.legend(loc='best')
plt.grid(True)
plt.show()


Результат работы программы –текстовый вывод:

Настройки №1 ПИД регулятора (wa =0.066,m=0.366,alfa=0.7): Kr=4.77; Ti=21.682; Ki=0.22; Td=15.177
Настройки №2 ПИД регулятора(wa =0.056,m=0.366,alfa=0.2): Kr=2.747; Ti=50.87; Ki=0.054; Td=10.174
Настройки №3 ПИД регулятора(wa =0.085,m=0.366,alfa=0.7): Kr=3.747; Ti=26.387; Ki=0.142; Td=18.471
Линейный интегральный критерий качества I1 =194.65 (настройки №1)
Квадратичный интегральный критерий качества I2 =222.428 (настройки №1
Линейный интегральный критерий качества I1 =179.647 (настройки №2 )
Квадратичный интегральный критерий качества I2 =183.35 (настройки №2)
Линейный интегральный критерий качества I1 =191.911 (настройки №3 )
Квадратичный интегральный критерий качества I2 =204.766 (настройки №3)
Оптимальные параметры по интегральным критериям:
Настройки №2 ПИД регулятора(wa =0.056,m=0.366,alfa=0.2): Kr=2.747; Ti=50.87; Ki=0.054; Td=10.174

Результат работы программы, графический вывод:















Полный текст программы
# -*- coding: utf8 -*-    
import numpy as np
from scipy.integrate import quad
from scipy.optimize import *
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['font.family'] = 'fantasy'
mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial'
T1=14;T2=18;T3=28;K=0.9;tau=6.4# Постоянные времени, коэффициент, запаздывание
m=0.366;m1=0.221# Запас устойчивости
n= np.arange(0.001,0.15,0.0002)#Массив частот для плоскости Kr-Ki
n1=np.arange(0.00001,0.12,0.0001)#Массив частот для графика Ki=f(w)
n2=np.arange(0.0002,0.4,0.0001)#Массив частот для построения АЧХ
def WO(m,w):#Передаточная функция объекта
         j=(-1)**0.5
         return K*np.exp(-tau*(-m+j)*w)/((T1*(-m+j)*w+1)*(T2*(-m+j)*w+1)*(T3*(-m+j)*w+1))
def WR(w,Kr,Ti,Td):#Передаточная функция регулятора
         j=(-1)**0.5
         return Kr*(1+1/(j*w*Ti)+j*w*Td)
def ReW(m,w):#Действительная часть передаточной функции
          j=(-1)**0.5
          return WO(m,w).real
def ImW(m,w):#Мнимая часть передаточной функции
          j=(-1)**0.5
          return WO(m,w).imag
def A0(m,w):#Вспомогательная функция
         return -(ImW(m,w)*m/(w+w*m**2)+ReW(m,w)/(w+w*m**2))
def Ti(alfa,m,w):#Коэффициент регулятора
         return  (-ImW(m,w)-(ImW(m,w)**2-4*((ReW(m,w)*alfa*w-ImW(m,w)*alfa*w*m)*A0(m,w)))**0.5)/(2*(ReW(m,w)*alfa*w-ImW(m,w)*alfa*w*m))
def Ki(alfa,m,w):#Коэффициент регулятора
         return 1/(w*Ti(alfa,m,w)**2*alfa*(m*ReW(m,w)+ImW(m,w))-Ti(alfa,m,w)*ReW(m,w)+(m*ReW(m,w)-ImW(m,w))/(w+w*m**2))
def Kr(alfa,m,w):#Коэффициент регулятора
         if Ki(alfa,m,w)*Ti(alfa,m,w)<0:
                  z=0
         else:
                  z=Ki(alfa,m,w)*Ti(alfa,m,w)
         return z         
def Kd(alfa,m,w):#Коэффициент регулятора
         return alfa*Kr(alfa,m,w)*Ti(alfa,m,w)
alfa=0.2
Ki_1=[Ki(alfa,m1,w) for w in n]
Kr_1=[Kr(alfa,m1,w) for w in n]
Ki_2=[Ki(alfa,m,w) for w in n]
Kr_2=[Kr(alfa,m,w) for w in n]
Ki_3=[Ki(alfa,0,w) for w in n]
Kr_3=[Kr(alfa,0,w) for w in n]    
plt.figure()
plt.title("Плоскость настроечных параметров ПИД регулятора\n  для alfa=%s"%alfa)
plt.axis([0.0, round(max(Kr_3),4), 0.0, round(max(Ki_3),4)])
plt.plot(Kr_1, Ki_1, label='Линия запаса устойчивости m=%s'%m1)
plt.plot(Kr_2, Ki_2, label='Линия запаса устойчивости m=%s'%m)
plt.plot(Kr_3, Ki_3, label='Линия  границы устойчивости m=0')
plt.xlabel("Коэффициенты - Ki")
plt.ylabel("Коэффициенты - Kr")
plt.legend(loc='best')
plt.grid(True)
alfa=0.7
Ki_1=[Ki(alfa,0.221,w) for w in n]
Kr_1=[Kr(alfa,0.221,w) for w in n]
Ki_2=[Ki(alfa,0.366,w) for w in n]
Kr_2=[Kr(alfa,0.366,w) for w in n]
Ki_3=[Ki(alfa,0,w) for w in n]
Kr_3=[Kr(alfa,0,w) for w in n]
plt.figure()
plt.axis([0.0, round(max(Kr_3),3), 0.0, round(max(Ki_3),3)])
plt.title("Плоскость настроечных параметров ПИД регулятора\n  для alfa=%s"%alfa)
plt.plot(Kr_1, Ki_1, label='Линия запаса устойчивости m=%s'%m1)
plt.plot(Kr_2, Ki_2, label='Линия запаса устойчивости m=%s'%m)
plt.plot(Kr_3, Ki_3, label='Линия  границы устойчивости m=0')
plt.xlabel("Коэффициенты - Ki")
plt.ylabel("Коэффициенты - Kr")
plt.legend(loc='best')
plt.grid(True)
alfa=1.2
Ki_1=[Ki(alfa,0.221,w) for w in n]
Kr_1=[Kr(alfa,0.221,w) for w in n]
Ki_2=[Ki(alfa,0.366,w) for w in n]
Kr_2=[Kr(alfa,0.366,w) for w in n]
Ki_3=[Ki(alfa,0,w) for w in n]
Kr_3=[Kr(alfa,0,w) for w in n]
plt.figure()
plt.title("Плоскость настроечных параметров ПИД регулятора\n  для alfa=%s"%alfa)
plt.axis([0.0, round(max(Kr_3),3), 0.0, round(max(Ki_3),3)])
plt.plot(Kr_1, Ki_1, label='Линия запаса устойчивости m=%s'%m1)
plt.plot(Kr_2, Ki_2, label='Линия запаса устойчивости m=%s'%m)
plt.plot(Kr_3, Ki_3, label='Линия  границы устойчивости m=0')
plt.xlabel("Коэффициенты - Ki")
plt.ylabel("Коэффициенты - Kr")
plt.legend(loc='best')
plt.grid(True)
plt.figure()
plt.title("Плоскость настроечных параметров ПИД регулятора\n  для запаса устойчивости m=%s"%m)
alfa=0.2
Ki_2=[Ki(alfa,m,w) for w in n]
Kr_2=[Kr(alfa,m,w) for w in n]
plt.plot(Kr_2, Ki_2,label=' Линия для allfa=Td/Ti =%s'%alfa)
alfa=0.4
Ki_2=[Ki(alfa,m,w) for w in n]
Kr_2=[Kr(alfa,m,w) for w in n]
plt.plot(Kr_2, Ki_2,label=' Линия для allfa=Td/Ti =%s'%alfa)
alfa=0.7
Ki_2=[Ki(alfa,m,w) for w in n]
Kr_2=[Kr(alfa,m,w) for w in n]
plt.plot(Kr_2, Ki_2,label=' Линия для allfa=Td/Ti =%s'%alfa)
alfa=1.2
Ki_2=[Ki(alfa,m,w) for w in n]
Kr_2=[Kr(alfa,m,w) for w in n]
plt.plot(Kr_2, Ki_2,label=' Линия для allfa=Td/Ti =%s'%alfa)
plt.axis([0.0, round(max(Kr_2),3), 0.0, round(max(Ki_2),3)])
plt.legend(loc='best')
plt.grid(True)
plt.figure()
plt.title("График Ki=f(w)")
Ki_1=[Ki(0.2,m,w) for w in n1]
Ki_2=[Ki(0.7,m,w) for w in n1]
Ky=max([round(max(Ki_1),4),round(max(Ki_2),4)])
plt.axis([0.0,round(max(n1),4),0.0, Ky])
plt.plot(n1, Ki_1,label='allfa=Td/Ti =0.2, запас устойчивости m=0.366')
plt.plot(n1, Ki_2,label='allfa=Td/Ti =0.7, запас устойчивости m=0.366')
plt.legend(loc='best')
plt.grid(True)
maxKi=max( [Ki(0.7,m,w) for w in n1])
wa=round([w for w in n1 if Ki(0.7,m,w)==maxKi][0],3)
Ki1=round(Ki(0.7,m,wa),3)
Kr1=round(Kr(0.7,m,wa),3)
Ti1=round(Kr1/Ki1,3)
Td1=round(0.7*Ti1,3)
d={}
d[0]= "Настройки №1 ПИД регулятора (wa =%s,m=0.366,alfa=0.7): Kr=%s; Ti=%s; Ki=%s; Td=%s "%(wa,Kr1,Ti1,Ki1,Td1)
print(d[0])
maxKi=max( [Ki(0.2,m,w) for w in n1])
wa=round([w for w in n1 if Ki(0.2,m,w)==maxKi][0],3)
Ki2=round(Ki(0.2,m,wa),3)
Kr2=round(Kr(0.2,m,wa),3)
Ti2=round(Kr2/Ki2,3)
Td2=round(0.2*Ti2,3)
d[1]= "Настройки №2 ПИД регулятора(wa =%s,m=0.366,alfa=0.2): Kr=%s; Ti=%s; Ki=%s; Td=%s "%(wa,Kr2,Ti2,Ki2,Td2)
print(d[1])
wa=fsolve(lambda w:Ki(0.7,m,w)-0.14,0.07)[0]
wa=round(wa,3)
Ki3=round(Ki(0.7,m,wa),3)
Kr3=round(Kr(0.7,m,wa),3)
Ti3=round(Kr3/Ki3,3)
Td3=round(0.7*Ti3,3)
d[2]= "Настройки №3 ПИД регулятора(wa =%s,m=0.366,alfa=0.7): Kr=%s; Ti=%s; Ki=%s; Td=%s "%(wa,Kr3,Ti3,Ki3,Td3)
print(d[2])
def Wsys(w,Kr,Ti,Td):
         j=(-1)**0.5
         return (WO(0,w)*WR(w,Kr,Ti,Td)/(1+WO(0,w)*WR(w,Kr,Ti,Td)))
Wsys_1=[abs(Wsys(w,Kr1,Ti1,Td1)) for w in n2]
Wsys_2=[abs(Wsys(w,Kr2,Ti2,Td2)) for w in n2]
Wsys_3=[abs(Wsys(w,Kr3,Ti3,Td3)) for w in n2]
plt.figure()
plt.title("Амплитудно-частотные характеристики замкнутой АСР \n с ПИД регулятором")
plt.plot(n2, Wsys_1,label=' Для настройки №1 ПИД регулятора')
plt.plot(n2, Wsys_2,label=' Для настройки №2 ПИД регулятора')
plt.plot(n2, Wsys_3,label=' Для настройки №3 ПИД регулятора')
plt.legend(loc='best')
plt.grid(True)
def ReWsys(w,t,Kr,Ti,Td):
         return(2/np.pi)* (WO(0,w)*WR(w,Kr,Ti,Td)/(1+WO(0,w)*WR(w,Kr,Ti,Td))).real*(np.sin(w*t)/w)
def h(t,Kr,Ti,Td):
         return quad(lambda w: ReWsys(w,t,Kr,Ti,Td),0,0.6)[0] 
tt=np.arange(0,300,3)
h1=[h(t,Kr1,Ti1,Td1) for t in tt]
h2=[h(t,Kr2,Ti2,Td2) for t in tt]
h3=[h(t,Kr3,Ti3,Td3) for t in tt]
I1=round(quad(lambda t: h(t,Kr1,Ti1,Td1), 0,200)[0],3)
I11=round(quad(lambda t: h(t,Kr1,Ti1,Td1)**2,0, 200)[0],3)
I2=round(quad(lambda t: h(t,Kr2,Ti2,Td2), 0,200)[0],3)
I21=round(quad(lambda t: h(t,Kr2,Ti2,Td2)**2,0, 200)[0],3)
I3=round(quad(lambda t: h(t,Kr3,Ti3,Td3), 0,200)[0],3)
I31=round(quad(lambda t: h(t,Kr3,Ti3,Td3)**2,0, 200)[0],3)
print("Линейный интегральный  критерий качества I1 =%s (настройки №1)"%I1)
print("Квадратичный интегральный  критерий качества I2 =%s (настройки №1"%I11)
print("Линейный интегральный критерий качества I1 =%s (настройки №2 )"%I2)
print("Квадратичный интегральный критерий качества I2 =%s (настройки №2)"%I21)
print("Линейный интегральный критерий качества I1 =%s (настройки №3 )"%I3)
print("Квадратичный интегральный критерий качества I2 =%s (настройки №3)его"%I31)
Rez=[I1+I11,I2+I21,I3+I31]
In=Rez.index(min(Rez))
print("Оптимальные параметры по интегральным критериям :\n %s"%d[In])
plt.figure()
plt.title("Переходные характеристики замкнутой АСР \n с ПИД регулятором")
plt.plot(tt,h1,'r',linewidth=1,label=' Для настройки №1 ПИД регулятора')
plt.plot(tt,h2,'b',linewidth=1,label=' Для настройки №2 ПИД регулятора')
plt.plot(tt,h3,'g',linewidth=1,label=' Для настройки №3 ПИД регулятора')
plt.legend(loc='best')
plt.grid(True)
plt.show()


Выводы


Разработано программное обеспечение, для реализации в полном объёме поискового метода определения оптимальных настроек ПИД регуляторов с использованием интегрального критерия, объединяющего преимущества его линейного и квадратичного представления.
Теги:
Хабы:
Всего голосов 22: ↑16 и ↓6+10
Комментарии2
72
Карма
0
Рейтинг
Юрий Тараненко @Scorobey

Разработчик учебных программ

Отправить сообщение

Публикации

Истории

Работа

Python разработчик
110 вакансий
Программист Delphi
3 вакансии
Django разработчик
28 вакансий
Системный аналитик
464 вакансии
Data Scientist
70 вакансий

Ближайшие события

8 октября – 4 декабря
ТурбоХакатон «Решения для электроэнергетики на базе искусственного интеллекта»
Онлайн
Больше событий в календаре
Разработка
Другое
20 ноября
Конференция InterComm «Рождение Титанов»
Москва
Больше событий в календаре
Менеджмент
Другое
22 – 24 ноября
Хакатон «AgroCode Hack Genetics'24»
Онлайн
Больше событий в календаре
Разработка
Другое
23 ноября
Офлайн-конференция «Soft Weekend»
Москва
Больше событий в календаре
Разработка
Менеджмент
Другое
28 ноября
Конференция «TechRec: ITHR CAMPUS»
Москва • Онлайн
Больше событий в календаре
Менеджмент
Другое
25 – 26 апреля
IT-конференция Merge Tatarstan 2025
Казань
Больше событий в календаре
Разработка
Маркетинг
Другое

Ваш аккаунт

Разделы

Информация

Услуги

Техническая поддержка
© 2006–2024, Habr