Человеческий мозг по своей природе очень плохо умеет оценивать вероятность срабатывания случайных событий, на основании выданной числовой оценки. И довольно хорошо на основании качественных оценок. А все потому, что человек мысленно делает конвертацию числовых вероятностей в качественные оценки, и делает это очень субъективно:
В статье будут рассмотрены следующие вопросы:
В процессе эволюции человеческий мозг учился очень хорошо оперировать качественными оценками событий и образами своего опыта. А числа и абстрактную числовую оценку вероятности «случайных» событий человек придумал сравнительно недавно [1]. Тем не менее эти числа человек в своих оценках всё равно преобразует в качественные представления: чуть-чуть, мало, много, опасно, безопасно, достаточно. Оценки эти всегда зависят от контекста и субъективного отношения к этому контексту. Именно это и является основной причиной ошибочных числовых допущений.
В качестве примера будет рассмотрена пошаговая игра Disciples 2 [2]. В данной части статьи не будет рассматриваться качество генерации случайных чисел конкретно в этой игре. Про их генерацию будет достаточно данных во второй части статьи.
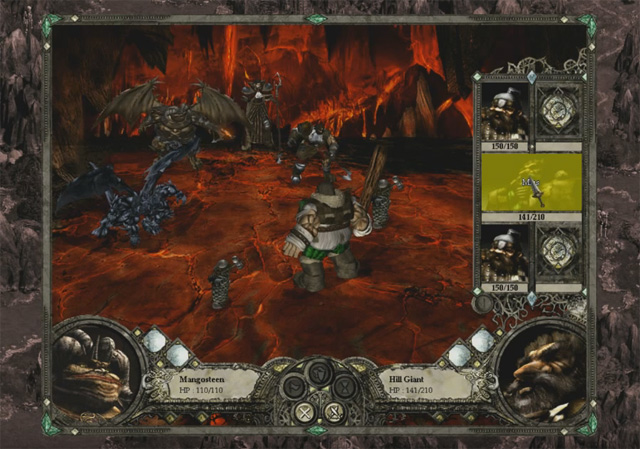 Disciples 2 — типичный промах [2]
Disciples 2 — типичный промах [2]
Стандартная атака ближнего боя имеет шанс попадания 80%. Обычно этот шанс воспринимается игроком как "почти всегда", а риск промаха — "изредка / время от времени". Вероятность промахнуться 2 раза подряд при двух атаках равна 4%. Игрок этот риск воспринимает как "почти никогда / такое будет случаться крайне редко". И когда подобное случается, игроки возмущаются на «кривой рандом»: [3]; [4].
Но в ситуациях с двумя промахами подряд и оценкой риска в 4% беглая оценка игроком имеет несколько ошибочных допущений:
1. 4% это вовсе не "почти никогда". Это событие, которое будет случаться в каждом 25-ом независимом эксперименте (в среднем).
2. Оценка проводится на неправильном отрезке времени. Минимальным отрезком замера атак по 80% следует брать не 2 атаки, а все атаки одного класса (~80%) за время «настороженной» памяти игрока. Чаще всего за это время можно взять долгую игровую сессию или вообще всю игру, тут всё зависит от типа игры, памяти игрока и предпочтений считающего.
Так как настоящей статистики использования этой игры у меня нет, я буду исходить из предположения, что долгая игровая сессия в Disciples 2 длится 3 часа и за это время совершается около 250 атак с меткостью ~80%. Стоит заметить, что промахи врагов следует игнорировать, т.к. их промахи игрока не злят, и он редко их запоминает.
Так вот, оценивать следует ситуацию: «За все 250 атак ни разу не произойдет 2 промахов подряд».
Для подсчета вероятности истинности данного события была использована рекуррентная формула: P1(n)=0.8*P1(n-1)+0.16*P1(n-2). В выведении этой формулы я воспользовался помощью сообщества, цитата вычислений, подробности и результат приведены ниже.
Для решения задачи вместо того, чтобы разбираться с методами решения рекуррентных соотношений, был написан маленький javascript код для консоли браузера и вычислен результат.
В итоге ответ: 0.0001666846271670716
Или 0.0167%
Этот ответ совпадает с ответом другого автора Kojiec9: 0.000166684627177505 [6], который использовал свой выработанный метод с пятиричной системой счисления и вычислил результат по своей формуле в Паскале. Незначительные различия в ответах, объясняются, судя по всему, округлениями float чисел.
Так вот, за 3 часа игры в Disciples 2 игрок имеет шанс избежать двойного промаха при 80% меткости всего в 0.0167%. Вот это уже действительно очень маловероятно. (а вероятность хотя бы одного двойного промаха, соответственно равна 99.9833%).
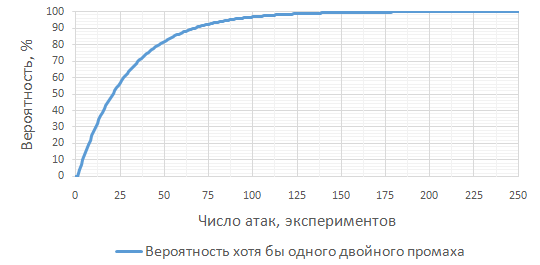 Рост вероятности хотя бы одного двойного промаха с ростом числа экспериментов
Рост вероятности хотя бы одного двойного промаха с ростом числа экспериментов
Про несовершенство и искажения человеческой памяти, кстати, вообще целые исследования и книги существуют: «Иллюзии мозга. Когнитивные искажения из-за переизбытка информации» [7]; «Не верьте своему мозгу» [8], если вас эта тема заинтересовала, рекомендую начать ознакомление с этих статей.
3. Третье неверное допущение — это ожидание зависимости во взаимно независимых экспериментах.
То есть после первого промаха игрок думает:
«Так, персонаж промахнулся с меткостью 80%. Теперь-то он точно попадёт, ведь риск двойного промаха равен всего 4%».
А вот и нет. После первого промаха риск очередного промаха будет так же равен 20%. Ведь прошлая атака уже случилась и никак не влияет на будущий выстрел. Более того, если до первой атаки вероятность двойного промаха была равна 4%, то после первого промаха вероятность двойного промаха становится уже 20%, то есть относительно ожиданий игрока риск только возрастает.
Эта особенность человеческого мозга особенно привлекательна для манипуляций со стороны казино (и им подобных) в азартных играх (подробнее об устройстве игровых автоматов от производителя [9]).
Ещё интересные примеры заблуждений человеческого мозга можно почерпнуть в статьях про баланс Яна Шрайбера «Level 5: Probability and Randomness Gone Horribly Wrong» (Уровень 5. Вероятность и случайность пошли вразнос) [10].
Используемый в играх термин «Генератор случайных чисел» (RNG / random number generator) почти всегда в действительности означает «Генератор псевдослучайных чисел» [11]. Главной особенностью этого генератора является его воспроизводимость. Воспроизводимость означает то, что, зная изначальный порождающий элемент (или зерно / seed) всегда будет получена одна и та же последовательность случайных (псевдослучайных) чисел. В некоторых играх этот эффект проявляется в том, что после перезагрузки игры последовательность попаданий и промахов остается неизменной. А в других играх не остается той же самой.
А все дело в том, как применяется этот генератор псевдослучайных чисел и какие дизайнерские цели преследует разработчик.
Чтобы лучше понять принцип работы генератора псевдослучайных чисел, можно рассмотреть способ его реализации в первых классических играх, когда ресурсы компьютеров (и консолей) были особенно сильно ограниченны. (Углубленное описание примеров и их особенностей читайте в статье «How classic games make smart use of random number generation» [12].)
 How classic games make smart use of random number generation [12]
How classic games make smart use of random number generation [12]
В Final Fantasy I использовались несколько таблиц с заранее заданными фиксированными числами с 256 значениями в каждой таблице:
В качестве зерна (порождающего элемента) в Final Fantasy I используется порядковый номер (индекс) фиксированного значения в таблице. То есть, зная место, откуда будут дальше выбираться случайные числа, можно точно предсказать какое случайное число будет выдано после 1000 проверок. В более сложных алгоритмах генерации псевдослучайных чисел зерно используется не так просто, но основной принцип и эффект остаются.
Сейчас для генерации псевдослучайных чисел в основном используются стандартные библиотеки используемых языков программирования. В качестве источника энтропии чаще всего используется текущее системное время. Для нужд игровой индустрии характеристик стандартных библиотек обычно хватает. Недостатки генератора и источника энтропии используются игроками очень редко из-за сложности их вычисления и манипулирования. Обычно это остаётся уделом спидранеров-программистов (например, взламывающего логику Pokemon Colosseum [13]), а значит разработчикам такие тонкости чаще всего разумнее игнорировать.
1. Зерно фиксируется на момент старта миссии или игровой кампании.
Последствия для игрока: перезагрузка игры не изменит факт промаха персонажем (назовем его чокнутым Фиделем), даже если вероятность его попадания равна 99%. Однако, перед попыткой попасть игрок может совершить какое-либо другое действие, которое использует случайное число, например, походит другим персонажем — лысым Миком. В результате этого несчастливое случайное число будет использовано лысым Миком, а на чокнутого Фиделя будет использовано следующее случайное число в последовательности — тогда он, возможно, попадёт.
Как игрок может злоупотребить этим: если бросок с меткостью 50% приводит к промаху, то можно перезагрузиться и попробовать атаку с меткостью чуть-чуть повыше (55%), пока не попадёт. После попадания сохраниться и повторить это с другими бросками.
Положительные последствия для разработчика:
1) Игру можно воспроизвести пошагово, если хранить только начальное состояние, зерно и последовательность действий. Благодаря этому можно показывать повторы и даже очень компактно хранить файлы сохранений. Способ позволяет очень сильно сэкономить занимаемое место на диске/памяти.
2) Защита внутренних азартных игр, чтобы сохранение/загрузка не позволяла игроку обанкротить всех встречающихся NPC соперников.
Пример:
Игра roguelike Brogue [14] использует этот способ, начиная с генерации игрового мира и заканчивая просчетом всех действий игрока. В результате этого в файле сохранения хранится только стартовое зерно и последовательность игровых команд. Дополнительный бонус этого эффекта в том, что игру можно начать с выбранным номером зерна, предварительно выбрав наиболее интересный мир в таблицах сгенерированных миров Brogue [15].
 Brogue roguelike — официальный сайт [14]
Brogue roguelike — официальный сайт [14]
2. Зерно не фиксируется или обновляется каждый раз после перезагрузки.
Последствия для игрока: любая перезагрузка изменяет все расчеты в шансах попаданий.
Как игрок может злоупотребить этим: очень просто — несколько перезагрузок и самый маловероятный сценарий попадания может стать реальностью.
Положительные последствия для разработчика:
1) Игроки воспринимают такую игру как более честную с настоящей случайностью, просто из-за отсутствия знаний внутренних механик.
2) Игроки получают неофициальный лёгкий режим, который при желании позволяет сильно облегчить сложные участки.
3) Разработчик может прикрыть халяву разными методами: одним автосохранением на игру (то есть перезаписывание сохранений и перманентная смерть) или запретом сохранения во время миссии (в разных вариациях). А наиболее чувствительные участки (азартные мини игры) можно просчитывать на основании отдельного неизменного зерна, хотя технически это значительно труднее.
Пример:
Игра The Battle for Wesnoth [16] использует нефиксированное зерно с принципиально честной случайностью. Честность заключается в том, что иногда возможны совершенно маловероятные последовательности неудач, и движок игры их не корректирует. Результатом этого являются периодические гневные посты раздраженных игроков в адрес разработчиков игры.
 Reddit — супер ловкая русалка в Wesnoth [17]
Reddit — супер ловкая русалка в Wesnoth [17]
Также перед атакой игра предоставляет подробные расчеты вероятностей каждого из возможных исходов атаки: наносимый урон, получаемый урон и вероятность гибели одного из противников. Вывод этих вероятностей только накаляет гнев «неудачно походивших», т.к. уверившись в хороших шансах при атаке, сложно смириться с результатом, у которого была оценка 1 к 1000.
3. Зерно не фиксируется, а сами результаты подвергаются дополнительным манипуляциям.
Под манипуляциями я имею в виду такие динамические корректировки, в результате которых увеличивается ощущение правильной (справедливой) случайности за счёт потери настоящей псевдослучайности в получаемых числах.
Последствия для игрока: аналогично играм с нефиксированным зерном — перезагрузка позволяет пересчитать результаты.
Как игрок может злоупотребить этим: с помощью сейвскаминга можно подобрать выгодную комбинацию атак, но во многом зависит от способа реализации и наличия защитных механизмов со стороны разработчика.
Положительные последствия для разработчика: разработчик может контролировать редкость нежелательных исходов, делать видимость "честного рандома", увеличивать и уменьшать сложность игры. Если разработчик при подсчете шанса на попадания хранит и раздельно учитывает срабатывания для каждой команды, то он может сильно уменьшить злоупотребления от сейвскаминга, гарантируя, что свою среднеарифметическую порцию урона игрок всё равно получит.
Примеры:
Разработчик Carsten Germer использует функцию контролируемой случайности для редких и не только событий [18]. Например, чтобы гарантировать периодическое выпадение особо редкого бонуса с шансом 1 к 10000, он после каждого «промаха» увеличивает шансы по порядку: 1 к 9900; 1 к 9800; 1 к 9700… и так до фиксации события. А чтобы гарантировать отсутствие частых редкостей, он ввел дополнительную переменную, блокирующую срабатывание на 100% в течение 10 следующих проверок после прошлого срабатывания.
В своем рогалике Grue the Monster [19] я также использовал манипуляции со случайностями. Обычно при преследовании жертв персонаж игрока должен прятаться за их спинами, поджидая, когда они сделают шаг назад и попадут к нему в лапы. Обычно такой шанс равен 1/6 в открытом пространстве (1/2 в коридорах и 1/1 в тупиках), но чтобы уменьшить раздражающий эффект особенно невезучих ситуаций, перед каждой проверкой направления хода жертвы в 15% случаев она гарантированно шла в направлении к Гру.
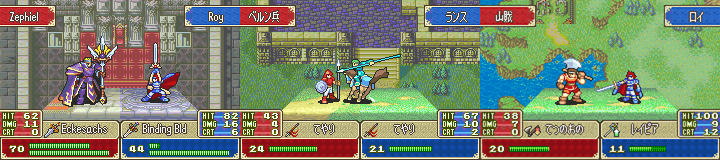
Самый интересный случай: в игре Fire Emblem: The Binding Blade [20] была реализована скрытая механика определения попадания при атаках [21]. Традиционно для серии вероятность попадания показывается игрой в процентах от 0 до 100%. В более ранних играх серии факт попадания определялся одним случайным числом от 1 до 100: если выпадающее число (например, 61) меньше или равно вероятности попадания (например, 75), то засчитывается удар, если больше, то промах.
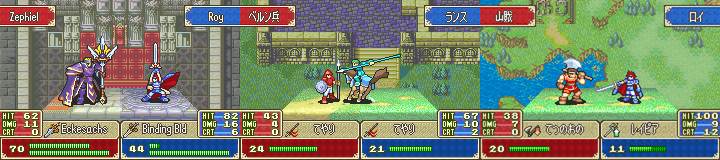 Fire Emblem: The Binding Blade [20]
Fire Emblem: The Binding Blade [20]
В данной части была введена щадящая система: вместо одного случайного числа бралось среднее двух случайных чисел, и это среднее сравнивалось со значением меткости. То есть случайное число в большей степени стремится к значению 50. Это приводит к искажению линейного эффекта случайности попадания: бойцы с меткостью больше 50% попадают чаще, чем в 50% случаев, а с меткостью меньше 50% значительно реже. А так как в игре подавляющее большинство персонажей игрока имеют большую меткость, а большинство врагов меньшую, то игрок получает очень серьёзное скрытое преимущество [21]. Ниже показан график этого эффекта, где синей линий показана частота попаданий в старой системе, а красной частота попаданий в новой в зависимости процента меткости атакующего. Например, при показываемой вероятности попадания в 90%, фактическая вероятность будет равна 98,1%, при 80% — 92,2%, а при 10% — всего 1,9%!
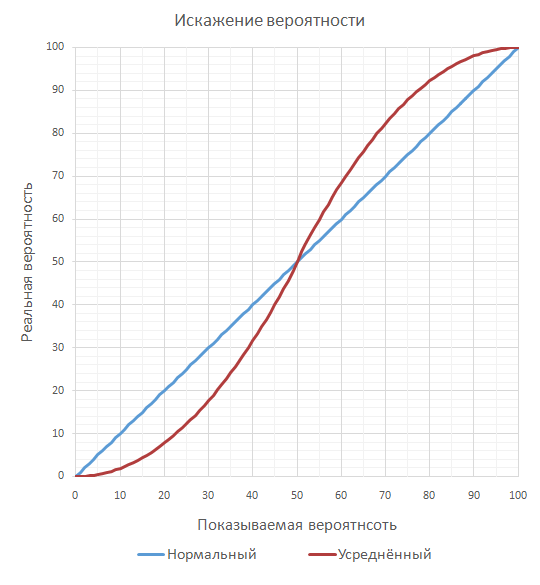 Искажение шанса попадания. По оси Y фактическая вероятность, по оси X — показываемая игроку
Искажение шанса попадания. По оси Y фактическая вероятность, по оси X — показываемая игроку
Это, безусловно, не единственные примеры манипуляций со случайными числами и балансом, но найти их очень сложно. Поэтому помощь сообщества здесь будет особенно ценной.
Хочу отметить, что я не отношу к манипулируемой случайности процедурную генерацию, как таковую. Пример: рогалик сгенерировал случайный уровень со случайным набором врагов, ловушек, стен и тупиков. Если при этом был создан уровень, который невозможно пройти, то пример кривой разработки, недостаточно продуманного проектирования или слабого тестирования. Разработчик обязан процедурно проверять хотя бы базовые проблемы случайной генерации:
Такое вмешательство в случайные результаты не являются манипуляцией, а являются просто правилом минимально грамотного подхода к разработке. Используются эти проверки во всех способах генерации псевдослучайных чисел.
4. Вообще убрать элемент случайности из механики игры.
То есть результаты каждой атаки всегда имеют 100% вероятность попадания и фиксированный урон, а также постоянные правила срабатывания дополнительных эффектов. Вместо этого можно использовать случайные вычисления для косметических целей: периодические «позёвывания» ожидающих своего хода персонажей; отлетание чисел нанесенного урона; эффекты столкновений и взрывов. Тут нет никакой разницы, как генерировать случайные числа и насколько равномерно распределение.
Хотя и в этом случае можно использовать первые три способа в расчетах искусственного интеллекта, когда вражеские персонажи могут в какой-либо степени случайно выбирать цели для атаки или ходить командой в случайном порядке. Но это уже будет менее заметно для игрока и раздражающих ситуаций будет значительно меньше.
Последствия для игрока: перезагрузка либо никак не влияет на результаты, либо влияет незначительно.
Как игрок может злоупотребить этим: игрок может вычислить или найти в сети стабильную доминирующую стратегию и использовать только её. Стоит отметить, что для определённых групп игроков это является основным интересом в игре.
Положительные последствия для разработчика: разработчику значительно легче сбалансировать такую игру. Как минус — при этом возникающие доминирующие стратегии становятся стабильными, а значит, даже невезение игрока не сможет привести его к поражению, а приводит к исчезновению всяких неожиданностей, скуке и удалению игры. Игроки высокого класса почти всегда будут выигрывать у игроков классом пониже, для различных типов игр это может быть как преимуществом, так и недостатком.
Пример:
Любые шахматы с классическими правилами.
Также сюда подходят логические roguelike. Например, очень хорошо данный метод реализован в Desktop Dungeons Alpha [22].
 Desktop Dungeons Alpha [22]
Desktop Dungeons Alpha [22]
Здесь результаты последовательности атак всегда одинаковы и заранее просчитываемы. Однако за счет случайной (процедурной) генерации игровых подземелий и наличия тумана войны, игра приобретает свою уникальную реиграбельность лучших рогаликов.
Таким образом, в статье рассмотрены две подтемы случайности в играх:
- 80% попадания выстрела в игре — ну это почти гарантированное попадание;
- 80% того, что ваш товарищ хоть когда-нибудь отдаст долг — не-не-не, так не пойдёт, это слишком большой риск;
- 5% получения критического урона он NPC врага — маловероятно, риск можно игнорировать;
- 1% риск падения сосульки, если пройти под крышей с капающими метровыми сосульками — ещё чего, лучше обойти с другой стороны тротуара;
- 51% вероятность выигрыша в мини-игре в большой РПГ — можно рассчитывать на то, что после 20 ставок я чуть-чуть выиграю или, как минимум, останусь при своих… через 20 ставок… как такое могло случиться, что я проиграл половину всего своего золота? Тут явно сломан генератор случайных чисел!
В статье будут рассмотрены следующие вопросы:
- ошибочные допущения в оценке вероятностей;
- конкретные примеры заблуждений игроков и фактические вероятности «редких» событий;
- генератор случайных чисел (вообще-то псевдослучайных);
- ранние простые генераторы псевдослучайных чисел на примере Final Fantasy I;
- подходы к реализации случайных событий с воспроизводимостью и без;
- примеры удачно внедренных разных подходов и манипуляции в Fire Emblem.
I. Ошибочные допущения в оценке вероятностей
В процессе эволюции человеческий мозг учился очень хорошо оперировать качественными оценками событий и образами своего опыта. А числа и абстрактную числовую оценку вероятности «случайных» событий человек придумал сравнительно недавно [1]. Тем не менее эти числа человек в своих оценках всё равно преобразует в качественные представления: чуть-чуть, мало, много, опасно, безопасно, достаточно. Оценки эти всегда зависят от контекста и субъективного отношения к этому контексту. Именно это и является основной причиной ошибочных числовых допущений.
В качестве примера будет рассмотрена пошаговая игра Disciples 2 [2]. В данной части статьи не будет рассматриваться качество генерации случайных чисел конкретно в этой игре. Про их генерацию будет достаточно данных во второй части статьи.
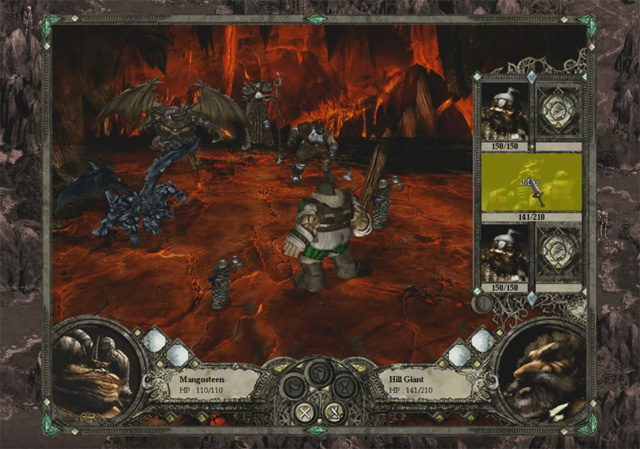
Стандартная атака ближнего боя имеет шанс попадания 80%. Обычно этот шанс воспринимается игроком как "почти всегда", а риск промаха — "изредка / время от времени". Вероятность промахнуться 2 раза подряд при двух атаках равна 4%. Игрок этот риск воспринимает как "почти никогда / такое будет случаться крайне редко". И когда подобное случается, игроки возмущаются на «кривой рандом»: [3]; [4].
Но в ситуациях с двумя промахами подряд и оценкой риска в 4% беглая оценка игроком имеет несколько ошибочных допущений:
1. 4% это вовсе не "почти никогда". Это событие, которое будет случаться в каждом 25-ом независимом эксперименте (в среднем).
2. Оценка проводится на неправильном отрезке времени. Минимальным отрезком замера атак по 80% следует брать не 2 атаки, а все атаки одного класса (~80%) за время «настороженной» памяти игрока. Чаще всего за это время можно взять долгую игровую сессию или вообще всю игру, тут всё зависит от типа игры, памяти игрока и предпочтений считающего.
Так как настоящей статистики использования этой игры у меня нет, я буду исходить из предположения, что долгая игровая сессия в Disciples 2 длится 3 часа и за это время совершается около 250 атак с меткостью ~80%. Стоит заметить, что промахи врагов следует игнорировать, т.к. их промахи игрока не злят, и он редко их запоминает.
Так вот, оценивать следует ситуацию: «За все 250 атак ни разу не произойдет 2 промахов подряд».
Для подсчета вероятности истинности данного события была использована рекуррентная формула: P1(n)=0.8*P1(n-1)+0.16*P1(n-2). В выведении этой формулы я воспользовался помощью сообщества, цитата вычислений, подробности и результат приведены ниже.
Можно попробовать применить индукцию. Введём несколько обозначений. Вероятность сохранить лапу после n-й вылазки обозначим P(n). Представим эту вероятность в виде суммы двух вероятностейЦитата с решением задачи от пользователя Serbbit [6]
P(n) = P1(n)+P2(n), где P1(n) это вероятность, при которой крайняя n-ая вылазка оказалась удачной, а P2(n) — неудачной.
Может показаться что P1 и P2 пропорциональны 0.8 и 0.2, но это не так. Из-за того что мы рассматриваем не любые возможные исходы, а только те, которые сохранили лапу еноту.
Попробуем теперь вывести рекуррентную формулу
P1(n)=0.8*(P1(n-1)+P2(n-1))
P2(n)=0.2*P1(n-1)
Подставим P2 в формулу для P1 получим
P1(n)=0.8*P1(n-1)+0.16*P1(n-2)
Дальше Решение рекуррентных соотношений [5]
Для решения задачи вместо того, чтобы разбираться с методами решения рекуррентных соотношений, был написан маленький javascript код для консоли браузера и вычислен результат.
var P1 = [];
P1[0] = 1;
P1[1] = 1;
for (var n=2; n<=250; n++) {
P1[n] = 0.8 * P1[n-1] + 0.16 * P1[n-2];
console.log(n + ') ' + P1[n]);
}
// ответ: 250) 0.0001666846271670716
В итоге ответ: 0.0001666846271670716
Или 0.0167%
Этот ответ совпадает с ответом другого автора Kojiec9: 0.000166684627177505 [6], который использовал свой выработанный метод с пятиричной системой счисления и вычислил результат по своей формуле в Паскале. Незначительные различия в ответах, объясняются, судя по всему, округлениями float чисел.
Так вот, за 3 часа игры в Disciples 2 игрок имеет шанс избежать двойного промаха при 80% меткости всего в 0.0167%. Вот это уже действительно очень маловероятно. (а вероятность хотя бы одного двойного промаха, соответственно равна 99.9833%).

Про несовершенство и искажения человеческой памяти, кстати, вообще целые исследования и книги существуют: «Иллюзии мозга. Когнитивные искажения из-за переизбытка информации» [7]; «Не верьте своему мозгу» [8], если вас эта тема заинтересовала, рекомендую начать ознакомление с этих статей.
3. Третье неверное допущение — это ожидание зависимости во взаимно независимых экспериментах.
То есть после первого промаха игрок думает:
«Так, персонаж промахнулся с меткостью 80%. Теперь-то он точно попадёт, ведь риск двойного промаха равен всего 4%».
А вот и нет. После первого промаха риск очередного промаха будет так же равен 20%. Ведь прошлая атака уже случилась и никак не влияет на будущий выстрел. Более того, если до первой атаки вероятность двойного промаха была равна 4%, то после первого промаха вероятность двойного промаха становится уже 20%, то есть относительно ожиданий игрока риск только возрастает.
Эта особенность человеческого мозга особенно привлекательна для манипуляций со стороны казино (и им подобных) в азартных играх (подробнее об устройстве игровых автоматов от производителя [9]).
Ещё интересные примеры заблуждений человеческого мозга можно почерпнуть в статьях про баланс Яна Шрайбера «Level 5: Probability and Randomness Gone Horribly Wrong» (Уровень 5. Вероятность и случайность пошли вразнос) [10].
II. Генератор случайных чисел
Используемый в играх термин «Генератор случайных чисел» (RNG / random number generator) почти всегда в действительности означает «Генератор псевдослучайных чисел» [11]. Главной особенностью этого генератора является его воспроизводимость. Воспроизводимость означает то, что, зная изначальный порождающий элемент (или зерно / seed) всегда будет получена одна и та же последовательность случайных (псевдослучайных) чисел. В некоторых играх этот эффект проявляется в том, что после перезагрузки игры последовательность попаданий и промахов остается неизменной. А в других играх не остается той же самой.
А все дело в том, как применяется этот генератор псевдослучайных чисел и какие дизайнерские цели преследует разработчик.
Чтобы лучше понять принцип работы генератора псевдослучайных чисел, можно рассмотреть способ его реализации в первых классических играх, когда ресурсы компьютеров (и консолей) были особенно сильно ограниченны. (Углубленное описание примеров и их особенностей читайте в статье «How classic games make smart use of random number generation» [12].)

В Final Fantasy I использовались несколько таблиц с заранее заданными фиксированными числами с 256 значениями в каждой таблице:
- для вычисления случайных сражений с каждым шагом в игровой карте алгоритм перемещался по таблице, изменяя индекс на 1 за раз, таким образом постепенно прокручивая все возможные значения — от этого зависел как сам факт столкновения, так и возможная группа противников;
- для вычисления результатов сражения тоже использовалась подобная таблица из 256 фиксированных значений, но перемещение по ней происходило не только с каждым очередным использованием псевдослучайного числа, но и каждые 2 кадра. То есть каждые 2 кадра алгоритм вхолостую прокручивал таблицу с числами, тем самым уменьшая риск прогнозируемых одинаковых последовательностей. Источником энтропии тут была неопределенность, сколько времени игрок будет думать до выбора очередной команды.
В качестве зерна (порождающего элемента) в Final Fantasy I используется порядковый номер (индекс) фиксированного значения в таблице. То есть, зная место, откуда будут дальше выбираться случайные числа, можно точно предсказать какое случайное число будет выдано после 1000 проверок. В более сложных алгоритмах генерации псевдослучайных чисел зерно используется не так просто, но основной принцип и эффект остаются.
Сейчас для генерации псевдослучайных чисел в основном используются стандартные библиотеки используемых языков программирования. В качестве источника энтропии чаще всего используется текущее системное время. Для нужд игровой индустрии характеристик стандартных библиотек обычно хватает. Недостатки генератора и источника энтропии используются игроками очень редко из-за сложности их вычисления и манипулирования. Обычно это остаётся уделом спидранеров-программистов (например, взламывающего логику Pokemon Colosseum [13]), а значит разработчикам такие тонкости чаще всего разумнее игнорировать.
III. Разные подходы к использованию генератора
1. Зерно фиксируется на момент старта миссии или игровой кампании.
Последствия для игрока: перезагрузка игры не изменит факт промаха персонажем (назовем его чокнутым Фиделем), даже если вероятность его попадания равна 99%. Однако, перед попыткой попасть игрок может совершить какое-либо другое действие, которое использует случайное число, например, походит другим персонажем — лысым Миком. В результате этого несчастливое случайное число будет использовано лысым Миком, а на чокнутого Фиделя будет использовано следующее случайное число в последовательности — тогда он, возможно, попадёт.
Как игрок может злоупотребить этим: если бросок с меткостью 50% приводит к промаху, то можно перезагрузиться и попробовать атаку с меткостью чуть-чуть повыше (55%), пока не попадёт. После попадания сохраниться и повторить это с другими бросками.
Положительные последствия для разработчика:
1) Игру можно воспроизвести пошагово, если хранить только начальное состояние, зерно и последовательность действий. Благодаря этому можно показывать повторы и даже очень компактно хранить файлы сохранений. Способ позволяет очень сильно сэкономить занимаемое место на диске/памяти.
2) Защита внутренних азартных игр, чтобы сохранение/загрузка не позволяла игроку обанкротить всех встречающихся NPC соперников.
Пример:
Игра roguelike Brogue [14] использует этот способ, начиная с генерации игрового мира и заканчивая просчетом всех действий игрока. В результате этого в файле сохранения хранится только стартовое зерно и последовательность игровых команд. Дополнительный бонус этого эффекта в том, что игру можно начать с выбранным номером зерна, предварительно выбрав наиболее интересный мир в таблицах сгенерированных миров Brogue [15].

2. Зерно не фиксируется или обновляется каждый раз после перезагрузки.
Последствия для игрока: любая перезагрузка изменяет все расчеты в шансах попаданий.
Как игрок может злоупотребить этим: очень просто — несколько перезагрузок и самый маловероятный сценарий попадания может стать реальностью.
Положительные последствия для разработчика:
1) Игроки воспринимают такую игру как более честную с настоящей случайностью, просто из-за отсутствия знаний внутренних механик.
2) Игроки получают неофициальный лёгкий режим, который при желании позволяет сильно облегчить сложные участки.
3) Разработчик может прикрыть халяву разными методами: одним автосохранением на игру (то есть перезаписывание сохранений и перманентная смерть) или запретом сохранения во время миссии (в разных вариациях). А наиболее чувствительные участки (азартные мини игры) можно просчитывать на основании отдельного неизменного зерна, хотя технически это значительно труднее.
Пример:
Игра The Battle for Wesnoth [16] использует нефиксированное зерно с принципиально честной случайностью. Честность заключается в том, что иногда возможны совершенно маловероятные последовательности неудач, и движок игры их не корректирует. Результатом этого являются периодические гневные посты раздраженных игроков в адрес разработчиков игры.

Также перед атакой игра предоставляет подробные расчеты вероятностей каждого из возможных исходов атаки: наносимый урон, получаемый урон и вероятность гибели одного из противников. Вывод этих вероятностей только накаляет гнев «неудачно походивших», т.к. уверившись в хороших шансах при атаке, сложно смириться с результатом, у которого была оценка 1 к 1000.
3. Зерно не фиксируется, а сами результаты подвергаются дополнительным манипуляциям.
Под манипуляциями я имею в виду такие динамические корректировки, в результате которых увеличивается ощущение правильной (справедливой) случайности за счёт потери настоящей псевдослучайности в получаемых числах.
Последствия для игрока: аналогично играм с нефиксированным зерном — перезагрузка позволяет пересчитать результаты.
Как игрок может злоупотребить этим: с помощью сейвскаминга можно подобрать выгодную комбинацию атак, но во многом зависит от способа реализации и наличия защитных механизмов со стороны разработчика.
Положительные последствия для разработчика: разработчик может контролировать редкость нежелательных исходов, делать видимость "честного рандома", увеличивать и уменьшать сложность игры. Если разработчик при подсчете шанса на попадания хранит и раздельно учитывает срабатывания для каждой команды, то он может сильно уменьшить злоупотребления от сейвскаминга, гарантируя, что свою среднеарифметическую порцию урона игрок всё равно получит.
Примеры:
Разработчик Carsten Germer использует функцию контролируемой случайности для редких и не только событий [18]. Например, чтобы гарантировать периодическое выпадение особо редкого бонуса с шансом 1 к 10000, он после каждого «промаха» увеличивает шансы по порядку: 1 к 9900; 1 к 9800; 1 к 9700… и так до фиксации события. А чтобы гарантировать отсутствие частых редкостей, он ввел дополнительную переменную, блокирующую срабатывание на 100% в течение 10 следующих проверок после прошлого срабатывания.
В своем рогалике Grue the Monster [19] я также использовал манипуляции со случайностями. Обычно при преследовании жертв персонаж игрока должен прятаться за их спинами, поджидая, когда они сделают шаг назад и попадут к нему в лапы. Обычно такой шанс равен 1/6 в открытом пространстве (1/2 в коридорах и 1/1 в тупиках), но чтобы уменьшить раздражающий эффект особенно невезучих ситуаций, перед каждой проверкой направления хода жертвы в 15% случаев она гарантированно шла в направлении к Гру.
Самый интересный случай: в игре Fire Emblem: The Binding Blade [20] была реализована скрытая механика определения попадания при атаках [21]. Традиционно для серии вероятность попадания показывается игрой в процентах от 0 до 100%. В более ранних играх серии факт попадания определялся одним случайным числом от 1 до 100: если выпадающее число (например, 61) меньше или равно вероятности попадания (например, 75), то засчитывается удар, если больше, то промах.
В данной части была введена щадящая система: вместо одного случайного числа бралось среднее двух случайных чисел, и это среднее сравнивалось со значением меткости. То есть случайное число в большей степени стремится к значению 50. Это приводит к искажению линейного эффекта случайности попадания: бойцы с меткостью больше 50% попадают чаще, чем в 50% случаев, а с меткостью меньше 50% значительно реже. А так как в игре подавляющее большинство персонажей игрока имеют большую меткость, а большинство врагов меньшую, то игрок получает очень серьёзное скрытое преимущество [21]. Ниже показан график этого эффекта, где синей линий показана частота попаданий в старой системе, а красной частота попаданий в новой в зависимости процента меткости атакующего. Например, при показываемой вероятности попадания в 90%, фактическая вероятность будет равна 98,1%, при 80% — 92,2%, а при 10% — всего 1,9%!

Это, безусловно, не единственные примеры манипуляций со случайными числами и балансом, но найти их очень сложно. Поэтому помощь сообщества здесь будет особенно ценной.
Хочу отметить, что я не отношу к манипулируемой случайности процедурную генерацию, как таковую. Пример: рогалик сгенерировал случайный уровень со случайным набором врагов, ловушек, стен и тупиков. Если при этом был создан уровень, который невозможно пройти, то пример кривой разработки, недостаточно продуманного проектирования или слабого тестирования. Разработчик обязан процедурно проверять хотя бы базовые проблемы случайной генерации:
- проход к выходу всегда должен быть хотя бы в единственном числе. Тут помогают любые алгоритмы поиска пути;
- серия ловушек должна иметь возможность обхода, и если их создаётся слишком много в одном месте, то алгоритм должен вычислить их плотность и удалить лишние;
- слишком сильные враги должны предоставлять хотя бы один из доступных способов их «прохождения»: грубой силой; свитками и зельями; особыми артефактами или возможностью просто от них убежать.
Такое вмешательство в случайные результаты не являются манипуляцией, а являются просто правилом минимально грамотного подхода к разработке. Используются эти проверки во всех способах генерации псевдослучайных чисел.
4. Вообще убрать элемент случайности из механики игры.
То есть результаты каждой атаки всегда имеют 100% вероятность попадания и фиксированный урон, а также постоянные правила срабатывания дополнительных эффектов. Вместо этого можно использовать случайные вычисления для косметических целей: периодические «позёвывания» ожидающих своего хода персонажей; отлетание чисел нанесенного урона; эффекты столкновений и взрывов. Тут нет никакой разницы, как генерировать случайные числа и насколько равномерно распределение.
Хотя и в этом случае можно использовать первые три способа в расчетах искусственного интеллекта, когда вражеские персонажи могут в какой-либо степени случайно выбирать цели для атаки или ходить командой в случайном порядке. Но это уже будет менее заметно для игрока и раздражающих ситуаций будет значительно меньше.
Последствия для игрока: перезагрузка либо никак не влияет на результаты, либо влияет незначительно.
Как игрок может злоупотребить этим: игрок может вычислить или найти в сети стабильную доминирующую стратегию и использовать только её. Стоит отметить, что для определённых групп игроков это является основным интересом в игре.
Положительные последствия для разработчика: разработчику значительно легче сбалансировать такую игру. Как минус — при этом возникающие доминирующие стратегии становятся стабильными, а значит, даже невезение игрока не сможет привести его к поражению, а приводит к исчезновению всяких неожиданностей, скуке и удалению игры. Игроки высокого класса почти всегда будут выигрывать у игроков классом пониже, для различных типов игр это может быть как преимуществом, так и недостатком.
Пример:
Любые шахматы с классическими правилами.
Также сюда подходят логические roguelike. Например, очень хорошо данный метод реализован в Desktop Dungeons Alpha [22].

Здесь результаты последовательности атак всегда одинаковы и заранее просчитываемы. Однако за счет случайной (процедурной) генерации игровых подземелий и наличия тумана войны, игра приобретает свою уникальную реиграбельность лучших рогаликов.
Заключение
Таким образом, в статье рассмотрены две подтемы случайности в играх:
- Ошибочные допущения в оценке вероятностей. Описаны интуитивные допущения, которые делает игрок, и которые часто оказываются неправильными из-за их субъективности. Основной вывод: настоящая случайность не только не гарантирует того, что пользователи останутся довольны, но даже может привести к обратному эффекту.
- Генерация псевдослучайных чисел. Описаны разные подходы к использованию случайности. Удачные примеры реализации показывают, что независимо от выбранного подхода игра может получится интересной, неожиданной и с хорошей степенью реиграбельности.
Осознанное последовательное использование выбранного подхода позволяет разработчикам подчеркнуть их положительные стороны и минимизировать отрицательные.
Источники и литература
1. История математики, теория вероятностей — Википедия.
2. Disciples 2 — GOG Gold.
3. Disciples 2 — комментарий про кривой рандом №1.
4. Disciples 2 — комментарий про кривой рандом №2.
5. Решение рекуррентных соотношений.
6. Цитата с решением задачи от пользователя Serbbit.
7. Иллюзии мозга. Когнитивные искажения из-за переизбытка информации.
8. Не верьте своему мозгу.
9. Игровой аппарат изнутри и снаружи. Обзор от производителя.
10. Level 5: Probability and Randomness Gone Horribly Wrong.
11. Генератор псевдослучайных чисел — Википедия.
12. How classic games make smart use of random number generation.
13. Controlling luck in video games — Pokemon Colosseum and XD.
14. Brogue roguelike — официальный сайт.
15. The Brogue Seed Scummer.
16. The Battle for Wesnoth.
17. Супер ловкая русалка в Wesnoth.
18. «Not So Random Randomness» in Game Design and Programming.
19. Grue the Monster roguelike.
20. Fire Emblem: The Binding Blade.
21. Random Number Generator in Fire Emblem.
22. Desktop Dungeons Alpha roguelike.
2. Disciples 2 — GOG Gold.
3. Disciples 2 — комментарий про кривой рандом №1.
4. Disciples 2 — комментарий про кривой рандом №2.
5. Решение рекуррентных соотношений.
6. Цитата с решением задачи от пользователя Serbbit.
7. Иллюзии мозга. Когнитивные искажения из-за переизбытка информации.
8. Не верьте своему мозгу.
9. Игровой аппарат изнутри и снаружи. Обзор от производителя.
10. Level 5: Probability and Randomness Gone Horribly Wrong.
11. Генератор псевдослучайных чисел — Википедия.
12. How classic games make smart use of random number generation.
13. Controlling luck in video games — Pokemon Colosseum and XD.
14. Brogue roguelike — официальный сайт.
15. The Brogue Seed Scummer.
16. The Battle for Wesnoth.
17. Супер ловкая русалка в Wesnoth.
18. «Not So Random Randomness» in Game Design and Programming.
19. Grue the Monster roguelike.
20. Fire Emblem: The Binding Blade.
21. Random Number Generator in Fire Emblem.
22. Desktop Dungeons Alpha roguelike.













