Приветствую всех читателей Хабра! Меня зовут Юрий, более 20 лет преподаю высокие технологии, Oracle, Microsoft и другие, а также занимаюсь созданием, разработкой и поддержкой нагруженных информационных систем для различных бизнес-заказчиков. Сегодня хотел бы рассказать вам об актуальном направлении: собеседованиях по технологиям обработки данных.
На собеседованиях такого плана работодателю бесполезно спрашивать у соискателя о технологиях, связанных с традиционным программированием. Поэтому я популярно расскажу, как готовиться к собеседованию только в одной узкой области, связанной с языками обработки информации, а именно — обработкой длинных целых чисел (длинная арифметика) и выявления информационных свойств объектов реального мира, которые описываются в длинных целых числах.
1. Собеседование с вопросами по технологиям обработки данных обычно проводится при наборе команд аналитиков и разработчиков, ранее уже имевших опыт разработки на декларативных, императивных, объектно-ориентированных и функциональных языках.
Задача. Определите язык программирования по фрагменту программы.

Следовательно, сначала надо подготовиться к вопросу — а что уже есть хорошего в выбранном языке, что могло бы заинтересовать потенциального работодателя? Кстати, список может разниться от версии к версии, от библиотеки к библиотеке, от реализации к реализации.

Задача. На каких языках есть поддержка арифметики с длинными целыми?
2. Если работодателем заранее составлен список, то необходимо вычленить общие части языков, которые будут обсуждаться на собеседовании.
Задача. Какие, по вашему мнению, самые востребованные языки с точки зрения работодателя? Тут можно посмотреть ответ на основе статистики.
В больших и сверхбольших информационных системах чаще всего выполняется ряд вполне рутинных операций: различного вида сортировки, поиск по тем или иным критериям, алгоритмы на графах, задачи оптимизации на множествах разной природы, задачи по конструированию объектов с неопределенными свойствами. Но, из-за масштабности задачи, самые простая сортировка может выполняться месяц, а поиск — неделю. Примерная задача на понимание.
Задача. За окном стоит береза. На ней, как подсчитали ваши коллеги, 100 000 листьев, диаметр ствола у корня — 60 сантиметров. Запишите указанные параметры в любой математической нотации. И докажите ее пригодность: для переписки с коллегой, так как дерево хотят спилить. Или для компьютерной обработки его изображения.

3. Несколько слов о математической части. В жизни мы редко переходим за границы обычной арифметики. Единицы из нас используют достижения алгебры и математического анализа. Пусть указанные ниже утверждения помогут вам вспомнить, даже неглубоко, где же практически используются забытые знания.
Задача. Почему номера телефонов так долго были пяти-шестизначными? Дан ряд чисел — какое из них не является полным квадратом? Сколько автобусов в вашем городе имеют номера — полные квадраты? Сколько простых чисел до 100 вы знаете? Сколько это в процентах от всех чисел от 1 до 100? Пусть 2, 3, 5, 7 — простые числа, найдите количество простых чисел до 100. Сколько вам пришлось сделать арифметических операций? Решите эту же задачу на MS Excel для самопроверки двумя способами.
Задача. Как используется выпуклость и вогнутость на практике? Приведите 2-3 примера использования выпуклости-вогнутости.

4. Иногда необходимо пройтись по документации к системе/языку/набору библиотек, примерам из углубленных и расширенных технических описаний от самого автора/производителя. Это особенно необходимо, если подразумевается вызов нестандартных библиотек.
Задача. Запишите расширенный алгоритм Евклида на одном из указанных выше, в п.1, языков программирования. На каком языке это не нужно делать? А почему?
5. Желательно понять направление собеседования: будете ли вы писать алгоритмы самостоятельно или вам предстоит обслуживать набор сторонних алгоритмов, в котором со временем придется наводить порядок?
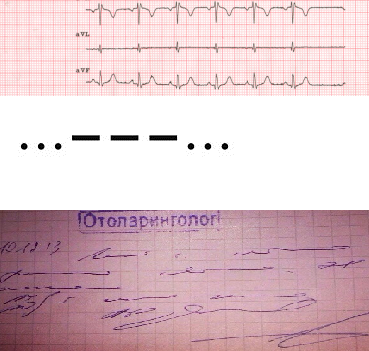
Задача. По набору записей главного врача, сделанного ручкой на блокноте стажера, необходимо компьютеризованным способом выявить, какому пациенту были сделаны назначения. Что можно посоветовать стажеру?
6. Если подразумевается выбор языка собеседования, то лучше брать более стандартизованный, чтобы у собеседующего не возникло желания менять условия задач по ходу беседы.
Задача. Сколько версий у языка Паскаль появилось за последние 25 лет? Укажите сильные и слабые стороны каждой версии.

7. Желательно сходить хотя бы на один семинар по алгоритмам и по их воплощениям в готовые информационные решения в заданной предметной области.
Задача. К вам обратился поэт с вопросом: можно ли ему написать поэму «Евгений Онегин» с учетом поэтического тезауруса данного автора. Приведите два решения этой задачи.
8. На ресурсе для программистов есть задачи для тренировки умения обрабатывать научную информацию и программировать сложные алгоритмы. Ниже мы приводим решение «в лоб», но оно не оптимальное и является лишь формулировкой условия с точки зрения языка программирования высокого уровня. Из-за недостаточно точной формулировки самого текста задачи ваши ответы могут не совпадать с ответами, которые приводят авторы этой задачи.
Пусть — наименьшее неотрицательное целое число
— наименьшее неотрицательное целое число  , для которого
, для которого  имеет наибольшее возможное значение.
имеет наибольшее возможное значение.
Например, , так как
, так как  достигает максимального значения
достигает максимального значения  при
при  и имеет меньшие значения при
и имеет меньшие значения при  . Пусть
. Пусть  для
для  ,
,  .
.
Известно, что и
и  . Найдите
. Найдите  .
.
Задача. К счастью, это очень редко решаемая на «Проекте Эйлер» задача. По заданному тексту программы найдите сильные и слабые места алгоритма и укажите их. Сможет ли эта программа решить данную задачу за рабочий день? Как ее можно ускорить? Укажите ошибки в задаче, если они есть. Найдите параметр «оченьбольшоечисло». Чем он ограничен?
9. Желаю вам пройти собеседование на хорошем уровне!
UPD Перед публикацией английской версии статьи, приводим несколько нетривиальных
соотношений, найденных после глубокой модернизации приведенного выше решения. При расчетах до .
.
 ;
;  ;
;  ;
;  .
.
На собеседованиях такого плана работодателю бесполезно спрашивать у соискателя о технологиях, связанных с традиционным программированием. Поэтому я популярно расскажу, как готовиться к собеседованию только в одной узкой области, связанной с языками обработки информации, а именно — обработкой длинных целых чисел (длинная арифметика) и выявления информационных свойств объектов реального мира, которые описываются в длинных целых числах.
1. Собеседование с вопросами по технологиям обработки данных обычно проводится при наборе команд аналитиков и разработчиков, ранее уже имевших опыт разработки на декларативных, императивных, объектно-ориентированных и функциональных языках.
Задача. Определите язык программирования по фрагменту программы.

Следовательно, сначала надо подготовиться к вопросу — а что уже есть хорошего в выбранном языке, что могло бы заинтересовать потенциального работодателя? Кстати, список может разниться от версии к версии, от библиотеки к библиотеке, от реализации к реализации.

Задача. На каких языках есть поддержка арифметики с длинными целыми?
Подумали? Примерный перечень:
- C, C++ — библиотека libgmp
- Common Lisp — не ограничивает разрядность целых чисел
- Erlang — встроенный численный тип (integer())
- Go — типы Int и Rat из библиотеки big.
- Haskell — встроенный тип Integer
- Java — класс java.math.BigInteger (февраль 1997 года)
- OCaml — библиотека num
- Pascal/Delphi — библиотека MPArith
- Perl — модули bignum и bigrat
- PHP — модуль BCMath
- Python — встроенный тип long (с момента создания языка, февраль 1991 года)
- Ruby — тип Bignum
- Scala — класс BigInt
- Scheme — с R6RS
- Языки .NET — класс System.Numerics.BigInteger (появился в .NET Framework 4.0, почти 10 лет назад)
2. Если работодателем заранее составлен список, то необходимо вычленить общие части языков, которые будут обсуждаться на собеседовании.
Задача. Какие, по вашему мнению, самые востребованные языки с точки зрения работодателя? Тут можно посмотреть ответ на основе статистики.
В больших и сверхбольших информационных системах чаще всего выполняется ряд вполне рутинных операций: различного вида сортировки, поиск по тем или иным критериям, алгоритмы на графах, задачи оптимизации на множествах разной природы, задачи по конструированию объектов с неопределенными свойствами. Но, из-за масштабности задачи, самые простая сортировка может выполняться месяц, а поиск — неделю. Примерная задача на понимание.
Задача. За окном стоит береза. На ней, как подсчитали ваши коллеги, 100 000 листьев, диаметр ствола у корня — 60 сантиметров. Запишите указанные параметры в любой математической нотации. И докажите ее пригодность: для переписки с коллегой, так как дерево хотят спилить. Или для компьютерной обработки его изображения.

3. Несколько слов о математической части. В жизни мы редко переходим за границы обычной арифметики. Единицы из нас используют достижения алгебры и математического анализа. Пусть указанные ниже утверждения помогут вам вспомнить, даже неглубоко, где же практически используются забытые знания.
Задача. Почему номера телефонов так долго были пяти-шестизначными? Дан ряд чисел — какое из них не является полным квадратом? Сколько автобусов в вашем городе имеют номера — полные квадраты? Сколько простых чисел до 100 вы знаете? Сколько это в процентах от всех чисел от 1 до 100? Пусть 2, 3, 5, 7 — простые числа, найдите количество простых чисел до 100. Сколько вам пришлось сделать арифметических операций? Решите эту же задачу на MS Excel для самопроверки двумя способами.
Задача. Как используется выпуклость и вогнутость на практике? Приведите 2-3 примера использования выпуклости-вогнутости.

4. Иногда необходимо пройтись по документации к системе/языку/набору библиотек, примерам из углубленных и расширенных технических описаний от самого автора/производителя. Это особенно необходимо, если подразумевается вызов нестандартных библиотек.
Задача. Запишите расширенный алгоритм Евклида на одном из указанных выше, в п.1, языков программирования. На каком языке это не нужно делать? А почему?
5. Желательно понять направление собеседования: будете ли вы писать алгоритмы самостоятельно или вам предстоит обслуживать набор сторонних алгоритмов, в котором со временем придется наводить порядок?
Задача. По набору записей главного врача, сделанного ручкой на блокноте стажера, необходимо компьютеризованным способом выявить, какому пациенту были сделаны назначения. Что можно посоветовать стажеру?

6. Если подразумевается выбор языка собеседования, то лучше брать более стандартизованный, чтобы у собеседующего не возникло желания менять условия задач по ходу беседы.
Задача. Сколько версий у языка Паскаль появилось за последние 25 лет? Укажите сильные и слабые стороны каждой версии.

7. Желательно сходить хотя бы на один семинар по алгоритмам и по их воплощениям в готовые информационные решения в заданной предметной области.
Задача. К вам обратился поэт с вопросом: можно ли ему написать поэму «Евгений Онегин» с учетом поэтического тезауруса данного автора. Приведите два решения этой задачи.
8. На ресурсе для программистов есть задачи для тренировки умения обрабатывать научную информацию и программировать сложные алгоритмы. Ниже мы приводим решение «в лоб», но оно не оптимальное и является лишь формулировкой условия с точки зрения языка программирования высокого уровня. Из-за недостаточно точной формулировки самого текста задачи ваши ответы могут не совпадать с ответами, которые приводят авторы этой задачи.
Задача 489 из «Проекта Эйлер»
Пусть
Например,
Известно, что
Задача. К счастью, это очень редко решаемая на «Проекте Эйлер» задача. По заданному тексту программы найдите сильные и слабые места алгоритма и укажите их. Сможет ли эта программа решить данную задачу за рабочий день? Как ее можно ускорить? Укажите ошибки в задаче, если они есть. Найдите параметр «оченьбольшоечисло». Чем он ограничен?
Еще несколько слов, если вы не смогли ее решить
Если речь шла о локальных максимумах, то ответы должны быть меньше, но после расчетов вдруг выясняется, что речь идет о глобальных максимумах, о чем в тексте задачи нет ни слова.
И еще, есть подозрение, что при любом
при любом  . Какое
. Какое  устроит авторов задачи?
устроит авторов задачи?
И еще, есть подозрение, что
Код для примерного решения
public class Start {
static BigInteger[] GcdExtended(BigInteger a, BigInteger b)
{
BigInteger res[] = new BigInteger[3];
if (b == BigInteger.valueOf(0))
{
res[0] = a; res[1] = BigInteger.valueOf(1); res[2] = BigInteger.valueOf(0);
return res;
}
res = GcdExtended(b,a.divideAndRemainder(b)[1]);
BigInteger s = res[2];
res[2] = res[1].subtract((a.divideAndRemainder(b)[0]).multiply(res[2]));
res[1] = s;
return res;
}
public static void main(String[]args) throws IOException {
BigInteger i;
BigInteger j;
int n,n1;
BigInteger temp;
BigInteger temp1;
BigInteger count;
FileWriter fileWriter = new FileWriter("c:/temp/terribleanswer.txt");
n1=1;
count=BigInteger.ZERO;
i=BigInteger.ZERO;
j=BigInteger.ZERO;
temp1=BigInteger.ZERO;
temp=BigInteger.ZERO;
for (int a=1;a<19;a++) {
for (int b=1;b<1901;b++) {
for(n=1;n<оченьбольшоечисло;n++) {
j=((BigInteger.valueOf(n)).pow(3));
j=j.add(BigInteger.valueOf(b));
i=(((BigInteger.valueOf(n)).add(BigInteger.valueOf(a))).pow(3));
i=i.add(BigInteger.valueOf(b));
int comparevalue = j.compareTo(i);
if (comparevalue==0)
{ temp=GcdExtended(i,j);
}
else if (comparevalue == 1)
{ temp=GcdExtended(j,i);
}
else { temp=GcdExtended(i,j);
}
int compareTemp = temp.compareTo(temp1);
if (compareTemp == 1) {
temp1=temp;
n1=n;
continue;
}
}
String fileContent = a + ";" + b +";"+ temp1 +";"+ n1 + "\n";
temp1=BigInteger.ZERO;
count=count.add(BigInteger.valueOf(n1));
n1=1;
try {
fileWriter.append(fileContent);
} catch (IOException e) {
}
}
}
String fileContent = count + "\n";
try {
fileWriter.append(fileContent);
} catch (IOException e) {
}
fileWriter.close();
}
}
9. Желаю вам пройти собеседование на хорошем уровне!
UPD Перед публикацией английской версии статьи, приводим несколько нетривиальных
соотношений, найденных после глубокой модернизации приведенного выше решения. При расчетах до