Содержание
- Глава 1: использование нейросетей для распознавания рукописных цифр
- Глава 2: как работает алгоритм обратного распространения
- Глава 3:
- Глава 4: визуальное доказательство того, что нейросети способны вычислить любую функцию
- Глава 5: почему глубокие нейросети так сложно обучать?
- Глава 6:
- Послесловие: существует ли простой алгоритм для создания интеллекта?
До сих пор я не объяснял, как я выбираю значения гиперпараметров – скорость обучения η, параметр регуляризации λ, и так далее. Я просто выдавал неплохо работающие значения. На практике же, когда вы используете нейросеть для атаки на проблему, может быть сложно найти хорошие гиперпараметры. Представьте, к примеру, что нам только что рассказали о задаче MNIST, и мы начали работать над ней, ничего не зная по поводу величин подходящих гиперпараметров. Допустим, что нам случайно повезло, и в первых экспериментах мы выбрали многие гиперпараметры так, как уже делали в этой главе: 30 скрытых нейронов, размер мини-пакета 10, обучение за 30 эпох и использование перекрёстной энтропии. Однако мы выбрали скорость обучения η=10,0, и параметр регуляризации λ=1000,0. И вот, что я увидел при таком прогоне:
>>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() >>> import network2 >>> net = network2.Network([784, 30, 10]) >>> net.SGD(training_data, 30, 10, 10.0, lmbda = 1000.0, ... evaluation_data=validation_data, monitor_evaluation_accuracy=True) Epoch 0 training complete Accuracy on evaluation data: 1030 / 10000 Epoch 1 training complete Accuracy on evaluation data: 990 / 10000 Epoch 2 training complete Accuracy on evaluation data: 1009 / 10000 ... Epoch 27 training complete Accuracy on evaluation data: 1009 / 10000 Epoch 28 training complete Accuracy on evaluation data: 983 / 10000 Epoch 29 training complete Accuracy on evaluation data: 967 / 10000
Наша классификация работает не лучше случайной выборки! Наша сеть работает как генератор случайного шума!
«Ну, это легко поправить, — могли бы сказать вы, — просто уменьшите такие гиперпараметры, как скорость обучения и регуляризацию». К сожалению, априори у вас нет информации по поводу того, что именно эти гиперпараметры вам нужно подстроить. Может быть, главная проблема в том, что наши 30 скрытых нейронов никогда не будут работать, вне зависимости от того, как выбираются остальные гиперпараметры? Может, нам надо не меньше 100 скрытых нейронов? Или 300? Или множество скрытых слоёв? Или другой подход к кодированию выхода? Может, наша сеть учится, но надо обучать её больше эпох? Может, размер мини-пакетов слишком мал? Может, у нас получилось бы лучше, вернись мы к квадратичной функции стоимости? Может, нам надо попробовать другой подход к инициализации весов? И так далее, и тому подобное. В пространстве гиперпараметров легко потеряться. И это может доставить реально много неудобств, если ваша сеть очень большая, или использует огромные объёмы обучающих данных, и вы можете обучать её часы, дни или недели, не получая результатов. В такой ситуации ваша уверенность начинает сдавать. Может, нейросети были неправильным подходом для решения вашей задачи? Может, вам уволиться и заняться пчеловодством?
В данном разделе я объясню некоторые эвристические подходы, которые можно использовать для настройки гиперпараметров в нейросети. Цель – помочь вам выработать рабочий процесс, позволяющий вам достаточно хорошо настраивать гиперпараметры. Конечно, я не смогу покрыть всю тему оптимизации гиперпараметров. Это огромная область, и эта не та задача, которую можно решить полностью, или по правильным стратегиям решения которой имеется всеобщее согласие. Всегда есть возможность попробовать ещё какой-нибудь трюк, чтобы выжать дополнительные результаты из вашей нейросети. Но эвристика в данном разделе должна дать вам отправную точку.
Общая стратегия
При использовании нейросети для атаки новой проблемы, первая сложность – получить от сети нетривиальные результаты, то есть, превышающие случайную вероятность. Это может оказаться удивительно сложным делом, особенно когда вы сталкиваетесь с новым классом задач. Давайте посмотрим на некоторые стратегии, которые можно использовать при подобном затруднении.
Допустим, к примеру, что вы впервые атакуете задачу MNIST. Вы начинаете с большим энтузиазмом, но полная неудача вашей первой сети вас немного обескураживает, как это описано в примере выше. Тогда нужно разобрать проблему по частям. Нужно избавиться от всех обучающих и подтверждающих изображений, кроме изображений нулей и единиц. Потом попытаться обучить сеть отличать 0 от 1. Эта задача не только по существу проще, чем различение всех десяти цифр, она также уменьшает количество обучающих данных на 80%, ускоряя обучение в 5 раз. Это позволяет гораздо быстрее проводить эксперименты, и даёт вам возможность быстрее понять, как создать хорошую сеть.
Можно ещё сильнее ускорить эксперименты, низведя сеть до минимального размера, который с большой вероятностью сможет осмысленно обучаться. Если вы считаете, что сеть [784, 10] с большой вероятностью сможет классифицировать цифры MNIST лучше, чем случайная выборка, то начинайте эксперименты с неё. Это будет гораздо быстрее, чем обучать [784, 30, 10], а до неё уже можно дорасти потом.
Ещё одно ускорение экспериментов можно получить, увеличив частоту отслеживания. В программе network2.py мы отслеживаем качество работы в конце каждой эпохи. Обрабатывая по 50 000 изображений за эпоху, нам приходится ждать довольно долго – примерно по 10 секунд на эпоху на моём ноутбуке при обучении сети [784, 30, 10] – перед тем, как получить обратную связь о качестве обучения сети. Конечно, десять секунд – это не так уж и долго, но если вы хотите попробовать несколько десятков разных гиперпараметров, это начинает раздражать, а если вы хотите попробовать сотни или тысячи вариантов, это уже просто опустошает. Обратную связь можно получать гораздо быстрее, отслеживая точность подтверждения чаще, например, каждые 1000 обучающих изображений. Кроме того, вместо использования полного набора из 10 000 подтверждающих изображений, мы можем получить оценку гораздо быстрее, используя всего 100 подтверждающих изображений. Главное, чтобы сеть увидела достаточно изображений, чтобы реально обучаться, и чтобы получить достаточно хорошую оценку эффективности. Конечно, наша network2.py пока не обеспечивает такого отслеживания. Но в качестве костылей для достижения такого эффекта в целях иллюстрации, мы обрежем наши обучающие данные до первых 1000 изображений MNIST. Попробуем посмотреть, что происходит (для простоты кода я не использовал идею того, чтобы оставить только изображения 0 и 1 – это тоже можно реализовать, приложив чуть больше усилий).
>>> net = network2.Network([784, 10]) >>> net.SGD(training_data[:1000], 30, 10, 10.0, lmbda = 1000.0, \ ... evaluation_data=validation_data[:100], \ ... monitor_evaluation_accuracy=True) Epoch 0 training complete Accuracy on evaluation data: 10 / 100 Epoch 1 training complete Accuracy on evaluation data: 10 / 100 Epoch 2 training complete Accuracy on evaluation data: 10 / 100 ...
Всё ещё получаем чистый шум, но у нас есть большое преимущество: обратная связь обновляется за доли секунды, а не каждые десять секунд. Это значит, вы можете гораздо быстрее экспериментировать с выбором гиперпараметров, или даже проводить эксперименты со множеством разных гиперпараметров почти одновременно.
В примере выше я оставил значение λ равным 1000,0, как и раньше. Но поскольку мы изменили количество обучающих примеров, нам надо поменять и λ, чтобы ослабление весов было тем же. Это значит, что мы меняем λ на 20,0. В таком случае получится следующее:
>>> net = network2.Network([784, 10]) >>> net.SGD(training_data[:1000], 30, 10, 10.0, lmbda = 20.0, \ ... evaluation_data=validation_data[:100], \ ... monitor_evaluation_accuracy=True) Epoch 0 training complete Accuracy on evaluation data: 12 / 100 Epoch 1 training complete Accuracy on evaluation data: 14 / 100 Epoch 2 training complete Accuracy on evaluation data: 25 / 100 Epoch 3 training complete Accuracy on evaluation data: 18 / 100 ...
Ага! У нас есть сигнал. Не особенно хороший, но есть. Это уже можно взять за отправную точку, и изменять гиперпараметры, чтобы попробовать получить дальнейшие улучшения. Допустим, мы решили, что нам надо поднять скорость обучения (как вы, наверно, поняли, решили мы неправильно, по причине, которую мы обсудим позднее, но давайте пока попробуем так сделать). Для проверки нашей догадки мы выкручиваем η до 100,0:
>>> net = network2.Network([784, 10]) >>> net.SGD(training_data[:1000], 30, 10, 100.0, lmbda = 20.0, \ ... evaluation_data=validation_data[:100], \ ... monitor_evaluation_accuracy=True) Epoch 0 training complete Accuracy on evaluation data: 10 / 100 Epoch 1 training complete Accuracy on evaluation data: 10 / 100 Epoch 2 training complete Accuracy on evaluation data: 10 / 100 Epoch 3 training complete Accuracy on evaluation data: 10 / 100 ...
Всё плохо! Судя по всему, наша догадка была неверна, и проблема была не в слишком низком значении скорости обучения. Пытаемся подкрутить η до небольшого значения 1,0:
>>> net = network2.Network([784, 10]) >>> net.SGD(training_data[:1000], 30, 10, 1.0, lmbda = 20.0, \ ... evaluation_data=validation_data[:100], \ ... monitor_evaluation_accuracy=True) Epoch 0 training complete Accuracy on evaluation data: 62 / 100 Epoch 1 training complete Accuracy on evaluation data: 42 / 100 Epoch 2 training complete Accuracy on evaluation data: 43 / 100 Epoch 3 training complete Accuracy on evaluation data: 61 / 100 ...
Вот так лучше! И так мы можем продолжать и далее, подкручивая каждый гиперпараметр, и постепенно улучшая эффективность. Изучив ситуацию и найдя улучшенное значение для η, мы переходим к поиску хорошего значения для λ. Затем проведём эксперимент с более сложной архитектурой, допустим, с сетью из 10 скрытых нейронов. Затем вновь подстроим параметры для η и λ. Затем увеличим сеть до 20 скрытых нейронов. Ещё немного подстроим гиперпараметры. И так далее, оценивая на каждом шаге эффективность при помощи части наших подтверждающих данных, и используя эти оценки для подбора всё лучших гиперпараметров. В процессе улучшений на то, чтобы увидеть влияние подстройки гиперпараметров, уходит всё больше времени, поэтому мы можем постепенно уменьшать частоту отслеживания.
В качестве общей стратегии такой подход выглядит многообещающе. Однако я хочу вернуться к тому первому шагу поиска гиперпараметров, позволяющих сети вообще хоть как-то обучиться. На самом деле, даже в приведённом примере ситуация получилась слишком оптимистичной. Работа с сетью, которая ничему не обучается, может оказаться чрезвычайно раздражающей. Можно по нескольку дней подстраивать гиперпараметры, и не получать осмысленных ответов. Поэтому я хотел бы ещё раз подчеркнуть, что на ранних стадиях нужно убедиться, что вы можете получать быструю обратную связь от экспериментов. Интуитивно может казаться, что упрощение проблемы и архитектуры вас лишь замедлит. На самом деле, это ускоряет процесс, поскольку вы сможете гораздо быстрее найти сеть с осмысленным сигналом. Получив такой сигнал, вы часто сможете получать быстрые улучшения при подстройке гиперпараметров. Как и во многих жизненных ситуациях, самым сложным бывает начать процесс.
Ладно, это общая стратегия. Теперь давайте взглянем на конкретные рекомендации по назначению гиперпараметров. Сконцентрируюсь на скорости обучения η, параметре регуляризации L2 λ, и размере мини-пакета. Однако многие замечания будут применимы и к другим гиперпараметрам, включая связанные с архитектурой сети, другими формами регуляризации, и некоторые гиперпараметры, с которыми мы познакомимся в книге далее, например, коэффициент импульса.
Скорость обучения
Допустим, мы запустили три сети MNIST с тремя разными скоростями обучения, η=0,025, η=0,25 и η=2,5, соответственно. Остальные гиперпараметры мы оставим такими, какие они были в прошлых разделах – 30 эпох, размер мини-пакета 10, λ=5,0. Мы также вернёмся к использованию всех 50 000 обучающих изображений. Вот график, показывающий поведение стоимости обучения (создан программой multiple_eta.py):
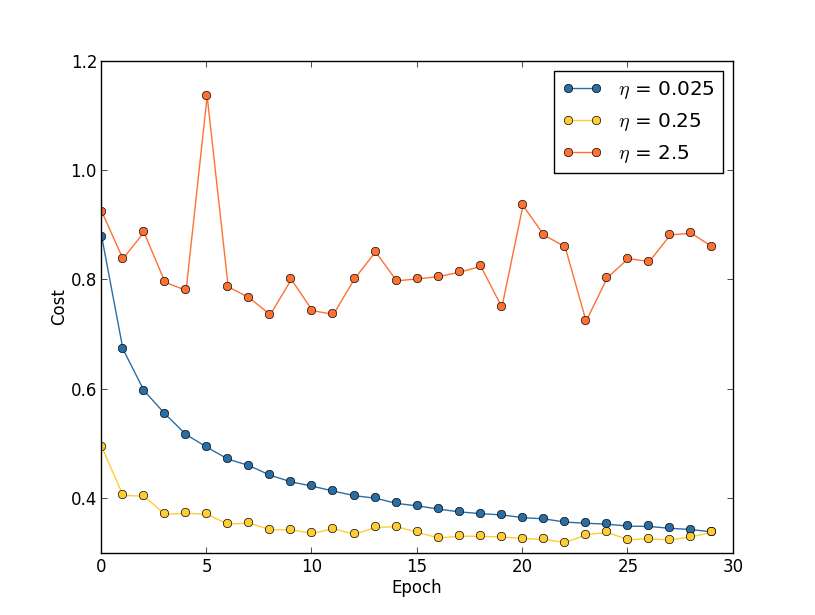
При η=0,025 стоимость уменьшается плавно до последней эпохи. С η=0,25 стоимость сначала уменьшается, однако после 20 эпох она насыщается, поэтому большая часть изменений оказываются малыми и, очевидно, случайными колебаниями. С η=2,5 стоимость сильно колеблется прямо с самого начала. Чтобы понять причину этих колебаний, вспомним, что стохастический градиентный спуск должен постепенно спускать нас в долину функции стоимости:
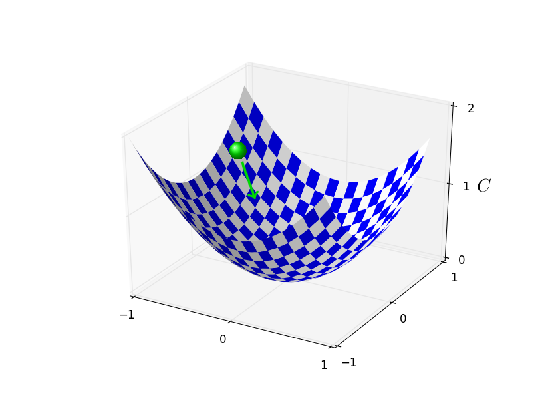
Данная картинка помогает интуитивно представить происходящее, но не является полным и всеобъемлющим объяснением. Если говорить точнее, но кратко, то градиентный спуск использует аппроксимацию первого порядка для функции стоимости, чтобы понять, как уменьшать стоимость. Для более крупных η становятся более важными члены функции стоимости более высокого порядка, и они могут доминировать в поведении, ломая градиентный спуск. Это особенно вероятно при приближении к минимумам и локальным минимумам функции стоимости, поскольку рядом с такими точками градиент становится маленьким, из-за чего членам более высокого порядка становится легче доминировать.
Однако, если η будет слишком крупной, то шаги будут такими большими, что могут перепрыгнуть минимум, из-за чего алгоритм будет карабкаться вверх из долины. Вероятно, именно это и заставляет стоимость осциллировать при η=2,5. Выбор η=0,25 приводит к тому, что начальные шаги действительно ведут нас по направлению к минимуму функции стоимости, и только когда мы подбираемся к нему, мы начинаем испытывать трудности с перепрыгиванием. А когда мы выбираем η=0,025, у нас таких трудностей в течение первых 30 эпох нет. Конечно, выбор такого малого значения η создаёт другую трудность – а именно, замедляет стохастический градиентный спуск. Лучшим подходом было бы начать с η=0,25, обучиться 20 эпох, а потом перейти к η=0,025. Позднее мы обсудим такую переменную скорость обучения. А пока остановимся на вопросе поиска одного подходящего значения для скорости обучения η.
Имея это в виду, мы можем выбрать η следующим образом. Сначала мы оцениваем пороговое значение η, при котором стоимость обучающих данных сразу начинает уменьшаться, а не колеблется и не увеличивается. Эта оценка не обязательно должна быть точной. Оценить порядок можно, начав с η=0,01. Если стоимость уменьшается в первые несколько эпох, то стоит последовательно пробовать η=0,1, затем 1,0, и так далее, пока не найдётся значение, при котором стоимость колеблется или увеличивается в первые эпохи. И наоборот, если стоимость колеблется или увеличивается в первые эпохи при η=0,01, тогда попробуйте η=0,001, η=0,0001, пока не найдёте значение, при котором стоимость уменьшается в первые несколько эпох. Эта процедура даст вам порядок порогового значения η. По желанию, вы можете уточнять вашу оценку, выбрав наибольшее значение для η, при котором стоимость уменьшается в первые эпохи, например, η=0,5 или η=0,2 (сверхточность тут не нужна). Это даёт нам оценку порогового значения η.
Реальное значение η, очевидно, не должно превышать выбранное пороговое. На самом деле, чтобы значение η оставалось полезным в течение многих эпох, вам лучше использовать значение раза в два меньше порогового. Такой выбор обычно позволит вам обучаться множество эпох без сильного замедления обучения.
В случае данных MNIST следование этой стратегии приведёт к оценке порогового порядка значения η в 0,1. После некоторых уточнений мы получим значение η=0,5. Следуя приведённому выше рецепту, нам следует использовать значение η=0,25 для нашей скорости обучения. Но на самом деле я обнаружил, что значение η=0,5 хорошо работало в течение 30 эпох, поэтому я не беспокоился по поводу его уменьшения.
Всё это выглядит довольно прямолинейно. Однако использование стоимости обучения для выбора η, кажется, противоречит тому, что я говорил ранее – что мы выбираем гиперпараметры, оценивая эффективность сети при помощи избранных подтверждающих данных. На самом деле мы будем использовать точность подтверждения, чтобы подобрать гиперпараметры регуляризации, размер мини-пакета и такие параметры сети, как количество слоёв и скрытых нейронов, и так далее. Почему мы делаем всё по-другому в случае скорости обучения? Честно говоря, этот выбор обусловлен моими личными эстетическими предпочтениями, и, вероятно, предвзят. Аргументация такова, что другие гиперпараметры должны улучшать конечную точность классификации на проверочном наборе, поэтому имеет смысл выбирать их на основе точности подтверждения. Однако скорость обучения лишь косвенно влияет на конечную точность классификации. Её основная цель – контролировать размер шага градиентного спуска, и отслеживать стоимость обучения наилучшим образом для того, чтобы распознавать слишком большой размер шага. Но всё же это личное эстетическое предпочтение. На ранних стадиях обучения стоимость обучения обычно уменьшается, только если увеличивается точность подтверждения, поэтому на практике не должно иметь значения то, какой критерий использовать.
Использование ранней остановки для определения количества эпох обучения
Как мы уже упоминали в этой главе, ранняя остановка означает, что в конце каждой эпохи нам нужно подсчитать точность классификации на подтверждающих данных. Когда она перестаёт улучшаться, прекращаем работу. В итоге установка количества эпох становится простым делом. В частности, это означает, что нам не надо специально выяснять, как количество эпох зависит от других гиперпараметров. Это происходит автоматически. Более того, ранняя остановка также автоматически не даёт нам переобучиться. Это, конечно, хорошо, хотя на ранних стадиях экспериментов может быть полезно отключить раннюю остановку, чтобы вы могли увидеть признаки переобучения и использовать их для подстройки подхода к регуляризации.
Для реализации РО нам нужно более конкретно описать, что означает «остановка улучшения точности классификации». Как мы видели, точность может очень сильно прыгать туда и сюда, даже когда общая тенденция улучшается. Если мы остановимся в первый раз, когда точность уменьшится, то мы почти наверняка не дойдём до возможных дальнейших улучшений. Подход лучше – прекратить обучение, если наилучшая точность классификации не улучшается достаточно долгое время. Допустим, к примеру, что мы занимаемся MNIST. Тогда мы можем решить прекратить процесс, если точность классификации не улучшалась за последние десять эпох. Это гарантирует, что мы не остановимся слишком рано, из-за неудачи при обучении, но и не будем ждать вечно каких-то улучшений, которые так и не произойдут.
Это правило «без улучшений за десять эпох» хорошо подходит для первичного исследования MNIST. Однако сети иногда могут выйти на плато близ определённой точности классификации, остаться там довольно долгое время, а потом снова начать улучшаться. Если вам нужно достичь очень хорошей эффективности, то правило «без улучшений за десять эпох» может быть для этого слишком агрессивным. Поэтому я рекомендую использовать правило «без улучшений за десять эпох» для первичных экспериментов, и постепенно принимает более мягкие правила, когда вы начнёте лучше понимать поведение вашей сети: «без улучшений за двадцать эпох», «без улучшений за пятьдесят эпох», и так далее. Конечно, это даёт нам ещё один гиперпараметр для оптимизации! Но на практике этот гиперпараметр обычно легко настроить для получения хороших результатов. А для задач, отличных от MNIST, правило «без улучшений за десять эпох» может оказаться слишком агрессивным, или недостаточно агрессивным, в зависимости от частностей конкретной задачи. Однако немного поэкспериментировав, обычно довольно легко найти подходящую стратегию ранней остановки.
Мы пока не использовали раннюю остановку в наших экспериментах с MNIST. Всё из-за того, что мы проводили много сравнений различных подходов к обучению. Для таких сравнений полезно использовать одинаковое количество эпох во всех случаях. Однако стоит изменить network2.py, введя в программу РО.
Задачи
- Измените network2.py так, чтобы там появилась РО по правилу «без изменений за n эпох», где n – настраиваемый параметр.
- Придумайте правило ранней остановки, отличное от «без изменений за n эпох». В идеале, правило должно искать компромисс между получением точности с высоким подтверждением и достаточно небольшим временем обучения. Добавьте правило в network2.py, и запустите три эксперимента по сравнению точностей подтверждения и количества эпох обучения с правилом «без изменений за 10 эпох».
План изменения скорости обучения
Пока мы держали скорость обучения η постоянной. Однако часто бывает полезно изменять её. На ранних этапах процесса обучения веса с большой вероятностью будут назначены совершенно неправильно. Поэтому лучше будет использовать большую скорость обучения, которая заставит веса меняться побыстрее. Затем можно уменьшить скорость обучения, чтобы сделать более тонкую подстройку весов.
Как нам наметить план изменения скорости обучения? Тут можно применять множество подходов. Один естественный вариант – использовать ту же базовую идею, что и в РО. Мы удерживаем скорость обучения постоянной, пока точность подтверждения не начнёт ухудшаться. Затем уменьшаем СО на некоторую величину, допустим, в два или в десять раз. Повторяем это много раз, до тех пор, пока СО не окажется в 1024 (или в 1000) раз меньше начальной. И заканчиваем обучение.
План изменения скорости обучения может улучшить эффективность, а также открывает огромные возможности по выбору плана. И это может стать головной болью – можно целую вечность провести за оптимизацией плана. Для первых экспериментов я бы предложил использовать одно, постоянное значение СО. Это даст вам хорошее первое приближение. Позже, Если вы захотите выжать из сети наилучшую эффективность, стоит поэкспериментировать с планом изменения скорости обучения так, как я это описал. В достаточно легко читаемой научной работе 2010 года демонстрируются преимущества переменных скоростей обучения при атаке на MNIST.
Упражнение
- Измените network2.py так, чтобы она реализовывала следующий план изменения скорости обучения: уполовинить СО каждый раз, когда точность подтверждения удовлетворяет правилу «без изменений за 10 эпох», и прекратить обучение, когда скорость обучения упадёт до 1/128 от начальной.
Параметр регуляризации λ
Я рекомендую начинать вообще без регуляризации (λ=0,0), и определить значение η, как указано выше. Используя выбранное значение η, мы затем можем использовать подтверждающие данные для выбора хорошего значения λ. Начите с λ=1,0 (хорошего аргумента в пользу именно такого выбора у меня нет), а потом увеличивайте или уменьшайте его в 10 раз, чтобы повышать эффективность в работе с подтверждающими данными. Найдя правильный порядок величины, можно подстраивать значение λ более точно. После этого нужно снова вернуться к оптимизации η.
Упражнение
- Возникает искушение использовать градиентный спуск, чтобы попытаться выучить хорошие значения для таких гиперпараметров, как λ и η. Можете ли вы догадаться о препятствии, не дающем использовать градиентный спуск для определения λ? Можете ли вы догадаться о препятствии, не дающем использовать градиентный спуск для определения η?
Как я выбрал гиперпараметры в начале книги
Если вы используете рекомендации из этого раздела, вы увидите, что подобранные значения η и λ не всегда точно соответствуют тем, что я использовал ранее. Просто у книги есть ограничения по тексту, из-за которых иногда было непрактично заниматься оптимизацией гиперпараметров. Вспомните обо всех сравнениях разных подходов к обучению, которыми мы занимались – сравнения квадратичной функции стоимости и перекрёстной энтропии, старых и новых методов инициализации весов, запуски с и без регуляризации, и так далее. Чтобы эти сравнения были осмысленными, я пытался не менять гиперпараметры между сравниваемыми подходами (или правильно их масштабировать). Конечно, нет причин для того, чтобы одни и те же гиперпараметры были оптимальными для всех разных подходов к обучению, поэтому используемые мною гиперпараметры были результатом компромисса.
В качестве альтернативы я бы мог попытаться оптимизировать все гиперпараметры для каждого подхода к обучению по максимуму. Это был бы более хороший и честный подход, поскольку мы бы взяли всё самое лучшее от каждого подхода к обучению. Однако мы провели десятки сравнений, и на практике это было бы слишком затратно с вычислительной точки зрения. Поэтому я решил остановиться на компромиссе, использовать достаточно хорошие (но не обязательно оптимальные) варианты гиперпараметров.
Размер мини-пакета
Как нужно выбирать размер мини-пакета? Для ответа на этот вопрос, давайте сначала предположим, что мы занимаемся онлайн-обучением, то есть, используем мини-пакет размера 1.
Очевидная проблема с онлайн-обучением состоит в том, что использование мини-пакетов, состоящих из единственного обучающего примера, приведёт к серьёзным ошибкам в оценке градиента. Но на самом деле эти ошибки не представят такой уж серьёзной проблемы. Причина в том, что отдельные оценки градиента не должны быть сверхточными. Нам лишь нужно получить достаточно точную оценку для того, чтобы наша функция стоимости снижалась. Это как если бы вы пытались попасть на северный магнитный полюс, но у вас был бы ненадёжный компас, при каждом измерении ошибающийся на 10-20 градусов. Если вы будете достаточно часто сверяться с компасом, и в среднем он будет указывать верное направление, вы в итоге сможете добраться до северного магнитного полюса.
Если учитывать этот аргумент, кажется, что нам стоит использовать онлайн-обучение. Но на самом деле ситуация оказывается несколько более сложной. В задаче к последней главе я указал, что для вычисления обновления градиента для всех примеров в мини-пакете одновременно можно использовать матричные техники, а не цикл. В зависимости от подробностей вашего железа и библиотеки для линейной алгебры может оказаться гораздо быстрее вычислять оценку для мини-пакета размером, допустим, 100, чем вычислять оценку градиента для мини-пакета в цикле для 100 обучающих примеров. Это может оказаться, допустим, всего в 50 раз медленнее, а не в 100.
Сперва кажется, что это нам не сильно помогает. С размером мини-пакета в 100 правило обучения для весов выглядит, как:
где суммирование идёт по обучающим примерам в мини-пакете. Сравните с
для онлайн-обучения. Даже если на обновление мини-пакета уйдёт в 50 раз больше времени, всё равно онлайн-обучение кажется лучшим вариантом, поскольку обновляться мы будем гораздо чаще. Но допустим, однако, что в случае с мини-пакетом мы увеличили скорость обучения в 100 раз, тогда правило обновления превращается в:
Это похоже на 100 отдельных ступеней онлайн-обучения со скоростью обучения η. Однако на одну ступень онлайн-обучения уходит всего в 50 раз больше времени. Конечно, на самом деле это не ровно 100 ступеней онлайн-обучения, поскольку в мини-пакете все ∇Cx оцениваются для одного и того же набора весов, в отличие от кумулятивного обучения, происходящего в онлайн-случае. И всё же кажется, что использование более крупных мини-пакетов ускорит процесс.
Учитывая все эти факторы, выбор лучшего размера мини-пакета – это компромисс. Выберете слишком маленький, и не получите всё преимущество хороших матричных библиотек, оптимизированных для быстрого железа. Выберете слишком большой, и не будете обновлять веса достаточно часто. Вам необходимо выбрать компромиссное значение, максимизирующее скорость обучения. К счастью, выбор размера мини-пакета, при котором скорость максимизируется, относительно независима от других гиперпараметров (кроме общей архитектуры), поэтому, чтобы найти хороший размер мини-пакета, не обязательно их оптимизировать. Следовательно, достаточно будет использовать приемлемые (не обязательно оптимальные) значения у других гиперпараметров, а потом попробовать несколько разных размеров мини-пакетов, масштабируя η, как указано выше. Постройте график зависимости точности подтверждения от времени (реального прошедшего времени, не эпох!), и выбирайте размер мини-пакета, дающий наиболее быстрое улучшение быстродействия. С выбранным размером мини-пакета можете перейти к оптимизации других гиперпараметров.
Конечно, как вы уже, без сомнения, поняли, в нашей работе такой оптимизации я не проводил. В нашей реализации НС вообще не используется быстрый подход к обновлению мини-пакетов. Я просто использовал размер мини-пакета 10, не комментируя и не объясняя его, почти во всех примерах. А вообще мы могли бы ускорить обучение, уменьшив размер мини-пакета. Я этого не делал, в частности, потому, что мои предварительные эксперименты предполагали, что ускорение будет довольно скромным. Но в практических реализациях нам бы однозначно хотелось реализовать наиболее быстрый подход к обновлениям мини-пакетов, и попытаться оптимизировать их размер, чтобы максимизировать общую скорость.
Автоматизированные техники
Я описывал эти эвристические подходы, как нечто, что нужно подстраивать руками. Ручная оптимизация – хороший способ получить представление о работе НС. Однако, и, впрочем, неудивительно, огромная работа уже проделана над автоматизацией этого проекта. Распространённой техникой является поиск по решётке, систематически просеивающий решётку в пространстве гиперпараметров. Обзор достижений и ограничений этой техники (а также рекомендации по легко реализуемым альтернативам) можно найти в работе 2012 года. Было предложено множество сложных техник. Не буду делать обзор их всех, но хочу отметить многообещающую работу 2012 года, использовавшую байесовскую оптимизацию гиперпараметров. Код из работы открыт всем, и с определённым успехом использовался и другими исследователями.
Суммируем
Пользуясь практическими правилами, которые я описал, вы не получите от своей НС совершенно наилучшие результаты из всех возможных. Но они, вероятно, обеспечат вам хорошую отправную точку и фундамент для дальнейших улучшений. В частности, я в основном описывал гиперпараметры независимо. На практике между ними существует связь. Вы можете экспериментировать с η, решить, что нашли правильное значение, потом начать оптимизировать λ, и обнаружить, что это нарушает вашу оптимизацию η. На практике полезно двигаться в разные стороны, постепенно приближаясь к хорошим значениям. Превыше прочего учтите, что описанные мною эвристические подходы – это простые практические правила, но не нечто, вырезанное в камне. Вам нужно искать признаки того, что что-то не работает, и иметь желание экспериментировать. В частности, тщательно отслеживать поведение вашей нейросети, особенно точность подтверждения.
Сложность выбора гиперпараметров усугубляется тем, что практические знания по их выбору размазаны по множеству исследовательских работ и программ, а часто находятся только в головах отдельных практиков. Существует огромное множество работ с описаниями того, как следует поступать (часто противоречащие друг другу). Однако существует несколько особенно полезных работ, синтезирующих и выделяющих крупную часть этих знаний. В работе Йошуа Бенджио от 2012 года даются практические рекомендации по использованию обратного распространения и градиентного спуска для обучения НС, включая и глубокие НС. Множество деталей Бенджио описывает гораздо подрбонее. Чем я, включая систематический поиск гиперпараметров. Ещё одна хорошая работа – работа 1998 года Йанна Лекуна и др. Обе работы появляются в чрезвычайно полезной книге 2012 года, где собрано множество трюков, часто используемых в НС: "Нейросети: хитрости ремесла". Книжка дорогая, но многие её статьи были выложены в интернет их авторами, и их можно найти в поисковиках.
Из этих статей, и, особенно из собственных экспериментов, становится ясно одно: задачу оптимизации гиперпараметров нельзя назвать полностью решённой. Всегда существует ещё один трюк, который можно попробовать для улучшения эффективности. У писателей есть поговорка, что книгу нельзя закончить, а можно только бросить. То же верно и для оптимизации НС: пространство гиперпараметров настолько огромно, что оптимизацию нельзя закончить, а можно лишь прекратить, оставив НС потомкам. Так что вашей целью будет разработка рабочего процесса, позволяющего вам быстро провести неплохую оптимизацию, и при этом оставляющего вам возможность по необходимости попробовать более детальные варианты оптимизации.
Трудности с подбором гиперпараметров заставляют некоторых людей жаловаться, что НС требуют слишком много усилий по сравнению с другими техниками МО. Я слышал много вариантов жалоб типа: «Да, хорошо настроенная НС может выдать наилучшую эффективность при решении задачи. Но, с другой стороны, я могу попробовать случайный лес [или SVM, или любую другую вашу любимую технологию], и она просто работает. У меня нет времени разбираться с тем, какая НС мне подойдёт». Конечно, с практической точки зрения хорошо иметь под ругой лёгкие в применении техники. Это особенно хорошо, когда вы только начинаете работать с задачей, и ещё непонятно, может ли вообще МО помочь её решить. С другой стороны, если вам важно достичь оптимальных результатов, вам может понадобиться испытать несколько подходов, требующих более специальных знаний. Было бы здорово, если бы МО всегда было лёгким делом, но не существует причин, по которым оно априори должно быть тривиальным.
Другие техники
Каждая из техник, проработанных в этой главе, ценна сама по себе, но это не единственная причина, по которой я их описал. Более важно ознакомиться с некоторыми из проблем, которые могут встретиться в области НС, и со стилем анализа, который может помочь их преодолеть. В каком-то смысле, мы учимся тому, как размышлять о НС. В оставшейся части главы я кратко опишу набор других техник. Их описания будут не такими глубокими, как у предыдущих, но должны передать некие ощущения, касающиеся разнообразия техник, встречающихся в области НС.
Вариации стохастического градиентного спуска
Стохастический градиентный спуск через обратное распространение хорошо послужил нам во время атаки на задачу классификации рукописных цифр из MNIST. Однако к оптимизации функции стоимости есть множество других подходов, и иногда они показывают эффективность, превосходящую таковую у стохастического градиентного спуска с мини-пакетами. В данной секции я кратко опишу два таких подхода, гессиан и импульс.
Гессиан
Для начала давайте отложим в сторону НС. Вместо этого просто рассмотрим абстрактную проблему минимизации функции стоимости C от многих переменных, w=w1,w2,…, то есть, C=C(w). По теореме Тейлора функцию стоимости в точке w можно аппроксимировать:
Мы можем переписать это компактнее, как
где ∇C – обычный вектор градиента, а H – матрица, известная, как матрица Гессе, на месте jk в которой находится ∂2C/∂wj∂wk. Допустим, мы аппроксимируем C, отказавшись от членов высшего порядка, скрывающихся за многоточием в формуле:
Используя алгебру, можно показать, что выражение с правой стороны можно минимизировать, выбрав:
Сторого говоря, для того, чтобы это был именно минимум, а не просто экстремум, нужно предположить, что матрица Гессе определеннее положительна. Интуитивно это значит, что функция С похожа на долину, а не на гору или седловину.
Если (105) будет хорошим приближением к функции стоимости, стоит ожидать, что переход от точки w к точке w+Δw=w−H−1∇C должен значительно уменьшить функцию стоимости. Это предлагает возможный алгоритм минимизации стоимости:
- Выбрать начальную точку w.
- Обновить w до новой точки, w′=w−H−1∇C, где гессиан H и ∇C вычисляются в w.
- Обновить w' до новой точки, w′′=w′−H′−1∇′C, где гессиан H и ∇C вычисляются в w'.
- …
На практике, (105) является лишь приближением, и лучше брать шаги поменьше. Мы сделаем это, постоянно обновляя w на величину Δw=−ηH−1∇C, где η — это скорость обучения.
Такой подход к минимизации функции стоимости известен, как оптимизация Гессе. Существуют теоретические и эмпирические результаты, показывающие, что методы Гессе сходятся к минимуму за меньшее количество шагов, чем стандартный градиентный спуск. В частности, посредством включения информации об изменениях второго порядка в функции стоимости, в подходе Гессе возможно избежать многих патологий, встречающихся в градиентном спуске. Более того, существуют версии алгоритма обратного распространения, которые можно использовать для вычисления гессиана.
Если оптимизация Гессе такая классная, что же мы не используем её в наших НС? К сожалению, хотя у неё много желанных свойств, есть и одно очень нежелательное: её очень сложно применять на практике. Часть проблемы – огромный размер матрицы Гессе. Допустим, у нас есть НС с 107 весов и смещений. Тогда в соответствующей матрице Гессе будет 107 × 107 = 1014 элементов. Слишком много! В итоге вычислять H−1∇C на практике получается очень сложно. Но это не значит, что о ней бесполезно знать. Множество вариантов градиентного спуска вдохновлено оптимизацией Гессе, они просто избегают проблемы чрезмерно больших матриц. Давайте взглянем на одну такую технику, градиентный спуск на основе импульса.
Градиентный спуск на основе импульса
Интуитивно, преимущество оптимизации Гессе состоит в том, что она включает не только информацию о градиенте, но и информацию о его изменении. Градиентный спуск на основе импульса основан на схожей интуиции, однако избегает крупных матриц из вторых производных. Чтобы понять технику импульса, вспомним нашу первую картинку градиентного спуска, в которой мы рассматривали шар, скатывающийся в долину. Тогда мы увидели, что градиентный спуск, вопреки своему имени, лишь немного напоминает шар, падающий на дно. Техника импульса изменяет градиентный спуск в двух местах, что делает его более похожим на физическую картину. Во-первых, она вводит понятие «скорости» для параметров, которые мы пытаемся оптимизировать. Градиент пытается изменить скорость, а не «местоположение» напрямую, похоже на то, как физические силы меняют скорость, и лишь косвенно влияют на местоположение. Во-вторых, метод импульса представляет нечто вроде члена для трения, который постепенно уменьшает скорость.
Давайте дадим более математически точное определение. Введём переменные скорости v=v1,v2,…, по одной на каждую соответствующую переменную wj (в нейросети эти переменные, естественно, включают все веса и смещения). Затем мы меняем правило обновления градиентного спуска w→w′ = w−η∇C на
В уравнениях μ — это гиперпараметр, управляющий количеством торможения, или трения системы. Чтобы понять смысл уравнений, сначала полезно рассмотреть случай, в котором μ=1, то есть, когда трение отсутствует. В таком случае изучение уравнений показывает, что теперь «сила» ∇C меняет скорость v, а скорость управляет скоростью изменения w. Интуитивно, скорость можно набрать, постоянно добавляя к ней члены градиента. Это значит, что если градиент движется примерно в одном направлении в течение нескольких этапов обучения, мы можем набрать достаточно большую скорость движения в этом направлении. Представьте, к примеру, что происходит при движении вниз по склону:

С каждым шагом вниз по склону скорость увеличивается, и мы движемся всё быстрее и быстрее ко дну долины. Это позволяет технике скорости работать гораздо быстрее, чем стандартному градиентному спуску. Конечно, проблема в том, что, достигнув дна долины, мы его проскочим. Или, если градиент будет меняться слишком быстро, могло бы оказаться, что мы движемся в обратном направлении. В этом и смысл введения гиперпараметра μ в (107). Ранее я сказал, что μ управляет количеством трения в системе; точнее, количество трения нужно представлять себе в виде 1-μ. Когда μ=1, как мы увидели, трения нет, и скорость полностью определяется градиентом ∇C. И наоборот, когда μ=0, трения очень много, скорость не набирается, и уравнения (107) и (108) сводятся к обычным уравнениям градиентного спуска, w→w′ = w−η∇C. На практике, использование значения μ в промежутке между 0 и 1 может дать нам преимущество возможности набора скорости без опасности проскочить минимум. Такое значение для μ мы можем выбрать при помощи отложенных подтверждающих данных примерно так же, как выбирали значения для η и λ.
Пока я избегал присваивания имени гиперпараметру μ. Дело в том, что стандартное имя для μ было выбрано плохо: он называется коэффициентом импульса. Это может сбить вас с толку, поскольку μ совсем не похож не понятие импульса из физики. Он куда сильнее связан с трением. Однако термин «коэффициент импульса» широко используется, поэтому мы тоже продолжим его использовать.
Приятная особенность техники импульса заключается в том, что для изменения реализации градиентного спуска с целью включить в неё эту технику не требуется почти ничего делать. Мы всё ещё можем использовать обратное распространение для подсчёта градиентов, как и ранее, и использовать такие идеи, как проверка стохастически выбранных мини-пакетов. В этом случае мы можем получить некоторые преимущества оптимизации Гессе, используя информацию об изменении градиента. Однако всё это происходит без недостатков, и лишь с небольшими изменениями кода. На практике техника импульса широко используется и часто помогает ускорять обучение.
Упражнения
- Что пойдёт не так, если мы будем использовать μ>1 в технике импульса?
- Что пойдёт не так, если мы будем использовать μ<0 в технике импульса?
Задача
- Добавьте стохастический градиентный спуск на основе импульса в network2.py.
Другие подходы к минимизации функции стоимости
Было разработано и множество других подходов к минимизации функции стоимости, и по поводу наилучшего подхода согласия не достигнуто. Углубляясь в тему нейросетей, полезно покопаться и в других технологиях, понять, как они работают, какие у них сильные и слабые стороны, и как применять их на практике. В упомянутой мною ранее работе вводятся и сравниваются несколько таких техник, включая спаренный градиентный спуск и метод BFGS (а также изучите близко связанный с ним метод BFGS с ограничением памяти, или L-BFGS). Ещё одна технология, недавно показавшая многообещающие результаты, это ускоренный градиент Нестерова, улучшающая технику импульса. Однако для многих задач хорошо работает простой градиентный спуск, особенно при использовании импульса, поэтому мы будем придерживаться стохастического градиентного спуска до конца книги.
Другие модели искусственного нейрона
Пока что мы создавали наши НС с использованием сигмоидных нейронов. В принципе, НС, построенная на сигмоидных нейронах, может вычислить любую функцию. Но на практике сети, построенные на других моделях нейронов, иногда опережают сигмоидные. В зависимости от применения, сети, основанные на таких альтернативных моделях, могут быстрее обучаться, лучше обобщать на проверочные данные, или делать и то, и другое. Давайте я упомяну парочку альтернативных моделей нейронов, чтобы дать вам представление о некоторых широко применяемых вариантах.
Возможно, простейшей вариацией будет танг-нейрон, заменяющий сигмоидную функцию гиперболическим тангенсом. Выход танг-нейрона со входом x, вектором весов w и смещением b задаётся, как
где tanh, естественно, гиперболический тангенс. Оказывается, что он очень близко связан с сигмоидным нейроном. Чтобы это увидеть, вспомним, что tanh определяется, как
Применив немного алгебры, легко видеть, что
то есть, tanh – это просто масштабирование сигмоиды. Графически также можно видеть, что у функции tanh та же форма, что и у сигмоиды:
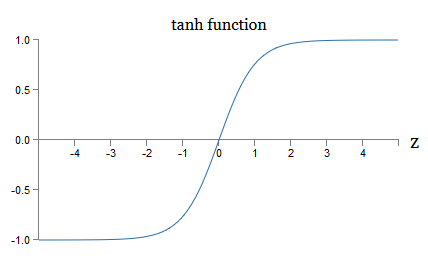
Одно различие между танг-нейронами и сигмоидными нейронами состоит в том, что выход первых простирается от -1 до 1, а не от 0 до 1. Это значит, что при создании сети на основе танг-нейронов вам может понадобиться нормализовать ваши выходы (и, в зависимости от деталей применения, возможно, и входы) немного не так, как в сигмоидных сетях.
Как и сигмоидные, танг-нейроны, в принципе, могут подсчитать любую функцию (хотя с этим и существуют некоторые подвохи), размечая входы от -1 до 1. Более того, идеи обратного распространения и стохастического градиентного спуска точно так же легко применять к танг-нейронам, как и к сигмоидным.
Упражнение
- Докажите уравнение (111).
Нейрон какого типа стоит использовать в сетях, танг или сигмоидный? Ответ, мягко говоря, неочевиден! Однако существуют теоретические аргументы и некоторые эмпирические свидетельства того, что танг-нейроны иногда работают лучше. Давайте кратенько пройдёмся по одному из теоретически аргументов в пользу танг-нейронов. Допустим, мы используем сигмоидные нейроны, и все активации в сети будут положительными. Рассмотрим веса wl+1jk, входящие для нейрона №j в слое №l+1. Правила обратного распространения (BP4) говорят нам, что связанный с этим градиент будет равен alkδl+1j. Поскольку активации положительны, знак этого градиента будет таким же, как у δl+1j. Это означает, что если δl+1j положительна, тогда все веса wl+1jk будут уменьшаться во время градиентного спуска, а если δl+1j отрицательна, тогда все веса wl+1jk будут увеличиваться во время градиентного спуска. Иначе говоря, все веса, связанные с одним и тем же нейроном, будут либо увеличиваться, либо уменьшаться совместно. А это проблема, поскольку, возможно, потребуется увеличивать некоторые веса, уменьшая другие. Но это может произойти, только усли у некоторых входных активаций будут разные знаки. Что говорит о необходимости замены сигмоиды другой функцией активации, например, гиперболическим тангенсом, позволяющей активациям быть как положительными, так и отрицательными. И действительно, поскольку tanh симметричен относительно нуля, tanh(−z) = −tanh(z), можно ожидать, что, грубо говоря, активации в скрытых слоях будут поровну распределены между положительными и отрицательными. Это поможет гарантировать отсутствие систематического смещения в обновлениях весов в ту или иную сторону.
Насколько серьёзно стоит рассматривать этот аргумент? Ведь он эвристический, не даёт строгого доказательства того, что танг-нейроны превосходят сигмоидные. Возможно, у сигмоидных нейронов есть некие свойства, компенсирующие эту проблему? И действительно, во многих случаях функция tanh показала от минимальных до никаких преимуществ по сравнению с сигмоидой. К сожалению, у нас не существует простых и быстро реализуемых способов проверить, нейрон какого типа будет обучаться быстрее или покажет себя эффективнее в обобщении для какого-то конкретного случая.
Другой вариант сигмоидного нейрона – выпрямленный линейный нейрон, или выпрямленная линейная единица [rectified linear unit, ReLU]. Выход ReLU со входом x, вектором весов w и смещением b задаётся так:
Графически выпрямляющая функция max(0,z) выглядит так:
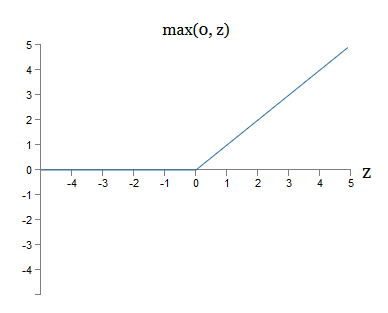
Такие нейроны, очевидно, сильно отличаются и от сигмоидных, и от танг-нейронов. Однако они похожи в том, что тоже могут быть использованы для вычисления любой функции, и их можно обучать, используя обратное распространение и стохастический градиентный спуск.
Когда нужно использовать ReLU вместо сигмоидных или танг-нейронов? В последних работах по распознаванию изображений (1, 2, 3, 4) были обнаружены серьёзные преимущества использования ReLU почти по всей сети. Однако, как и с танг-нейронами, у нас пока нет по-настоящему глубокого понимания того, когда именно ReLU будут предпочтительнее, и почему. Чтобы получить некое представление о некоторых проблемах, вспомните, что сигмоидные нейроны прекращают обучаться при насыщении, то есть, когда выход близок к 0 или 1. Как мы уже много раз видели в этой главе, проблема состоит в том, что члены σ' уменьшают градиент, что замедляет обучение. Танг-нейроны страдают от похожих трудностей при насыщении. При этом увеличение взвешенного входа на ReLU никогда не заставит его насытиться, поэтому соответственного замедления обучения не произойдёт. С другой стороны, когда взвешенный ввод на ReLU будет отрицательным, градиент исчезает, и нейрон вообще перестаёт обучаться. Это лишь пара из множества проблем, делающих нетривиальной задачу понимания того, когда и как ReLU ведут себя лучше сигмоидных или танг-нейронов.
Я нарисовал картину неопределённости, подчёркивая, что у нас пока нет твёрдой теории выбора функций активации. И действительно, эта проблема ещё сложнее, чем я описал, поскольку возможных функций активации существует бесконечно много. Какая из них даст нам наиболее быстро обучающуюся сеть? Какая даст наибольшую точность в тестах? Я удивлён, насколько мало было по-настоящему глубоких и систематических исследований этих вопросов. В идеале у нас должна быть теория, подробно говорящая нам о том, как выбирать (и, возможно, на лету менять) наши функции активации. С другой стороны, нас не должно останавливать отсутствие полноценной теории! У нас уже есть мощные инструменты, и с их помощью мы можем достичь значительного прогресса. До конца книги я буду использовать сигмоидные нейроны в качестве основных, поскольку они хорошо работают и дают конкретные иллюстрации ключевых идей, относящихся к НС. Но учитывайте, что те же самые идеи можно применять и к другим нейронам, и в этих вариантах есть свои преимущества.
Истории из мира нейросетей
Вопрос: какой подход вы применяете при использовании и исследовании техник МО, которые поддерживаются практически исключительно эмпирическими наблюдениями, а не математикой? В какой ситуации вы сталкивались с отказом таких техник?
Ответ: вам нужно понять, что наши теоретические инструменты весьма слабы. Иногда у нас появляется хорошая математическая интуиция по поводу того, почему определённая техника должна сработать. Иногда интуиция изменяет нам. В итоге вопросы превращаются в следующие: насколько хорошо мой метод сработает на этой конкретной задаче, и насколько велик набор задач, на котором он хорошо работает?
— Вопросы и ответы с исследователем нейросетей Яном Лекуном
Однажды на конференции по основам квантовой механики, я заметил то, что мне показалось забавной речевой привычкой: по окончанию доклада вопросы аудитории часто начинались с фразы: «Мне очень импонирует ваша точка зрения, но…». Квантовые основы – не совсем моя обычная область, и я обратил внимание на такой стиль задавания вопросов потому, что на других научных конференциях я практически не встречался с тем, чтобы спрашивающий выказывал симпатию к точке зрения докладчика. В то время я решил, что преобладание таких вопросов говорило о том, что прогресса в квантовых основах было достигнуто довольно мало, и люди просто только начинали набирать обороты. Позднее я понял, что эта оценка была слишком жёсткой. Докладчики боролись с одними из самых сложных проблем, с которыми только сталкивались человеческие умы. Естественно, что прогресс шёл медленно! Однако всё равно существовала ценность в том, чтобы услышать новости о мышлении людей, касающемся этой области, даже если у них не было практически ничего нового.
В данной книге вы могли заметить «нервный тик», сходный с фразой «мне весьма импонирует». Чтобы объяснить, что мы имеем, я часто прибегал к словам вроде «эвристически» или «грубо говоря», за которыми следовало объяснение того или иного явления. Эти истории правдоподобны, но эмпирические свидетельства часто были весьма поверхностны. Если вы изучите исследовательскую литературу, то увидите, что истории подобного толка появляются во многих исследовательских работах, посвящённых нейросетям, часто в компании малого количества поддерживающих их свидетельств. Как нам относиться к таким историям?
Во многих областях науки – особенно там, где рассматриваются простые явления – можно найти очень строгие и надёжные свидетельства весьма общим гипотезам. Но в НС есть огромное количество параметров и гиперпараметров, и существуют чрезвычайно сложные взаимоотношения между ними. В таких невероятно сложных системах неимоверно сложно делать надёжные общие заявления. Понимание НС во всех их полноте, как квантовые основы, испытывает пределы человеческого разума. Часто нам приходится обходиться свидетельствами в пользу или против нескольких определённых частных случаев общего заявления. В итоге эти заявления иногда требуется менять или отказываться от них, поскольку появляются новые свидетельства.
Один из подходов к этой ситуации – считать, что любая эвристическая история про НС подразумевает некий вызов. К примеру, рассмотрим процитированное мною объяснение того, почему работает исключение (dropout) из работы 2012 года: «Эта техника уменьшает сложную совместную адаптацию нейронов, поскольку нейрон не может полагаться на присутствие определённых соседей. В итоге ему приходиться обучаться более надёжным признакам, которые могут быть полезными в совместной работе со многими различными случайными подмножествами нейронов». Богатое и провокационное заявление, на базе которого можно построить целую исследовательскую программу, в которой нужно будет выяснять, в чём оно правдиво, где ошибается, а что требует уточнений и изменений. И сейчас действительно существует целая индустрия исследователей, изучающих исключение (и множество его вариантов), пытающихся понять, как оно работает, и какие ограничения имеет. Так и со многими другими эвристическими подходами, которые мы обсуждали. Каждый из них – не только потенциальное объяснение, но и вызов к исследованию и более детальному пониманию.
Конечно, ни у одного человека не хватит времени исследовать все эти эвристические объяснения достаточно глубоко. У всего сообщества исследователей НС уйдут десятилетия на то, чтобы разработать реально мощную теорию обучения НС, основанную на доказательствах. Значит ли это, что стоит отвергать эвристические объяснения, как нестрогие и не имеющие достаточно доказательств? Нет! Нам нужна такая эвристика, которая будет вдохновлять наше мышление. Это похоже на эпоху великих географических открытий: ранние исследователи часто действовали (и совершали открытия) на основе верований, ошибавшихся серьёзнейшим образом. Позднее мы исправляли эти заблуждения, пополняя свои географические знания. Когда вы плохо что-то понимаете – как понимали исследователи географию, и как сегодня мы понимаем НС – важнее смело изучать неизвестное, чем быть скрупулёзно правым на каждом шагу ваших рассуждений. Поэтому вы должны рассматривать эти истории как полезную инструкцию к тому, как размышлять о НС, поддерживая здоровую осведомлённость об их ограничениях, и тщательно отслеживая надёжность свидетельств в каждом случае. Иначе говоря, хорошие истории нужны нам для мотивации и вдохновения, а скрупулёзные тщательные расследования – для того, чтобы открывать реальные факты.
