
Прочие статьи цикла
В работе рассматривается традиционный подход, который автором в ряде статей критикуется.
Здесь я воздержусь от критики, и направлю свои усилия на разъяснение сложных моментов в традиционном подходе. Весь арсенал существующих методов не решает задачу факторизации в принципе, так как почти все решеточные и другие алгоритмы построены на жесткой связи и зависимости времени их выполнения от разрядности факторизуемого числа N. Но замечу, что у чисел имеются и другие свойства кроме разрядности, которые можно использовать в алгоритмах факторизации.
Оценки сложности — эвристические опираются на рассуждения ограниченные авторским пониманием проблемы. Пора бы уже понять, что факторизация чисел в глубоком тупике, а математикам (не только им) пересмотреть свое отношение к проблеме и создать новые модели.
Простая идея факторизации целого нечетного числа N исторически — состоит в поиске пары квадратов чисел разной четности, разность которых кратна kN, при k =1 разложение успешно реализуется так как в этом случае сразу получаем произведение двух скобок
Таким образом, проблема факторизации преобразуется в проблему поиска подходящих квадратов чисел. Понимали эти факты многие математики, но П. Ферма первым в 1643 году реализовал идею поиска таких квадратов в алгоритме, названном его именем. Перепишем иначе приведенное соотношение
Если разность слева от равенства не равна квадрату, то изменяя х, можно подобрать другой квадрат, чтобы и справа получался квадрат. Практически все нынешние алгоритмы используют эту идею (поиска пары квадратов), но судя по результатам, похоже, что идея себя исчерпала.
Предпосылки и возможности
Криптография с открытым ключом (асимметрические криптосистемы) ныне стала уже повседневностью, хотя совсем небольшой временной период (в историческом плане) отделяет нас от момента ее открытия. К основным ее отличиям от симметричной криптографии следует в первую очередь отнести возможность использования для передачи (шифрованных текстов (ШТ), других сообщений) незащищенных каналов в сетях информационного обмена, цифровую подпись, аутентификацию.
Математической основой этих фактов и явлений служат:
— односторонняя (однонаправленная) функция;
— односторонняя функция с лазейкой (с секретом).
Определение. Функция f: X → Y называется односторонней, если существует эффективный алгоритм ее вычисления при любом Х, но не существует такого алгоритма для вычисления обратной к ней функции.
Определение. Функция f: X → Y называется односторонней с секретом (с лазейкой, потайным ходом, trapdoor), если при наличии некоторой дополнительной информации (ключа) возможен эффективный алгоритм ее обращения. Под эффективным алгоритмом понимают полиномиальный в отличие от экспоненциального.
Математикам давно знакома проблема факторизации и они ищут пути ее эффективного решения. К основным достижениям (результатам) математики в области факторизации чисел следует отнести следующее:
— метод Евклида отыскания наибольшего общего делителя (НОД), в котором для пары чисел b и а, если они составные, но взаимно простые, НОД (а, b)=1. Но если эти числа имеют общий делитель, то алгоритм НОД находит больший из всех делитель d и НОД (а, b)=d.
— другой важный результат, которым располагает математика, состоит в том, что любое составное нечетное целое число N представимо разностью квадратов целых чисел разной четности
— метод факторизации П. Ферма известен с 1643 года. Он находит наибольший множитель d числа N, не превосходящий
— решето Эратосфена.
Метод линейного решета (алгоритм LS)
Рихард Шрёппель (Richard Schroeppel), занимаясь проблемой факторизации чисел, предложил оригинальный алгоритм для генерации соотношений следующего вида
На числовом интервале
где
В силу сравнимости
Допустим, что правая часть сравнения может быть представлена произведением и левая часть будет полным квадратом, если величины
где рi простые числа из факторной базы S, а Δ – целое число, являющееся полным квадратом.
В такой ситуации сравнение с произведениями по модулю N соответствует сравнению
Если это достигается, то возможно построить, используя алгоритм гауссова исключения, сравнение
Для формирования величин (a, b) существует эффективный способ, называемый решетом, поиска значений
И сами величины (a, b) принимают небольшие значения. Значения
Проверка делимости величины s (a, b) на простое число р для произвольных a, b∈ I сводится к проверке делимости на р величины
Это легко показывается. Пусть простое число р ∈ S делит значение величины s (a, b) при некоторых а. Но из равенства
Существенным недостатком метода является необходимость большого объема памяти, и отсутствие алгоритмического способа построения сравнений с известным разложением левой части в произведение множителей из факторной базы. Этот текст (компиляция) заимствован из разных публикаций, но практически не сопровождается моими комментариями. Для сравнения привожу другой текст о методе QS, но сопровождаю комментариями, которые, как я надеюсь, вносят понимание и ясность.
Квадратичное решето (QS)
Этот алгоритм (quadratic sieve-QS) предложен в 1981 году Карлом Померансом и почти 10 лет был лучшим (до предложенного в 1990 алгоритма SNFS (special number field sieve), обеспечившего разложение на множители 9-го числа П.Ферма
Возможности квадратичного решета ограничиваются разложением в сомножители чисел, с не более чем 110 десятичных цифр в их описании. Оценка сложности (эвристическая) алгоритма даже после многочисленных усовершенствований составляет
При рассмотрении QS важными понятиями, которые желательно удерживать в уме, являются:
— вектор показателей степеней чисел -<4 0 1 1>, где, например, для имеем
— линейная зависимость векторов (см. пример 3 здесь);
— факторная база S=(2,3,5,7) набор малых простых чисел, для которых N -квадратичный вычет;
— гладкие числа
— процедура просеивания.
Целью метода QS является факторизация натурального числа N путем получения для чисел х и у, множество которых строится специальным образом, соотношения
Делители p и q отыскиваются с помощью специальных чисел-значений многочлена вида
Очевидно, что увеличение значения М приведет к увеличению множества чисел х для просеивания, что способствует росту множества гладких чисел. Но при этом возрастает и время просеивания. Аналогичные проблемы возникают и при увеличении факторной базы S-больше элементов в S-дольше идет обработка таблиц Д и Q (в последней опущены аргументы х).
Определение. Факторная база S — набор малых простых чисел, включающий р =-1 и все простые числа рi, рi≤В, такие, что символ Лежандра (N/pi)=+1, т.е. N является квадратичным вычетом для всех рi из факторной базы S.
Определение. Пара целых чисел
В методе QS формируется множество аргументов х и чисел q(x), среди которых отыскиваются гладкие относительно факторной базы. Эти числа используются для построения соотношений, декларированных в цели метода. Ниже в примере приводится вариант такого формирования (таблица Д).
После формирования последовательности пар значений (х, q(x)) выполняем просеивание и находим значения хi, для которых
Если процесс формирования последовательности пар значений (х, q(x)) не является трудным для понимания, то процесс просеивания при чтении текста требует нашего внимания значительно больше. Раскроем его здесь в деталях. Пусть задан многочлен q(x) є Z[x]. Будем отыскивать все целые числа K в отрезке [-М, М] такие, что некоторые значения q(x) раскладываются в произведение простых чисел из заданного множества S.
Идея алгоритма просеивания множества чисел состоит в том, что если
Алгоритм QS
Все теоретические положения QS удобно оформить в виде шагов алгоритма:
1. Выбираются границы P и A порядка
2. Для аргумента
3. Для каждого нечетного простого числа p≤ P проверяем условие Лежандра (N/p)=1 и, если оно не выполняется, удаляем p из факторной базы. Однако, если мы разложим каждое значение q(x) по степеням простых чисел, то увидим, что некоторые числа из них не имеют множителей больше порога (в примере в разложении у 4-х чисел все факторы p≤11), а р = 5 не является
делителем ни одного из них, следовательно, факторную базу примера мы ограничим такими простыми числами S = (2,3,7,11):
4. Предполагая, что p такое нечетное простое число, что N –квадратичный вычет по модулю p; решаем сравнение
Берем значения β в порядке возрастания, пока не окажется, что уравнение не имеет решений x, сравнимых по модулю
Пусть
5. При том же значении p просматриваем список значений
Затем заменяем 2 на 3 у всех значений
6. Каждый раз, когда в пункте 5 ставим 1 или заменяем 1 на 2, 2 на 3 и т.д., делим соответствующее число
7. В столбце под p = 2 при N≢ 1(mod 8) просто ставим 1 против
8. Когда указанные действия будут проведены для всех простых чисел, не превосходящих P, отбросим все
Тогда получится таблица того же вида, что в примере метода факторизации Ферма, в которой столбец bi будет содержать все такие значения x из интервала
9. Оставшаяся часть процедуры в точности совпадает с процедурой из факторизации Ферма.
Пример. Будем применять последовательно положения теории алгоритма. Пусть задано составное число N =pq =112093, которое нужно разложить на множители. Следуя концепции квадратичного решета, извлекаем квадратный корень из N,
Далее в методе необходимо сформировать для i =1(1)А таблицу Д пар чисел
Таблица Д — Множество, содержащее В-гладкие числа (значения q(x)) с целыми аргументами

В этой таблице желательно иметь гладкие числа. Их надо выявить и оставить для дальнейшей обработки, а остальные можно просто удалить. Основной признак для удаления некоторого числа – наличие среди его делителей больших множителей (хотя бы одного), которые не вошли в факторную базу. В качестве границы гладкости примем В = 11.
Имеется возможность в процессе решения выбранное множество чисел изменять (уменьшать, увеличивать). В таблице Д среди значений q(х) нет полных квадратов. Теперь можно приступить к поиску чисел, которые обеспечат получение однородной системы линейных уравнений по модулю 2. Сама эта система нетривиальными решениями будет иметь переменные, произведения которых будут получать значения равные полному квадрату.
Просеивание
Рассмотрим в деталях как из множества значений
Уже сформирована 2-х строчная таблица Д пар чисел (х-верхняя строка, q(x) — нижняя) Все подряд значения q(x) (нижней строки таблицы Д) последовательно делят на все рj — простые числа (и их степени) из факторной базы S. Результаты деления вписывают в прежние позиции.
Те значения, которые не делятся на рj оставляют без изменений. Цель таких преобразований – не вычеркнуть полностью разделившиеся числа из таблицы, а получить в результате деления в их ячейках единичные значения, что соответствует В-гладким числам, т.е. полному разложению числа в таких позициях на степени простых из S. Также для этих ячеек выявляется аргумент х.
Дальше будем обрабатывать (делить) числа из строки таблицы Д

В результате получаем все четные числа, поделенные пополам в таблице Q, столбцы четных чисел чередуются с нечетными. Это закономерно. В исходной таблице четные чередовались с нечетными числами. Для любого целого d выполняется равенство

Изменившиеся числа выделены заливкой в ячейках, делим на (р = 2 β=2), т.е. еще раз.

Теперь все числа в таблице Q нечетные. Деление на простое р =2 и его степени 2×2=4 завершилось. Начинаем делить на следующее простое число из факторной базы (р =3, β = 1)

Если некоторое число разделилось на три, то каждое третье после него также делится на три. Таких цепочек чисел в таблице Q возникло две: 1-я цепочка начинается с первой ячейки; 2-я — с третьей.
Это следствие того, что квадратичное сравнение по модулю р имеет два решения (если вообще имеет решение). Делим на тройку всего три раза (р =3, β = 3), пока таблица при делении на нее не перестанет изменяться.

Следующее деление на 3 таблицу Q не меняет. Переходим к делению на (р =7,β = 1) т.е. к следующему числу факторной базы. Опять возникли 2 цепочки с началом в 4-й и в 5-й ячейках.

Еще два прохода с делителем (р = 7, β = 3) приводят к появлению первой единицы в таблице (предпоследнее число таблицы 49:7:7 =1).

Дальнейшее деление на 7 таблицу не меняет. Переходим к делению на (р = 11, β = 2) число из факторной базы, причем также делим двукратно и в результате получаем последнюю таблицу просеивания.

В ячейках таблицы (с аргументами х=335, 346, 347, 374) появились новые единицы. В позициях последней таблицы, содержащих единицы в исходном заполнении уже размещались 11-гладкие числа, но мы узнали об этом только после просеивания. Вот эти числа: 132, 7623, 8316, 27783.
Система линейных алгебраических уравнений и ее решение
Ни одно из значений таблицы Д вида
Выше показано, как эти четыре В-гладких числа найдены, без раскладывая всего списка чисел на множители. Соответствующая система линейных уравнений A×X = 0(mod 2) имеет матрицу коэффициентов по модулю 2 следующего вида:
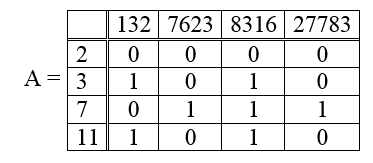
Верхняя строка матрицы — гладкие числа, левый столбец- факторная база. Следующим шагом нами получена нетривиальная линейная комбинация по модулю 2, в которой коэффициенты 0 и 1, и дающую в результате нулевой вектор. Для этого полученные результаты (В-гладкие числа) используют для формирования системы линейных алгебраических уравнений (СЛАУ), АХ≡0(mod2) решения которой приводят к окончательному результату-факторизации N.
Формируется А матрица СЛАУ, в которой векторы показателей гладких чисел записываются в столбцах, а вектор Х — определяемый неизвестный. Решением этой СЛАУ по модулю 2 получается вектор
В предшествующих обозначениях получены зависимости
X = П xi = 335 · 346 · 347=40220770, y = 91476.
Здесь X − y = 40220770 − 91476 = 40129294.
Находим НОД (X − y, N) = НОД (40129294, 112093) = 112093.
К сожалению, найденный делитель числа N = 112093 тривиален. Заметим, что и
НОД (X + y, N) = НОД (40312246, 112093) = 1 — тривиальный делитель.
Возьмем тогда другое решение системы АХ≡0(mod2), а именно решение (0101), получающееся при
Имеем X = Пxi = 346 · 374 = 129404, y = 14553. Находим
НОД (X − y, N) = НОД (114851, 112093) = 197.
Найден нетривиальный делитель 197 числа N = 112093. Теперь число N можно разложить на множители: N = 112093 = 569 · 197.
Заключение
В работе с определенной детальностью приводится изложение основных шагов и этапов алгоритма квадратичного решета (QS) для факторизации чисел ограниченной разрядности.
В отличие от подавляющего большинства публикаций, в которых практически не приводятся числовые примеры, в этой работе как раз такой пример дан с подробными комментариями. На этом примере удается продемонстрировать основные характерные действия излагаемого алгоритма.
Для своего времени алгоритм QS сыграл весьма положительную роль. Было показано, что «не боги горшки обжигают», но движения дальше не проявилось, так как последующие методы замкнулись на совершенствовании того же решета.
Список, использованной литературы
1. Агафонова И.В. Факторизация больших целых чисел и криптография 2006.
2. Брассар Ж. Современная криптология. М.: ПОЛИМЕД, 1999.
3. Василенко О. Н. Теоретико-числовые алгоритмы в криптографии. М.: МЦНМО, 2003
4. Нестеренко А.Ю. Теоретико-числовые алгоритмы в криптографии. Москва 2012
5. Rivest R. L., Shamir A., Adleman L. M. A method for obtaining digital signatures and public-key cryptosystems // Communications of the ACM. 1978. V. 21, P. 120–126.
6. The RSA Challenge Numbers // RSA Laboratories. www.rsasecurity.com/rsalabs/node.asp?id=2093
7. Стренг Г. Линейная алгебра и её применения. М.: Мир, 1980.
8. Смарт Н. Криптография. М.: Техносфера, 2005.
9. Shanks D. Five number-theoretic algorithms // Proceedings of the Second Manitoba Conference on Numerical Mathematics (Winnipeg), Utilitas Math. 1973. P. 51–70. Congressus Numerantium, No. VII.











