Комментарии 85
А линейка имеет ширину?
нарисовать по второй грани линейки параллельных линий до выхода за пределы пятна...
Ну если мы можем сделать циркуль операциями с линейкой - это тоже решение. Хотя возможно и не считающееся разрешенным. Ну или нанести шкалу.
Когда речь о задачах для ума, "не нужно" выглядит лишним) нельзя по правилам еще туда сюда. Наличие единичного отрезка выглядит запрещенным приемом, я согласен
неэлегантные
По меткому выражению одного из модераторов braingames, — "проявление смекалки в задачах на логику" )
Потому что в каждом комментарии пишете "так нельзя". Слишком много ограничений.
Все линейки которые я видел имели как миниум одну перпендикулярную сторону. По ней откладываем точку и продолжаем пендикуляр уже длинной стороной (если длины не хватает). Если линейка скорее похожа на кривой транспортир, то не прокатит.
</joke>
Если я не ошибаюсь, можно попытаться воспользоваться теоремой Дезарга
Потенциальное решение
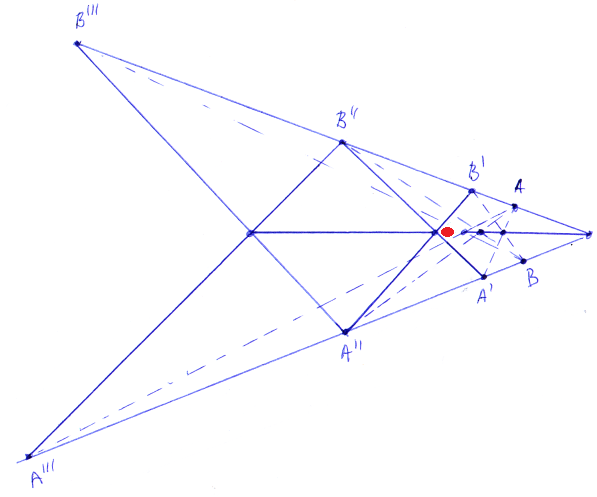
Будем строить два треугольника из теоремы. Концы отрезка возьмём за одну из пар вершин. Строим прямую, на которой будут пересекаться пары сторон треугольников. Отмечаем три точки на этой прямой, делаем это произвольно. Дальше строим стороны треугольников, проходящие через концы отрезка (по условию теоремы они должны пересекаться на только что построенной прямой с тремя выбранными точками). А вот третью пару сторон нужно строить так, чтобы прямые, их соединяющие, проходили мимо пятна. Поэтому на произвольность выбора трёх точек пересечения пар сторон накладывается ограничение - мы должны иметь возможность построить третьи стороны шире пятна. Это делать нужно «на глаз», так что это скользкий момент, не уверен, что здесь все честно. В общем, остаётся построить третью пару сторон, чтобы точка пересечения прямых, соединяющих концы этих сторон оказалась «по ту сторону пятна». Так мы построим одну точку с искомой прямой, немного «пошевелив» одну сторону из третьей пары, получим вторую точку.
Выбираем произвольные точки A и B, а так же три произвольные точки на исходном отрезке. Строим "проекции" точек A и B: A', A'', A''' и B', B'', B'''. Соединяем их попарно и точки пересечения будут искомыми концами отрезков.
Пока думал над задачей, возник такой вопрос: если подойти максимально формально, то есть, если единственная разрешённая операция построения — чертить прямую через выбранные две точки, то можно ли вообще гарантированно построить прямую, не проходящую через пятно?
То есть, проблема в следующем: выбрали одну точку, выбрали другую точку, пробуем провести прямую - и не можем, потому что она пересекает пятно. И так постоянно. По идее, при таком наборе разрешенных операций нет вариантов "выберем точку поближе" или "выберем точку в другой стороне".
1.Поставьте на плоскости 4 (или более) точек общего положения. Назовем их базисными.
2.Соедините базисные точки всевозможными прямыми.
3. Если пересечения прямых из пункта 2 — это какие-то базисные точки, то множество пункта 1 назовем «проекивносовершенным». Однако, вообще говоря, появятся новые точки. Примем их за новый базис и проделаем операции пункта 2 и 3.
4. Приведите пример, когда цикл построения (количество итераций) вообще говоря не прекратится ни на каком шаге и тем самым будет содержать счетное число шагов. Проверьте, что объединение точечных базисов всех шагов — это проективносовершенное множество (не важно, конечно итераций цикла или счетнобесконечно). Постарайтесь найти простое алгебраическое описание этого множества.
Решения лучше сразу в виде ссылок на GeoGebra публиковать, чтобы можно было подвигать точки и лучше понять, как эти решения работают.
Вот, например, моё решение: https://www.geogebra.org/calculator/tjmfmrkx
Вот очередное моё решение, надо посчитать будет количество линий.
www.geogebra.org/calculator/arajd4pn
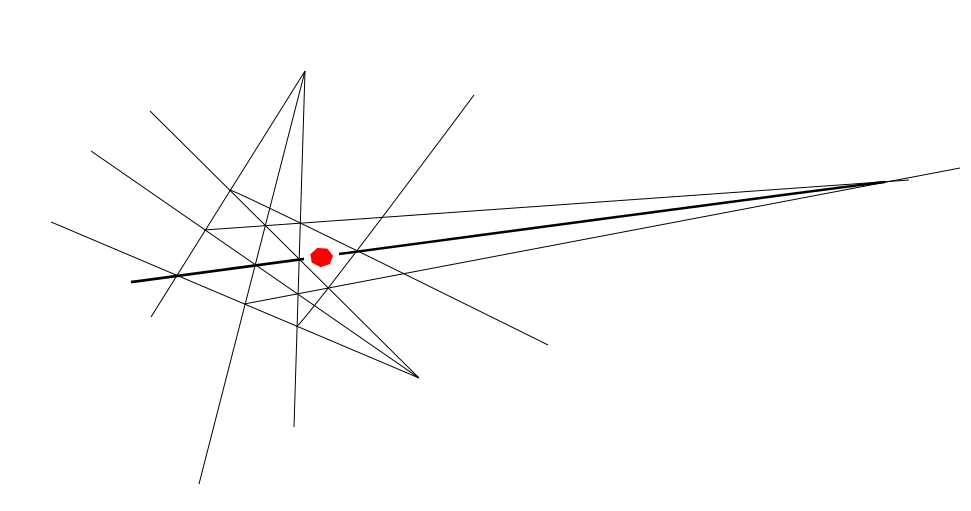
Построение при помощи циркуля и линейки, только… без циркуля