
Комментарии 16
Судя по объёму и сложности «статьи», нужно получить зачёт за публикацию?
Есть книги, из которых можно обо всем узнать и ничего не понять. (с) Гете.
излишне утрировано, вплоть до ошибочности.
В примере с ростом человека нигде не сказано, что считаем закономерностью. кусочно-линейную зависимость? полином? Что считаем ошибкой? индивидуальное отклонение? его квадрат? усредненный квадрат на наборе примероа?
Тема сама по себе интересная, я несколько новых мыслей придумал только из темы, но не надо так портить содержание.
Перепишите.
На Хабре уже не единожды, гораздо лучше и полнее рассмотрена эта тема.
Из уважения к аудитории, Вы могли хотя бы прочетсь эти статьи.
https://habr.com/ru/post/714988/
https://habr.com/ru/post/332198/
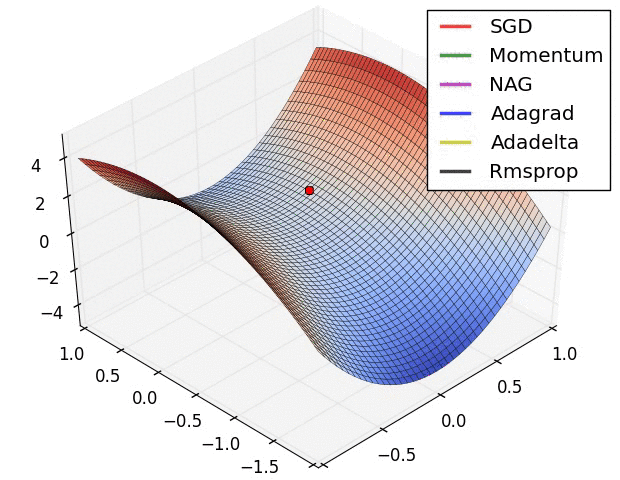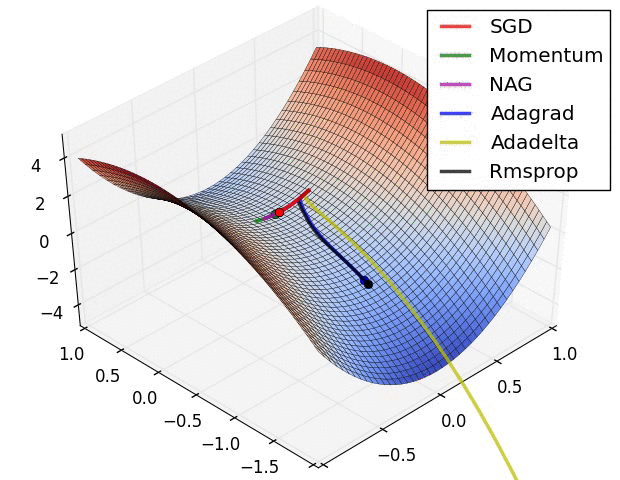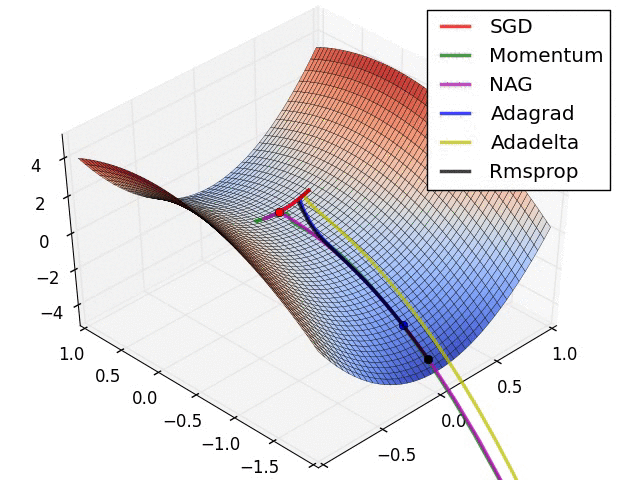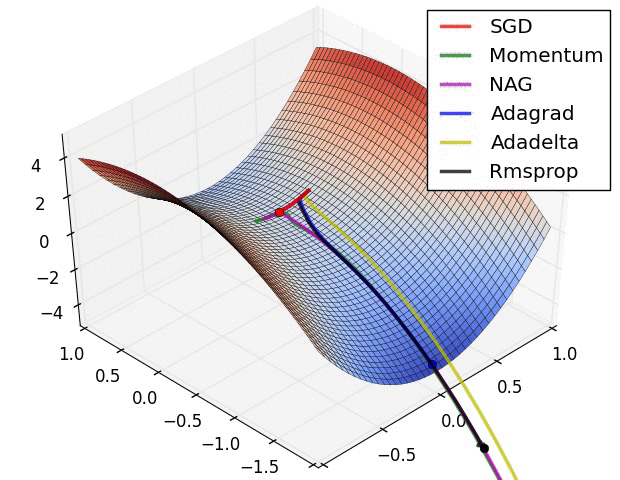
Обьясни, примерно так, градиентный спуск в ии это поиск самого быстрого лыжника.
Для поиска используется формула, где Л1 это лыжник, Л2 это лыжник два и т. Д.
П это путь.
С это скорость.
Таким образом: ...
Блин, почему рассматривается градиентный спуск именно в машинном обучении, ведь теряется его смысл. Изначально это численный медод нахождения экстремума, те по сути решение уравнения.И обычно смысл сводится к тому, что шаг приближения делается в направлении максимального приращения ( убывания функции), для чего используют первую производную. Причем чем более "крутая" функция, тем быстрее сходимость и обратно чем более пологая, тем дольше сходимость.
вот, с этого бы начать, на простых примерах, потом обобщить до многомерного случая, показать всякие необычные случаи, и только потом рассказать, что в NN тоже применимо, и подробно показать-рассказать, как.
Нет, градиент это локальное направление наибыстрейшего убывания/возрастания функции. Градиентный спуск это итеративный процесс движения вдоль градиента. Если функция выпуклая то мы более менее гарантированно попадаем в глобальный оптимум.
Формально приравнивая градиент нулю, мы находим локальные "ямы". Проблема в том, что если функция достаточно сложная, то решение "обратной задачи" нахождения точек где градиент равен нулю, может быть сопоставимо по сложности или сложнее чем исходная задача оптимизации, да и таких "ям" может быть счетная бесконечность.
То что делают в школе приравнивая градиент нулю с ростом размерности и сложности, становится все менее и менее применимо на практике.
Блин, почему рассматривается градиентный спуск именно в машинном обучении, ведь теряется его смысл.
Ну почему же теряется? Внутри обучающейся сетки то же самое и происходит. Наоборот, считаю, при изучении машинного обучения надо это знать. Чтобы не думать, что там внутре какое-то колдунство творится.
Машинное обучение появилось сильно позже численных методов нахождения экстремумов. Можете вспомнить метод Ньютона ( частный метод градиентного спуска), половинного деления, метод Метод Рунге — Кутты это прям базовы, что на ум пришли. И все изучают примерно от простого к сложному.
Я про поиск оптимума в пространстве синоптических весов нейронов. Он же и идёт такими способами, например градиентным спуском по функции потерь от вектора весов. По крайней мере, в тех простейших нейросетях, которые я знаю)
извините за сарказм, но изначально было Градиентный спуск простыми словами ...
а вы тут
поиск оптимума в пространстве синоптических весов нейронов
Это ж никак ни помогает понять. Я бы смотрел на градиентный спуск, но начинал бы с метода Ньютона и только потом бы усложнял бы на ваше машинное обуччение
Градиентный спуск простыми словами