kkalmutskiy 5 сен 2023 в 08:11

Строим удобные автомобильные маршруты

Средний

8 мин

11K

Блог компании 2ГИСАлгоритмы*Геоинформационные сервисы*Big Data*Машинное обучение*

Хороший автомобильный маршрут из точки А в точку Б должен, с одной стороны, быть кратчайшим, а с другой — удобным для водителя. Как правильно вычислить время в пути мы уже рассказали, теперь — об удобстве маршрутов: что это такое, как его измерить и как мы его повышали.

Базовый алгоритм построения маршрутов

Дороги в городе представляются в виде дорожного графа, вершины которого — ключевые точки дорожной сети (перекрёстки, места изгибов и так далее), а рёбра — дорожные сегменты. Таким образом, считаем, что маршрут из А в Б — это путь в дорожном графе, начинающийся в вершине А и заканчивающийся в вершине Б.

Чтобы найти путь минимальной стоимости, в дорожном графе используется алгоритм А*: он вычислительно эффективный и находит оптимальный путь относительно выбранной функции стоимости.

Примерно так выглядит дорожный граф, чёрным выделено отдельное ребро

В качестве функции стоимости удобно использовать время в пути (ETA): тогда найденный маршрут будет кратчайшим среди всех возможных. В простейшем случае время в пути складывается из двух факторов: времени проезда по рёбрам графа и дополнительного времени на совершение маневров при переходе из одной вершины графа в другую.

Про то, как мы вычисляем время в пути по ребру, можно прочитать в этой статье.

Что не так с алгоритмом

Проблема в выбранной функции стоимости — при построении маршрута мы не учитываем ничего, кроме времени в пути. Найденный маршрут может быть крайне неудобен, и пользователь не поедет по нему, несмотря на его оптимальность. Поэтому хочется добавить в функцию стоимости некоторые бизнес-правила, чтобы отбрасывать плохие маршруты ещё на этапе построения, а не на этапе пост-фильтрации.

Маршрут слева — быстрее того, что справа, но проходит через дворы

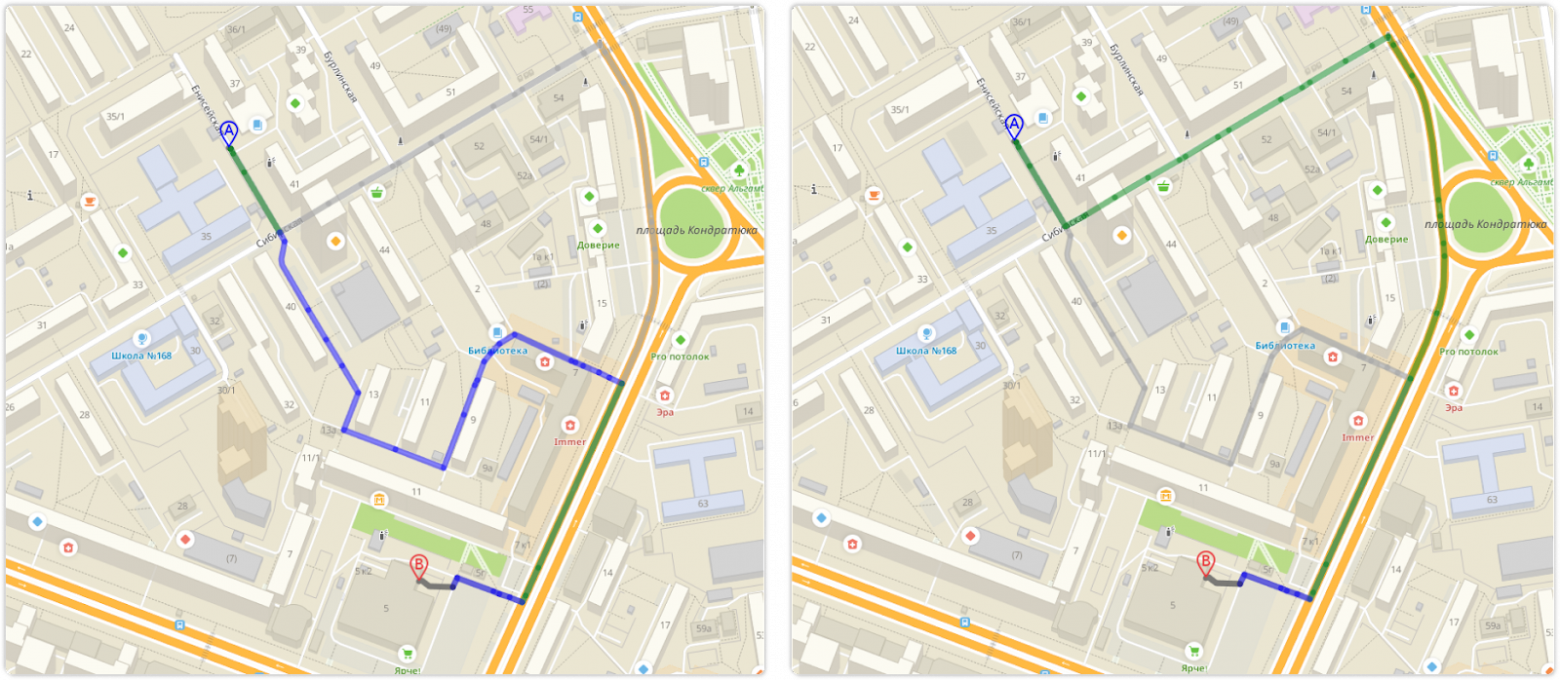
Бизнес-логику реализуем с помощью штрафов — это дополнительное время на различные вариации построения. Завели на кольцо? Получаем за это 15 секунд штрафа. Пытаемся заехать на разбитую дорогу? Этот маленький манёвр будет стоить нам 5 минут. Увидели шлагбаум? Либо едем в объезд, либо плюсуем еще 60 минут.

Штрафы работают как «мягкие» запреты на проезд в выбранном направлении: если нет альтернативы с меньшей стоимостью, то маршрут через это направление всё равно построится. Для «жесткого» запрета существуют перекрытия — временное удаление рёбер из дорожного графа.

В такой постановке удобно превратить время на совершение манёвров в штрафы за манёвры. Логика в определении размера штрафа может быть такой: сколько пользователь готов проехать лишнего времени по прямой, чтобы не совершать дополнительный манёвр? Так, может оказаться, что реальное время разворота всего 5 секунд, тогда как «психологическое» время — целых 60 секунд. Чем больше штрафы за повороты выберем, тем более прямыми будут получаться маршруты.

Важно понимать, что теперь полученная функция стоимости, хоть и представляется в секундах для удобства, не является временем в пути. И после построения маршрута итоговое время нужно вычислять отдельно. В итоге получаем такую функцию стоимости:

$\begin{equation*} F_{cost}(route) = \sum_{i=1}^n t(edge_i) + \sum_{i=1}^m c^*(turn_i) + \sum_{i=1}^k r_i^* \end{equation*}$

С помощью штрафов мы делаем маршруты немного длиннее, но при этом значительно более удобными. Удобными в том смысле, в котором его видим мы как разработчики. А что насчёт пользователей?

It’s Big Datain’ Time

Пользовательские предпочтения правилами описать уже гораздо сложнее. Например, на отказ от поездки по построенному маршруту может влиять множество факторов, о которых мы заранее не знаем или которые трудно оценить:

Дороги плохого качества: плохое покрытие, множество ям, отсутствующая разметка и так далее;
Непривычный маршрут: удобнее ездить по тем дорогам, по которым уже когда-то проезжал, поскольку знаешь, чего ожидать;
Сложные повороты или перекрёстки, которых хочется избежать в маршруте;
Личные предпочтения: какая-то альтернативная дорога просто может нравиться больше, даже если она не кратчайшая;
Системные ошибки в определении скоростей на некоторых дорогах (например, из-за недостатка данных), из-за чего построенный маршрут на самом деле не будет оптимальным.

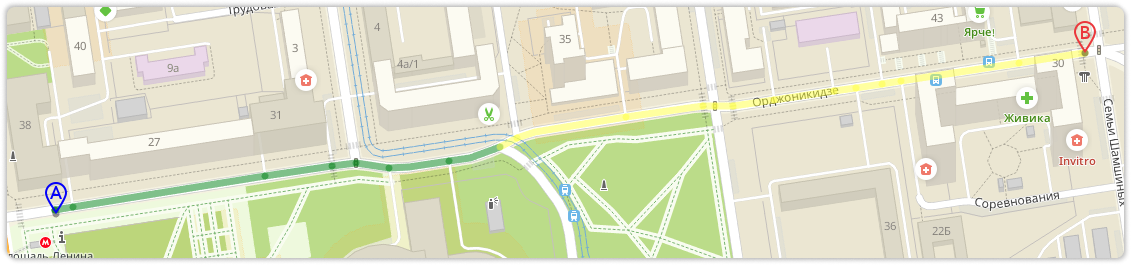
К счастью, перечисленные проблемы обычно относятся только к некоторому участку маршрута, а не ко всему маршруту в целом. Поэтому пользователь во время поездки может съехать на дорогу, которая ему больше нравится (навигатор перестроит маршрут после съезда), вместо того, чтобы отказаться от поездки по навигатору вообще.

Сплошная линия — первый построенный маршрут, точки — то, как ехал пользователь на самом деле

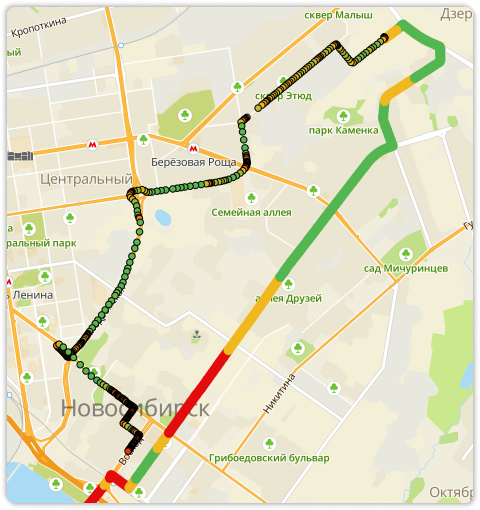
Для каждой состоявшейся поездки мы сохраняем маршрут: набор рёбер, которые мы предложили пользователю, и набор GPS-точек, полученные от пользователя во время поездки. С помощью небольшой магии мы превращаем набор GPS-точек в трек — набор рёбер, по которым ехал пользователь:

Таких пар «маршрут-трек» у нас очень много, значит, самое время открыть Jupyter Notebook и придумать, как извлечь из этих данных что-то полезное.

Вероятность проезда по ребру

Во время построения маршрута алгоритм перебирает десятки тысяч рёбер, чтобы найти оптимальный путь. Поэтому какие-то тяжёлые модели не получится добавить без значительной просадки перфоманса. Нужно что-то простое и эффективное — желательно то, что можно вычислить заранее, до построения маршрута.

И это «что-то» нашлось. Встречайте — вероятность проезда по рёбрам графа. Её расчёт выглядит примерно так: для каждого ребра и пары «маршрут-трек» сначала находим следующее число:

$I_{route}(edge) = \left\{ \begin{array}{ll} 1 & \text{если } \text{edge} \text{ есть в } \text{route} \text{ и есть в } \text{track} \\ 0 &\text{если } \text{edge} \text{ есть в } \text{route} \text{ и нет в } \text{track} \\ \text{null} & \text{если } \text{edge} \text{ нет в } \text{route} \end{array} \right.$

edge	есть в track	нет в track
есть в route	1	0
нет в route	null	null

Усредняем массив полученных значений, посчитанных по всем парам «маршрут-трек» (null игнорируем в расчете среднего), и получаем вероятность проезда по ребру с учётом того, что через него построен маршрут:

$p_{edge} = \frac{\sum_{i=1}^n I_{route_i}(edge)}{\sum_{i=1}^n[ I_{route_i}(edge) \neq null]}$

Есть одна проблема: мы ограничены теми рёбрами, через которые маршруты строятся, и для некоторых ребер никакая вероятность не посчитается. Плюс нам хотелось бы поднять эту вероятность для тех рёбер, которых нет в маршрутах, но которые часто встречаются в треках. Для этого немного модифицируем формулу:

$I_{route}(edge) = \left\{ \begin{array}{ll} 1 & \text{если } \text{edge} \text{ есть в } \text{track} \\ 0 &\text{если } \text{edge} \text{ есть в } \text{route} \text{ и нет в } \text{track} \\ \text{null} & \text{если } \text{edge} \text{ нет в } \text{route} \text{ и нет в } \text{track} \end{array} \right.$

edge	есть в track	нет в track
есть в route	1	0
нет в route	1	null

Получаем вот такие карты вероятностей проезда по рёбрам, которые можно анализировать на предмет того, где и почему встречаются «плохие» дороги с низким значением вероятности проезда:

— Вы фиксите плохих рёбров? — Нет, просто показываем — Красивое... — — Вы фиксите плохих рёбров?
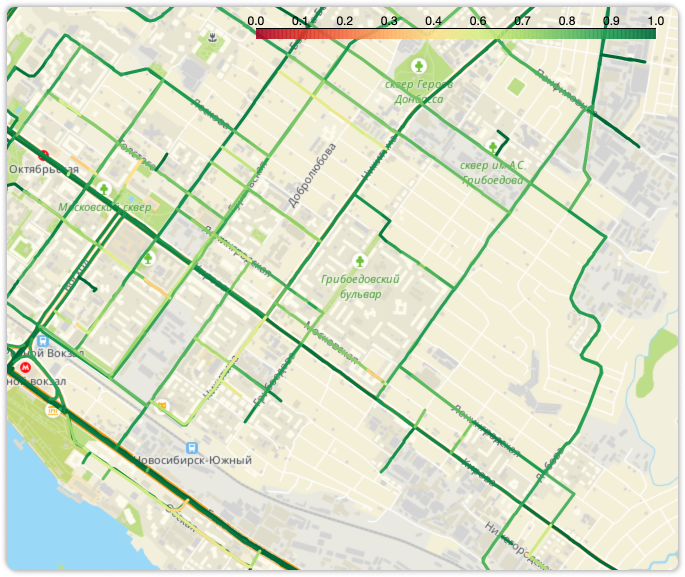
— Нет, просто показываем
— Красивое...

Итак, мы научились считать некоторую характеристику, которая приблизительно показывает, насколько конкретное ребро нравится или не нравится пользователям. Давайте теперь использовать эту характеристику при определении «психологического» времени проезда по ребру, чтобы штрафовать рёбра за низкую вероятность проезда, например, вот так:

$\begin{equation*} F_{cost}(route) = \sum_{i=1}^n \frac{t(edge_i)}{f(p_{edge_i})} + \sum_{i=1}^m c^*(turn_i) + \sum_{i=1}^k r_i^* \end{equation*}$

В качестве весовой функции может выступать любая неубывающая функция. Забегая вперёд, после серии экспериментов лучше всего себя показал вот такой зверь:

Идея есть, осталось её реализовать и посмотреть на результаты. Закрываем Jupyter Notebook и идём делать сервис.

Проблемы сходимости

Предвкушая невероятный успех от введения вероятностей, мы локально собрали первый прототип, начали строить маршруты и, применив метод пристального взгляда, поняли, что получается что-то не то. Новые маршруты слишком сильно отличались от старых, причем не всегда в лучшую сторону. Начали игнорировать какие-то очевидные короткие проезды, где-то, наоборот, стали избегать магистрали и предпочитать непонятные дороги.

Это происходило по двум причинам:

Рёбра графа сильно связаны между собой: изменение вероятности проезда на одном конкретном ребре повлечет за собой изменение вероятностей проезда на множестве других ребер графа;

Вероятность проезда по ребру — апостериорная: она зависит от алгоритма построения. Когда мы меняем алгоритм построения, автоматически меняются вероятности проезда по ребрам.

Получаем замкнутый круг:

Всё указывает на то, что веса нужно подбирать итеративно до сходимости. Чтобы понять, что в нашем случае будет сходимостью, внимательно посмотрим на возможные значения вероятностей проезда.

Низкие и средние значения: пользователи редко проезжают по этому ребру в маршруте.
Вывод: мы слишком часто строим маршруты через это ребро. Нужно уменьшить вес при построении.
Очень высокие значения: пользователи всегда проезжают по этому ребру в маршруте.
Вывод: либо это безальтернативный проезд, либо мы слишком редко строим маршруты через это ребро. Нужно увеличить вес при построении.
Высокие значения: пользователи часто проезжают по этому ребру в маршруте, но иногда выбирают альтернативные проезды.
Вывод: ребро имеет оптимальную вероятность проезда. Вес при построении менять не нужно.

В идеале мы хотим, чтобы все рёбра имели высокое значение вероятности проезда, именно это и будем считать критерием сходимости. Каким методом оптимизации мы пользуемся? Конечно же, градиентным спуском! Будем итеративно двигать веса в нужную сторону тем сильнее, чем больше текущая вероятность отличается от оптимальной.

Чтобы помочь алгоритму быстрее сойтись к оптимуму, инициализируем веса не единицами, а в соответствии с типом дороги: например, магистралям поставим начальные значения повыше, а дорогам минимальной значимости — пониже. Кстати, такая начальная инициализация сама по себе сильно улучшает базовый алгоритм, даже без добавления вероятностей проезда.

Описываем удобство в цифрах

Прежде чем выкатывать изменения на прод, надо ответить на вопрос: как мы поймем, что стало лучше и удобнее? Есть два способа оценки:

Явный отклик: оценка маршрута в конце поездки, тапы на кнопку «Я знаю маршрут лучше»;
Неявный отклик: качество построенного маршрута на основе сопоставления маршрута и трека.

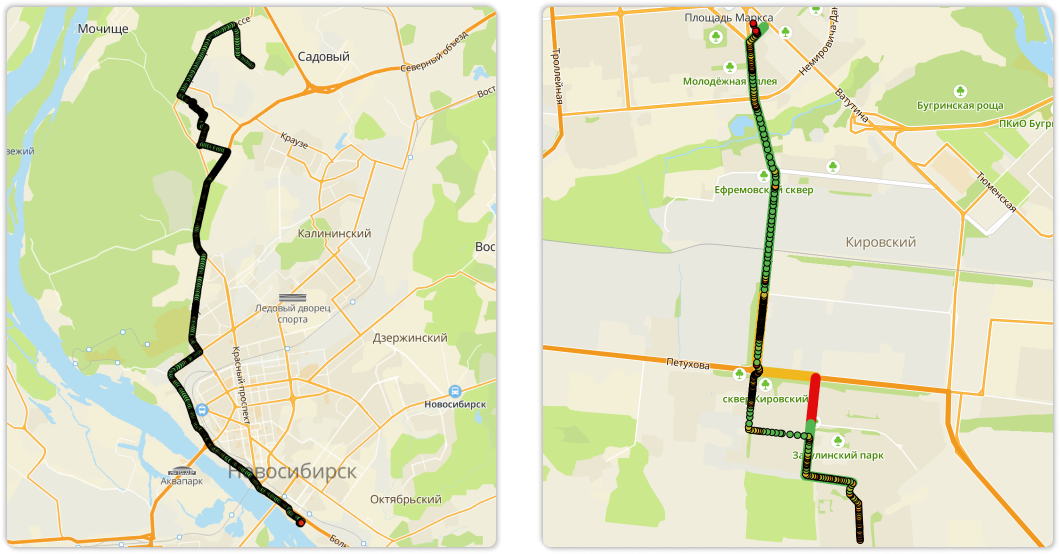
Сначала про явный отклик: итоговая оценка маршрута пользователем зависит не только и не столько от предложенной геометрии маршрута. Это будет мешать корректному анализу. Статистики по «Я знаю маршрут лучше» слишком мало, чтобы делать по ней какие-то далеко идущие выводы.

Поэтому основные метрики основаны на неявном отклике — его как раз очень много. В итоге мы остановились на трёх самых информативных метриках:

Процент времени, которое пользователь провёл на маршруте.
Процент длины маршрута, покрытого треком.
Количество перестроений маршрута во время поездки.

Предполагаем, что с удобного маршрута редко придётся съезжать, а если и придётся, то пользователь всё равно вернётся на изначальный маршрут через некоторое время.

Изменения начали проверять с помощью A/B-тестирования: на одном контуре использовали веса при построении маршрутов, на другом — не использовали. В течении нескольких итераций алгоритма метрики качества маршрутов росли, что сигнализировало о том, что алгоритм сходится к некоторому оптимуму.

Новый алгоритм (справа) чаще ведёт на главные дороги города, несмотря на пробки. Забавный факт: время в пути для обоих маршрутов одинаковое.

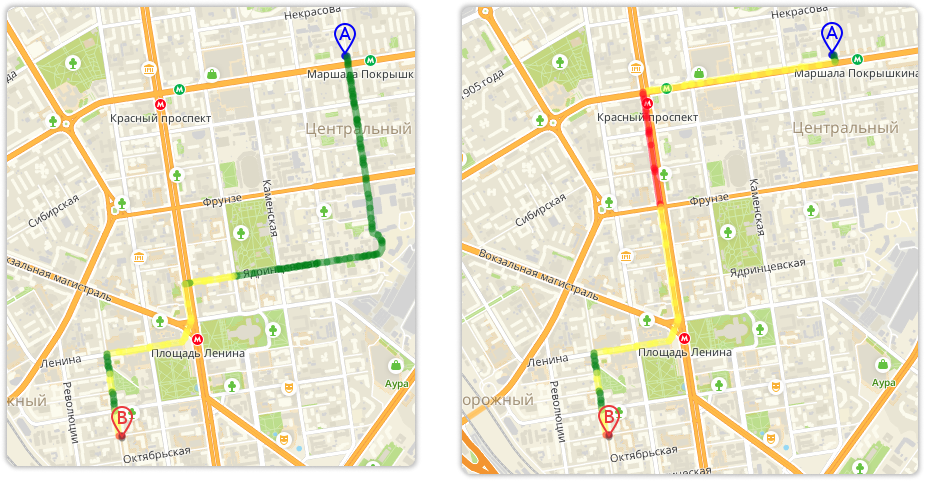
Когда убедились, что нет никаких серьёзных ошибок в построении, полностью выкатили изменения в тех городах, где достаточно данных для достоверного расчёта вероятностей. Чтобы учитывать изменения дорожного графа, мы не останавливаем итерации алгоритма и постоянно обновляем веса.

Вероятность совершения поворота

Если внимательно посмотреть на итоговую функцию стоимости при построении маршрута, может появиться непреодолимое желание добавить веса и на слагаемые во второй сумме:

$\begin{equation*} F_{cost}(route) = \sum_{i=1}^n \frac{t(edge_i)}{f_e(p_{edge_i})} + \sum_{i=1}^m \frac{c^*(turn_i)}{f_t(p_{turn_i})} + \sum_{i=1}^k r_i^* \end{equation*}$

Именно это мы и в итоге и сделали. Будем считать, что поворот — это пара рёбер в которой при переходе из в меняется направление движения. Таким образом, прямые проезды из одного сегмента дороги в другой мы не считаем поворотами.

На этом участке дороги несколько рёбер, но поворотов нет

Если посчитать характеристику, которая показывает вероятность проезда по паре ребер (с учётом, что она встречается в маршруте), то получим фактически то же самое, что уже посчитали до этого. Поэтому сделаем иначе — для каждого поворота в маршруте получим следующее число:

$I_{route}(edge_1, edge_2) = \left\{ \begin{array}{ll} 1 & \text{если } (edge_1, edge_2) \text{ есть в } \text{route} \\ & \text{и } (edge_1, edge_2) \text{ есть в } \text{track} \\ 0 & \text{если } (edge_1, edge_2) \text{ есть в } \text{route} \text{, } \\ & edge_1 \text{есть в } \text{track} \text{ и } edge_2 \text{ нет в } \text{track}\\ \text{null} & \text{иначе} \end{array} \right.$

Вероятность совершения манёвра аналогично получается в результате усреднения вычисленных значений по всем парам «маршрут-трек».

$p_{turn} = p_{(edge_1, edge_2)} = \frac{\sum_{i=1}^n I_{route_i}(edge_1, edge_2)}{\sum_{i=1}^n[ I_{route_i}(edge_1, edge_2) \neq null]}$

Эта характеристика показывает, какова вероятность совершить поворот, если он был построен в маршруте и у пользователя была реальная возможность проехать по нему.

Сделали такие же красивые карты для вероятностей поворотов

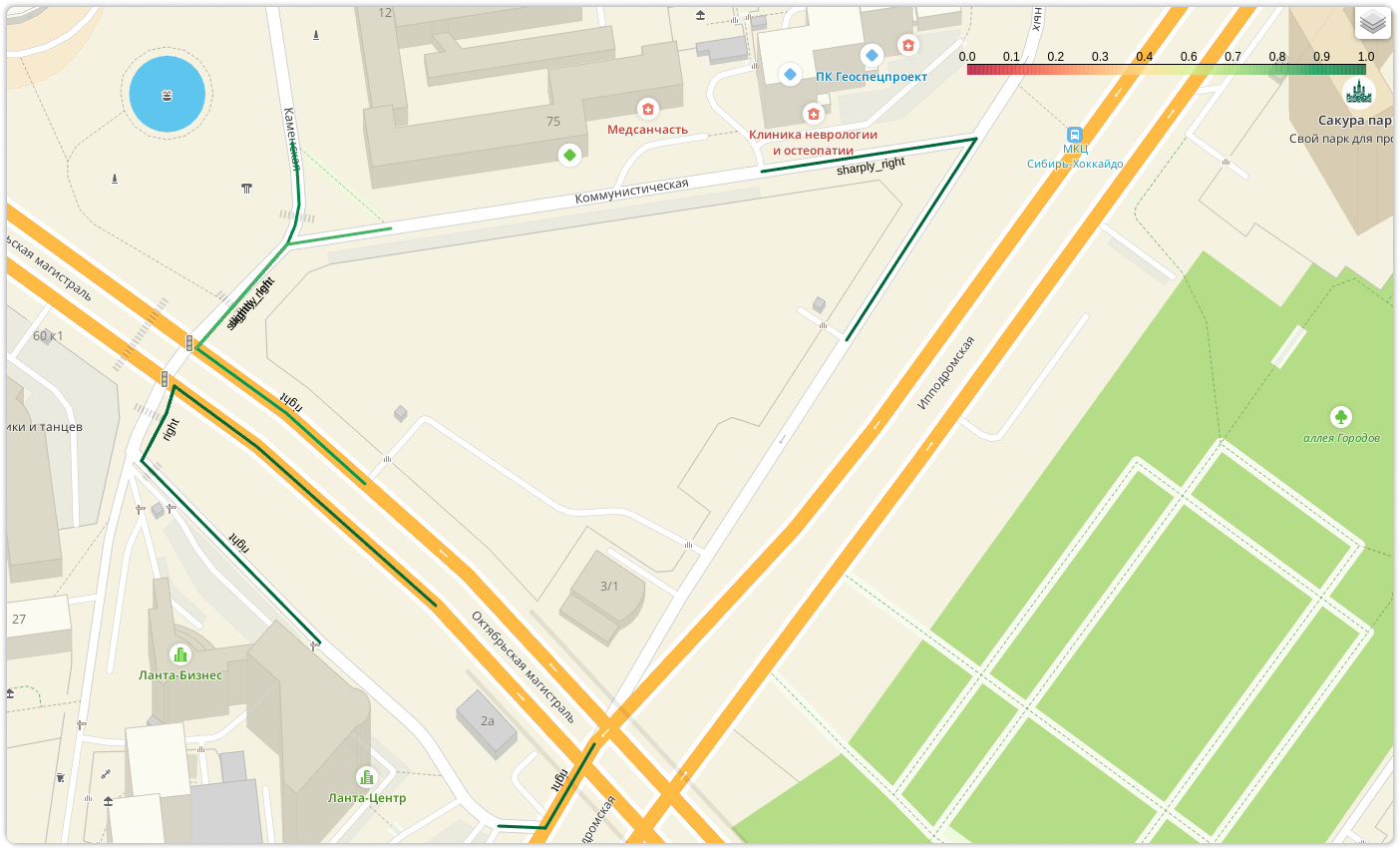
Дальнейшая судьба у этих вероятностей такая же, как у их старшего брата: итеративное обновление до сходимости, А/В-тестирование, замер метрик и попадание на прод. Только в этот раз всё прошло намного быстрее и более гладко, правда, и влияние на метрики было менее заметным. Главный профит от их добавления — это избегание при построении каких-то совсем неудобных поворотов, в особенности, разворотов.

Финал

Были также попытки перенести всё это на пешеходную маршрутизацию, но в ней идея использования вероятностей в таком виде не зашла и требует переосмысления. Сказывается недостаток данных и особенности функции стоимости, ведь для пешеходов мы, к сожалению, не считаем пробки, хотя где-то это было бы даже полезно.

В автомобильной маршрутизации мы достигли изначально поставленной цели: строить не только самые быстрые, но ещё и самые удобные для среднестатистического пользователя маршруты. Конечно, кроме вероятностей проезда было сделано ещё много всего для улучшения качества маршрутов: различные дополнительные штрафы при построении, модификация подбора и сортировки альтернативных маршрутов, ограничения на возможную геометрию… Но в первую очередь хотелось рассказать про самый интересный и «живой» компонент во всей схеме. Пока вы читали эту статью, возможно, он уже обновился :)

Теги:

Хабы: