Теоретическая информатика — одно из направлений обучения на кафедре Математических и информационные технологий Академического университета. Нас часто спрашивают, чем занимается теоретическая информатика. Теоретическая информатика — активно развивающееся научное направление, включающее в себя как фундаментальные области: алгоритмы, сложность вычислений, криптография, теория информации, теория кодирования, алгоритмическая теория игр, так и более прикладные: искусственный интеллект, машинное обучение, семантика языков программирования, верификация, автоматическое доказательство теорем и многое другое. Эту статью мы посвятим обзору лишь небольшого сюжета, а именно расскажем о необычных подходах к понятию доказательства, которые рассматривает теоретическая информатика.

Чтобы объяснить, о какого рода доказательствах пойдет речь, рассмотрим пример: есть компьютерная программа, авторы которой утверждают, что программа делает что-то определенное (конкретные примеры будут чуть позже). Программу можно запустить и получить ответ. А как можно удостовериться, что программа делает то, что должна делать? Хорошо бы, если кроме ответа программа выдавала бы доказательство того, что этот ответ правильный.
Рассмотрим более конкретный пример: мы хотим иметь программу, которая в двудольном графе находит паросочетание максимального размера вместе с доказательством его максимальности.
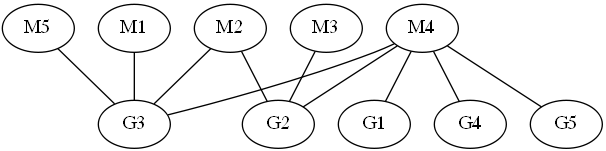
Напомним, что граф называется двудольным, если его вершины можно покрасить в два цвета так, что ребра графа соединяют вершины разных цветов. Паросочетанием в графе называется такое множество ребер, что никакие два из них не имеют общего конца. Множество вершин графа называется покрывающим, если каждое ребро графа имеет как минимум один конец в этом множестве. Теорема Кенига гласит, что в двудольном графе размер максимального паросочетания совпадает с размером минимального покрывающего множества. Таким образом, чтобы доказать, что паросочетание является максимальным, можно предъявить, покрывающее множество, размер которого совпадает с размером данного паросочетания. Действительно, это покрывающее множество будет минимальным, поскольку каждое покрывающее множество обязано покрыть хотя бы один конец каждого ребра этого паросочетания. Например, в графе на рисунке паросочетание (M1, G3), (M2, G2), (M4,G1) будет максимальным, поскольку есть покрывающее множество размера 3, которое состоит из G2, G3 и M4. Отметим, что проверить такое доказательство гораздо проще, чем вычислять максимальное паросочетание: достаточно проверить, что размер паросочетания совпадает с размером покрывающего множества и проверить, что все ребра покрыты.
Рассмотрим еще один пример, допустим нам нужна программа, которая проверяет систему нестрогих линейных неравенств с рациональными коэффициентами на совместность (напомним, что система неравенств называется совместной, если можно подобрать такие значения переменных, что все неравенства выполняются).

Как можно доказать правильность результата? Если система совместна, то доказательством совместности может стать решение этой системы (нетрудно доказать, что если у такой системы есть решение, то есть и рациональное решение, т.е. его можно записать). А как доказать, что система несовместна? Оказывается, что это сделать можно с помощью леммы Фаркаша, которая утверждает, что если система нестрогих линейных неравенств несовместна, то можно сложить эти неравенства с неотрицательными коэффициентами и получить противоречивое неравенство 0≥1. Например, система на рисунке несовместна, и если сложить первое уравнение с коэффициентом 1, второе с коэффициентом 2, а третье с коэффициентом 1, то получится 0≥1. Доказательством несовместности будет как раз набор неотрицательных коэффициентов.
В этой статье мы поговорим о том, нужны ли доказательства, или проверка доказательства всегда не проще, чем самостоятельное решение задачи. (В примере про максимальное паросочетание мы не доказали, что не существует алгоритма, решающего задачу за то же время, сколько занимает проверка доказательства.) Если мы не ограничиваем размер доказательства, то окажется, что доказательства нужны, а если будем требовать, чтобы доказательства были короткими, то вопрос о нужности доказательств эквивалентен важнейшему открытому вопросу о равенстве классов P и NP. Потом мы поговорим об интерактивных доказательствах (доказательства в диалоге). Обсудим криптографические доказательства, которые не разглашают лишнюю информацию, кроме верности доказываемого утверждения. И закончим обсуждением вероятностно проверяемых доказательств и знаменитой PCP-теоремы, которая используется для доказательства трудности приближения оптимизационных задач.
В этой статье мы не будем касаться автоматического доказательства теорем и доказательства корректности программ, хотя эти темы тоже достаточно интересны.
Языком называется множество строк над некоторым конечным алфавитом. В теоретической информатике обычно рассматривают доказательства утверждений вида x∈L, где L — язык, а x — некоторая строка. Утверждения такого вида обобщают математические теоремы, поскольку любая математическая теорема гласит, что утверждение, записанное на формальном языке, принадлежит множеству истинных утверждений.
Системой доказательств для языка L называется алгоритм A(x,w), который получает на вход две строки: x и w и проверяет, что строка w является доказательством принадлежности x∈L. От системы доказательств требуют два свойства: корректность и полноту. Корректность утверждает, что если для некоторых строк x и w алгоритм A(x,w) выдает 1, то x∈L. Полнота утверждает, что для каждого x∈L существует такая строка w, что алгоритм A(x,w) выдает 1.
Языки, для которых существуют системы доказательств, называются перечислимыми языками. Если вы сталкивались с другим определением перечислимого языка, то в качестве упражнения, докажите их эквивалентность.
Язык L называется разрешимым, если существует такой алгоритм B, что при x∈L алгоритм B(x) выдает 1, а при x∉L выдает 0. Любой разрешимый язык имеет систему доказательств, в которой доказательство пустое. Естественный вопрос, обязательно ли, что для любого языка, для которого есть система доказательств, найдется и разрешающий алгоритм. Ответ на этот вопрос известен, существуют языки, для которых есть системы доказательств, но для которых нет разрешающего алгоритма. Придумать какой-то пример такого языка несложно, сложнее придумать естественный пример. Рассмотрим язык, который состоит из многочленов с целыми коэффициентами от многих переменных, которые обращаются в ноль хотя бы при каком-то целочисленном значении переменных. Система доказательств для такого языка строится просто: доказательством будет целочисленное значение переменных, в которых многочлен обращается в ноль. DPRM-теорема (названа по авторам: Дэвис, Путнам, Робинсон и Матияесевич) утверждает, что этот язык не является разрешимым, т.е. не существует алгоритма, который проверит, обращается ли многочлен в ноль в целых точках. Последний шаг в доказательстве этой теоремы принадлежит академику Ю. В. Матиясевичу и эта теорема дает отрицательный ответ на 10-ю проблему Гильберта.
Пока мы не накладывали никаких ограничений на алгоритм, который проверяет доказательство и на размер доказательства. Будет ли полезным доказательство корректности результата некоторой программы, если время, которое потребуется на проверку доказательства больше, чем на выполнения самой программы? Кажется, что такие доказательства бессмысленны, поэтому будем требовать, чтобы алгоритм A(x,w) в определении системы доказательств работал бы полиномиальное от длины строки x и от длины доказательства w время, такие системы доказательств будем называть эффективными.

Будем говорить, что язык L принадлежит классу NP, если для него есть эффективная система доказательств и полином p, что для любого x∈L существует доказательство принадлежности x∈L длины не большей, чем p(|x|). Язык L принадлежит классу P, если существует полиномиальный по времени алгоритм, который проверяет принадлежность входной строки языку L. Класс P содержится в классе NP, поскольку для каждого языка L из P, алгоритм, проверяющий принадлежность L, сам и будет системой доказательств, если считать, что он игнорирует доказательство. На данный момент неизвестно, существуют ли языки из класса NP, которые не принадлежат классу P. Вопрос о равенстве классов P и NP входит в список семи задач тысячелетия, составленный институтом Клэя; за решение этой задачи объявлен приз в миллион долларов. Многие слышали про список задач тысячелетия в связи с доказательством гипотезы Пуанкаре Г. Я. Перельманом. Большинство специалистов полагают, что классы P и NP не совпадают.
Рассмотрим примеры языков из класса NP:
До сих пор доказательства, которые мы рассматривали, были очень похожими на привычные нами, а именно, доказательство — это некоторый текст, который, хотя и непонятно как придумывать, но легко проверить, есть алгоритм, который проверяет корректность доказательства. Т.е., чтобы придумать доказательство нужно иметь какие-то специальные способности, а проверить доказательство может каждый. На самом деле совсем не все доказательства современной математики обладают этим свойством. Во-первых, доказательства не пишут на удобном для автоматической проверки формальном языке, а во-вторых, чтобы понять доказательство в некоторых областях, нужно несколько лет потратить на изучение этой области.
В математических кружках для школьников часто практикуется такой формат занятий: детям выдается набор задач, когда ребенок считает, что он решил задачу, то он устно рассказывает решение преподавателю. И происходит диалог между преподавателем и учеником, который либо убеждает преподавателя в том, что задача решена, либо не убеждает.
Рассмотрим пример интерактивного доказательства: есть программа, которая решает задачу изоморфизма графов. В случае, когда графы изоморфны, программа может доказать правильность своего ответа, выдав перестановку, задающую изоморфизм. Покажем, как можно в диалоге доказать, что графы неизоморфны. Пусть пользователь спросил программу, изоморфны ли графы G0 и G1 и получил ответ, что они неизоморфны. После этого пользователь бросает монетку (выбирает случайный элемент i из множества {0,1}) и выбирает случайную перестановку n-элементного множества (при этом все перестановки считаются равновероятными) σ. И спрашивает программу, изоморфны ли графы G0, σ (Gi). Если i=0, то от программы ожидается ответ, что графы изоморфны, а если i=1, то от программы ожидается, что графы неизоморфны. Если графы G0 и G1 действительно были неизоморфны, то программа без труда даст правильный ответ на этот вопрос. А если же G0 и G1 были изоморфны, то граф σ (Gi) с равной вероятностью может быть как перестановкой G0, так и перестановкой G1, следовательно программа выдаст ожидаемый ответ с вероятностью не больше, чем 1/2. Вероятность ошибки можно уменьшить, повторив алгоритм n раз и решить, что алгоритм верно работает, если в каждом из n запусков был дан верный ответ; вероятность ошибки в таком случае не превосходит 1/2n.
В рассмотренном только что примере доказательство — это диалог между доказывающим (программой) и проверяющим (пользователем), при этом доказывающий может быть устроен очень сложно, а проверяющий может делать только простые вещи (производить полиномиальные по времени вычисления). Если элемент x∈L, то доказывающий должен с вероятностью 1 убедить в этом проверяющего, а если x∉L, то проверяющий должен принять такое доказательство с вероятностью не больше, чем 1/10. Теорема Шамира утверждает, что такие интерактивные системы доказательств с короткими диалогами существуют для всех языков L, для которых существует распознающие алгоритмы, использующие полиномиальную память. В частности, так можно за полиномиальное время доказывать, что в графе нет гамильтонова пути.
Понятие доказательства встречается не только в математике и информатике, но и в юриспруденции. Например, обвиняют человека в преступлении, он может доказать, что не был на месте преступления, но не хочет сообщать, где он был на самом деле (например, он мог быть у любовницы или хочет скрыть свое местонахождение от конкурентов). Алиби не является преступлением, но его оглашение является очень нежелательным. Оказывается, что теоретически возможно доказывать так, чтобы не сообщать лишней информации, кроме доказываемого утверждения.
Рассмотрим пример: некоторая фирма пишет программы, которые быстро решают задачу об изоморфизме графов, но бесплатная версия этой программы просто говорит, изоморфны графы или нет, не выдавая перестановку в случае, когда графы изоморфны. Чтобы получать перестановку, нужно купить платную версию программы. Но между тем разработчики хотят, чтобы пользователь мог убедиться в том, что графы, действительно, изоморфны, но чтобы эта информация не помогла пользователю найти этот изоморфизм самостоятельно. Это можно сделать следующим образом: если графы G0 и G1 изоморфны, то можно выбрать случайную перестановку π и выдать граф G2=π (G1) и предложить пользователю решить, изоморфизм каких графов он хочет получить G0 и G2 или G1 и G2. Программа ответит ровно на один из этих запросов. Если программа знает изоморфизм, то она без труда ответит на запрос пользователя, если же изоморфизма нет, то как минимум для одного из вариантов запроса пользователя выдать ответ не получится. И если пользователь будет выбирать запрос случайным образом, то вероятность, что изоморфизм между выбранными пользователем вариантами есть, не превосходит 1/2. Ошибку можно уменьшить, повторяя этот процесс: выбирая новую перестановку и предлагая пользователю выбрать новый вариант.
Оказывается, что для каждого языка из класса NP при некотором криптографическом предположении можно построить такое интерактивное доказательство принадлежности, которое не даст никакой информации о классическом доказательстве принадлежности (которое существует для любого языка из класса NP). Упомянутое криптографическое предположение — это существование односторонних функций, т.е. функций, которые легко вычислить, но трудно обратить. К примеру, многие верят, что функция, которая по двум n битным числам выдает их произведение, является односторонней.
Пусть учитель математики дает своим ученикам домашнее задание, они ему сдают тетради с решением. Любой учитель математики мечтает, чтобы можно было проверить решение, не читая его полностью. Вариант проверять решение только по ответам плохой, поскольку ответ можно списать или угадать и также это не помогает в задачах на доказательство, в которых ответов как таковых и нет. Оказывается, эта мечта учителей достижима и любое доказательство можно переписать таким образом, чтобы для проверки его достаточно было посмотреть на константное число битов доказательства.
Приведем пример для языка пар неизоморфных графов GNI. В нашем примере доказательство будет экспоненциальной длины, а именно для графов на n вершинах доказательство будет иметь размер 2n(n-1)/2, тут n(n-1)/2 — это максимальное число ребер, которое может иметь граф на n вершинах. Доказательство неизоморфности пары графов G0 и G1 — это битовая строка w длины 2n(n-1)/2, которая проиндексирована всеми различными графами на n вершинах. Бит строки w, соответствующий графу H равен нулю, если H изоморфен G0, единице, если граф изоморфен G1, и равен чему угодно, если граф H не изоморфен ни G0, ни G1. На рисунке приведен пример такой строки w для двух неизоморфных графов на трех вершинах:

Проверка такого доказательства похожа на интерактивное доказательство: надо бросить монетку (взять случайное i из {0,1}), случайную перестановку σ и посмотреть на бит доказательства, соответствующий графу σ(Gi), если он совпадает с i, то принять такое доказательство, если не совпадает с i, то отвергнуть. В случае, когда графы G0 и G1 неизоморфны, то такое доказательство будет приниматься. Если графы G0 и G1 изоморфны, то граф σ(Gi) с равной вероятностью может быть перестановкой G0 и G1, следовательно, доказательство будет принято с вероятностью не больше 1/2. Повторив такую проверку 10 раз для независимых случайных выборов i и σ, можно понизить вероятность ошибки до 1/1024.
Недостаток приведенного выше доказательства в том, что оно имеет экспоненциальный размер. Однако знаменитая PCP-теорема (PCP — это сокращение от probabalistically checkable proofs) утверждает, что для каждого языка из класса NP существует доказательство принадлежности языку полиномиального размера, и для проверки этого доказательства достаточно прочитать константное число битов этого доказательства. Более того, обычное доказательство (которое существует по определению класса NP) можно за полиномиальное время переделать в доказательство, которое можно вероятностно проверять.
PCP-теорема — это не только забавный факт, но и мощный инструмент для доказательства трудности приближенных решений для оптимизационных задач. Напомним, что независимым множеством в графе называется множество вершин графа, между которыми нет ребер графа. Известно, что задача нахождения максимального независимого множества в графе является NP-трудной, это, в частности, означает, что если есть полиномиальный от числа вершин графа алгоритм, который находит максимальное независимое множество в графе, то P=NP. С помощью PCP-теоремы можно доказать, что NP-трудной задачей является нахождение не только максимального независимого множества, но и приближенно максимального (с константным приближением). В частности, если существует алгоритм, которой за полиномиальное время в графе находит независимое множество, которое не более, чем в 1000 раз меньше максимального, то из этого следует, что P=NP.
Литература, в которой можно найти строгие формулировки и доказательства всех упомянутых в статье утверждений:
Интересующимся теоретической информатикой рекомендуется обратить внимание на магистратуру Академического университета.

Чтобы объяснить, о какого рода доказательствах пойдет речь, рассмотрим пример: есть компьютерная программа, авторы которой утверждают, что программа делает что-то определенное (конкретные примеры будут чуть позже). Программу можно запустить и получить ответ. А как можно удостовериться, что программа делает то, что должна делать? Хорошо бы, если кроме ответа программа выдавала бы доказательство того, что этот ответ правильный.
Рассмотрим более конкретный пример: мы хотим иметь программу, которая в двудольном графе находит паросочетание максимального размера вместе с доказательством его максимальности.

Напомним, что граф называется двудольным, если его вершины можно покрасить в два цвета так, что ребра графа соединяют вершины разных цветов. Паросочетанием в графе называется такое множество ребер, что никакие два из них не имеют общего конца. Множество вершин графа называется покрывающим, если каждое ребро графа имеет как минимум один конец в этом множестве. Теорема Кенига гласит, что в двудольном графе размер максимального паросочетания совпадает с размером минимального покрывающего множества. Таким образом, чтобы доказать, что паросочетание является максимальным, можно предъявить, покрывающее множество, размер которого совпадает с размером данного паросочетания. Действительно, это покрывающее множество будет минимальным, поскольку каждое покрывающее множество обязано покрыть хотя бы один конец каждого ребра этого паросочетания. Например, в графе на рисунке паросочетание (M1, G3), (M2, G2), (M4,G1) будет максимальным, поскольку есть покрывающее множество размера 3, которое состоит из G2, G3 и M4. Отметим, что проверить такое доказательство гораздо проще, чем вычислять максимальное паросочетание: достаточно проверить, что размер паросочетания совпадает с размером покрывающего множества и проверить, что все ребра покрыты.
Рассмотрим еще один пример, допустим нам нужна программа, которая проверяет систему нестрогих линейных неравенств с рациональными коэффициентами на совместность (напомним, что система неравенств называется совместной, если можно подобрать такие значения переменных, что все неравенства выполняются).

Как можно доказать правильность результата? Если система совместна, то доказательством совместности может стать решение этой системы (нетрудно доказать, что если у такой системы есть решение, то есть и рациональное решение, т.е. его можно записать). А как доказать, что система несовместна? Оказывается, что это сделать можно с помощью леммы Фаркаша, которая утверждает, что если система нестрогих линейных неравенств несовместна, то можно сложить эти неравенства с неотрицательными коэффициентами и получить противоречивое неравенство 0≥1. Например, система на рисунке несовместна, и если сложить первое уравнение с коэффициентом 1, второе с коэффициентом 2, а третье с коэффициентом 1, то получится 0≥1. Доказательством несовместности будет как раз набор неотрицательных коэффициентов.
В этой статье мы поговорим о том, нужны ли доказательства, или проверка доказательства всегда не проще, чем самостоятельное решение задачи. (В примере про максимальное паросочетание мы не доказали, что не существует алгоритма, решающего задачу за то же время, сколько занимает проверка доказательства.) Если мы не ограничиваем размер доказательства, то окажется, что доказательства нужны, а если будем требовать, чтобы доказательства были короткими, то вопрос о нужности доказательств эквивалентен важнейшему открытому вопросу о равенстве классов P и NP. Потом мы поговорим об интерактивных доказательствах (доказательства в диалоге). Обсудим криптографические доказательства, которые не разглашают лишнюю информацию, кроме верности доказываемого утверждения. И закончим обсуждением вероятностно проверяемых доказательств и знаменитой PCP-теоремы, которая используется для доказательства трудности приближения оптимизационных задач.
В этой статье мы не будем касаться автоматического доказательства теорем и доказательства корректности программ, хотя эти темы тоже достаточно интересны.
Нужны ли доказательства?
Языком называется множество строк над некоторым конечным алфавитом. В теоретической информатике обычно рассматривают доказательства утверждений вида x∈L, где L — язык, а x — некоторая строка. Утверждения такого вида обобщают математические теоремы, поскольку любая математическая теорема гласит, что утверждение, записанное на формальном языке, принадлежит множеству истинных утверждений.
Системой доказательств для языка L называется алгоритм A(x,w), который получает на вход две строки: x и w и проверяет, что строка w является доказательством принадлежности x∈L. От системы доказательств требуют два свойства: корректность и полноту. Корректность утверждает, что если для некоторых строк x и w алгоритм A(x,w) выдает 1, то x∈L. Полнота утверждает, что для каждого x∈L существует такая строка w, что алгоритм A(x,w) выдает 1.
Языки, для которых существуют системы доказательств, называются перечислимыми языками. Если вы сталкивались с другим определением перечислимого языка, то в качестве упражнения, докажите их эквивалентность.
Язык L называется разрешимым, если существует такой алгоритм B, что при x∈L алгоритм B(x) выдает 1, а при x∉L выдает 0. Любой разрешимый язык имеет систему доказательств, в которой доказательство пустое. Естественный вопрос, обязательно ли, что для любого языка, для которого есть система доказательств, найдется и разрешающий алгоритм. Ответ на этот вопрос известен, существуют языки, для которых есть системы доказательств, но для которых нет разрешающего алгоритма. Придумать какой-то пример такого языка несложно, сложнее придумать естественный пример. Рассмотрим язык, который состоит из многочленов с целыми коэффициентами от многих переменных, которые обращаются в ноль хотя бы при каком-то целочисленном значении переменных. Система доказательств для такого языка строится просто: доказательством будет целочисленное значение переменных, в которых многочлен обращается в ноль. DPRM-теорема (названа по авторам: Дэвис, Путнам, Робинсон и Матияесевич) утверждает, что этот язык не является разрешимым, т.е. не существует алгоритма, который проверит, обращается ли многочлен в ноль в целых точках. Последний шаг в доказательстве этой теоремы принадлежит академику Ю. В. Матиясевичу и эта теорема дает отрицательный ответ на 10-ю проблему Гильберта.
Короткие доказательства
Пока мы не накладывали никаких ограничений на алгоритм, который проверяет доказательство и на размер доказательства. Будет ли полезным доказательство корректности результата некоторой программы, если время, которое потребуется на проверку доказательства больше, чем на выполнения самой программы? Кажется, что такие доказательства бессмысленны, поэтому будем требовать, чтобы алгоритм A(x,w) в определении системы доказательств работал бы полиномиальное от длины строки x и от длины доказательства w время, такие системы доказательств будем называть эффективными.

Будем говорить, что язык L принадлежит классу NP, если для него есть эффективная система доказательств и полином p, что для любого x∈L существует доказательство принадлежности x∈L длины не большей, чем p(|x|). Язык L принадлежит классу P, если существует полиномиальный по времени алгоритм, который проверяет принадлежность входной строки языку L. Класс P содержится в классе NP, поскольку для каждого языка L из P, алгоритм, проверяющий принадлежность L, сам и будет системой доказательств, если считать, что он игнорирует доказательство. На данный момент неизвестно, существуют ли языки из класса NP, которые не принадлежат классу P. Вопрос о равенстве классов P и NP входит в список семи задач тысячелетия, составленный институтом Клэя; за решение этой задачи объявлен приз в миллион долларов. Многие слышали про список задач тысячелетия в связи с доказательством гипотезы Пуанкаре Г. Я. Перельманом. Большинство специалистов полагают, что классы P и NP не совпадают.
Рассмотрим примеры языков из класса NP:
- Язык составных чисел лежит в классе NP. Чтобы доказать, что число n составное достаточно предъявить два целых числа a и b, которые больше единицы и n=ab. Язык простых чисел тоже лежит в классе NP, но доказать это сложнее. Впрочем, в 2002 году Каял и Саксена доказали, что язык простых (а, следовательно, и составных) чисел лежит в классе P.
- Рассмотрим язык GI, который состоит из пар изоморфных графов. Мы считаем, что вершины графов пронумерованы числами от 1 до n, каждое
ребро соединяет ровно одну пару вершин. Два графа G1(V1,E1) и G2(V2,E2) называются изоморфными, если вершины первого графа можно перенумеровать так, чтобы первый граф стал совпадать со вторым графом. Это значит, что после перенумерации множество ребер первого графа совпадет с множеством ребер второго графа. Язык GI лежит в классе NP, доказательством изоморфности графов будет перестановка вершин первого графа, которая задает изоморфизм. Лежит ли язык GI в классе P, является открытым вопросом. Рассмотрим также язык GNI, который состоит из пар неизоморфных графов на одинаковом числе вершин. Про язык GNI неизвестно, лежит ли он в NP, поскольку непонятно как коротко доказать, что два графа неизоморфны.
- Рассмотрим язык HamPath, который состоит из графов, в которых есть гамильтонов путь, т.е. такой путь, который ровно по одному разу проходит через каждую вершину. Этот язык лежит в классе NP, поскольку в качестве доказательства наличия пути можно использовать сам путь. Про этот язык неизвестно лежит ли он в классе P, но известно, что он является NP-полным. Последнее в частности означает, что HamPath не лежит в P, если P≠NP. Дополнение языка HamPath совпадает с множеством графов, в которых нет гамильтонова пути. Лежит ли дополнение HamPath в классе NP неизвестно.
Интерактивные доказательства
До сих пор доказательства, которые мы рассматривали, были очень похожими на привычные нами, а именно, доказательство — это некоторый текст, который, хотя и непонятно как придумывать, но легко проверить, есть алгоритм, который проверяет корректность доказательства. Т.е., чтобы придумать доказательство нужно иметь какие-то специальные способности, а проверить доказательство может каждый. На самом деле совсем не все доказательства современной математики обладают этим свойством. Во-первых, доказательства не пишут на удобном для автоматической проверки формальном языке, а во-вторых, чтобы понять доказательство в некоторых областях, нужно несколько лет потратить на изучение этой области.
В математических кружках для школьников часто практикуется такой формат занятий: детям выдается набор задач, когда ребенок считает, что он решил задачу, то он устно рассказывает решение преподавателю. И происходит диалог между преподавателем и учеником, который либо убеждает преподавателя в том, что задача решена, либо не убеждает.
Рассмотрим пример интерактивного доказательства: есть программа, которая решает задачу изоморфизма графов. В случае, когда графы изоморфны, программа может доказать правильность своего ответа, выдав перестановку, задающую изоморфизм. Покажем, как можно в диалоге доказать, что графы неизоморфны. Пусть пользователь спросил программу, изоморфны ли графы G0 и G1 и получил ответ, что они неизоморфны. После этого пользователь бросает монетку (выбирает случайный элемент i из множества {0,1}) и выбирает случайную перестановку n-элементного множества (при этом все перестановки считаются равновероятными) σ. И спрашивает программу, изоморфны ли графы G0, σ (Gi). Если i=0, то от программы ожидается ответ, что графы изоморфны, а если i=1, то от программы ожидается, что графы неизоморфны. Если графы G0 и G1 действительно были неизоморфны, то программа без труда даст правильный ответ на этот вопрос. А если же G0 и G1 были изоморфны, то граф σ (Gi) с равной вероятностью может быть как перестановкой G0, так и перестановкой G1, следовательно программа выдаст ожидаемый ответ с вероятностью не больше, чем 1/2. Вероятность ошибки можно уменьшить, повторив алгоритм n раз и решить, что алгоритм верно работает, если в каждом из n запусков был дан верный ответ; вероятность ошибки в таком случае не превосходит 1/2n.
В рассмотренном только что примере доказательство — это диалог между доказывающим (программой) и проверяющим (пользователем), при этом доказывающий может быть устроен очень сложно, а проверяющий может делать только простые вещи (производить полиномиальные по времени вычисления). Если элемент x∈L, то доказывающий должен с вероятностью 1 убедить в этом проверяющего, а если x∉L, то проверяющий должен принять такое доказательство с вероятностью не больше, чем 1/10. Теорема Шамира утверждает, что такие интерактивные системы доказательств с короткими диалогами существуют для всех языков L, для которых существует распознающие алгоритмы, использующие полиномиальную память. В частности, так можно за полиномиальное время доказывать, что в графе нет гамильтонова пути.
Доказательства с нулевым разглашением

Понятие доказательства встречается не только в математике и информатике, но и в юриспруденции. Например, обвиняют человека в преступлении, он может доказать, что не был на месте преступления, но не хочет сообщать, где он был на самом деле (например, он мог быть у любовницы или хочет скрыть свое местонахождение от конкурентов). Алиби не является преступлением, но его оглашение является очень нежелательным. Оказывается, что теоретически возможно доказывать так, чтобы не сообщать лишней информации, кроме доказываемого утверждения.
Рассмотрим пример: некоторая фирма пишет программы, которые быстро решают задачу об изоморфизме графов, но бесплатная версия этой программы просто говорит, изоморфны графы или нет, не выдавая перестановку в случае, когда графы изоморфны. Чтобы получать перестановку, нужно купить платную версию программы. Но между тем разработчики хотят, чтобы пользователь мог убедиться в том, что графы, действительно, изоморфны, но чтобы эта информация не помогла пользователю найти этот изоморфизм самостоятельно. Это можно сделать следующим образом: если графы G0 и G1 изоморфны, то можно выбрать случайную перестановку π и выдать граф G2=π (G1) и предложить пользователю решить, изоморфизм каких графов он хочет получить G0 и G2 или G1 и G2. Программа ответит ровно на один из этих запросов. Если программа знает изоморфизм, то она без труда ответит на запрос пользователя, если же изоморфизма нет, то как минимум для одного из вариантов запроса пользователя выдать ответ не получится. И если пользователь будет выбирать запрос случайным образом, то вероятность, что изоморфизм между выбранными пользователем вариантами есть, не превосходит 1/2. Ошибку можно уменьшить, повторяя этот процесс: выбирая новую перестановку и предлагая пользователю выбрать новый вариант.
Оказывается, что для каждого языка из класса NP при некотором криптографическом предположении можно построить такое интерактивное доказательство принадлежности, которое не даст никакой информации о классическом доказательстве принадлежности (которое существует для любого языка из класса NP). Упомянутое криптографическое предположение — это существование односторонних функций, т.е. функций, которые легко вычислить, но трудно обратить. К примеру, многие верят, что функция, которая по двум n битным числам выдает их произведение, является односторонней.
Вероятностно проверяемые доказательства
Пусть учитель математики дает своим ученикам домашнее задание, они ему сдают тетради с решением. Любой учитель математики мечтает, чтобы можно было проверить решение, не читая его полностью. Вариант проверять решение только по ответам плохой, поскольку ответ можно списать или угадать и также это не помогает в задачах на доказательство, в которых ответов как таковых и нет. Оказывается, эта мечта учителей достижима и любое доказательство можно переписать таким образом, чтобы для проверки его достаточно было посмотреть на константное число битов доказательства.
Приведем пример для языка пар неизоморфных графов GNI. В нашем примере доказательство будет экспоненциальной длины, а именно для графов на n вершинах доказательство будет иметь размер 2n(n-1)/2, тут n(n-1)/2 — это максимальное число ребер, которое может иметь граф на n вершинах. Доказательство неизоморфности пары графов G0 и G1 — это битовая строка w длины 2n(n-1)/2, которая проиндексирована всеми различными графами на n вершинах. Бит строки w, соответствующий графу H равен нулю, если H изоморфен G0, единице, если граф изоморфен G1, и равен чему угодно, если граф H не изоморфен ни G0, ни G1. На рисунке приведен пример такой строки w для двух неизоморфных графов на трех вершинах:

Проверка такого доказательства похожа на интерактивное доказательство: надо бросить монетку (взять случайное i из {0,1}), случайную перестановку σ и посмотреть на бит доказательства, соответствующий графу σ(Gi), если он совпадает с i, то принять такое доказательство, если не совпадает с i, то отвергнуть. В случае, когда графы G0 и G1 неизоморфны, то такое доказательство будет приниматься. Если графы G0 и G1 изоморфны, то граф σ(Gi) с равной вероятностью может быть перестановкой G0 и G1, следовательно, доказательство будет принято с вероятностью не больше 1/2. Повторив такую проверку 10 раз для независимых случайных выборов i и σ, можно понизить вероятность ошибки до 1/1024.
Недостаток приведенного выше доказательства в том, что оно имеет экспоненциальный размер. Однако знаменитая PCP-теорема (PCP — это сокращение от probabalistically checkable proofs) утверждает, что для каждого языка из класса NP существует доказательство принадлежности языку полиномиального размера, и для проверки этого доказательства достаточно прочитать константное число битов этого доказательства. Более того, обычное доказательство (которое существует по определению класса NP) можно за полиномиальное время переделать в доказательство, которое можно вероятностно проверять.
PCP-теорема — это не только забавный факт, но и мощный инструмент для доказательства трудности приближенных решений для оптимизационных задач. Напомним, что независимым множеством в графе называется множество вершин графа, между которыми нет ребер графа. Известно, что задача нахождения максимального независимого множества в графе является NP-трудной, это, в частности, означает, что если есть полиномиальный от числа вершин графа алгоритм, который находит максимальное независимое множество в графе, то P=NP. С помощью PCP-теоремы можно доказать, что NP-трудной задачей является нахождение не только максимального независимого множества, но и приближенно максимального (с константным приближением). В частности, если существует алгоритм, которой за полиномиальное время в графе находит независимое множество, которое не более, чем в 1000 раз меньше максимального, то из этого следует, что P=NP.
Ссылки
Литература, в которой можно найти строгие формулировки и доказательства всех упомянутых в статье утверждений:
- S. Arora, B. Barak, Computational Complexity: A modern Approach
- O. Goldreich, The Foundations of Cryptogtaphy
- Ю. В. Матиясевич, Десятая проблема Гильберта. — М.: Наука, 1993. — ISBN 502014326X
- Н.К. Верещагин, Теоретико-сложностные проблемы крипотграфии, конспект лекций
- Д.М. Ицыксон, Обзорный курс по теоретической информатике, конспект лекций
Интересующимся теоретической информатикой рекомендуется обратить внимание на магистратуру Академического университета.