SeptiM 9 фев 2016 в 19:17

Компоненты связности в динамическом графе за один проход

8 мин

19K

Блог компании Образовательные проекты JetBrainsАлгоритмы*Математика*

Туториал

Люди встречаются, люди ссорятся, добавляются и удаляют друзей в социальных сетях. Этот пост о математике и алгоритмах, красивой теории, любви и ненависти в этом непостоянном мире. Этот пост о поиске компонент связности в динамических графах.

Большой мир генерирует большие данные. Вот и на нашу голову свалился большой граф. Настолько большой, что мы можем удержать в памяти его вершины, но не ребра. Кроме того, относительно графа приходят обновления – какое ребро добавить, какое удалить. Можно сказать, что каждое такое обновление мы видим в первый и последний раз. В таких условиях необходимо найти компоненты связности.

Поиск в глубину/ширину здесь не пройдут просто потому, что весь граф в памяти не удержать. Система непересекающихся множеств могла бы сильно помочь, если бы ребра в графе только добавлялись. Что же делать в общем случае?

Задача. Дан неориентированный граф $G$ на $n$ вершинах. Изначально, граф – пустой. Алгоритму приходит последовательность обновлений $p_1, p_2, \dots, p_m$ , которую можно прочитать в заданном порядке ровно один раз. Каждое обновление – это команда удалить или добавить ребро между парой вершин $u_i$ и $v_i$ . Гарантируется, что ни в какой момент времени между парой вершин не будет удалено ребер больше чем есть. По прочтении последовательности алгоритм должен вывести все компоненты связности с вероятностью успеха $0.99$ . Разрешается использовать $O(n \log^c n)$ памяти, где $c$ – некоторая константа.

Решение задачи состоит из трех ингредиентов.

Матрица инцидентности как представление.
Метод стягивания как алгоритм.
$L_0$ -сэмплирование как оптимизация.

Реализацию можно посмотреть на гитхабе: link.

Матрица инцидентности как представление

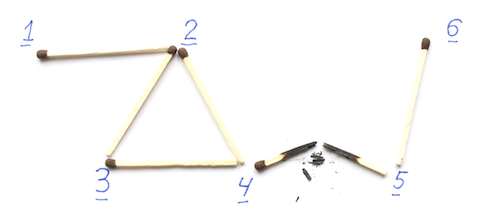
Первая структура данных для хранения графа будет крайне неоптимальна. Мы возьмем матрицу инцидентности $A$ размера $n \times \binom{n}{2}$ , в которой преимущественно будут нули. Каждая строка в матрице соответствует вершине, а столбец – возможному ребру. Пусть $u < v$ . Для пары вершин $u, v$ , соединенных ребром, зададим
$A_{u, (u, v)} = 1$ и $A_{v, (u, v)} = -1$ , в противном случае значения равны нулю.

Как пример, посмотрим на граф на картинке ниже.

Для него матрица инцидентности будет выглядеть так.

$\begin{array}{r|ccccccccccccccc} A & (1, 2) & (1, 3) & (1, 4) & (1, 5) & (1, 6) & (2, 3) & (2, 4) & (2, 5) & (2, 6) & (3, 4) & (3, 5) & (3, 6) & (4, 5) & (4, 6) & (5, 6) \\ \hline 1 & +1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 2 & -1 & 0 & 0 & 0 & 0 & +1 & +1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 3 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & +1 & 0 & 0 & 0 & 0 & 0 \\ 4 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 & -1 & 0 & 0 & 0 & 0 & 0 \\ 5 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & +1 \\ 6 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 \\ \end{array}$

Невооруженным глазом видно, что у такого представления есть серьезный недостаток – размер $O(n^3)$ . Мы его оптимизируем, но позже.

Есть и неявное преимущество. Если взять множество вершин $S$ и сложить все вектора-строки матрицы $A$ , которые соответствуют $S$ , то ребра между вершинами $S$ сократятся и останутся только те, что соединяют $S$ и $V \backslash S$ .

Например, если взять множество $S = \{3, 4, 5\}$ и сложить соответствующие вектора, мы получим

$\begin{array}{r|ccccccccccccccc} A & (1, 2) & (1, 3) & (1, 4) & (1, 5) & (1, 6) & (2, 3) & (2, 4) & (2, 5) & (2, 6) & (3, 4) & (3, 5) & (3, 6) & (4, 5) & (4, 6) & (5, 6) \\ \hline 3, 4, 5 & 0 & 0 & 0 & 0 & 0 & -1 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & +1 \end{array}$

Ненулевые значения стоят у ребер $(2, 3)$ , $(2, 4)$ и $(5, 6)$ .

Стягивание графа как алгоритм

Поймем, что такое стягивание ребра. Вот есть у нас две вершины $u$ и $v$ , между ними есть ребро. Из $u$ и $v$ могут исходить и другие ребра. Стягивание ребра $(u, v)$ это процедура, когда мы сливаем вершины $u$ и $v$ в одну, скажем $w$ , ребро $(u, v)$ удаляем, а все оставшиеся ребра, инцидентные $u$ и $v$ , проводим в новую вершину $w$ .

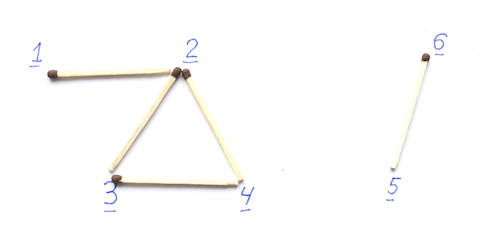
Интересная особенность: в терминах матрицы инцидентности, чтобы стянуть ребро $(u, v)$ , достаточно сложить соответствующие вектора-строки. Само ребро $(u, v)$ сократится, останутся только те, что идут наружу.

Теперь алгоритм. Возьмем граф и для каждой неизолированной вершины выберем соседа.

Стянем соответствующие ребра.

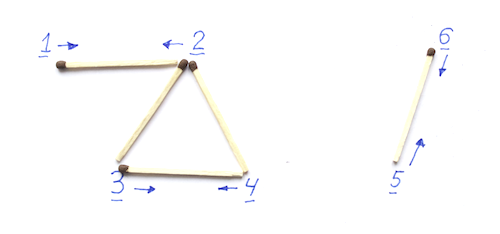
Повторим итерацию $\log n$ раз.

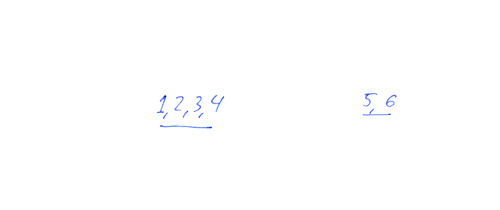
Заметим, что после каждой итерации стягивания компоненты связности нового графа взаимно-однозначно сопоставляются компонентам старого. Мы можем даже помечать, какие вершины были слиты в результирующие, чтобы потом восстановить ответ.

Заметим также, что после каждой итерации, любая компонента связности хотя бы из двух вершин уменьшается как минимум в два раза. Это естественно, поскольку в каждую вершину новой компоненты было слито как минимум две вершины старой. Значит, после $\log n$ итераций в графе останутся только изолированный вершины.

Переберем все изолированный вершины и по истории слияний восстановим ответ.

$L_0$ -сэмплирование как оптимизация

Все было бы замечательно, но приведенный алгоритм работает что по времени, что по памяти $O(n^3)$ . Чтобы его оптимизировать, мы построим скетч – специальную структуру данных для компактного представления векторов-строк.

От скетча потребуется три свойства.

Во-первых, компактность. Если мы строим скетч для вектора $a$ размера $O(n)$ , то сам скетч $\sigma(a)$ должен быть размера $O(\log^c n)$ .

Во-вторых, сэмплирование. На каждой итерации алгоритма, нам требуется выбирать соседа. Мы хотим способ получать индекс хотя бы одного ненулевого элемента, если такой есть.

В-третьих, линейность. Если мы построили для двух векторов $a$ и $b$ скетчи $\sigma(a)$ и $\sigma(b)$ . Должен быть эффективный метод, получить скетч $\sigma(a + b) = f(\sigma(a), \sigma(b))$ . Это поможет стягивать ребра.

Мы воспользуемся решением задачи $L_0$ -сэмплирования.

Задача. Дан вектор нулевой вектор $a = \langle a_1, a_2, \dots, a_n \rangle$ размерности $n$ . Алгоритму приходит последовательность из $m$ обновлений вида $(i, \Delta)$ : прибавить $\Delta$ к значению $a_i$ . $\Delta$ может быть как положительным, так и отрицательным целым числом. Результирующий вектор на некоторых позициях может иметь ненулевые значения. Эти позиции обозначим через $I$ . Требуется выдать любую позицию из $I$ равновероятно. Все обновления нужно обработать за один проход, можно использовать $O(\log^c n)$ памяти. Гарантируется, что максимальное значение в $a_i$ укладывается в $O(\log n)$ бит.

1-разреженные вектор

Для начала мы решим более простую задачу. Пусть у нас есть гарантия, что конечный вектор содержит ровно одну ненулевую позицию. Будем говорить, что такой вектор – 1-разреженный. Будем поддерживать две переменных $S_0 = \sum_i a_i$ и $S_1 = \sum_i i \cdot a_i$ . Поддерживать их просто: на каждом обновлении прибавляем к первой $\Delta$ , ко второй $i \cdot \Delta$ .

Обозначим искомую позицию через $i'$ . Если она только одна, то $S_0 = a_{i'}$ и $S_1 = i' \cdot a_{i'}$ . Чтобы найти позицию, считаем $i' = S_1 / S_0$ .

Можно вероятностно проверить, является ли вектор 1-разреженным. Для этого возьмем простое число $p > 4 \cdot n$ , случайное целое $z \in [0, p)$ и посчитаем переменную $T = \sum_i a_i \cdot z^i % p$ . Вектор проходит тест на 1-разреженность, если $S_0 \neq 0$ и $T = S_0 \cdot z^{S_1 / S_0}$ .

Очевидно, что если вектор действительно 1-разреженный, то

$T = \sum_i a_i \cdot z^i = a_{i'} \cdot z^{i'} = S_0 \cdot z^{S_1 / S_0}$

и тест он пройдет. В противном случае, вероятность пройти тест не более $0.25$ (на самом деле, максимум $n / p$ ).

Почему?

В терминах многочлена, вектор проходит тест, если значения полинома

$p(z) = \sum_i a_i \cdot z^i - S_0 \cdot z^{S_1 / S_0}$

в случайно выбронной точке $z$ равно нулю. Если вектор не является 1-разреженным, то $p(z)$ не является тождественно равным нулю. Если мы прошли тест, мы угадали корень. Максимальная степень полинома – $n$ , значит, корней не более $n$ , значит, вероятность их угадать не более $n / p$ .

Если мы хотим повысить точность проверки до произвольной вероятности $1 - \delta$ , то нужно посчитать значение $T$ на $O(\log \delta^{-1})$ случайных $z$ .

$s$ -разреженный вектор

Теперь попробуем решить задачу для $s$ -разреженного вектора, т.е. содержащего не более $s$ ненулевых позиций. Нам потребуется хэширование и предыдущий метод. Общая идея – восстановить вектор целиком, а потом выбрать какой-нибудь элемент случайно.

Возьмем случайную 2-независимую хэш-функцию $h : [n] \rightarrow [2s]$ . Эта такая функция, которая два произвольных различных ключа распределяет равновероятно независимо.

Подробнее про хэш-функции

В алгоритмах есть два принципиально разных подхода к хэш-функциям. Первый основывается на том, что данные более менее случайные, и наша любимая хэш-функция размешает их правильно. Второй, на том, что данные может подбирать злой противник, и единственный шанс спасти алгоритм от лишних вычислений и прочих проблем – это выбирать хэш-функцию случайно. Да, иногда может работать плохо, но зато мы можем померять, насколько плохо. Здесь идет речь о втором подходе.

Хэш-функция выбирается из семества функций. Например, если мы хотим размешать все числа от

до $p - 1$ , можно взять случайные $a$ и $b$ и определить хэш-функцию

$h_{a, b}(x) = a \cdot x + b \text{ mod } p.$

Функции для всех возможнных $a, b \in [p]$ задают семейство хэш-функций. Случайно выбрать хэщ-функцию – это по сути случайно выбрать те самые $a$ и $b$ . Выбираются они обычно равновероятно из множества $[p]$ .

Замечательное свойство у приведенного примера, что два любых различных ключа распределяются случайно независимо. Формально, для любых различных $x_1, x_2 \in [p]$ и любых, возможно одинаковых, $y_1, y_2 \in [p]$ вероятность

$\textbf{Pr}\left[ h(x_1) = y_1 \text{ and } h(x_2) = y_2 \right] = p^{-2}.$

Такое свойство называется 2-независимостью. Иногда, вероятность может быть не $p^{-2}$ , а $p^{-2} \pm \varepsilon$ , где $varepsilon$ какая-то разумно маленькая величина.

Есть обобщение 2-независимости — $k$ -независимость. Это когда функция распределяет не 2, $k$ произвольных ключей независимо. Полиномиальные хэш-функции с $k$ случайными коэффициентами обладают таким свойством.

$p(x) = \sum_{i = 0}^{k - 1} a_i \cdot x^i \text{ mod } p$

У $k$ -независимости есть одно неприятное свойство. С ростом $k$ функция занимает все больше памяти. Это свойство не зависит от какой-то конкретной реализации, а просто общее информационное свойство. Поэтому чем меньшей независимостью мы можем обойтись, тем легче на жить.

Возьмем хэш-таблицу размера $2s$ . В каждой ячейке таблицы будет сидеть алгоритм для 1-разереженного вектора. Когда нам приходит обновление $(i, \Delta)$ , мы отправляем это обновление алгоритму в ячейке $h(i)$ .
Можно посчитать, что для отдельной ячейки, вероятность что там произойдет коллизия хотя бы по двум ненулевым координатам будет не более $0.4$ .

Почему?

Вероятность, что другой элемент не попадет в ячейку к нам $(1 - 1 / 2s)$ . Вероятность, что все не попадут к нам: $(1 - 1 / 2s)^{s- 1}$ . Вероятность, что хоть кто-нибудь попадет $1 - (1 - 1 /2s)^{s - 1}$ . Можно заметить, что это функция монотонно возрастающая. Я здесь просто приведу картинку:

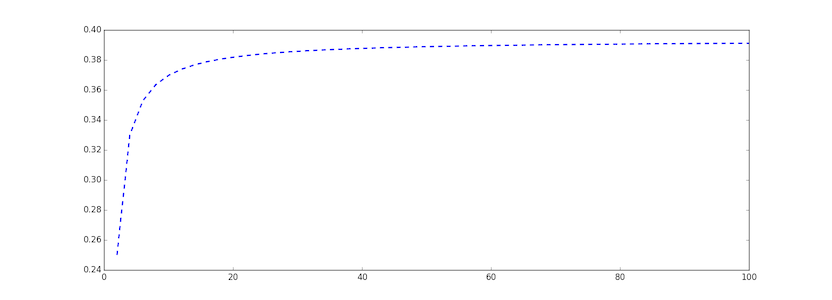
В пределе функция дает значение $1 - e^{-0.5} \leq 0.4$ .

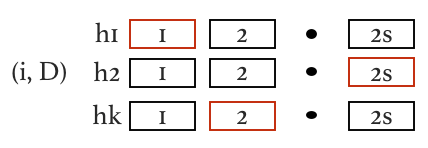
Пусть мы хотим восстановить все координаты с вероятностью успеха $1 - \delta$ , или с вероятностью провала $\delta$ . Возьмем не одну хэш-таблицу, а сразу $k = O(\log (s \cdot (\delta / 2)^{-1}))$ . Несложно понять, что вероятность провала в декодировании отдельной координаты будет $(\delta / 2) / s$ . Вероятность провала в декодировании хотя бы одной из $s$ координат $\delta / 2$ . Если в сумме декодирование для 1-разреженных векторов работает с вероятностью провала $\delta / 2$ , то мы победили.

Итоговый алгоритм таков. Берем $O(\log(s \cdot \delta^{-1}))$ хэш-таблиц размера $2s$ . В каждой ячейке алгоритма будет находиться свой декодер для 1-разреженного вектора с вероятностью провала $\delta / 2 k s$ .

Каждое обновление $(i, \Delta)$ обрабатывается в каждой хэш-таблице отдельно алгоритмом в ячейке $h_j(i)$ .

По завершении, извлекаем из всех успешно отработавших 1-декодеров по координате и сливаем их в один список.

Максимум, в общей таблице будет $k \cdot s$ затронутых 1-декодеров. Поэтому суммарная вероятность, что один из 1-декодеров отработает неверно не превысит $k s \cdot \delta / 2 ks = \delta / 2$ . Также вероятность, что хотя бы одна координата не будет восстановлена не превышает $\delta / 2$ . Итого, вероятность провала алгоритма $\delta$ .

Еще одно хэширование для общего случая

Последний шаг в $L_0$ -сэмплировании, это понять, что делать с общим случаем. Мы снова воспользуемся хэшированием. Возьмем $O(s)$ -независимую хэш-функцию $h : [n] \rightarrow [2^k]$ для некоторого $2^k \geq n^3$ .

Будем говорить, что обновление $(i, \Delta)$ является $j$ -интересным, если $h(i) \text{ mod } 2^j = 0$ . Иначе говоря, в бинарной записи $h(i)$ содержит $j$ нулей в конце.

Запустим алгоритм для $s$ -разреженного вектора параллельно на $\log n$ уровнях. На уровне $j$ будем учитывать только $j$ -интересные обновления. Несложно понять, что чем больше $j$ , тем меньше шансов (а шансов $2^{-j}$ ) у обновления быть учтенным.

Найдем первый уровень с наибольшим $j$ , где приходили хоть какие-то обновления, и попытаемся его восстановить. Если восстановление пройдет успешно, вернем случайно выбранную позицию.

Есть несколько моментов, на которые хочется вкратце обратить внимание.

Во-первых, как выбирать $s$ . В общем случае вектор может иметь более чем $s$ ненулевых позиций, но с каждым увеличением $j$ на единицу, мат. ожидание ненулевых позиций падает ровно в 2 раза. Можно выбрать такой уровень, при котором мат.ожидание будет между $s / 4$ и $s / 2$ . Тогда из оценок Чернова и $O(s)$ независимости хэш-функции, вероятность, что вектор будет нулевым или иметь более чем $s$ ненулевых позиций, окажется экспоненциально мала.

Это определяет выбор $s = O(\log \delta^{-1})$ , где $\delta$ – допустимая вероятность провала.

Во-вторых, из $O(s)$ -независимости хэш-функции следует, что для любой позиции вероятность пройти фильтр окажется равной. Поскольку $s$ -разреженные вектора мы уже умеем восстанавливать, то получить равномерное распределение уже тривиально.

Итого, мы научились выбирать случайную ненулевую позицию согласно равномерному распределению.

Смешать, но не взбалтывать

Осталось понять, как все совместить. Нам известно, что в графе $n$ вершин. Для каждой вершины, точнее каждого вектора-строки в матрице инцидентности, заведем $\log n$ скетчей $\sigma_1(A_v), \sigma_2(A_v), \dots, \sigma_{\log n}(A_v)$ для $L_0$ -сэмплирования. На $i$ -ой итерации алгоритма стягивания будем использовать для сэмплирования $i$ -ые скетчи.

При добавлении ребра $(u, v)$ добавим во все скетчи вершин $u$ и $v$ соответствующие +1 и -1 соответственно.

Когда ребра закончатся и нас спросят про компоненты, запустим алгоритм стягивания. На $i$ -ой итерации, через $L_0$ -сэмплирование из скетча $\sigma_i(v)$ найдем соседа каждой вершине. Чтобы стянуть ребро $(u, v)$ , сложим все скетчи соответствующие $u$ и $v$ . У каждой новой вершины сохраним список вершин, которые были в нее слиты.

Все. В конце просто проходим по изолированным вершинам, по истории слияний восстанавливаем ответ.

Кто виноват и еще раз что делать

На самом деле тема этого поста возникла не просто так. В январе к нам, в Питер в CS Клуб, приезжал Илья Разенштейн (@ilyaraz), аспирант MIT, и рассказывал про алгоритмы для больших данных. Было много интересного (посмотрите описание курса). В частности Илья успел рассказать первую половину этого алгоритма. Я решил довести дело до конца и рассказать весь результат на Хабре.

В целом, если вам интересна математика, связанная с вычислительными процессами aka Theoretical Computer Science, приходите к нам в Академический Университет на направление Computer Science. Внутри научат сложности, алгоритмам и дискретной математике. С первого семестра начнется настоящая наука. Можно выбираться наружу и слушать курсы в CS Клубе и CS Центре. Если вы не из Питера, есть общежитие. Прекрасный шанс переехать в Северную Столицу.

Подавайте заявку, готовьтесь и поступайте к нам.

Источники

Теги:

Хабы: