dmitrifriend 25 фев в 13:04

Тест Grok-3 против DeepSeek-r1: когда бесплатный ИИ наступает на пятки платному

Средний

17 мин

19K

Блог компании BotHubИскусственный интеллектМашинное обучение*IT-компанииБудущее здесь

Обзор

Перевод

Автор оригинала: Шриджал Ачарья

Сегодня почти каждый, кто следит за миром искусственного интеллекта, слышал о модели DeepSeek‑r1 — открытой разработке из Китая, главная фишка которой — это полностью бесплатный и открытый исходный код, а по своим возможностям она способна соперничать с некоторыми платными моделями от OpenAI, такими как o1.

Но затем, 16 февраля, Илон Маск объявил о запуске Grok-3, назвав его «самым умным ИИ на планете»:

Интересно, как Grok-3 выглядит на фоне модели DeepSeek‑r1? Этот вопрос не давал мне покоя, и я решил проверить, кто из них сильнее в таких областях, как программирование, логика, математика и творческое письмо. Давайте разберёмся, оправдан ли весь этот ажиотаж вокруг Grok-3. Я протестировал обе модели, используя специально составленный список запросов, и тщательно оценил их способности в разных задачах.

Примечание: запросы и ответы на английском вы можете просмотреть в оригинальном обзоре (щёлкнув на ссылку «Автор оригинала» в начале статьи). Думаю, так будет удобнее, чем добавлять исходные тексты здесь.

Кратко о модели Grok-3

Grok-3 — это новейшая языковая модель от xAI, обладающая десятикратно возросшей вычислительной мощностью. В её арсенале есть специальные инструменты: DeepSearch — для пошагового логического рассуждения и Big Brain Mode — для работы с особенно сложными задачами. На данный момент Grok-3 находится в режиме бета‑тестирования, но действительно ли он настолько лучше, чем DeepSeek‑r1? Ведь, согласно официальным тестам, представленным командой xAI на запуске, Grok-3 обходит многие модели конкурентов по ключевым показателям.

Ответ на этот вопрос мы получим к концу статьи. Я использовал Chatbot Arena для тестирования обеих моделей бок о бок — на этом ресурсе можно было испытать раннюю версию Grok-3.

Логические задачи

Проверим, как модели обходят друг друга в задачах на логику.

Олимпийские спортсмены

ПРОМТ: Я сестра в семье трёх олимпийских спортсменов. Но эти двое — не мои сёстры. Как такое возможно?

GROK-3: Это возможно, если ваши братья — олимпийские спортсмены. Вы — их сестра, но они — ваши братья, а не сёстры. Всё логично.

DEEPSEEK‑R1: Всё дело в поле спортсменов. Говорящая — женщина, и у неё есть два брата, которые являются олимпийскими спортсменами. Поскольку siblings — это родные братья или сёстры, два спортсмена — её братья, а не сёстры. Таким образом, утверждение верно: она — их сестра, но они не её сёстры — они её братья.

Вердикт: обе модели решили эту задачу правильно, продемонстрировав верное логическое рассуждение.

Найди лжеца

Первая задача была довольной простой. Теперь — логическая загадка посложнее:

ПРОМТ: Вы встречаете трёх человек: Хариса, Энтони и Майкла. Харис говорит: «По крайней мере один из нас лжец». Энтони говорит: «Харис лжёт». Майкл говорит: «Энтони говорит правду». Кто из них лжёт, а кто говорит правду?

GROK-3:

Случай 1: Харис говорит правду
Харис утверждает: «По крайней мере один из нас лжец». Если это правда, значит, среди них действительно есть хотя бы один лжец.
• Если Харис честен, то сам он не лжёт. Значит, либо Энтони, либо Майкл (или оба) говорят неправду.
• Проверим слова Энтони: «Харис лжёт».
— Если Харис говорит правду, то заявление Энтони — ложь. Значит, Энтони лжец.
• Теперь слова Майкла: «Энтони говорит правду».
— Поскольку Энтони лжёт, Майкл, утверждающий, что Энтони честен, тоже говорит неправду.
Итого для первого случая:
• Харис — честен.
• Энтони — лжец.
• Майкл — лжец.
• Соответствует ли это утверждению Хариса, что «по крайней мере один из нас лжец»? Да, ведь лгут и Энтони, и Майкл.

Случай 2: Харис лжёт
• Если слова Хариса ложь, то его утверждение «по крайней мере один из нас лжец» должно быть ложным. Это значит, что лжецов среди них нет, и все трое говорят правду — противоречие!
• Если Харис лжёт, тогда Энтони прав, говоря: «Харис лжёт».
• Если Энтони прав, значит, Майкл тоже говорит правду, утверждая: «Энтони говорит правду».
• Но это невозможно: если Харис лжёт, то его слова ложны — а это противоречит тому, что все трое правдивы.
Итого для второго случая: Этот вариант приводит к логической несостыковке: нельзя, чтобы Харис лгал, ведь это рушит логику его же слов. Остаётся единственный вывод: Харис говорит правду.

Grok-3 продемонстрировал тщательный подход к решению задачи, последовательно разобрав оба возможных сценария и обосновав свой вывод шаг за шагом.

DEEPSEEK‑R1:

Харис утверждает: «По крайней мере один из нас лжец». Если бы это было ложью, то вышло бы, что все трое говорят правду, — но это противоречие. Значит, Харис говорит правду и среди них действительно есть хотя бы один лжец.
Энтони заявляет: «Харис лжёт». Поскольку Харис говорит правду, слова Энтони ложь.
Майкл поддерживает Энтони, говоря: «Энтони говорит правду». Но поскольку Энтони солгал, Майкл тоже говорит неправду.

Вывод:
• Харис — говорит правду.
• Энтони — лжёт.
• Майкл — лжёт.
Харис честен, а Энтони и Майкл лжецы.

Оба ИИ дали верные ответы, но рассуждения Grok-3 выглядят более развёрнутыми и логически выверенными.

Итог

Из этого теста видно, что обе модели продемонстрировали уверенные навыки логического мышления, корректно решив обе предложенные задачи. Однако подход Grok-3 порой кажется более глубоко проработанным и последовательным.

Математика

Учитывая, как модели справились с логическими задачами, я был уверен, что с математикой у них тоже не возникнет проблем. Начнём с простой задачи.

Сколько человек было в поезде?

ПРОМТ: В поезде ехали несколько человек. На первой остановке вышли 19 пассажиров, затем вошли 17. После этого в поезде оказалось 63 человека. Сколько человек было в поезде изначально?

GROK-3:

Решим задачу по шагам, чтобы выяснить, сколько человек было в поезде в самом начале.
1. Пусть — количество пассажиров в поезде до первой остановки.
2. На первой остановке вышли 19 человек, значит, осталось:

3. Затем вошли 17 человек, и количество пассажиров стало:

4. По условию после всех пересадок в поезде оказалось 63 человека, составим уравнение:

5. Решим его:

Итак, изначально в поезде было 65 пассажиров.

DEEPSEEK‑R1:

Пусть — начальное количество пассажиров в поезде.
1. После того как на первой остановке вышли 19 человек, в поезде осталось:

2. Затем вошли 17 человек, и число пассажиров стало:

3. По условию после всех пересадок в поезде оказалось 63 человека. Составим уравнение:

4. Упрощаем левую часть:

5. Находим x:

Проверка:
• Начнём с 65 человек: .
• Затем вошли 17 человек: .

Таким образом, в начале в поезде было 65 пассажиров.

В данном случае обе модели использовали очень схожий подход и пришли к верному ответу.

Приблизительное количество простых чисел

ПРОМТ: Оцените количество простых чисел, меньших, чем 10^8.

GROK-3:

Для оценки количества простых чисел, меньших , можно использовать теорему о распределении простых чисел, согласно которой количество простых чисел, не превышающих , обозначаемое как $\pi(n)$ , приближённо равно:

$\pi(n) ≈ \frac{n}{\ln(n)}$

где $\ln(n)$ натуральный логарифм числа . Для большей точности можно воспользоваться уточнённой формулой:

$\pi(n) ≈ \frac{n}{\ln(n) - 1}$

Это уточнение особенно полезно для сравнительно небольших (например, для ), так как оно корректирует небольшое завышение, свойственное упрощённой формуле.

Шаг 1: вычисление $\ln(10^8)$

$10^8 = e^{8 \ln(10)}$ , где $\ln(10) ≈ 2.302585$ .

Тогда: $\ln(10^8) = 8 × 2.302585 = 18.42068$ .

Шаг 2: применение теоремы о распределении простых чисел

Простая оценка:

$\pi(10^8) ≈ \frac{10^8}{\ln(10^8)} = \frac{10^8}{18,42068} ≈ 5428681$

Уточнённая оценка:

$\pi(10^8) ≈ \frac{10^8}{\ln(10^8) - 1} = \frac{10^8}{18,42068 - 1} = \frac{10^8}{17,42068} ≈ 5740801$

Шаг 3: сравнение с известным значением
Известно, что точное количество простых чисел, меньших , равно 5 761 455.

DEEPSEEK‑R1:

Для оценки количества простых чисел, меньших , используем теорему о распределении простых чисел, согласно которой количество простых чисел, не превышающих , приблизительно равно:

$\frac{N}{\ln(N)}$ .

При :

1. Вычислим $\ln(10^8)$ :
$\ln(10^8) = 8 \ln(10) ≈ 8 × 2,302585093 = 18,42068074$

2. Оценим количество простых чисел по теореме:

$\frac{10^8}{\ln(10^8)} ≈ \frac{100000000}{18,42068074} ≈ 5428681$

Однако эта формула даёт слегка заниженное значение. Более точную оценку можно получить с помощью логарифмического интеграла , который можно разложить в ряд:

$Li(N) ≈ \frac{N}{\ln(N)} + \frac{N}{(\ln(N))^2} + \frac{2N}{(\ln(N))^3} + \cdots$

3. Посчитаем первые несколько членов разложения:

• Первый член: $\frac{10^8}{18,42068074} ≈ 5428681$

• Второй член: $\frac{10^8}{18,42068074^2} ≈ 294705$

• Третий член: $\frac{2 × 10^8}{18,42068074^3} ≈ 32000$

• Четвёртый член: $\frac{6 × 10^8}{18,42068074^4} ≈ 5210$

4. Складываем результаты:

Известно, что точное количество простых чисел, меньших , составляет 5 761 455. Полученная с помощью логарифмического интеграла оценка оказалась очень близка к реальному значению.

Окончательный ответ
Приблизительное количество простых чисел, меньших , составляет 5 761 455.

Вердикт. Обе модели использовали корректный подход, опираясь на теорему о распределении простых чисел, однако результат DeepSeek‑r1 был ближе к реальному значению — разница около 1000, — в то время как Grok-3 ошибся примерно на 20 000. Можно сказать, что в этом раунде DeepSeek‑r1 превзошёл Grok-3.

Подсчёт гласных и возведение в степень

Эта задача определённо самая сложная для моделей. Это своеобразная вариация известной LLM‑задачи «Посчитайте количество букв R в слове „strawberry“», но с математической хитростью:

ПРОМТ: Подберите такой x для выражения (x − 14)^10, чтобы он совпадал с количеством гласных в английской словесной записи этого вычисленного выражения.

GROK-3:

Чтобы решить эту задачу, нам нужно вычислить $(x−14)^{10}$ , где — количество гласных в числительном значении ответа. Это самореференциальная задача: нужно найти такое значение , чтобы количество гласных в его словесной записи совпадало с , использованным в формуле.

Шаг 1: определим задачу
• Пусть $y = (x − 14)^{10}$ , где — количество гласных в словесной записи числа .
• Гласными считаем буквы a, e, i, o, u (для простоты только строчные буквы, если не указано иное).
• Нужно подобрать такой , чтобы количество гласных в его написании совпало с и выполнялось равенство $y = (x − 14)^{10}$ .

Шаг 2: подбор значений методом проб и ошибок
Поскольку — это количество гласных, оно должно быть неотрицательным числом: . Кроме того, $(x − 14)^{10}$ должно давать такое число, количество гласных в котором совпадает с .

Вычислим для разных значений , при этом посчитаем количество гласных в словесном представлении числа .

Случай 1:
• $y = (16 − 14)^{10} = 2^{10} = 1024$ .
• Прописываем число словами: one thousand twenty‑four.
• Считаем гласные в one thousand twenty‑four:
— o (1), e (1), o (2), u (1), a (1), o (2) → 6 гласных.
• , но в словесной записи 6 гласных. , не совпадает.

Случай 2:
• $y = (18 − 14)^{10} = 4^{10}$ .
• , следовательно $4^{10} = (4^5)^2 = 1024^2$ .
• .
• Прописываем словами: one million forty‑eight thousand five hundred seventy‑six.
• Считаем гласные:
— o (1), e (1), i (1), i (2), o (2), a (1), o (3), u (1), a (2), e (2), u (2), e (3), i (3) → 13 гласных.
• , но в словесной записи 13 гласных. , не совпадает.

Случай 3:
• $y = (15 − 14)^{10} = 1^{10} = 1$ .
• Прописываем словами: one.
• Считаем гласные в one: one → 2 гласные.
• , но в словесной записи 2 гласные. , не совпадает.

Случай 4:
• $y = (17 − 14)^{10} = 3^{10}$ .
• , следовательно $3^{10} = (3^5)^2 = 243^2$ .
• .
• Прописываем словами: fifty‑nine thousand forty‑nine.
• Считаем гласные:
— i (1), i (2), e (1), o (1), u (1), a (1), i (3), e (2) → 8 гласных.
• , но в словесной записи 8 гласных. , не совпадает.

Шаг 3: Поиск закономерностей
Подведём промежуточные итоги:
• , , гласных — 2.
• , , гласных — 2.
• , , гласных — 6.
• , , гласных — 8.
• , , гласных — 13.

Как видно, при увеличении значение растёт экспоненциально (так как возводится в 10-ю степень), а количество гласных в словесном представлении тоже увеличивается, но необязательно совпадает с .

Шаг 4: Проверка меньших значений
Теперь попробуем подобрать значения , близкие к 14, с акцентом на меньшем количестве гласных.

Случай 5:
• $y = (12 − 14)^{10} = (-2)^{10} = 1024$ .
• Записываем число словами: one thousand twenty‑four.
• Подсчёт гласных: 6 гласных (как мы уже считали ранее).
• Поскольку , а число гласных в равно 6, получаем — этот вариант не подходит.

Шаг 5: поиск фиксированной точки
Попробуем найти такой , при котором количество гласных в $(x - 14)^{10}$ совпадает с самим . Проверим , так как в предыдущих тестах малые значения гласных встречались чаще.

Случай 6:
• $y = (2 − 14)^{10} = (-12)^{10}$ .
• Так как степень чётная, $(-12)^{10} = 12^{10}$ .
• , следовательно $12^{10} = (12^5)^2 = 248 832^2$ .
• .
• Записываем словами: sixty‑one billion nine hundred seventeen million three hundred sixty‑four thousand two hundred twenty‑four.
• Подсчёт гласных:
— i (1), o (1), e (1), i (2), i (3), o (2), e (2), e (3), i (4), o (3), o (4), u (1), a (1), o (5), e (4), o (6) → всего 16 гласных.
• , но в словесной записи 16 гласных. , не совпадает.

Шаг 6: вывод
После многочисленных проверок видно, что количество гласных в $y = (x − 14)^{10}$ не совпадает с ни в одном из протестированных случаев. Это может означать, что у задачи нет решения либо поиск нужного требует специфических условий (например, другой системы обозначения чисел).

На данный момент, если необходимо дать ответ, можно сказать, что ни одно из найденных значений не удовлетворяет условиям задачи. Вероятно, требуется дополнительный анализ — возможно, с учётом альтернативных правил записи чисел или уточнения условий задачи.

DEEPSEEK‑R1:

Для вычисления $(x - 14)^{10}$ , где — это количество гласных в ответе, нужно найти такой x, при котором число гласных в словесной форме выражения $(x - 14)^{10}$ равно самому .

1. Обозначим . Тогда нам нужно подобрать так, чтобы количество гласных в словесной записи $y^{10}$ совпадало с .
2. Проверим несколько значений и посчитаем гласные в соответствующих числах, рассчитанных из выражения $(x - 14)^{10}$ .
3. Попробуем :
• $y^{10} = 4^{10} = 1048576$
• Словесная запись 1 048 576: one million forty‑eight thousand five hundred seventy‑six.
• Подсчёт гласных (A, E, I, O, U) в словесной форме числа:
— One — 2 гласные (O, E);
— Million — 3 гласные (I, O, I);
— Forty — 1 гласная (O);
— Eight — 2 гласные (E, I);
— Thousand — 3 гласные (O, U, A);
— Five — 2 гласные (I, E);
— Hundred — 2 гласные (U, E);
— Seventy — 2 гласные (E, E);
— Six — 1 гласная (I).
• Общее количество гласных: .
4. Количество гласных 18, таким образом .
5. Следовательно, $(x - 14)^{10} = (18 - 14)^{10} = 4^{10} = 1048576$ .

Вывод. DeepSeek-r1 удалось найти точное решение (ведь «двоякая» Y в английских головоломках для упрощения и единообразия считается согласной, а гласных остаётся пять: A, E, I, O, U).

Кроме того, этот вопрос удалось решить и ChatGPT‑o1 (кстати, обе модели доступны в нашем агрегаторе нейросетей):

ПРОМТ: Напишите словами значение (x − 14)^10, где x — количество гласных в ответе на этот вопрос.

CHATGPT‑O1: Sixty million four hundred sixty‑six thousand one hundred seventy‑six (шестьдесят миллионов четыреста шестьдесят шесть тысяч сто семьдесят шесть).

В ответе o1 равен 20, $(20-14)^{10}=6^{10}=6466176$ , sixty million four hundred sixty-six thousand one hundred seventy-six; буква Y тоже не учитывается.

Вердикт

Обе модели справились с первыми двумя математическими задачами, но Grok-3 потерпел неудачу в последней, которая требовала нестандартного подхода.

Программирование

Теперь мы испытаем, как эти модели проявят себя со сложной задачей с платформы LeetCode, у которой, между прочим, успешных решений всего лишь 12,8%. Вот она: «Определение первого приближённого совпадения подстроки». Упражнение было добавлено недавно, поэтому маловероятно, что модели на нём обучались.

ПРОМТ:

Даны две строки: s и pattern. Строка x называется почти равной строке y, если можно изменить не более одного символа в x, чтобы она стала идентичной y. Необходимо найти наименьший начальный индекс подстроки в s, которая является почти равной pattern. Если такой подстроки нет, вернуть -1. (Подстрока — это непрерывная последовательность символов в строке.)

Пример 1
Вход: s = "abcdefg", pattern = "bcdffg".
Выход: 1.
Объяснение. Подстрока s[1..6] == "bcdefg" может быть преобразована в "bcdffg", если изменить s[4] на "f".

Пример 2
Вход: s = "ababbababa", pattern = "bacaba".
Выход: 4.
Объяснение. Подстрока s[4..9] == "bababa" может быть преобразована в "bacaba" путём замены s[6] на "c".

Пример 3
Вход: s = "abcd", pattern = "dba".
Выход: -1.

Пример 4
Вход: s = "dde", pattern = "d".
Выход: 0.

Ограничения
• 1 <= pattern.length < s.length <= 10^5;
• s и pattern состоят только из строчных английских букв.

Ответ Grok-3

class Solution:
    def minStartingIndex(self, s: str, pattern: str) -> int:
        n = len(pattern)

        # Функция для проверки, отличаются ли две строки не более чем на один символ
        def differsByAtMostOne(s1: str, s2: str) -> bool:
            if len(s1) != len(s2):
                return False

            # Подсчёт количества различий
            diff_count = 0
            for c1, c2 in zip(s1, s2):
                if c1 != c2:
                    diff_count += 1
                if diff_count > 1:
                    return False
            return True

        # Сканируем строку s, используя скользящее окно размера n
        for i in range(len(s) - n + 1):
            # Извлекаем текущую подстроку
            substring = s[i:i+n]
            # Проверяем, отличается ли она не более чем на один символ
            if differsByAtMostOne(substring, pattern):
                return i

        return -1

Этот код действительно выполняет поставленную задачу, но на некоторых тестовых исходных данных он натолкнулся на превышение лимита времени выполнения. То есть, хотя он и решает проблему, его нельзя назвать оптимальным решением.

Ответ DeepSeek-r1

class Solution:
    def minStartingIndex(self, s: str, pattern: str) -> int:
        ans = self.find_almost_equal_substring(s, pattern)
        return ans

    def compute_z(self, s):
        n = len(s)
        Z = [0] * n
        Z[0] = 0  # Первый символ — это вся строка, но мы это не применяем
        l, r = 0, 0
        for i in range(1, n):
            if i > r:
                l = r = i
                while r < n and s[r - l] == s[r]:
                    r += 1
                Z[i] = r - l
                r -= 1
            else:
                k = i - l
                if Z[k] < r - i + 1:
                    Z[i] = Z[k]
                else:
                    l = i
                    while r < n and s[r - l] == s[r]:
                        r += 1
                    Z[i] = r - l
                    r -= 1
        return Z

    def find_almost_equal_substring(self, s, pattern):
        m = len(pattern)
        n = len(s)
        if m == 0:
            return 0
        if n < m:
            return -1

        # Шаг 1: Проверяем на точное совпадение
        exact = s.find(pattern)
        if exact != -1:
            return exact

        # Шаг 2: Вычисляем массивы lcp и lcs с использованием Z-алгоритма
        # Вычисляем lcp (наибольший общий префикс pattern, начиная с s[i])
        concat_lcp = pattern + '#' + s
        Z_lcp = self.compute_z(concat_lcp)
        lcp = [0] * n
        for i in range(n):
            lcp[i] = Z_lcp[m + 1 + i]

        # Вычисляем lcs (наибольший общий суффикс pattern,
        # заканчивающийся на s[i])
        reversed_pattern = pattern[::-1]
        reversed_s = s[::-1]
        concat_lcs = reversed_pattern + '#' + reversed_s
        Z_lcs = self.compute_z(concat_lcs)
        lcs = [0] * n
        len_rev_pat = len(reversed_pattern)
        for i in range(n):
            pos_in_rev_s = i
            pos_in_concat = len_rev_pat + 1 + pos_in_rev_s
            if pos_in_concat >= len(Z_lcs):
                lcs_val = 0
            else:
                lcs_val = Z_lcs[pos_in_concat]
            lcs[n - 1 - i] = lcs_val

        min_index = float('inf')

        # Перебираем все возможные j (позиции в pattern)
        for j in range(m):
            required_prefix = j
            required_suffix = m - j - 1

            # Перебираем возможные начальные индексы i в s
            for i in range(n - m + 1):
                # Проверяем условие для префикса
                if lcp[i] < required_prefix:
                    continue
                # Проверяем условие для суффикса
                suffix_start = i + j + 1
                if suffix_start >= n:
                    continue
                if lcs[suffix_start] < required_suffix:
                    continue
                # Проверяем, совпадает ли текущий символ
                if s[i + j] != pattern[j]:
                    if i < min_index:
                        min_index = i
                        # Выход при достижении минимального возможного индекса
                        if min_index == 0:
                            return 0
                        # Прерываем внутренний цикл, так как ищем самый ранний i
                        break

        return min_index if min_index != float('inf') else -1

Этот результат от DeepSeek‑r1 оказался неожиданным: код не прошёл даже первый тестовый случай. Если же говорить о структуре кода, то она тоже довольно неоптимальна.

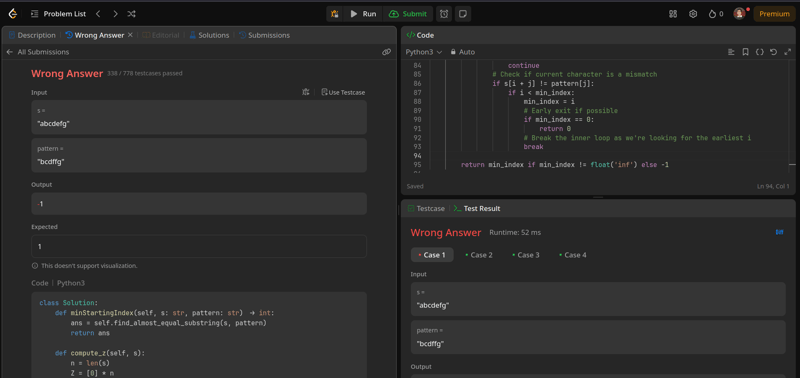
Вывод

Здесь Grok-3 однозначно выигрывает — он хотя бы выдал работающий код, пусть и не самый оптимальный. Почему‑то DeepSeek‑r1 предложил решение, которое не прошло уже первый тест и оказалось излишне длинным и плохо написанным.

Творческое письмо

ПРОМТ: Напиши рассказ на тему: «Мужчина покупает старую пишущую машинку на блошином рынке и вскоре обнаруживает, что всё, что он набирает на ней, сбывается — но с жутким подвохом». Кратко изложи сюжет, включая этот зловещий поворот, в трёх абзацах.

GROK-3:

Дэниэл Харпер, начинающий писатель, бродил по шумному блошиному рынку в промозглый осенний день в поисках вдохновения. Среди груды забытых вещей и покрытых пылью реликвий он наткнулся на старую, изящно украшенную пишущую машинку — чёрная эмаль облупилась, а клавиши пожелтели от времени. Продавец, пожилой человек с загадочной улыбкой, продал её ему всего за десять долларов, пробормотав что‑то о том, что «эта машинка живёт своей жизнью». Заинтригованный, Дэниэл принёс её домой, почистил и решил проверить, напечатав простую фразу: «Завтра я найду на улице сто долларов». На следующее утро он действительно обнаружил хрустящую купюру, лежащую в водостоке возле его дома, но едва он её поднял, как был ограблен и остался не только без денег, но и с синяком под глазом. Ошеломлённый, он начал подозревать, что машинка вовсе не обычная.

Решив испытать её силу, он напечатал: «Мой домовладелец прощает мне долг по аренде». В тот же вечер тот действительно позвонил ему, радостно сообщив, что долг списан, но на следующее утро Дэниэл узнал, что его домовладелец погиб в нелепом несчастном случае, оставив дом в хаосе. Каждое его желание сбывалось, но с пугающим и непредсказуемым изъяном. В отчаянии он попробовал написать: «Я заканчиваю роман, и он становится бестселлером», надеясь на успех. Вскоре он увидел свою книгу в продаже, однако оказалось, что она состоит из украденных текстов, из‑за чего его репутация рухнула, а на него подали в суд. Охваченный паникой, он понял, что машинка не дар, а проклятие, превращающее его желания в кошмары. Тогда он напечатал: «Я никогда не находил эту машинку», надеясь отменить её влияние, но вместо этого проснулся в реальности, где всё стало ещё хуже — он оказался бездомным, нищим и преследуемым смутными воспоминаниями о жизни, которой больше не существовало.

Охваченный страхом и не видя иного выхода, Дэниэл решил уничтожить машинку. Он разбил её молотком, затем сжёг в костре. Но на следующее утро она снова стояла на его столе, совершенно целая, будто насмехаясь над ним. Смирившись со своей судьбой, он напечатал последнее предложение: «Я свободен от проклятия этой машинки». Комната погрузилась во тьму, и он ощутил на плече ледяную руку. В следующий миг его не стало. В его опустевшей квартире, на столе, неподвижно стояла машинка. Несколько дней спустя новый жилец въехал в квартиру, обнаружил старинное устройство и, заинтригованный, набрал первую фразу, не зная, что только что запустил тот же самый роковой цикл. История заканчивается тем, что проклятие машинки продолжается и всякий, кто осмелится её использовать, становится жертвой своих же желаний.

DEEPSEEK‑R1:

Итан Рид, начинающий писатель, находит на блошином рынке ржавую пишущую машинку Underwood 1930-х годов, почувствовав её зловещую ауру. Дома он решает проверить её в действии: набирает «Передо мной появляется свежая чашка кофе» — и с изумлением наблюдает, как она действительно материализуется. Но радость быстро сменяется болью: горячая жидкость выплёскивается и обжигает ему руку, словно предупреждая о коварной логике машинки. Несмотря на ожог, Итан не может устоять перед искушением. Он осторожно продолжает эксперименты, печатая мелкие желания, которые оборачиваются неприятными последствиями: стодолларовая купюра оказывается заляпанной кровью, а починенный кран выходит из строя и затапливает его квартиру. Машинка исполняет просьбы, но с мрачным, злобным изъяном.

Одержимый отчаянием, Итан решается на более серьёзные перемены. Он набирает: «Меня повышают» — и вскоре получает долгожданное повышение, но узнаёт, что его коварного начальника подставили и обвинили в хищении средств, оставив Итана мучиться чувством вины. Когда его пожилая соседка миссис Кларк тяжело заболевает, он пишет: «Миссис Кларк исцелена» — и она действительно чудесным образом выздоравливает... но тут же становится навязчиво одержимой им, преследуя его день и ночь. Его последняя попытка обрести богатство вызывает появление чемодана с деньгами, но вскоре выясняется, что это деньги наркокартеля, и полиция выходит на его след. Каждое желание лишь сильнее разрушает его жизнь, а проклятие машинки становится всё опаснее с каждым новым напечатанным словом.

Охваченный паникой, Итан пытается вернуть всё назад, печатая: «Пусть всё станет как было». Мир начинает искажаться: его квартира возвращается в прежнее состояние, миссис Кларк исчезает, деньги испаряются. Но машинка требует жертву — его самого. Итан приходит в себя в сером, безжизненном пространстве, перед ним всё та же машинка, клавиши которой сами по себе выбивают: «Итана Рида никогда не существовало». Он навечно застрял в этом лимбе, наблюдая, как машинка снова появляется на прилавке блошиного рынка в ожидании следующей жертвы. Финальная сцена: продавец с пыльного лотка ухмыляется и шепчет: «Продано... очередной отчаявшейся душе», — и проклятие продолжается.

Итак, несмотря на то что DeepSeek‑r1 считается лучшей моделью для художественного письма...

...в данном случае обе модели отлично постарались с созданием истории и сумели гармонично вплести в неё зловещий поворот всего в трёх абзацах.

Что в итоге?

Разбирая возможности Grok-3 и DeepSeek‑r1, можно сказать, что обе модели показали достойные результаты: Grok-3 впечатлил своей логической последовательностью и умением анализировать сложные сценарии, а DeepSeek‑r1 оказался точнее в математических вычислениях. Однако, когда речь зашла о программировании, Grok-3 оказался впереди, предложив хотя бы работоспособное, пусть и неоптимальное решение. В творческом письме же оба ИИ продемонстрировали умение рассказывать захватывающие истории, но без явного победителя.

Если взглянуть шире, эта дуэль напоминает классическое противостояние подходов к развитию технологий: Grok-3 — типичный представитель закрытых мощных моделей, созданных в духе «чем больше данных и ресурсов, тем лучше», а DeepSeek‑r1, напротив, продолжает традицию открытых разработок, где сообщество может не просто пользоваться инструментом, но и изменять его.

Благодарю за прочтение (‑: А что вы думаете, чья стратегия вам кажется выигрышной?

Теги:

Хабы: