McKenzy 19 апр 2018 в 14:09

Ассоциативные правила, или пиво с подгузниками

19 мин

77K

Блог компании Open Data SciencePython*R*Алгоритмы*Машинное обучение*

Введение в теорию

Обучение на ассоциативных правилах (далее Associations rules learning — ARL) представляет из себя, с одной стороны, простой, с другой — довольно часто применимый в реальной жизни метод поиска взаимосвязей (ассоциаций) в датасетах, или, если точнее, айтемсетах (itemsests). Впервые подробно об этом заговорил Piatesky-Shapiro G [1] в работе “Discovery, Analysis, and Presentation of Strong Rules.” (1991) Более подробно тему развивали Agrawal R, Imielinski T, Swami A в работах “Mining Association Rules between Sets of Items in Large Databases” (1993) [2] и “Fast Algorithms for Mining Association Rules.” (1994) [3].

В общем виде ARL можно описать как «Кто купил x, также купил y». В основе лежит анализ транзакций, внутри каждой из которых лежит свой уникальный itemset из набора items. При помощи ARL алогритмов находятся те самые «правила» совпадения items внутри одной транзакции, которые потом сортируются по их силе. Все, в общем, просто.

За этой простотой, однако, могут скрываться поразительные вещи, о которых common sense даже не подозревал.

Классический случай такого когнитивного диссонанса описан в статье D.J. Power «Ask Dan!», опубликованной в DSSResources.com [4].

В 1992 году группа по консалтингу в области ритейла компании Teradata под руководством Томаса Блишока провела исследование 1.2 миллиона транзакций в 25 магазинах для ритейлера Osco Drug (нет, там продавали не наркотики и даже не лекарства, точнее, не только лекартсва. Drug Store — формат разнокалиберных магазинов у дома). После анализа всех этих транзакций самым сильным правилом получилось «Между 17:00 и 19:00 чаще всего пиво и подгузники покупают вместе». К сожалению такое правило показалось руководству Osco Drug настолько контринтуитивным, что ставить подгузники на полках рядом с пивом они не стали. Хотя объяснение паре пиво-подгузники вполне себе нашлось: когда оба члена молодой семьи возвращались с работы домой (как раз часам к 5 вечера), жены обычно отправляли мужей за подгузниками в ближайший магазин. И мужья, не долго думая, совмещали приятное с полезным — покупали подгузники по заданию жены и пиво для собственного вечернего времяпрепровождения.

Описание Association rule

Итак, мы выяснили, что пиво и подгузники — хороший джентльменский набор, а что дальше?
Пусть у нас имеется некий датасет (или коллекция) D, такой, что $D = {d_0 ... d_j}$ , где d — уникальная транзакция-itemset (например, кассовый чек). Внутри каждой d представлен набор items (i — item), причем в идеальном случае он представлен в бинарном виде: d1 = [{Пиво: 1}, {Вода: 0}, {Кола: 1}, {...}], d2 = [{Пиво: 0}, {Вода: 1}, {Кола: 1}, {...}]. Принято каждый itemset описывать через количество ненулевых значений (k-itemset), например, [{Пиво: 1}, {Вода: 0}, {Кола: 1}] является 2-itemset.

Если изначально датасет в бинарном виде не представлен, можно при желании руками его преобразовать (One Hot Encoding и pd.get_dummies вам в помощь).

Таким образом, датасет представляет собой разреженную матрицу со значениями {1,0}. Это будет бинарный датасет. Существуют и другие виды записи — вертикальный датасет (показывает для каждого отдельного item вектор транзакций, где он присутствует) и транзакционный датасет (примерно как в кассовом чеке).

ОК, данные преобразовали, как найти правила?
Существует целый ряд ключевых (если хотите — базовых) понятий в ARL, которые нам помогут эти правила вывести.

Support (поддержка)

Первое понятие в ARL — support:

$supp(X) = \frac{\{t\in T;\ X \in t\}}{|T|}$

, где X — itemset, содержащий в себе i-items, а T — количество транзакций. Т.е. в общем виде это показатель «частотности» данного itemset во всех анализируемых транзакциях. Но это касается только X. Нам же интересен скорее вариант, когда у нас в одном itemset встречаются x1 и x2 (например). Ну тут тоже все просто. Пусть x1 = {Пиво}, а x2 = {Подгузники}, значит нам нужно посчитать, во скольких транзакциях встречается эта парочка.

$supp(x_1\cup x_2) = \frac{\sigma(x_1 \cup x_2)}{|T|}$

где $\sigma$ — количество транзакций, содержащих $inline$ и $inline$
Разберемся с этим понятием на игрушечном датасете.

play_set # микродатасет, где указаны номера транзакций, а также в бинарном виде представлено, что покупалось на каждой транзакции

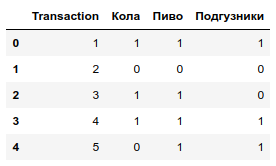
$supp = \frac{\text{Транзакции с пивом и подгузниками}}{\text{Все транзакции}}= P(\text{Пиво}\cap\text{Подгузники})$

$supp = \frac{3}{5} = 60\%$

Confidence (достоверность)

Следующее ключевое понятие — confidence. Это показатель того, как часто наше правило срабатывает для всего датасета.

$conf(x_1\cup x_2) = \frac{supp(x_1 \cup x_2)}{supp(x_1)}$

Приведем пример: мы хотим посчитать confidence для правила «кто покупает пиво, тот покупает и подгузники».

Для этого сначала посчитаем, какой support у правила «покупает пиво», потом посчитаем support у правила «покупает пиво и подгузники», и просто поделим одно на другое. Т.е. мы посчитаем в скольких случаях (транзакциях) срабатывает правило «купил пиво» supp(X), «купил подгузники и пиво»

$supp(X \cup Y)$

Ничего не напоминает? Байес смотрит на все это несколько недоуменно и с презрением.

Посмотрим на нашем микродатасете.

$conf(\text{Пиво}\cup \text{Подгузники}) = \frac{supp(\text{Пиво}\cup \text{Подгузники})}{supp(\text{Пиво})} = P(\text{Подгузники}\mid\text{Пиво})$

$conf = \frac{3}{4}= 75\%$

Lift (поддержка)

Следующее понятие в нашем списке — lift. Грубо говоря, lift — это отношение «зависимости» items к их «независимости». Lift показывает, насколько items зависят друг от друга. Это очевидно из формулы:

$lift(x_1\cup x_2) = \frac{supp(x_1 \cup x_2)}{supp(x_1) \times supp(x_2)}$

Например, мы хотим понять зависимость покупки пива и покупки подгузников. Для этого считаем support правила «купил пиво и подгузники» и делим его на произведение правил «купил пиво» и «купил подгузники». В случае, если lift = 1, мы говорим, что items независимы и правил совместной покупки тут нет. Если же lift > 1, то величина, на которую lift, собственно, больше этой самой единицы, и покажет нам «силу» правила. Чем больше единицы, тем круче. Если lift < 1, то это покажет, что правило основания $x_2$ негативно влияет на правило $x_1$. По-другому lift можно определить как отношение confidence к expected confidence, т.е. отношение достоверности правила, когда оба (ну или сколько там захотите) элемента покупаются вместе к достоверности правила, когда один из элементов покупался (неважно, со вторым или без).

$lift = \frac{\text{Confidence}}{\text{Expected confidence}} = \frac{P(\text{Подгузники} \mid \text{Пиво})}{P(\text{Подгузники})}$

$lift = \frac{\frac{3}{4}}{\frac{3}{5}} = 1,25$

Т.е. наше правило, что пиво покупают с подгузникми, на 25% мощнее правила, что подгузники просто покупают

Conviction (убедительность)

В общем виде Conviction — это «частотность ошибок» нашего правила. Т.е., например, как часто покупали пиво без подгузников и наоборот.

$conv(x_1\cup x_2) = \frac{1 - supp(x_2)}{1 - conf(x_1 \cup x_2)}$

$conv(\text{Пиво}\cup \text{Подгузники} ) = \frac{1 - supp(\text{Подгузники})}{1 - conf(\text{Пиво} \cup \text{Подгузники})} = \frac{1 - 0.6}{1 - 0.75} = 1,6$

Чем результат по формуле выше 1, тем лучше. Например, если conviction покупки пива и подгузников вместе был бы равен 1.2, это значит, что правило «купил пиво и подгузники» было бы в 1.2 раза (на 20%) более верным, чем если бы совпадение этих items в одной транзакции было бы чисто случайным. Немного не интуитивное понятие, но оно и используется не так часто, как предыдущие три.

Существует ряд часто используемых классических алгоритмов, позволяющих находить правила в itemsets согласно перечисленным выше понятиям — Наивный или брутфорс-алгоритм, Apriori- алгоритм, ECLAT-алгоритм, FP-growth алгоритм и другие.

Брутфорс

Найти правила в itemsets в общем не сложно, сложно сделать это эффективно. Брутфорс-алгоритм самый простой и, в то же время, самый неэффективный способ.

В псевдо-коде алгоритм выглядит так:

ВХОД: Датасет D, содержащий список транзакций
ВЫХОД: Наборы itemsets $inline$ где $inline$ — набор itemsets размера I, которые встречаются как минимум s раз в D
ПОДХОД:

1. R — целочисленный array, содержащий в себе все комбинации items в D, размера $2^{|D|}$
2. for n $\in$ [1, |D|] do:
F — все возможные комбинации из $inline$
Увеличить каждое значение в R согласно значениям в каждом F[]
3. return Все itemsets в R $\geq$ s

Сложность брутфорс-алгоритма очевидна:

Для того чтобы найти все возможные Association rules применяя брутфорс-алгоритм нам необходимо перечислить все подмножества X из набора I и для каждого подмножества X рассчитать supp(X). Данный подход будет состоять из следующих шагов:

генерация кандидатов. Данный шаг состоит из перебора всех возможных подмножеств X подмножества I. Данные подмножества называются кандидатами, поскольку каждое подмножество теоретически может являться часто встречаемым подмножеством, то множество потенциальных кандидатов будет состоять из
$2^{|D|}$
элементов (здесь |D| обозначается число элементов множества I, а
$2^{|D|}$
часто называется булеаном множества I, то есть множество всех подмножеств I)
расчет support. На данном шаге рассчитывается supp(X) каждого кандидата X

Таким образом, сложность нашего алгоритма будет:

$O(|I|*|D|*2^{|I|})$

, где

$O(2^{|I|})$

— количество возможных кандидатов

$display$

— сложность расчета supp(X), поскольку для расчета supp(X) нам необходимо перебрать все элементы в I в каждой транзакции

$t \in T$

В нотации O-большое нам понадобится O(N) операций, где N — количество itemsets.
Таким образом, для применения брутфорс-алгоритма нам понадобится $inline$ ячеек памяти, где i — индивидуальный itemset. Т.е. для хранения и обсчета 34 items нам понадобится 128GB RAM (для 64-битных целочисленных ячеек).

Таким образом брутфорс поможет нам в обсчете транзакций в палатке с шаурмой у вокзала, но для чего-то более серьезного он совершенно не пригоден.

Apriori Algorithm

Теория

Используемые понятия:

Множество объектов (itemset):
$X \subseteq I = \{x_1, x_2, ..., x_n\}$
Множество идентификаторов транзакций (tidset):
$T = \{t_1, t_2, ..., t_m\}$
Множество транзакций (transactions):
$\{(t,\ X):\ t\in T,\ X \in I\}$

Введем дополнительно еще несколько понятий.

Будем рассматривать дерево префиксов (prefix tree), где 2 элемента X и Y соединены, если X является прямым подмножеством Y. Таким образом мы можем пронумеровать все подмножества множества I. Рисунок приведен ниже:

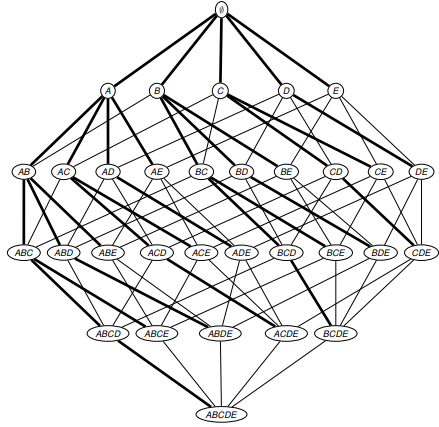
Итак, рассмотрим алгоритм Apriori.

Apriori использует следующее утверждение: если $X \subseteq Y$ , то $supp(X) \geq supp(Y)$ .

Отсюда следуют следующие 2 свойства:

если Y встречается часто, то любое подмножество
$X: X \subseteq Y$
так же встречается часто
если X встречается редко, то любое супермножество
$Y: Y \supseteq X$
так же встречается редко

Apriori алгоритм по-уровнево проходит по префиксному дереву и рассчитывает частоту встречаемости подмножеств X в D. Таким образом, в соответствии с алгоритмом:

исключаются редкие подмножества и все их супермножества
рассчитывается supp(X) для каждого подходящего кандидата X размера k на уровне k

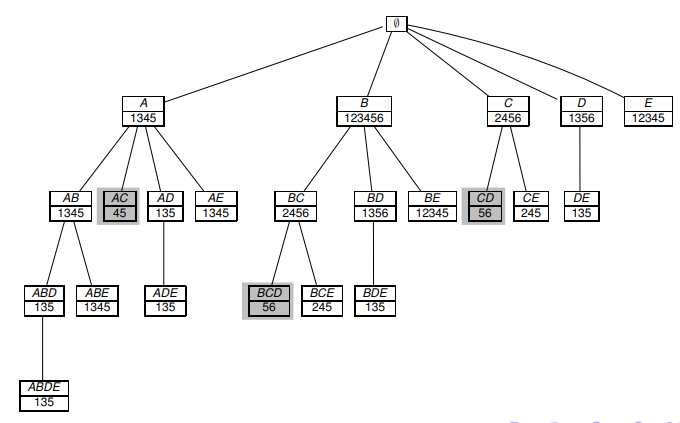
В псевдо-код нотации Априори-алгоритм выглядит следующим образом:
ВХОД: Датасет D, содержащий список транзакций, и $\sigma$ — задаваемый пользователем порог supp

ВЫХОД: Список itemsets F(D, $\sigma$ )

ПОДХОД:

1. $C_1 \leftarrow$ [{i}|i in J]
2. k $\leftarrow$ 1
3. while $C_k \neq$ 1 do:
4. Считаем все support для всех кандидатов
for all транзакций (tid, I) $\in$ D do:
for all кандидатов X $\in$ $inline$ do:
if X $\in$ I:
X.support++
5. #Вытаскиваем все частые itemsets:
$inline$ = {X|X.support > $\sigma$ }
6. #Генерируем новых кандидатов
$\forall$ X,Y $\in$ $inline$ , X[i] = Y[i] for 1 $\leq$ i $\leq$ k-1 and X[k] $\leq$ Y[k] do:
I = X $\cup$ {Y|k|}
if $\forall$ J $\subseteq$ I,|J| = k: J $\in$ $inline$ then
$inline$ $\in$ $inline$ $\cup$ I
k++

Таким образом, Apriori сначала ищет все единичные (содержащие 1 элемент) itemsets, удовлетворяющие заданному пользователем supp, затем составляет из них пары по принципу иерархической монотонности, т.е. если $inline$ встречается часто и $inline$ встречается часто, то и $inline$ встречается часто.

Явным минусом такого подхода является то, что необходимо «просканировать» весь датасет, посчитать все supp на всех уровнях breadth-first search (поиск в ширину)
Это также может подъесть RAM на больших датасетах, хотя алгоритм в плане скорости все равно намного эффективнее брутфорса.

Реализация в Python

from sklearn import… эммм… а импортировать-то и нечего. На данный момент модулей для ALR в sklearn нет. Ну ничего, погуглим или напишем свои, правда?

По сети гуляет целый ряд реализаций, например [вот], [вот], и даже [вот].

Мы же на практике придерживаемся алгоритма apyori, написанного Ю Мочизуки (Yu Mochizuki). Полный код приводить не будем, желающие могут посмотреть [тут], а вот архитектуру решения и пример использования покажем.

Условно решение Мочизуки можно разделить на 4 части: Структура данных, Внутренние функции, API и Прикладные функции.

Первая часть модуля (Структура данных) работает с изначальным датасетом. Реализуется класс TransactionManager, методы которого объединяют транзакции в матрицу, формируют список правил-кандидатов и считают support для каждого правила. Внутренние функции дополнительно по support'у формируют списки правил и соответственно их ранжируют. API логично позволяет работать напрямую с датасетами, а Прикладные функции позволяют обрабатывать транзакции и выводить результат в читаемый вид. Никакого rocketscience.

Посмотрим, как использовать модуль на реальном (ну, в данном случае — игрушечном) датасете.

Подгрузка данных

import pandas as pd
# загрузим данные
dataset = pd.read_csv('data/Market_Basket_Optimisation.csv', header = None)
# посомтрим на датасет
dataset.head()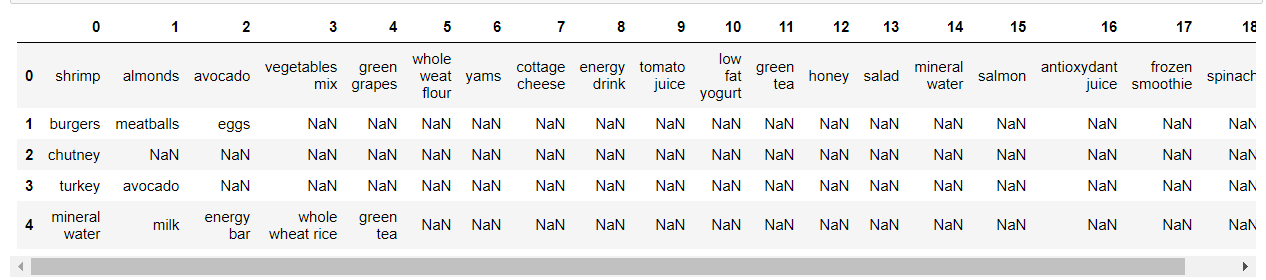

Видим, что датасет у нас представляет разреженную матрицу, где в строках у нас набор items в каждой транзакции.

Заменим NaN на последнее значение внутри транзакции, чтобы потом было легче обрабатывать весь датасет.

Код

dataset.fillna(method = 'ffill',axis = 1, inplace = True)
dataset.head()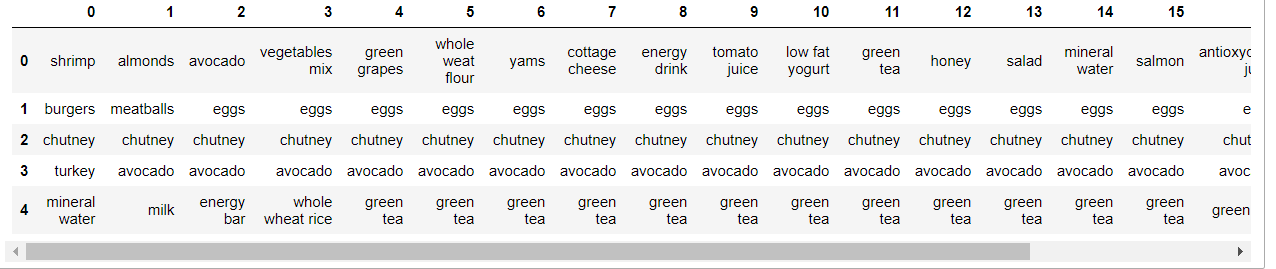

#создаим из них матрицу
transactions = []
for i in range(0, 7501): 
    transactions.append([str(dataset.values[i,j]) for j in range(0, 20)])
#загружаем apriori
import apriori
%%time
# и обучимся правилам. Обратите внимание, что пороговые значения мы вибираем сами в зависимости от того,
# насколкьо "сильные" правила мы хотим получить
# min_support -- минимальный support для правил (dtype = float).
# min_confidence -- минимальное значение confidence для правил (dtype = float)
# min_lift -- минимальный lift (dtype = float)
# max_length -- максимальная длина itemset (вспоминаем про k-itemset)  (dtype = integer)

result = list(apriori.apriori(transactions, min_support = 0.003, min_confidence = 0.2, min_lift = 4, min_length = 2))

Визуализируем выход

Кодомагия

import shutil, os 
try:
    from StringIO import StringIO
except ImportError:
    from io import StringIO
import json #преобразовывать будем в json, используя встроенные в модуль методы
output = []
for RelationRecord in result:
    o = StringIO()
    apriori.dump_as_json(RelationRecord, o)
    output.append(json.loads(o.getvalue()))
data_df = pd.DataFrame(output)
# и взгялнем на итоги
pd.set_option('display.max_colwidth', -1)

from IPython.display import display, HTML

display(HTML(data_df.to_html()))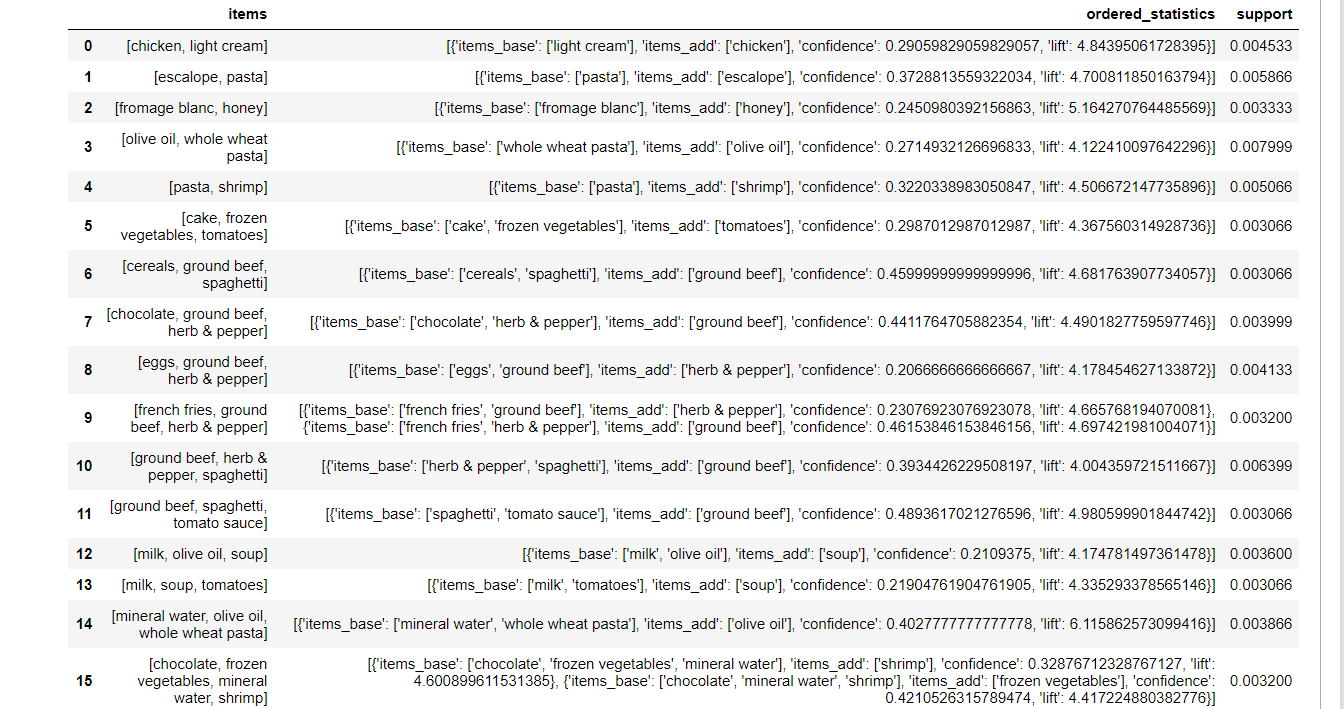

Итого мы видим:

1. Пары items
2. items_base — первый элемент пары
3. items_add — второй (добавленный алгоритмом) элемент пары
4. confidence — значение confidence для пары
5. lift — значение lift для пары
6. support — значение support для пары. При желании, по нему можно отсортировать

Результаты логичные: эскалоп и макароны, эскалоп и сливочно-грибной соус, курица и нежирная сметана, мягкий сыр и мед и т.д. — все это вполне логичные и, главное, вкусные сочетания.

Реализация в R

ARL тот случай, когда R-филы могут злорадно похихикать (java-филы вообще смотрят на нас смертных с презрением, но об этом ниже). В R реализована библиотека arules, где присутствует и apriori, и другие алгоритмы. Официальную доку можно посмотреть [тут]

Посмотрим на нее в действии:

Для начала установим ее (если еще не установили).

Установка библиотеки

install.packages('arules')

Считаем данные и преобразуем их в матрицу транзакций.

Читаем данные

library(arules)
dataset = read.csv('Market_Basket_Optimisation.csv', header = FALSE)
dataset = read.transactions('Market_Basket_Optimisation.csv', sep = ',', rm.duplicates = TRUE)

Посмотрим на данные:

summary(dataset)
itemFrequencyPlot(dataset, topN = 10)

На графике представлена частотность отдельныйх items в транзакциях.

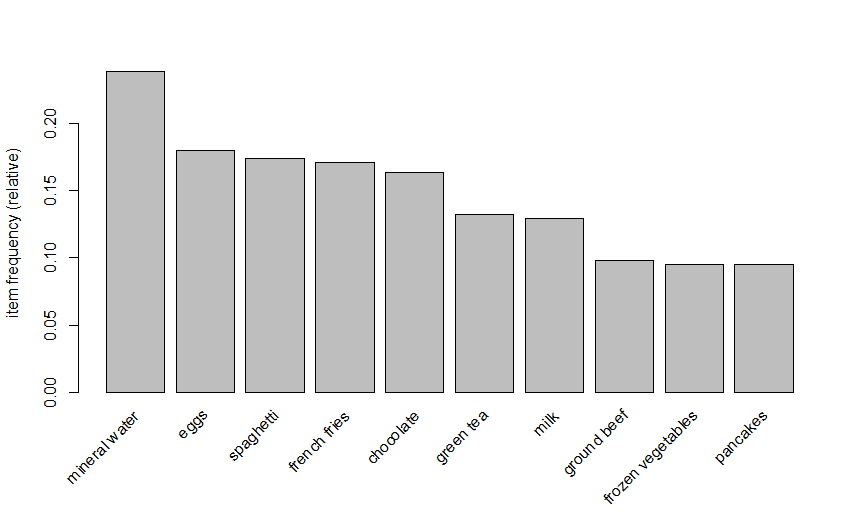
Выучим наши правила:

В общем виде функция вызова apriori выглядит так:

apriori(data, parameter = NULL, appearance = NULL, control = NULL)

, где

data — наш датасет
parameter — список (list) параметров для модели: минимальные support, confidence и lift
appearance — отвечает за отображение данных. Может принимать значения lhs, rhs, both, items, none, которые определяют положение items в output
control — отвечает за сортировку вывода (ascending, descending, без сортировки), а также за то, отображать ли прогрессбар или нет (параметр verbose)

Обучим модель:

rules = apriori(data = dataset, parameter = list(support = 0.004, confidence = 0.2))

И посмотрим на результаты:

inspect(sort(rules, by = 'lift')[1:10])

Убедимся, что на выходе имеем примерно те же результаты, что при использовании модуля apyori в Python:

1. {light cream} => {chicken} 0.004532729
2. {pasta} => {escalope} 0.005865885
3. {pasta} => {shrimp} 0.005065991
4. {eggs,ground beef} => {herb & pepper} 0.004132782
5. {whole wheat pasta} => {olive oil} 0.007998933
6. {herb & pepper,spaghetti} => {ground beef} 0.006399147
7. {herb & pepper,mineral water} => {ground beef} 0.006665778
8. {tomato sauce} => {ground beef} 0.005332622
9. {mushroom cream sauce} => {escalope} 0.005732569
10. {frozen vegetables,mineral water,spaghetti} => {ground beef} 0.004399413

ECLAT Algorithm

Теория

Идея алгоритма ECLAT (Equivalence CLAss Transformation) заключается в ускорении подсчета supp(X). Для этого нам необходимо проиндексировать нашу базу данных D так, чтобы это позволило быстро рассчитывать supp(X)

Легко заметить, что если t(X) обозначает множество всех транзакций, где встречается подмножество X, то
t(XY) = t(X) $\cup$ t(Y)
и
supp(XY) = |t(XY)|
то есть supp(XY) равен кардинальности (размеру) множества t(XY)

Данный подход может быть значительно усовершенствован путем уменьшения размера промежуточных множеств идентификаторов транзакций (tidsets). А именно, мы можем хранить не все множество транзакций на промежуточном уровне, а только множество различий этих транзакций. Предположим, что

$X_a = \{x_1, x_2,..., x_{n-1}, a\} X_b = \{x_1, x_2,..., x_{n-1}, b\}$

Тогда, мы получим:

$X_{ab} = \{x_1, x_2,..., x_{n-1}, a, b\}$

$diffset(X_{ab})$ это множество всех id транзакций, которые содержат префикс X_a, но не содержат элемент b:

$d(X_{ab}) =t(X_a)/t(X_{ab})=t(X_a)/t(X_{b})$

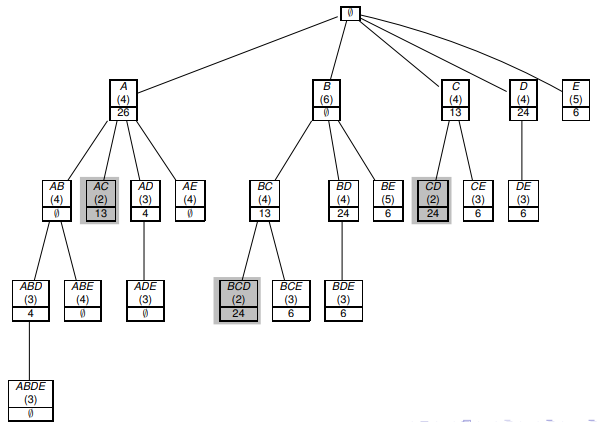
В отличие от Apriori-алгоритма, ECLAT производит поиск в глубину (DFS, [подробнее тут]). Иногда его называют «вертикальным» (в отличие от «горизонтального» для Apriori)

ВХОД: Датасет D, содержащий список транзакций, $\sigma$ — задаваемый пользователем порог supp и новый элемент префикс $I \subseteq J$

ВЫХОД: Список itemsets F[I](D, $\sigma$ ) для соответствующего префикса I

ПОДХОД:
1. $F[i] \leftarrow$ {}
2. $\forall$ i $\in$ J $\in$ D do:
F[I] := F[I] $\in$ {I $\in$ {i}}
3. Создаем $inline$
$D_i \leftarrow$ {}
$\forall$ j $\in$ J $\in$ D $\in$ j > i do:
C $\cup$ ({i} $\cup$ {j})
if |C| $\geq \sigma$ then
$D_i \leftarrow D_i \in {C,i}$
4. DFS — рекурсия:
Считаем $F|I| \in {i}| (D_i, \sigma)$
F[I]: F[I] $\in$ F[I $\in$ i]

Ключевым понятием для ECLAT-алгоритма является I-префикс. В начале генерируется пустое множество I, это позволяет нам на первом проходе выделить все частотные itemsets. Затем алгоритм будет вызывать сам себя и увеличивать I на 1 на каждом шаге до тех пор, пока не будет достигнута заданная пользователем длина I.

Для хранения значений используется префиксное дерево (trie (не tree:)), [тут подробнее]. Вначале строится нулевой корень дерева (то самое пустое множество I), затем по мере прохода по itemsets алгоритм прописывает содержащиеся в каждом itesmsets items, при этом самая левая ветвь является child нулевого корня и далее вниз. При этом ветвей столько, сколько items встречается в itemsets. Такой подход позволяет записывать itemset в памяти только один раз, что делает ECLAT быстрее Apriori.

Реализация в Python

Существует несколько реализаций данного алгоритма в Python, желающие могут погуглить и даже попытаться их заставить работать, но мы же напишем свой, максимально простой и, главное, рабочий.

import numpy as np
"""
Класс инициируется 3мя параметрами:
- min_supp - минимальный support  который мы рассматриваем для ItemSet. Рассчитывается как % от количества транзакций
- max_items - максимальное количество елементов в нашем ItemSet
- min_items - минимальное количество элементов ItemSet
"""
class Eclat:
    #инициализация объекта класса
    def __init__(self, min_support = 0.01, max_items = 5, min_items = 2):
        self.min_support = min_support
        self.max_items = max_items
        self.min_items = min_items
        self.item_lst = list()
        self.item_len = 0
        self.item_dict = dict()
        self.final_dict = dict()
        self.data_size = 0
    
    #создание словаря из ненулевых объектов из всех транзакций (вертикальный датасет)
    def read_data(self, dataset):
        for index, row in dataset.iterrows():
            row_wo_na = set(row[0])
            for item in row_wo_na:
                item = item.strip()
                if item in self.item_dict:
                    self.item_dict[item][0] += 1
                else:
                    self.item_dict.setdefault(item, []).append(1)
                self.item_dict[item].append(index)
        #задаем переменные экземпляра (instance variables)
        self.data_size = dataset.shape[0]
        self.item_lst = list(self.item_dict.keys())
        self.item_len = len(self.item_lst)
        self.min_support = self.min_support * self.data_size
        #print ("min_supp", self.min_support)
        
    #рекурсивный метод для поиска всех ItemSet по алгоритму Eclat
    #структура данных: {Item: [Supp number, tid1, tid2, tid3, ...]}
    def recur_eclat(self, item_name, tids_array, minsupp, num_items, k_start):
        if tids_array[0] >= minsupp and num_items <= self.max_items:
            for k in range(k_start+1, self.item_len):
                if self.item_dict[self.item_lst[k]][0] >= minsupp:
                    new_item = item_name + " | " + self.item_lst[k]
                    new_tids = np.intersect1d(tids_array[1:], self.item_dict[self.item_lst[k]][1:])
                    new_tids_size = new_tids.size
                    new_tids = np.insert(new_tids, 0, new_tids_size)
                    if new_tids_size >= minsupp:
                        if num_items >= self.min_items: self.final_dict.update({new_item: new_tids})
                        self.recur_eclat(new_item, new_tids, minsupp, num_items+1, k)
    
    #последовательный вызов функций определенных выше
    def fit(self, dataset):
        i = 0
        self.read_data(dataset)
        for w in self.item_lst:
            self.recur_eclat(w, self.item_dict[w], self.min_support, 2, i)
            i+=1
        return self
        
    #вывод в форме словаря {ItemSet: support(ItemSet)}
    def transform(self):
        return {k: "{0:.4f}%".format((v[0]+0.0)/self.data_size*100) for k, v in self.final_dict.items()}

Потестируем на игрушечной выборке:

#создадим экземпляр класса с нужными нам параметрами
model = Eclat(min_support = 0.01, max_items = 4, min_items = 3)

#обучим
model.fit(dataset)

#и визуализируем результаты
model.transform()

Meanwhile in real-life...

Итак, алгоритм работает. Но так ли он применим в реальной жизни? Давайте проверим.
Есть реальная бизнес задача, которая поступила нам от крупного продуктового ритейлера премиум-сегмента (раскрывать название и наименования товаров не будем, корпоративная тайна-с): посмотреть те самые наиболее частые наборы в продуктовых корзинах.

Загрузим данные из выгрузки из POS-ситемы (Point-of-Sale — система, обрабатывающая транзакции на кассах)

Загрузка данных

df = pd.read_csv('data/tranprod1.csv', delimiter = ';', header = 0)
df.columns = ['trans', 'item']
print(df.shape)
df.head()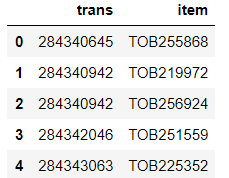

Поменяем формат таблицы на «транзакция | список» всех item в транзакции

Трансформации

df.trans = pd.to_numeric(df.trans, errors='coerce')
df.dropna(axis = 0, how = 'all', inplace = True)
df.trans = df.trans.astype(int)

df = df.groupby('trans').agg(lambda x: x.tolist())

df.head()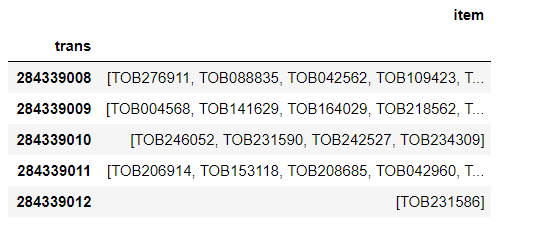

Запустим алгоритм

model = Eclat(min_support = 0.0001, max_items = 4, min_items = 3)

%%time
model.fit(df)

Data read successfully

min_supp 9.755

CPU times: user 6h 47min 9s, sys: 22.2 s, total: 6h 47min 31s

Wall time: 6h 47min 28s

model.transform()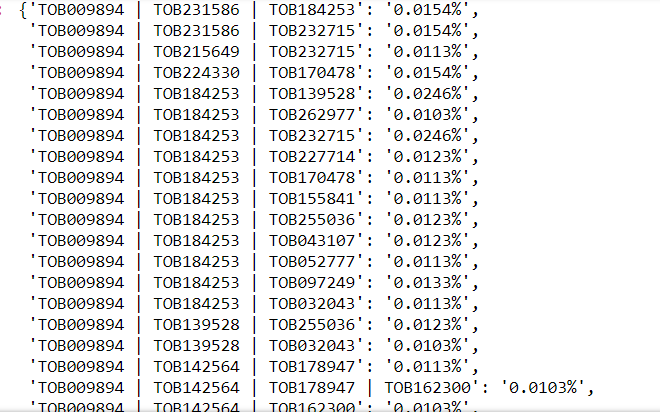

На обычном компьютере решение этой задачки заняло по сути ночь. На cloud-платформах было бы быстрее. Но, главное, клиент доволен.

Как видно, реализовать алгоритм своими силами довольно просто, хотя с эффективностью стоит поработать.

Реализация в R
И вновь пользователи R ликуют, для них никаких танцев с бубном делать не надо, все по аналогии с apriori.

Запускаем библиотеку и читаем данные (для ускорения возьмем тот же игрушечный датасет, на котором считали apriori):

Подготовка данных

library(arules)
dataset = read.csv('Market_Basket_Optimisation.csv')
dataset = read.transactions('Market_Basket_Optimisation.csv', sep = ',', rm.duplicates = TRUE)

Быстрый взгляд на датасет:

summary(dataset)
itemFrequencyPlot(dataset, topN = 10)

Те же частоты, что и до этого

Правила:

rules = eclat(data = dataset, parameter = list(support = 0.003, minlen = 2))

Обратите внимание, настраиваем только support и минимальную длину (k в k-itemset)

И смотрим на результаты:

inspect(sort(rules, by = 'support')[1:10])

FP-Growth Algorithm

Теория

FP-Growth (Frequent Pattern Growth) алгоритм самый молодой из нашей троицы, впервые он описан в 2000 году в [7].

FP-Growth предлагает радикальную вещь — отказаться от генерации кандидатов (напомним, генерация кандидатов лежит в основе Apriori и ECLAT). Теоретически, такой подход позволит еще больше увеличить скорость алгоритма и использовать еще меньше памяти.

Это достигается за счет хранения в памяти префиксного дерева (trie) не из комбинаций кандидатов, а из самих транзакций.

При этом FP-Growth генерирует таблицу заголовков для каждого item, чей supp выше заданного пользователем. Эта таблица заголовков хранит связанный список всех однотипных узлов префиксного дерева. Таким образом, алгоритм сочетает в себе плюсы BFS за счет таблицы заголовков и DFS за счет построения trie. Псевдокод алгоритма схож с ECALT, за некоторыми исключениями.

ВХОД: Датасет D, содержащий список транзакций, $\sigma$ — задаваемый пользователем порог supp и префикс $I \subseteq J$

ВЫХОД: Список itemsets F[I](D, $\sigma$ ) для соответствующего префикса I

ПОДХОД:

1. F[i] $\leftarrow$ {}
2. $\forall$ i $\in$ J $\in$ D do:
F[I] := F[I] $\in$ {I $\in$ {i}}
3. Создаем $inline$
$D_i \leftarrow D_i$ {}
$H_i \leftarrow$ {}
$\forall$ j $\in$ J $\in$ D $\in$ j > i do:
if supp (I $\in$ {i,j}) $\geq \sigma$ then:
H $\leftarrow$ H $\in$ {j}
$\forall$ (tid, X) $\in$ D $\subseteq$ I $\in$ X do:
$D_i \leftarrow D_i$ $\subseteq$ ({tid,X $\in$ H})
4. DFS — рекурсия:
Считаем F|I $\in$ {i}| ( $D_i, \sigma$ )
F[I] $\leftarrow$ F[I] $\subseteq$ F[I $\subseteq$ i]

Реализация в Python

Реализации FP-Growth в Питоне повезло не больше, чем другим ALR-алгоритмам. Стандартных библиотек под него нет.

Неплохо FP_Growth представлен в pyspark, смотреть [тут]
На gitHub тоже можно найти несколько решений эпохи неолита, например [тут] и [тут]

Потестим второй вариант:

Установка и импорт

!pip install pyfpgrowth

import pyfpgrowth

#Сгенериуем паттерны
patterns = pyfpgrowth.find_frequent_patterns(transactions, 2)
#Выучим правила
rules = pyfpgrowth.generate_association_rules(patterns, 30);
#Покажем
rules

Реализация в R

В данном случае R не отстает от Питона: в такой удобной и родной arules библиотеке FP-Growth отсутствует.

В то же время, как и для Питона, реализация сущетсвует в Spark — [Ссылка]

А на самом деле...

А на самом деле, если вам захочется применять ARL в ваших бизнес задачах, мы настоятельно рекомендуем учить Java.

Weka (Waikato Environment for Knowledge Analysis). Это бесплатное ПО для Машинного Обучения, написанное на языке Java. Разаботано в Университете Waikato в Новой Зеландии в 1993. В Weka есть как GUI, так и возможность работы из командной строки. Из преимуществ можно назвать простоту в использовании графического интерфейса — нет необходимости писать код для решения прикладных задач. Для использования библиотек Weka в Python можно установить оболочку для Weka в Python: python-weka-wrapper3. Оболочка использует пакет javabridge для доступа к API Weka. Детальные инструкции по установке можно найти [здесь].

SPMF Это библиотека для интеллектуального анализа данных с открытым исходным кодом, написанная на Java, специализирующаяся на поиске паттернов в данных ([ссылка]). Заявляется, что в SPMF реализовано более 55 алгоритмов для майнинга данных. К сожалению, официальной оболочки SPMF для Python нет (по крайней мере на дату написания данной статьи)

Заключение или еще раз про эффективность

В заключении давайте эмпирически сравним эффективность метрикой runtime в зависимости от плотности датасета и длин транзакций датасета[9].

Под плотностью датасета подразумеваестя отношение транзакций, содержащих в себе частые items к общему количеству транзакций.

Эффективность алгоритмов при разной плотности датасетов

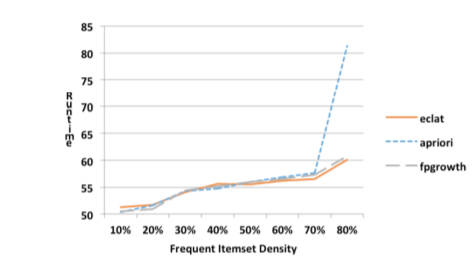
Из графика очевидно, что эффективность (чем меньше runtime, тем эффективнее) Apriori-алгоритма падает при увеличении плотности датасета.

Под длиной транзакции понимается количество в items в itemset

Эффективность алгоритмов при разной длине датасетов

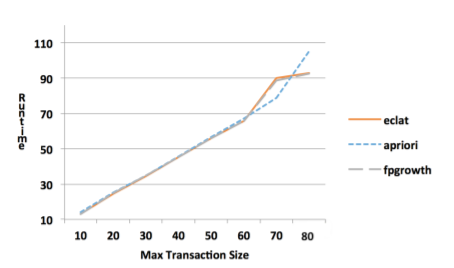
Очевидно, что при увеличении длины транзакции Apriori также справляется гораздо хуже.

К вопросу о подборе гиперпараметров

Самое время немного рассказать о том, как же подбирать гиперпараметры наших моделей (они же те самые support, confidence и т.д.)

Поскольку алгоритмы ARules чувствительны к гиперпараметрам, то необходимо грамотно подойти к вопросу о выборе. Разница во времени выполнения при различных комбинациях гиперпараметров может существенно отличаться.

Основным гиперпараметром в любом алгоритме ARules является min support. Он, грубо говоря, отвечает за минимальную относительную частоту ассоциативного правила в выборке. Выбирая данный показатель необходимо в первую очередь ориентироваться на поставленную задачу. Чаще всего заказчику необходимо небольшое количество топовых комбинаций, поэтому можно ставить высокое значение min support. Однако, в таком случае в нашу выборку могут попасть какие-то выбросы (bundle-товары, например) и не попасть какие-то интересные комбинации. В общем и целом, чем выше вы ставите значение суппорт, тем более мощные правила вы находите, и тем быстрее считается алгоритм. Мы рекомендуем при первом прогоне ставить значение поменьше, чтобы понять, какие пары, тройки и т.д. товаров вообще встречаются в датасете. Потом уже постепенно увеличивать шаг, добираясь до нужного значения (заданного заказчиком, например). На практике хорошим значением min supp будет и 0.1% (при очень большом датасете).

Ниже мы приводим примерный график зависимости времени выполнения алгоритма от данного показателя.

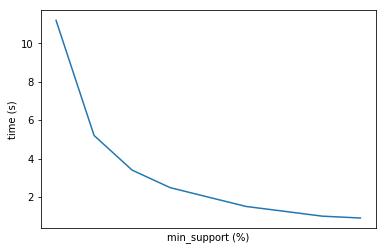
В общем, все как обычно зависит от задачи и данных.

Итоги

Итак, мы познакомились с базовой теорией ARL («кто купил х, также купил y») и основными понятиями и метриками (support, confidence, lift и conviction).

Посмотрели 3 самых популярных (и старых, как мир) алгоритма (Apriori, ECLAT, FP-Growth), позавидовали пользователям R и библиотеки arules, попробовали сами реализовать ECLAT.

Основные моменты:

1. ARL лежат в основе рекомендательных систем
2. ARL широко применимы — от традиционного ритейла и онлайн ритейла (от Ozon до Steam), обычных закупок ТМЦ до банков и телекома (подключаемые сервисы и услуги)
3. ARL относительно легко использовать, существуют реализации разного уровня проработки для разных задач.
4. ARL хорошо интепретируются и не требуют специальных навыков
5. При этом алгоритмы, особенно классические, нельзя назвать супер-эффективными. Если работать с ними из коробки на больших датасетах, может понадобиться большая вычислительная мощность. Но ничто не мешает нам их допиливать, правда?

Помимо рассмотренных бызовых алгоритмов существет модификации и ответвления:

Алгоритм CHARM для поиска замкнутых itemsets. Этот алгоритм отлично снижает сложность поиска правил с экспоненциальной (т.е. возрастающей при увеличении датасета, например) до полиномиальной. Под замкнутым itemset понимается такой itemset, для которого не существует суперсета (т.е. сета, включающего наш itemset + другие items) с такой же частотностью (=support).

Тут стоит немного пояснить — до сего момента мы рассматривали просто частые (frequent) itemsets. Существует также понятие замкнутых (см. выше) и максимальных. Максимальный itemset — это такой itemset, для которого не существует частого (=frequent) суперсета.

Отношения между этими тремя видами itemsets представлено на картинке ниже:

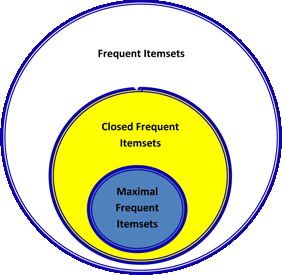
AprioriDP (Dynamic Programming) — позволяет хранить supp в специальной структуре данных, работает немного быстрее классического Apriori

FP Bonsai — улучшенный FP-Growth с обрезкой префиксного дерева (пример алгоритма с ограничениями)

В заключении не можем не упомянуть о сумрачном гении ARL докторе Кристиане Боргельте из Университета Констанца.

Кристиан реализовывал упомянутые нами алгоритмы на С, Python, Java и R. Ну или почти все. Существует даже GUI за его авторством, где в пару кликов можно загрузить датасет, выбрать нужный алгоритм и найти правила. Это при условии, что оно у вас заработает.

Для простых же задач достаточно и того, что мы рассмотрели в этой статье. А если недостаточно — призываем писать реализацию самим!

Использованная литература:

Discovery, analysis and presentation of strong rules. G. Piatetsky-Shapiro. Knowledge Discovery in Databases, AAAI Press, (1991)
Mining Association Rules between Sets of Items in Large Databases
Fast Algorithms for Mining Association Rules
Ask Dan!
Introduction to arules – A computational environment for mining association rules and frequent item sets
Публикации Д-ра Боргельта
J. Han, J. Pei, and Y. Yin, “Mining frequent patterns without candidate generation,” in ACM SIGMOD Record, vol. 29, no. 2. ACM, 2000, pp. 1–12.
Shimon, Sh. Improving Data mining algorithms using constraints. The Open University of Israel, 2012.
Jeff Heaton. Comparing Dataset Characteristics that Favor the Apriori, Eclat or FP-Growth Frequent Itemset Mining Algorithms
Исходники

Авторы: Павел Голубев, Николай Башлыков

Теги:

Хабы: