
Снова поговорим об ускорении работы клиентской стороны веб-приложения и о том, как для этого задействовать все вычислительные ресурсы процессора.
В предыдущей части мы нарисовали фрактал Ньютона с помощью WebAssembly на Rust. В этой части мы задействуем SIMD команды и параллельные вычисления, чтобы добиться ещё большей производительности.
Вживую увидеть прирост скорости можно на онлайн-демо. На моём компьютере она составляет ~900% по сравнению с обычной реализацией на wasm.
Тем, кто впервые слышит о WebAssembly на Rust или никогда с ними не сталкивался, рекомендую прочитать первую часть. Там подробно рассказано об основах работы с этими языками, а также о фрактале Ньютона.
Содержание:
Коротко о SIMD командах
SIMD — single instruction, multiple data. SIMD команды выполняют одновременно одно и то же действие сразу с несколькими наборами информации. Например, используя SIMD команду, можно сложить попарно друг с другом восемь чисел за то же время, за которое складываются два числа обычной командой.
Набором информации служит 64-, 128-, 256-, и уже даже 512-битный буфер, называемый вектором, и его данные хранятся в специальных векторных регистрах процессора. Для использования SIMD нужно сначала запаковать информацию в вектор требуемой величины. Для сложения восьми 32-битных чисел с плавающей точкой понадобится два 128-битных вектора: в каждом мы будем хранить по 4 числа, а затем одной командой складывать их:

В идеале прирост производительности от использования SIMD'ов равен отношению размера вектора к размеру одной переменной (в примере: 128 / 32 = 4). Однако, на практике прирост оказывается немного ниже, так как нам также нужно загружать в процессор во столько же раз больше информации. Программы, использующие один регистр, обычно называют скалярными, а те, что используют SIMD команды, векторными.
SIMD в Rust-WASM
В WebAssembly недавно была добавлена поддержка 128-битных SIMD команд. В Rust-wasm есть поддержка всех SIMD команд из wasm. Полный их список перечислен здесь.
Чтобы включить SIMD команды в Rust-wasm, нужно в самом начале файла lib.rs добавить глобальный атрибут
#![cfg(target_arch = "wasm32")]. Он подсказывает компилятору, что мы будем собирать проект под платформу wasm32, а значит, сможем использовать SIMD команды оттуда.#![cfg(target_arch = "wasm32")]
use geometry::{transform_point_to_plot_scale, PlotScale};
use memory_management::create_u32_buffer;
...▍ Простой пример
Знакомство с SIMD в wasm предлагаю начать с классической задачи по складыванию чисел из двух массивов в третий. Напишем две функции для выполнения этой задачи, одна из которых будем обрабатывать по одному элементу массива (скалярно), а другая — по четыре (векторно).
Со скалярной реализацией всё просто — создаём массив того же размера и проходим по каждому элементу, складывая значения из двух массивов в третий. Для простоты не будем проверять соответствие их размеров.
#[wasm_bindgen]
pub fn sum_numbers_scalar(arr1: Vec<f32>, arr2: Vec<f32>) -> Vec<f32> {
let length = arr1.len();
let mut result = vec![0f32; length];
for i in 0..length {
result[i] = arr1[i] + arr2[i];
}
return result;
}Для векторной реализации уже придётся прибегнуть к некоторым «хакам». Элементы в
Vec<T> хранятся в куче и располагаются друг за другом. Мы возьмём указатели на элементы массивов и будем интерпретировать каждые четыре элемента f32 как один SIMD-вектор v128. Затем используем функцию f32x4_add, которая складывает четыре f32 с другими четырьмя f32. Таким образом, нам потребуется в 4 раза меньше шагов, что одновременно и плюс, так как это быстрее, и минус, потому что если размер массива не будет кратен четырём, то последние элементы придётся заполнять скалярным способом. Но мы пока не будем акцентировать на этом внимание и представим, что кол-во элементов всегда кратно 4. Получится следующая функция (с подчёркивания начинаются имена векторных переменных):// Подключаем SIMD команды
use std::arch::wasm32::*;
// Специальный атрибут, позволяющий использовать SIMD команды
#[target_feature(enable = "simd128")]
#[wasm_bindgen]
pub fn sum_numbers_vector(arr1: Vec<f32>, arr2: Vec<f32>) -> Vec<f32> {
let length = arr1.len();
let mut result = vec![0f32; length];
// Берём указатели на элементы векторов (f32) и кастуем их к указателям на v128
let result_vec_ptr = result.as_mut_ptr() as *mut v128;
let arr1_vec_ptr = arr1.as_ptr() as *mut v128;
let arr2_vec_ptr = arr2.as_ptr() as *mut v128;
// Код помечем опасным, так как мы заполняем данные по указателю
unsafe {
// Шагов в четыре раза меньше
for i in 0..(length / 4) {
// Функция ptr.add(i) смещает указатель ptr на i * sizeof(T), где T — тип
// данных, на которые указывает указатель. В нашем случае это v128.
*result_vec_ptr.add(i) =
f32x4_add(
*arr1_vec_ptr.add(i),
*arr2_vec_ptr.add(i)
);
}
}
return result;
}Проверим для начала правильность работы наших SIMD инструкций.
JS скрипт для проверки
import {sum_numbers_scalar, sum_numbers_vector } from '../pkg/project_name.js';
const TEST_SUM_LENGTH = 10 * 4;
const TEST_SUM_COEF = 100;
// Создаём массив, заполненный случайными числами
function createRandomArray(length, coef) {
return Array.from(
{ length },
() => {
return (Math.random() - 0.5) * 2 * coef;
}
);
}
function testSum() {
let arr1 = createRandomArray(TEST_SUM_LENGTH, TEST_SUM_COEF);
let arr2 = createRandomArray(TEST_SUM_LENGTH, TEST_SUM_COEF);
let sumScalar = sum_numbers_scalar(arr1, arr2);
let sumVector = sum_numbers_vector(arr1, arr2);
console.log('sumScalar :>> ', sumScalar);
console.log('sumVector :>> ', sumVector);
}Если вы сделали всё правильно, то у вас должны получиться два одинаковых массива:

Теперь сравним скорость этих функций.
JS скрипт для проверки времени выполнения
import {sum_numbers_scalar, sum_numbers_vector } from '../pkg/project_name.js';
function testSum() {
let arr1 = createRandomArray(TEST_SUM_LENGTH, TEST_SUM_COEF);
let arr2 = createRandomArray(TEST_SUM_LENGTH, TEST_SUM_COEF);
let scalarStart = performance.now();
let sumScalar = sum_numbers_scalar(arr1, arr2);
let scalarEnd = performance.now();
let vectorStart = performance.now();
let sumVector = sum_numbers_vector(arr1, arr2);
let vectorEnd = performance.now();
let scalarElapsed = (scalarEnd - scalarStart).toFixed(2);
let vectorElapsed = (vectorEnd - vectorStart).toFixed(2);
console.log(`Elapsed: scalar: ${scalarElapsed}ms, vector: ${vectorElapsed}ms`);
}И при проверке мы увидим в консоли… что векторная реализация работает медленнее?

Так происходит из-за того, что компилятор оптимизирует скалярную реализацию до того же уровня скорости. Также стоит учесть, что наш вариант немного не оптимизирован: нам не нужно создавать новый массив для хранения сумм, мы можем сохранять их прямо в один из существующих массивов:
#[target_feature(enable = "simd128")]
#[wasm_bindgen]
pub fn sum_numbers_vector(mut arr1: Vec<f32>, arr2: Vec<f32>) -> Vec<f32> {
let length = arr1.len();
// let mut result = vec![0f32; length];
// let result_vec_addr = result.as_mut_ptr() as *mut v128;
let arr1_vec_addr = arr1.as_mut_ptr() as *mut v128;
let arr2_vec_addr = arr2.as_ptr() as *mut v128;
unsafe {
for i in 0..(length / 4) {
// Перезаписываем первый массив
*arr1_vec_addr.add(i) = f32x4_add(*arr1_vec_addr.add(i), *arr2_vec_addr.add(i));
}
}
return arr1;
}Теперь скорости обеих функций стали примерно равны:
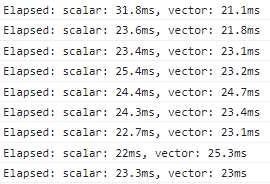
Но нам же интересен прирост производительности от применения SIMD! Чтобы его увидеть, установим уровень оптимизации в 0 в настройках проекта:
# Добавить в Cargo.toml
[profile.release]
opt-level = 0Теперь скалярная функция не будет оптимизирована. Соберём проект с этими настройками и снова посмотрим на скорость. У меня получились следующие результаты:
| Chrome scalar, ms | Chrome vector, ms | Chrome speed boost | Firefox scalar, ms | Firefox vector, ms | Firefox speed boost |
| 261 | 55 | 474% | 173 | 41 | 421% |
| 254 | 54 | 470% | 173 | 36 | 480% |
| 261 | 57 | 457% | 174 | 36 | 483% |
| 258 | 52 | 496% | 173 | 38 | 455% |
| 256 | 54 | 474% | 174 | 37 | 470% |
▍ Пример посложнее
Несмотря на повышенную скорость, у SIMD команд есть один существенный недостаток — с ними нельзя заблаговременно прервать вычисления при каком-то условии, касающегося одного элемента.
Представьте, что у вас есть
#[wasm_bindgen]
fn process_numbers(mut numbers: Vec<f32>, N: usize, K: usize, L: f32) -> Vec<usize> {
let mut iterations = vec![usize::MAX; N];
for i in 0..N { // Проход по каждому числу
for j in 0..K { // Обработка числа K раз
numbers[i] *= numbers[i];
if numbers[i] > L {
iterations[i] = j; // Запоминаем номер итерации для этого числа
break;
}
}
}
return iterations;
}Вот примерно такую же задачку мы решаем при рендеринге фрактала Ньютона. Только у нас комплексные числа и мы выполняем более сложные действия с ними.
А теперь попробуйте сделать то же самое с помощью SIMD команд. Так как они обрабатывают по несколько чисел за раз, то и прекратить цикл они могут только тогда, когда все числа будут соответствовать условию. Поэтому в данном случае SIMD команды будут непременно выполнять лишние вычисления с теми числами, которые уже удовлетворяют условию. Конечно, можно отдельно следить за каждым элементом в simd-векторе и заменять его на следующий по выполнению условия, но тогда придётся: а) следить за кол-вом итераций для каждого числа, б) по одному загружать числа в simd-вектор, в) совершать несколько проверок и битовых операций для проверки каждого элемента. В результате получается, что вместе с одновременным умножением четырёх чисел нам также потребуется проверять эти числа поодиночке.
Вместо этого, я предлагаю векторизировать абсолютно все вычисления:
#[wasm_bindgen]
#[target_feature(enable = "simd128")]
pub fn simd_process_numbers(mut numbers: Vec<f32>, N: usize, K: usize, L: f32) -> Vec<usize> {
let mut iterations = vec![usize::MAX; N];
let numbers_ptr = numbers.as_mut_ptr() as *mut v128; // [[n1, n2, n3, n4], ...]
let iterations_ptr = iterations.as_mut_ptr() as *mut v128; // [[i1, i2, i3, i4], ...]
let _L = f32x4_splat(L); // [L, L, L, L]
for i in 0..(N / 4) { // Проход по каждой четвёртке чисел
for j in 0..K { // Обработка четвёртки чисел K раз
unsafe {
let _iteration = u32x4_splat(j as u32); // [j, j, j, j]
let num_ptr = numbers_ptr.add(i); // [n1, n2, n3, n4]
let iter_ptr = iterations_ptr.add(i); // [i1, i2, i3, i4]
*num_ptr = f32x4_mul(*num_ptr, *num_ptr); // [n1 * n1, ..., n4 * n4]
let _gt_check = f32x4_gt(*num_ptr, _L); // [n1 > L, ..., n4 > L]
*iter_ptr = v128_bitselect( // Запоминаем номер итерации для чисел, превысивших порог
u32x4_min(_iteration, *iter_ptr), // новые значения: [min(i1, j), ..., min(i4, j)]
*iter_ptr, // старые значения
_gt_check,
);
if i32x4_all_true(_gt_check) { // Если все числа из [n1, n2, n3, n4] больше чем L,
break; // то прерываем цикл
}
}
}
}
return iterations;
}Как видим, даже такой, казалось бы, простой алгоритм в векторной реализации становится существенно запутаннее. Я попытался в комментариях в общих чертах объяснить, как он работает, но отдельно стоит сказать про функцию
v128_bitselect: она берёт биты из первого аргумента, если соответствующие биты третьего аргумента равны 1, иначе берутся значения битов второго аргумента. Иными словами, для каждого бита выполняется следующий метод:fn bitselect(bit1: bool, bit2: bool, bit3: bool) {
let bit: bool;
if bit3 {
bit = bit1;
} else {
bit = bit2;
}
}Давайте теперь проверим, правильно ли, вообще, работает эта функция.
JS скрипт для проверки
import {process_numbers, simd_process_numbers} from '../pkg/project_name.js';
const TEST_COEF = 2.5;
const N = 2 * 4;
const K = 6;
const L = 1000
function createRandomArray(length, coef) {
return Array.from(
{ length },
() => {
return (Math.random() - 0.5) * 2 * coef;
}
);
}
function testNumsProcessing() {
let arr = createRandomArray(N, TEST_COEF);
let scalar = Array.from(process_numbers(arr, N, K, L));
let vector = Array.from(simd_process_numbers(arr, N, K, L));
console.log('scalar :>> ', scalar);
console.log('vector :>> ', vector);
}Результаты:
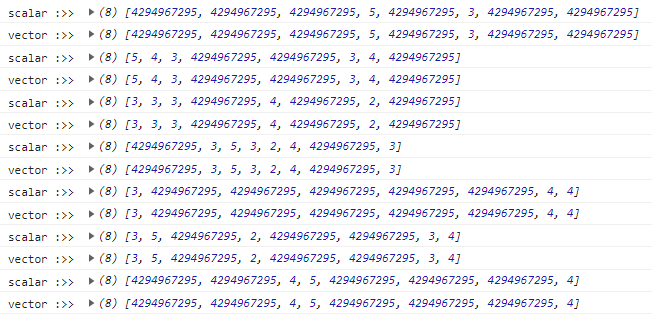
По крайней мере, работает правильно. Что насчёт скорости?
JS скрипт для проверки времени выполнения
import {process_numbers, simd_process_numbers} from '../pkg/project_name.js';
const TEST_COEF = 2.5;
const N = 100_000 * 4;
const K = 6;
const L = 10000
function createRandomArray(length, coef) {
return Array.from(
{ length },
() => {
return (Math.random() - 0.5) * 2 * coef;
}
);
}
function testNumsProcessing() {
let arr = createRandomArray(N, TEST_COEF);
let scalarStart = performance.now();
let scalar = Array.from(process_numbers(arr, N, K, L));
let scalarEnd = performance.now();
let vectorStart = performance.now();
let vector = Array.from(simd_process_numbers(arr, N, K, L));
let vectorEnd = performance.now();
let scalarElapsed = (scalarEnd - scalarStart).toFixed(2);
let vectorElapsed = (vectorEnd - vectorStart).toFixed(2);
console.log(`Elapsed: scalar: ${scalarElapsed}ms, vector: ${vectorElapsed}ms`);
}Без оптимизации (opt-level = 0), те же исходные данные, только чисел 400000, а не 8:

В среднем ускорение составляет 540%. Однако если скомпилировать код с максимальным уровнем оптимизации
opt-level = 3, то прироста практически нет.
Результаты сравнения скорости при максимальной оптимизации


На этом этапе у вас резонно может возникнуть вопрос «А зачем самим использовать SIMD инструкции, если компилятор может сам догадаться, как их применить?». На практике компилятор не всегда эффективно выполняет векторизацию вычислений, если он вообще сумеет до неё додуматься. Поэтому в действительно сложных вычислениях приходится самим векторизировать вычисления.
Небольшой математический бонус
Эту задачку можно решить и без циклов. Внимательные читатели могут заметить, что умножение числа  самого на себя
самого на себя  раз можно представить в виде следующей функции:
раз можно представить в виде следующей функции:
Тогда можно сразу узнать на каком число
число  превысит пороговое значение
превысит пороговое значение  :
:
Учитывая, что — целое число, оно находится так:
— целое число, оно находится так:
Тогда можно сразу узнать на каком
Учитывая, что
▍ Используем SIMD команды для фрактала Ньютона
Сейчас функция для отображения фрактала Ньютона выглядит следующим образом:
#[wasm_bindgen]
pub fn generate_fractal_image(
roots: JsValue,
roots_colors: JsValue,
plot_scale: &PlotScale,
iterations_count: usize,
) -> *mut [u8; 4] {
let roots: Vec<Complex32> = roots
.into_serde::<Vec<MyComplex32>>()
.unwrap()
.into_iter()
.map(|z| z.into())
.collect();
let roots_colors: Vec<[u8; 4]> = roots_colors.into_serde().unwrap();
let &PlotScale { width, height, .. } = plot_scale;
let (width, height) = (width as usize, height as usize);
let length = width * height;
let image_data = create_u32_buffer(length) as *mut [u8; 4];
for i in 0..length {
let x = i % width;
let y = i / width;
let (re, im) = transform_point_to_plot_scale(x as f32, y as f32, &plot_scale);
let z = Complex32 { re, im };
let root_id = get_root_id(z, &roots, iterations_count);
unsafe {
*image_data.add(i) = roots_colors[root_id];
}
}
return image_data;
}Поиск ближайшего корня:
pub fn get_root_id(mut z: Complex32, roots: &[Complex32], iterations_count: usize) -> usize {
for _ in 0..iterations_count {
let mut sum = Complex32::new(0.0, 0.0);
for (i, root) in roots.iter().enumerate() {
let mut diff = z - root;
let square_norm = diff.norm_sqr();
if square_norm < MIN_DIFF {
return i;
}
diff.re /= square_norm;
diff.im /= -square_norm;
sum += diff;
}
z -= 1.0 / sum;
}
let mut min_distance = f32::MAX;
let mut closest_root_id: usize = 0;
for (i, root) in roots.iter().enumerate() {
let distance = (z - root).norm_sqr();
if distance < min_distance {
min_distance = distance;
closest_root_id = i;
}
}
closest_root_id
}О том, как получилось эти функции, рассказано в первой части.
После векторизации они стали в несколько раз сложнее, а ещё появилось несколько новых функций для выполнения SIMD-арифметики. Я не буду подробно расписывать, как работает этот код,
SIMD: отображение фрактала
Исходный код.
#[target_feature(enable = "simd128")]
pub fn fill_pixels_simd(
roots: Vec<Complex32>,
roots_colors: Vec<u32>,
plot_scale: &PlotScale,
iterations_count: usize,
image_data: *mut (u32, u32, u32, u32), // Заполняем сразу по 4 пикселя
) {
let PlotScale {
x_display_range: width,
y_display_range: height,
..
} = *plot_scale;
let (w_int, h_int) = (width as usize, height as usize);
let length = w_int * h_int;
// [width, width, width, width]
let _width = f32x4_splat(width);
unsafe {
let simd_length = length / 4;
for i in 0..simd_length {
// [4i, 4i, 4i, 4i] (тут i - это не мнимая единица)
let mut _i = f32x4_splat((4 * i) as f32);
// [4i + 0, 4i + 1, 4i + 2, 4i + 3]
_i = f32x4_add(_i, f32x4(0.0, 1.0, 2.0, 3.0));
// [(4i + 0) % width, ..., (4i + 3) % width ]
let _xs = SimdMath::f32x4_mod(_i, _width); // Подробно об этой и других SIMD функциях - ниже
// [⌊(4i + 0) / width⌋, ..., ⌊(4i + 3) / width⌋]
let _ys = f32x4_floor(f32x4_div(_i, _width));
// Находим номера корней для каждого из четырёх пикселей
let (id0, id1, id2, id3) =
simd_get_root_id(_xs, _ys, roots.as_ref(), iterations_count, &plot_scale);
// Заполняем цвета пикселей
*(image_data.add(i)) = transmute([
roots_colors[id0 as usize],
roots_colors[id1 as usize],
roots_colors[id2 as usize],
roots_colors[id3 as usize],
]);
}
// Заполняем пиксели, непоместившиеся в пачки по четыре
// Алгоритм точно такой же, как и в скалярной реализации
let image_data_as_u32 = image_data as *mut u32;
for i in (simd_length * 4)..length {
let (x, y) =
transform_point_to_plot_scale((i % w_int) as f32, (i / w_int) as f32, &plot_scale);
*image_data_as_u32.add(i) =
roots_colors[get_root_id(Complex32::new(x, y), roots.as_ref(), iterations_count)];
}
}
}
SIMD: поиск ближайшего корня
Исходный код.
// Обрабатываем сразу 4 точки за раз
#[target_feature(enable = "simd128")]
pub unsafe fn simd_get_root_id(
_xs: v128,
_ys: v128,
roots: &[Complex32],
iterations_count: usize,
plot_scale: &PlotScale,
) -> (u32, u32, u32, u32) {
let mut _min_distances = SimdMath::_F32_MAX;
let mut _closest_root_ids = SimdMath::_I32_ZERO;
// Первые две точки
let mut _points1 = f32x4(
f32x4_extract_lane::<0>(_xs),
f32x4_extract_lane::<0>(_ys),
f32x4_extract_lane::<1>(_xs),
f32x4_extract_lane::<1>(_ys),
);
// Вторые две точки
let mut _points2 = f32x4(
f32x4_extract_lane::<2>(_xs),
f32x4_extract_lane::<2>(_ys),
f32x4_extract_lane::<3>(_xs),
f32x4_extract_lane::<3>(_ys),
);
// Конвертируем положение точек из координат изображения
// в координаты отображаемого пространства
_points1 = simd_transform_point_to_plot_scale(_points1, &plot_scale);
_points2 = simd_transform_point_to_plot_scale(_points2, &plot_scale);
for _ in 0..iterations_count {
// Выполняем метод Ньютона для каждой пары точек.
// Заметьте, что здесь нет преждевременного выхода из цикла!
_points1 = simd_newton_method_approx_for_two_numbers(_points1, &roots);
_points2 = simd_newton_method_approx_for_two_numbers(_points2, &roots);
}
// Находим ближайшие корни для каждой из четырёх точек
for (i, &root) in roots.iter().enumerate() {
// [i, i, i, i]
let _ids = i32x4_splat(i as i32);
// [rx, ry, rx, ry] - координаты корней
let _roots = v128_load64_splat(addr_of!(root) as *const u64);
// [dist(p1, r), dist(p1, r), dist(p2, r), dist(p2, r)] - расстояния от первой пары точек до корня
let _dists1 = SimdMath::calculate_squared_distances(_points1, _roots);
// [dist(p3, r), dist(p3, r), dist(p4, r), dist(p4, r)] - расстояния от второй пары точек до корня
let _dists2 = SimdMath::calculate_squared_distances(_points2, _roots);
// [dist(p1, r), dist(p2, r), dist(p3, r), dist(p4, r)] - расстояния от каждой точки до корня
let _distances = i32x4_shuffle::<0, 2, 4, 6>(_dists1, _dists2);
// Проверка меньше ли новое расстояние от этой точки, чем предыдущее
let _le_check = f32x4_lt(_distances, _min_distances);
// Установка нового минимального расстояния для каждой точки
_min_distances = v128_bitselect(_distances, _min_distances, _le_check);
// Установка нового номера ближайшего корня для каждой точки
_closest_root_ids = v128_bitselect(_ids, _closest_root_ids, _le_check);
}
// Интерпретируем v128 как четыре u32
return transmute::<v128, (u32, u32, u32, u32)>(_closest_root_ids);
}
SIMD: метод Ньютона
Исходный код.
// Выполняем метод Ньютона сразу для двух комплексных чисел,
// чтобы при поиске ближайшего корня задействовать все четыре
// векторных регистра
#[inline]
#[target_feature(enable = "simd128")]
pub unsafe fn simd_newton_method_approx_for_two_numbers(two_z: v128, roots: &[Complex32]) -> v128 {
let ptr = addr_of!(two_z) as *const u64;
u64x2(
simd_newton_method_approx(*ptr, roots),
simd_newton_method_approx(*(ptr.offset(1)), roots),
)
}
#[inline]
#[target_feature(enable = "simd128")]
pub fn simd_newton_method_approx(z: u64, roots: &[Complex32]) -> u64 {
// [re1: 0, im1: 0, re2: 0, im2: 0]
let mut _sums = SimdMath::_F32_ZERO;
// [re, im, re, im]
let _z = unsafe { v128_load64_splat(&z) };
// Обрабатываем по 2 корня за раз
// [r1.re, r1.im, r2.re, r2.im]: r1, r2 - корни
let roots_chunks_iter = roots.chunks_exact(2);
let rem = roots_chunks_iter.remainder();
for roots_chunk in roots_chunks_iter {
unsafe {
// Формула в общем виде: sum += 1.0 / (z - root)
// 1. Вычитание: z - root
let _diffs = f32x4_sub(_z, *(roots_chunk.as_ptr() as *const v128));
let _square_norms = SimdMath::calculate_square_norms(_diffs);
// 1*. Проверка: if (difference < 0.001) => z - один из корней
if v128_any_true(f32x4_lt(_square_norms, _MIN_DIFFS)) {
return z;
}
// 2. Инверсия: 1.0 / (z - root)
let mut _inversions = f32x4_mul(_diffs, SimdMath::_NEGATION_MASK_FOR_INVERSION);
_inversions = f32x4_div(_inversions, _square_norms);
// 3. Сложение: sum += 1.0 / (z - root)
_sums = f32x4_add(_sums, _inversions);
}
}
// [re2, im2, re1, im1]
let _sums_shifted = i8x16_swizzle(
_sums,
i8x16(8, 9, 10, 11, 12, 13, 14, 15, 0, 1, 2, 3, 4, 5, 6, 7),
);
// Обработка нечётного корня, если такой есть
if let Some(rem) = rem.get(0) {
unsafe {
// Эта часть кода делаётся всё то же самое, что и предыдущий цикл,
// за исключением того, что второе комплексное значение в векторе
// равно 0: [r1.re, r1.im, 0, 0]
let _diffs = f32x4_sub(_z, v128_load64_zero(addr_of!(*rem) as *const u64));
let _square_norms = SimdMath::calculate_square_norms(_diffs);
if (i8x16_extract_lane::<0>(f32x4_lt(_square_norms, _MIN_DIFFS)) & 1) == 1 {
return z;
}
let mut _inversions = f32x4_mul(_diffs, SimdMath::_NEGATION_MASK_FOR_INVERSION);
_inversions = f32x4_div(_inversions, _square_norms);
_sums = f32x4_add(_sums, _inversions);
}
}
// [re1 + re2, im1 + im2, re1 + re2, im1 + im2]
_sums = f32x4_add(_sums, _sums_shifted);
// z - 1.0 / sum
unsafe {
// 1.0 / sum
let _inversions = SimdMath::complex_numbers_inversion(_sums);
// z - (1.0 / sum)
let _subs = f32x4_sub(_z, _inversions);
*(addr_of!(_subs) as *const u64)
}
}
SIMD: математика
pub struct SimdMath;
impl SimdMath {
pub const _F32_ZERO: v128 = f32x4(0.0, 0.0, 0.0, 0.0);
pub const _F32_MAX: v128 = f32x4(f32::MAX, f32::MAX, f32::MAX, f32::MAX);
pub const _I32_ZERO: v128 = i32x4(0, 0, 0, 0);
pub const _NEGATION_MASK_FOR_INVERSION: v128 = f32x4(1.0, -1.0, 1.0, -1.0);
// a % b = a - b * floor(a / b)
#[target_feature(enable = "simd128")]
pub fn f32x4_mod(_a: v128, _b: v128) -> v128 {
f32x4_sub(_a, f32x4_mul(_b, f32x4_floor(f32x4_div(_a, _b))))
}
// Квадратная норма z (a: re, b: im) = a^2 + b^2
#[target_feature(enable = "simd128")]
pub fn calculate_square_norms(_vec: v128) -> v128 {
// [a^2, b^2, a^2, b^2]
let _squares = f32x4_mul(_vec, _vec);
// [b^2, a^2, b^2, a^2]
let _shifted_squares = i8x16_swizzle(
_squares,
i8x16(4, 5, 6, 7, 0, 1, 2, 3, 12, 13, 14, 15, 8, 9, 10, 11),
);
// [
// a^2 + b^2,
// a^2 + b^2,
// a^2 + b^2,
// a^2 + b^2
// ]
f32x4_add(_squares, _shifted_squares)
}
// Формула:
// 1 / z
// = 1 / (a + bi)
// = a / (a^2 + b^2) - bi / (a^2 + b^2)
// Real: a / (a^2 + b^2)
// Imagine: -b / (a^2 + b^2)
#[target_feature(enable = "simd128")]
pub fn complex_numbers_inversion(_vec: v128) -> v128 {
// [a, -b, a, -b]
let _numerators = f32x4_mul(_vec, SimdMath::_NEGATION_MASK_FOR_INVERSION);
// [
// a^2 + b^2,
// a^2 + b^2,
// a^2 + b^2,
// a^2 + b^2
// ]
let _denumerators = SimdMath::calculate_square_norms(_numerators);
// [
// a / (a^2 + b^2),
// -b / (a^2 + b^2),
// a / (a^2 + b^2),
// -b / (a^2 + b^2)
// ]
f32x4_div(_numerators, _denumerators)
}
// Формула:
// Расстояние = sqrt((x1 - x2)^2 + (y1 - y2)^2)
// _points1: (x1, y1, x3, y3)
// _points2: (x2, y2, x4, y4)
#[target_feature(enable = "simd128")]
pub fn calculate_squared_distances(_points1: v128, _points2: v128) -> v128 {
// [
// x1 - x2 (= A),
// y1 - y2 (= B),
// x3 - x4 (= C),
// y3 - y4 (= D)
// ]
let _diffs = f32x4_sub(_points1, _points2);
// [
// A^2 + B^2,
// A^2 + B^2,
// C^2 + D^2,
// C^2 + D^2
// ]
SimdMath::calculate_square_norms(_diffs)
}
}Как правило, во сколько раз больше операций могут выполнять SIMD команды за раз, во столько же раз страшнее выглядит код с ними. Тем не менее на моём компьютере он обеспечивает прирост производительности в ~2.2 раза. Проверить всё так же можно на онлайн-демо. Для этого в выпадающем списке переключайте опции «CPU-wasm-scalar» и «CPU-wasm-simd».
Любопытно: если в скалярной и векторной реализации устанавливать один и тот же цвет для точек, которые оказались достаточно близко к корням после применения метода Ньютона…
if square_norm < MIN_DIFF {
return 3; // Возвращаем номер четвёртого цвета
}
...
if v128_any_true(f32x4_lt(_square_norms, _MIN_DIFFS)) {
return 3; // Возвращаем номер четвёртого цвета
}… то мы получим интересную картинку:
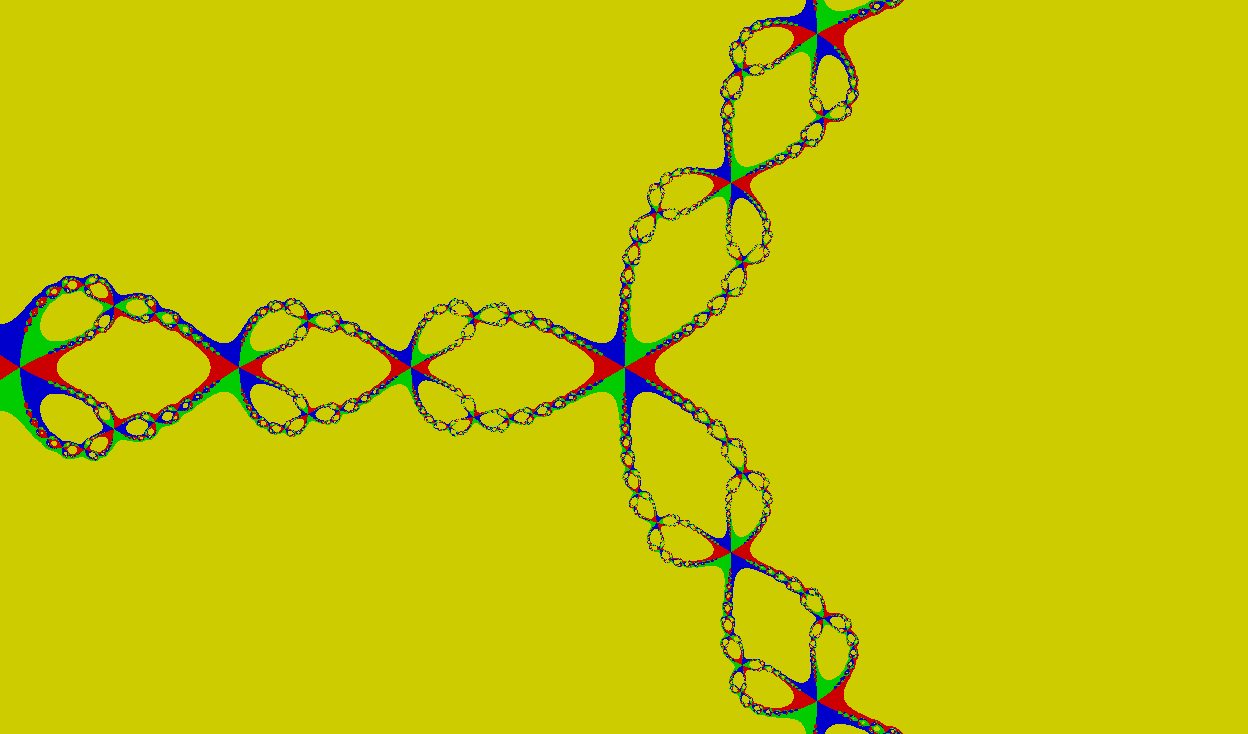
Все жёлтые пиксели, которые вы видите, оказались достаточно близко к корням после очередной итерации и удовлетворили условию преждевременного выхода из цикла. Для них не запускался цикл для поиска ближайшего корня, который занимает 15% всего времени исполнения алгоритма.
Теперь давайте вообще уберём эту проверку, которая сильно замедляет SIMD-алгоритм, и посмотрим на скорость скалярной и векторной реализаций:
Картинка практически не изменилась
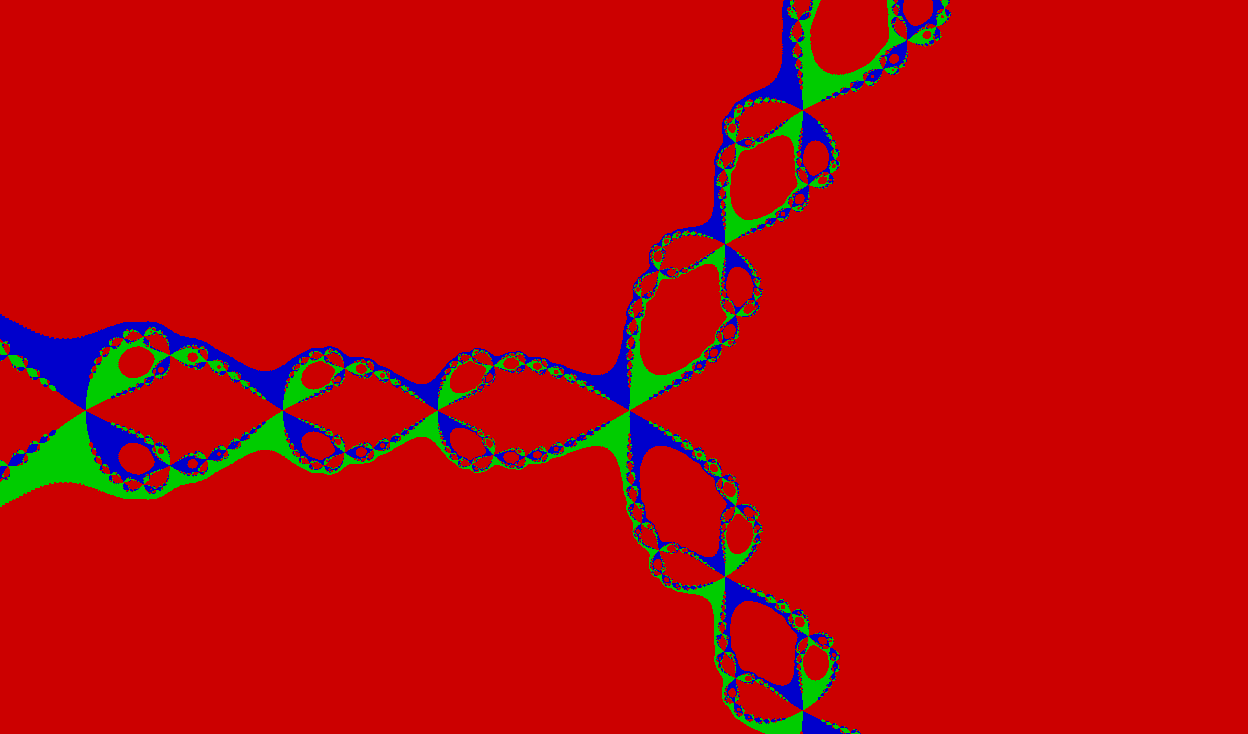

На моём компьютере я получил в среднем 4.9 FPS у скалярной и 18.4 FPS у векторной функции, то есть ускорение составляет ~375%, что практически соответствует максимально возможным 400% (так как мы обрабатываем за раз 128 бит вместо 32). Это означает, что SIMD реализация практически максимально оптимизирована в плане линейных вычислений.
Я пытался ещё несколько раз переписать этот алгоритм, используя другие подходы, но мне никак не удавалось достичь того же уровня производительности. Поэтому я остановился на этом варианте. Пускай код и выглядит довольно громоздким, но, зато с точки зрения векторизации, он практически максимально оптимальный.
Мультипоточность в браузерах
На сегодняшний день единственный способ выполнять код в браузере на нескольких ядрах процессора — это использовать WebWorker'ы. Веб-воркеры создаются на основе JS файла, который они будут исполнять в фоновом потоке, следующим образом:
new Worker("worker.js"). Этот поток обладает изолированным глобальным контекстом. Обмен информацией между воркерами и родительским потоком происходит с помощью функции postMessage, которая отправляет данные в обе стороны и подписки на колбэк onmessage с обеих сторон, вызывающегося при каждом вызове postMessage.В целом для распределённых вычислений в браузере совершенно не нужен WebAssembly (и в онлайн-примере есть даже возможность запустить JS код на всех ядрах), но если вам потребовалась мультипоточность, то, скорее всего, вы боретесь за производительность, а wasm — основа надёжной производительности. Поэтому дальше я буду рассказывать уже о нюансах, возникающих при использовании веб-воркеров с Rust-wasm. И хотя уже существуют готовые библиотеки для автоматического распределения вычислений на несколько потоков (например, rayon в wasm), мы будем вручную организовывать процесс параллельного выполнения кода, чтобы лучше понять стоящие за ним технологии.
▍ Rust-wasm в веб-воркерах
JS скрипты, выполняемые в потоке веб-воркеров, работают почти также, как и в главном потоке. Единственное отличие заключается в подключении других JS скриптов. Оно выполняется с помощью функции
importScripts. Также JS скрипты можно импортировать в виде ECMAScript модулей (через import), но для этого требуются модульные веб-воркеры. Они, на мой взгляд, намного удобнее, поэтому мы будем использовать именно их. Однако стоит учитывать, что модульные веб-воркеры по-прежнему не поддерживаются в Firefox. Эту проблему можно решить, добавив на нашу html страничку следующий «полифил». Этот код вручную добавляет поддержку для модульных веб-воркеров.Теперь попробуем использовать wasm модуль в воркера. Создадим простой воркер, который будет выводить назначаемый нами id и складывать два числа с помощью wasm:
// Файл worker.js
import init, { sum } from '../pkg/project_name.js';
async function run() {
// Загрузка wasm модуля
await init("../pkg/project_name_bg.wasm");
}
run();
// Устанавливаем колбэк на принимаемые воркером сообщения
onmessage = function (message) {
let data = message.data;
let id = data.id;
let nums = data.nums;
let [a, b] = [nums[0], nums[1]];
// Использование wasm модуля
let result = sum(a, b);
console.log(`Worker #${id}: ${a} + ${b} = ${result}`);
}Теперь создадим сразу несколько веб-воркеров с этим кодом в главном JS скрипте:
const WORKERS_COUNT = 4;
for (let i = 0; i < WORKERS_COUNT; i++) {
let worker = new Worker('worker.js', { type: 'module' });
// Отправляем сообщение воркерам с задержкой в секунду,
// чтобы wasm модуль успел загрузиться
setTimeout(() => {
// Отправка сообщения воркеру
// Просим его сложить i + i*i
worker.postMessage({ id: i, nums: [i, i * i] });
}, 1000);
}При запуске мы увидим четыре сообщения в хаотичном порядке:

Теперь у каждого воркера есть свой wasm модуль со своей отдельной памятью. Мы можем генерировать какие-то данные (например, цвета пикселей изображения) в каждом из воркеров, потом возвращать их оттуда в главный поток, где они будут объединяться в один массив/строку/изображение. Однако оптимальнее было бы, если бы все воркеры обладали единой wasm памятью и генерируемые ими данные располагались в памяти линейно, то есть друг за другом.
К счастью, и wasm модули, и веб-воркеры поддерживают разделяемый буфер
SharedArrayBuffer. Это такой же ArrayBuffer, только к нему имеют доступ все ядра процессора и поэтому его можно передавать между веб-воркерами через postMessage, позволяя им работать с одной и той же памятью. Таким образом, мы сможем производить вычисления сразу на нескольких ядрах и записывать результаты в одном месте.Для достижения этого нужно выполнить несколько шагов:
- Получить разрешение от браузера на использование
SharedArrayBuffer. - Позволить wasm модулю использовать разделяемую память.
▍ Разрешение на использование SharedArrayBuffer в браузере
Если вы прямо сейчас откроете консоль разработчика и попробуете создать объект
SharedArrayBuffer, то у вас ничего не выйдет:
Это происходит из-за того, что объект
SharedArrayBuffer можно использовать только в безопасном контексте. Чтобы получить к нему доступ, нужно чтобы ваш сервер отправлял следующие хидеры:Cross-Origin-Opener-Policy: same-origin
Cross-Origin-Embedder-Policy: require-corpПодробнее изучить требования можно тут.
Если у вас нет возможности контролировать отправляемые сервером хидеры (например, при хостинге сайта через простой локальный сервер или гитхаб), то можно воспользоваться небольшим лайфхаком.
Как изменить хидеры, если нет управления над сервером
Нужно создать сервисный воркер и с помощью него перехватывать отправляемые сервером пакеты и добавлять в них нужные хидеры. Для этого создадим скрипт serviceWorker.js, который будет исполняться сервис воркером:
И добавим на нашу html страничку следующий скрипт:
Всё! Теперь, если вы перезагрузите свой сайт (на всякий случай лучше очистить куки и кэш), то сможете пользоваться объектом
P. S. Идея — не моя, я её подсмотрел тут.
self.addEventListener("install", function () {
self.skipWaiting();
});
self.addEventListener("activate", (event) => {
event.waitUntil(self.clients.claim());
});
self.addEventListener("fetch", function (event) {
if (event.request.cache === "only-if-cached" && event.request.mode !== "same-origin") {
return;
}
event.respondWith(
fetch(event.request)
.then(function (response) {
if (response.status == 0) {
return response;
}
// Добавляем нужные хидеры
const newHeaders = new Headers(response.headers);
newHeaders.set("Cross-Origin-Embedder-Policy", "require-corp");
newHeaders.set("Cross-Origin-Opener-Policy", "same-origin");
const moddedResponse = new Response(response.body, {
status: response.status,
statusText: response.statusText,
headers: newHeaders,
});
return moddedResponse;
})
.catch(function (e) {
console.error(e);
})
);
});И добавим на нашу html страничку следующий скрипт:
<script type="module">
if ("serviceWorker" in navigator) {
// Регистрация сервисного воркера
navigator.serviceWorker.register(new URL("./serviceWorker.js", import.meta.url)).then(
function (registration) {
console.log("COOP/COEP Service Worker registered", registration.scope);
if (!navigator.serviceWorker.controller) {
window.location.reload();
}
},
function (err) {
console.log("COOP/COEP Service Worker failed to register", err);
}
);
} else {
console.warn("Cannot register a service worker");
}
</script>
Всё! Теперь, если вы перезагрузите свой сайт (на всякий случай лучше очистить куки и кэш), то сможете пользоваться объектом
SharedArrayBuffer.P. S. Идея — не моя, я её подсмотрел тут.
▍ Использование разделяемой памяти wasm модулем
Чтобы сборка нашего wasm модуля могла базироваться на разделяемой памяти, нужно выполнить ряд настроек. Вначале нам нужно будет переключиться на «nightly» версию компилятора. «Ночная» версия компилятора отличается поддержкой экспериментальных возможностей языка. Сделать это можно несколькими способами, я расскажу про, по моему мнению, самый простой и удобный. Он позволяет устанавливать тип версии индивидуально для каждого проекта. Для этого нужно открыть корневую папку проекта и ввести в консоль следующую команду:
rusutp override set nightly
После должно вывестись сообщение, что тулчейн переключился на «ночную» сборку языка.
Теперь нам нужно включить некоторые экспериментальные возможности языка, необходимые для использования атомарных операций и разделяемой памяти в wasm. Для этого нужно в корне проекта создать папку
.cargo, а в ней — файл конфигурации config.toml со следующим содержимым:[target.wasm32-unknown-unknown]
rustflags = ["-C", "target-feature=+atomics,+bulk-memory,+mutable-globals"]
[unstable]
build-std = ["panic_abort", "std"]
После сборки проекта с этими настройками в сгенерированной JS функции инициализации wasm модуля
init появится новый аргумент типа WebAssembly.Memory. Теперь мы можем передавать в wasm модуль вручную созданный объект разделяемой памяти wasm.Создадим эту память в главном потоке и передадим её воркерам через postMessage:
// Создаём разделяемую память с изначальным размером в
// 100 страниц (6.4MB) и максимальным — 1000 страниц (64MB)
let sharedMemory = new WebAssembly.Memory({ initial: 100, maximum: 1000, shared: true });
const WORKERS_COUNT = 4;
for (let i = 0; i < WORKERS_COUNT; i++) {
let worker = new Worker('worker.js', { type: 'module' });
// Делимся разделяемой памятью с веб-воркером
worker.postMessage(sharedMemory);
setTimeout(() => {
worker.postMessage({ id: i, nums: [i, i * i] });
}, 1000);
}Примем память в воркерах и воспользуемся ею для инициализации wasm модулей:
import init, { sum } from '../pkg/project_name.js';
// Колбэк-затычка для принятия wasm памяти. Срабатывает один раз.
onmessage = async function(message) {
// Разделяемая память
let sharedMemory = message.data;
// Инициализация wasm модуля с разделяемой памятью
await init("../pkg/project_name_bg.wasm", sharedMemory);
// Меняем колбэк-затычку на настоящий колбэк
onmessage = actualCallback;
}
// Настоящий колбэк
function actualCallback(message) {
let data = message.data;
let id = data.id;
let nums = data.nums;
let [a, b] = [nums[0], nums[1]];
// Использование wasm модуля
let result = sum(a, b);
console.log(`Worker #${id}: ${a} + ${b} = ${result}`);
}Пока что в работе нашего приложения ничего не поменялось. Давайте попробуем заполнить какой-нибудь буфер, используя воркеров. Разделим буфер на четыре куска и прикажем каждому из наших воркеров заполнить отдельный кусок.
Возьмём буфер u32 чисел и заполним значение каждого элемента номером этого элемента:
// buff_ptr - указатель на буфер
// buff_length - кол-во элементов u32 в нём
// buff_parts - на сколько частей разделяем буфер (т. е. сколько потоков будет его заполнять)
// part_num - номер части, которую нужно заполнить
#[wasm_bindgen]
pub fn fill_buffer(buff_ptr: *mut u32, buff_length: usize, buff_parts: usize, part_num: usize) {
let offset = buff_length / buff_parts;
let begin = part_num * offset;
let end = (part_num + 1) * offset;
for i in begin..end {
unsafe {
// Заполняем буфер
*buff_ptr.add(i) = i as u32;
}
}
}Чтобы веб-воркеры знали, какую часть буфера заполнять, мы должны создать его в главном потоке и оттуда же говорить воркерам заполнить определённый сегмент. Затем нужно дождаться, пока все воркеры не выполнят заполнение:
// Главный поток
import init, { create_u32_buffer, free_u32_buffer } from '../pkg/project_name.js';
const BUFF_LENGTH = 16;
const WORKERS_COUNT = 4;
async function run() {
let sharedMemory = new WebAssembly.Memory({ initial: 100, maximum: 1000, shared: true });
await init("../pkg/project_name_bg.wasm", sharedMemory);
let buffPtr = create_u32_buffer(BUFF_LENGTH);
// Кол-во воркеров, закончивших заполнение буфера
let doneWorkersCount = 0;
function workerCallback() {
doneWorkersCount += 1;
// Выводим массив по окончании заполнения
if (doneWorkersCount == WORKERS_COUNT) {
let u32Array = new Uint32Array(sharedMemory.buffer, buffPtr, BUFF_LENGTH);
console.log('u32Array :>> ', u32Array);
// ...и не забываем чистить память
free_u32_buffer(buffPtr, BUFF_LENGTH);
}
}
for (let i = 0; i < WORKERS_COUNT; i++) {
let worker = new Worker('worker.js', { type: 'module' });
// Увеличиваем кол-во закончивших работу воркеров на 1
// при поступлении сообщения от одного из них
worker.onmessage = workerCallback;
worker.postMessage(sharedMemory);
// Отправляем данные о буфере
setTimeout(() => {
worker.postMessage({
buffPtr,
buffLength: BUFF_LENGTH,
buffParts: WORKERS_COUNT,
partNum: i
});
}, 1000);
}
}
run();В воркере нам нужно принять эти данные и ответить главному потоку, когда мы закончим работу:
// Веб-воркер
import init, { fill_buffer } from '../pkg/project_name.js';
onmessage = async function (message) {
let sharedMemory = message.data;
await init("../pkg/project_name_bg.wasm", sharedMemory);
onmessage = actualCallback;
}
function actualCallback(message) {
let data = message.data;
let { buffPtr, buffLength, buffParts, partNum } = data;
// Заполняем буфер по переданным данным
fill_buffer(buffPtr, buffLength, buffParts, partNum);
postMessage("done"); // Можно отправить что угодно
}При запуске сайта мы обнаружим в консоли правильно заполненный массив:

Давайте теперь увеличим размер буфера до 1 млн и усложним вычисления поиском чисел Фибоначчи, чтобы пронаблюдать в диспетчере задач возросшую нагрузку на ядра процессора:
...
// Главный поток
const BUFF_LENGTH = 1_000_000;
...fn fibonacci(n: u32) -> u32 {
let (mut a, mut b) = (0, 1);
for _ in 0..n {
(a, b) = (b, a + b);
}
return a;
}
#[wasm_bindgen]
pub fn fill_buffer(buff_ptr: *mut u32, buff_length: usize, buff_parts: usize, part_num: usize) {
let offset = buff_length / buff_parts;
let begin = part_num * offset;
let end = (part_num + 1) * offset;
for i in begin..end {
unsafe {
// Заполняем буфер числами Фибоначчи
*buff_ptr.add(i) = fibonacci(i as u32);
}
}
}На моём компьютере буфер заполнялся ~1-2 минуты. В профайлере CPU получился очень характерный график нагрузки:

Видно, что вначале процессор был загружен почти на 100%. Дальше видны несколько спадов нагрузки — это моменты, когда каждый из воркеров завершал заполнение своего сегмента. Чем больше числа, тем дольше работает функция для поиска чисел Фибоначчи, и поэтому воркеры завершали работу не одновременно, а по порядку.
Замечательно ещё и то, что, хотя я использовал всего 4 воркера, мой 8-ядерный процессор всё равно был нагружен на ~90%. Это происходит из-за того, что потоки веб-воркеров не являются потоками на уровне железа. Ими управляет браузер, который, в свою очередь, порождает потоки на уровне ОС.
Для сравнения вот так выглядит нагрузка на процессор с одним воркером (буфер был заполнен за ~3-4 минуты):
1 веб-воркер


Точно таким же образом происходит отрисовка фрактала Ньютона на онлайн-демо. Однако, из-за того, что время обработки одного пикселя не зависит от его координат, все веб-воркеры завершают работу примерно в одно и то же время.
Вывод
Благодаря развитию современных браузеров, мы можем достигнуть, мало того, что около-нативной производительности с помощью WebAssembly, но и использовать аппаратные средства для ускорения вычислений.
Использовать SIMD команды может быть не всегда просто, но они могут увеличить скорость выполнения кода до 400%. Для использования мультипоточности процессора нужно организовывать систему обмена сообщений между потоками-воркерами. Вручную делать это достаточно трудозатратно, но зато при правильном разбиении задачи между потоками мы можем избавиться от состояния гонки за данными и свести на нет ожидания ядер процессора.
Конечно, навряд ли удастся достичь ускорения в
CORES_COUNT * REGISTERS_COUNT раз из-за программных и технических ограничений, но даже половина от этого произведения — существенный прирост.Ссылка на исходный код онлайн-демо.
Первая часть.

