
Есть тексты, похожие на вино или динамит: с годами они не стареют, а напротив, приобретают вес и значимость. Сегодня к старту флагманского курса о Data Science мы решили поделиться переводом визуального учебного руководства о NumPy 2019 года, прочитав которое даже не слишком близкий к математике человек поймёт, как работает эта библиотека Python. Если вы не хотите долго объяснять NumPy, но делать это всё равно приходится, положите статью в закладки и она сэкономит ваше время.
Пакет NumPy — это своего рода рабочая лошадка для анализа данных, машинного обучения и научных вычислений в экосистеме Python. Этот пакет значительно упрощает работу с векторами и матрицами. Многие популярные пакеты Python (например, scikit-learn, SciPy, pandas и tensorflow) включают NumPy в свою инфраструктуру в качестве основного элемента. Помимо возможности формирования продольных и поперечных срезов данных пакет NumPy позволяет отлаживать и запускать более сложные сценарии использования этих библиотек.
В данной статье мы рассмотрим некоторые основные способы применения NumPy, а также методы обработки и представления различных типов данных (таблиц, изображений, текста и пр.) для их последующей передачи в модели машинного обучения.
Начнём с установки [прим. ред. — несколько удивительно, что в оригинальной статье о ней ничего не сказано]:
pip install numpyИ импортируем пакет в Python, чтобы начать работу:
import numpy as npСоздание массивов
Массивы в NumPy (ndarray) создаются посредством передачи в NumPy списка Python в функцию np.array(). В нашем случае Python создаёт массив, показанный справа:

Часто бывает нужно, чтобы NumPy сам инициализировал значения массива. В NumPy для таких случаев предусмотрены особые методы, например ones(), zeros() и random.random(). Нужно просто сообщить этим методам количество элементов, которое необходимо сгенерировать:
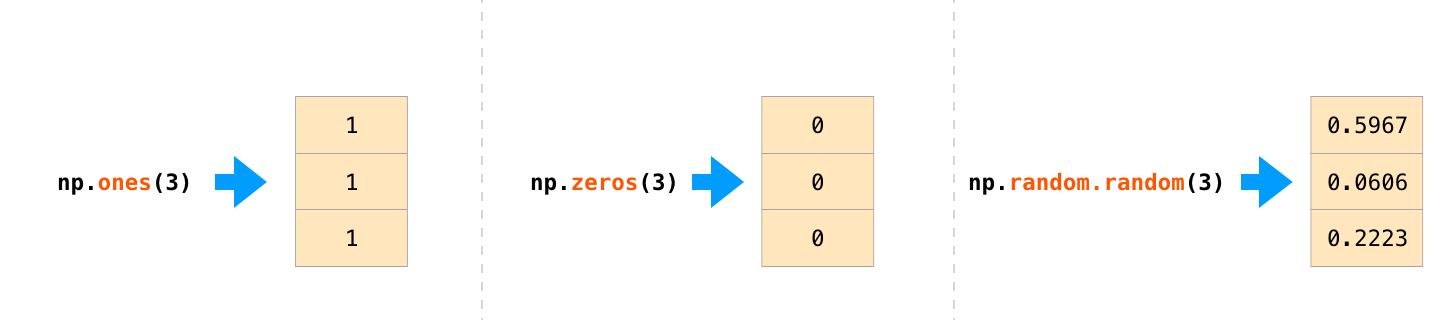
После создания массивов можно начинать с ними работать.
Арифметические операции над массивами данных
Создадим два массива NumPy и на их примере покажем преимущества пакета. Назовём массивы data и ones:

Просуммировать их по позициям (т. е. просуммировать значения каждой строки) очень просто: надо ввести команду data + ones:

Чем хороши такие инструменты? Тем, что такая абстракция позволяет избавиться от утомительного программирования циклов. Реализованный подход настолько замечателен, что высвобождает разум для размышлений о проблемах на более высоком уровне. Таким же образом можно выполнять не только операции сложения:

Часто возникают случаи, когда нужно выполнить арифметическое действие между всем массивом и одним числом (такую операцию назовём векторно-скалярной). Предположим, что в массиве представлены данные о расстоянии в милях, а мы хотим преобразовать эти данные в километры. Просто вводим команду data * 1.6:

NumPy сам понял, что умножить на указанное число нужно каждый элемент массива! Такая концепция называется транслированием, и она чрезвычайно удобна.
Индексирование
В NumPy индексировать и нарезать [более формально говорят "делать срез", а специалисты в Python называют срез слайсом] массивы можно всеми способами, которыми нарезаются списки Python:

Агрегирование
Реализована ещё одна полезная функция — агрегирование:

Кроме функций вычисления минимального, максимального значения и суммы (min, max и sum) можно воспользоваться такими замечательными функциями, как mean (для получения среднего значения), prod (для перемножения всех элементов), std (для вычисления стандартного отклонения), и множеством других.
А как обстоят дела с более высокими размерностями?
Во всех приведённых выше примерах использовались одномерные векторы. Но главная прелесть пакета NumPy заключается в его способности применять все описанные выше операции к любому количеству размерностей.
Создание матриц
Для того чтобы NumPy создал матрицу для представления списков из списков Python, мы можем передать такие списки в следующей форме:
np.array([[1,2],[3,4]])
А если передать в упомянутые выше методы (ones(), zeros() и random.random()) кортеж, описывающий размерность создаваемой матрицы, этими методами можно пользоваться точно так же, как для одномерных данных:

Арифметические операции над матрицами
Если две матрицы имеют одинаковую размерность, их можно складывать и перемножать с помощью арифметических операторов (+-*/). NumPy обрабатывает такие действия как позиционные операции:

Если матрицы имеют разную размерность, арифметические операции к ним можно применять, только если размерность одной из матриц равняется единице (например, матрица имеет только один столбец или одну строку), и в этом случае NumPy для данной операции использует собственные правила транслирования:

Скалярное произведение
Разновидностью арифметических операций является операция перемножения матриц с использованием функции скалярного произведения. Для выполнения в NumPy операции скалярного произведения над другими матрицами к каждой матрице применяется метод dot():

Внизу рисунка я указал размерности матриц, чтобы было понятно, что для выполнения операции обе матрицы должны иметь одинаковую размерность на "примыкающих" друг к другу сторонах. Наглядно это можно представить следующим образом:

Индексирование матриц
При работе с матрицами операции индексирования и нарезки становятся ещё более практичными:

Агрегирование матриц
Агрегирование матриц осуществляется точно так же, как агрегирование векторов:

Агрегировать можно не только все значения в матрице, но и значения по строкам или столбцам с помощью параметра axis:

Транспонирование и изменение формы матриц
При работе с матрицами часто возникает необходимость их поворота. Такой поворот (транспонирование) часто необходим, когда нужно взять скалярное произведение двух матриц и для этого привести их к общей размерности. Для транспонирования матрицы в массивах NumPy предусмотрено удобное свойство T:

В более сложных случаях может понадобиться переключение размерностей определённой матрицы. Необходимость в этом часто возникает в приложениях машинного обучения, когда определённая модель ожидает на входе определённую форму данных, но на вход поступает другая форма. Для таких случаев в NumPy предусмотрен метод reshape(). В этот метод нужно просто передать новые размерности матрицы. Если указать размерность -1, NumPy на основе вашей матрицы сможет определить правильную размерность:

А если размерности ещё более высокие?
NumPy может выполнять все вышеупомянутые операции с матрицами любой размерности. Не зря же основная структура данных NumPy называется n-мерным массивом (ndarray, N-Dimensional Array).

Часто ввести новую размерность можно простым добавлением запятой и числа к параметрам функции NumPy:

Примечание: следует отметить, что при распечатке трёхмерного массива NumPy выводимый текст отображается несколько иначе, чем показано здесь. n-мерные массивы в NumPy распечатываются таким образом, что в первую очередь осуществляется проход по элементам последней координаты матрицы, а в последнюю очередь — по первой. Другими словами, np.ones((4,3,2)) на распечатке будет выглядеть так:
array([[[1., 1.],
[1., 1.],
[1., 1.]],
[[1., 1.],
[1., 1.],
[1., 1.]],
[[1., 1.],
[1., 1.],
[1., 1.]],
[[1., 1.],
[1., 1.],
[1., 1.]]])
Применение на практике
Итак, что нам даёт этот пакет? Вот несколько полезных примеров применения NumPy.
Формулы
Основной областью применения NumPy является реализация математических формул, работающих с матрицами и векторами. Именно по этой причине с NumPy так любят работать члены научного сообщества Python. Возьмём, к примеру, главную для моделей машинного обучения формулу для расчёта среднеквадратичной погрешности, используемую при решении задач регрессии:

В NumPy эта формула реализуется очень просто:

Прелесть в том, что для NumPy не важно, содержат ли векторы predictions и labels одно или тысячу значений (главное, чтобы их размерности были одинаковыми). Рассмотрим пример более внимательно, последовательно выполнив четыре операции в этой строке кода:

Векторы predictions и labels содержат по три значения. Другими словами, n равняется 3. После выполнения операции вычитания получаем следующие значения:

Возведём в квадрат значения в векторе:

И суммируем эти значения:

В результате получаем значение погрешности для данного прогноза и оценку качества модели.
Представление данных
Представьте, какое множество типов данных вам, возможно, придётся обрабатывать и передавать в модели (электронные таблицы, изображения, аудио... и т. д.). Многие из таких данных идеально подходят для представления в n-мерном массиве:
Электронные таблицы
Электронная таблица, или таблица значений, представляет собой двумерную матрицу. Каждый лист в электронной таблице может представлять собой отдельную переменную. Наиболее популярной абстракцией в Python для них является объект pandas dataframe, фактически использующий NumPy и являющийся его надстройкой.

Аудио и временные ряды
Аудиофайл — это одномерный массив сэмплов. Каждый сэмпл — это число, представляющее собой крошечный фрагмент аудиосигнала. В аудио CD-качества могут содержаться до 44 100 сэмплов в секунду, каждый сэмпл представляет собой целое число от -32767 до 32768. Другими словами, если у вас есть десятисекундный WAVE-файл CD-качества, его можно загрузить в массив NumPy длиной 10 * 44100 = 441000 сэмплов. Хотите извлечь первую секунду звука? Просто загрузите файл в массив NumPy (назовём его audio) и напишите audio[:44100]. Вот так может выглядеть фрагмент аудиофайла:

Аналогичным образом NumPy поступает с данными временных рядов (например, с динамикой изменения цен на акции с течением времени).
Изображения
Изображение — это матрица пикселей размером (высота x ширина).
Если изображение чёрно-белое (в так называемой градации серого), каждый пиксель может быть представлен одним числом (обычно от 0 (чёрный) до 255 (белый)). Хотите получить срез верхней левой части изображения размером 10 x 10 пикселей? Просто выполните в NumPy этот код: image[:10,:10].
Вот так может выглядеть фрагмент файла изображения:

Если изображение цветное, каждый пиксель представляется тремя числами из красного, зелёного и синего спектральных цветов. В данном случае нам необходима третья размерность (так как каждая ячейка может содержать только одно число). Соответственно, цветное изображение представляется массивом размерностей: (высота x ширина x 3).

Текст
При работе с текстом ситуация несколько иная. Для числового представления текста сначала необходимо создать словарь (перечень всех уникальных слов, которые должна знать модель) и его векторное представление (первый этап). Попробуем представить в цифровой форме цитату из стихотворения, переведённую на английский язык:
“Have the bards who preceded me left any theme unsung?” (Оставили ли барды до меня какой-то из предметов невоспетым?)
Перед переводом этого предложения в нужную цифровую форму модель должна проанализировать огромное количество текста. Отправим в модель на обработку небольшой набор данных и используем его для создания словаря (из 71290 слов):

После этого разобьём предложение на массив лексем (слов или частей слов, основанных на общих правилах):

Затем заменим каждое слово его идентификатором в словарной таблице:

Однако для работы модели такие идентификаторы не годятся. Поэтому перед передачей последовательности слов в модель лексемы/слова должны быть заменены их векторными представлениями (в данном случае используется 50-мерное векторное представление word2vec):

Очевидно, что этот массив NumPy имеет следующие размерности [embedding_dimension x sequence_length]. В реальности всё выглядит несколько иначе, однако данное визуальное представление более наглядно отражает общие принципы. По соображениям производительности модели глубокого обучения, как правило, сохраняют первую размерность для пакета (поскольку модель обучается быстрее на нескольких параллельных примерах). Именно в таких случаях может оказаться полезной функция reshape(). В модель типа BERT, к примеру, данные будут вводиться в следующей форме: [batch_size, sequence_length, embedding_size].
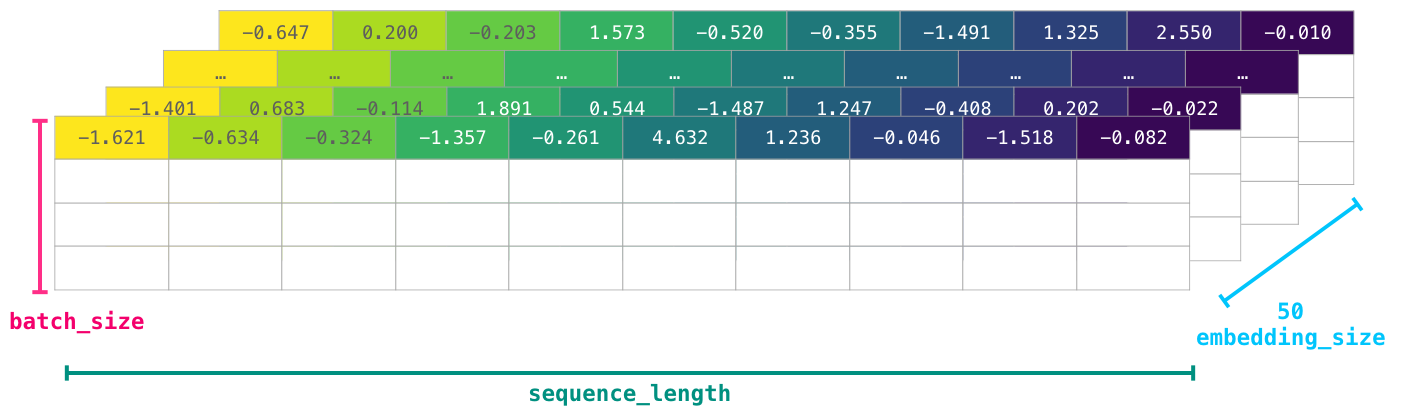
В результате мы получили числовой том, с которым может работать модель. Некоторые строки я оставил пустыми, однако их можно заполнить другими примерами, на которых может тренироваться модель (или делать прогнозы).
Поэма, строка из которой была использована в примере, увековечила своего автора, Антара ибн Шаддада, незаконнорождённого сына главы племени от чернокожей рабыни, мастерски владевшего языком поэзии. Вокруг этой исторической фигуры сложились мифы и легенды, а его стихи стали частью классической арабской литературы).
Специалисты в Data Science называют науку о данных очень визуальной областью. Действительно, лучший способ в том или ином смысле оценить данные и понять, какую пользу можно из них извлечь — это визуализация, потому что именно она помогает воспринимать даннные как целое, при этом учитывая детали. Если вы хотите чётко представлять, как наука о данных рабтоает изнутри, то вы можете присмотреться к нашему курсу, студенты которого за время обучения получают опыт, эквивалентный трём годам самостоятельных поисков и усилий в Data Science.

Узнайте, как прокачаться и в других специальностях или освоить их с нуля:
Другие профессии и курсы
ПРОФЕССИИ
КУРСЫ
