Сегодня поговорим о фонтанных кодах. Их ещё называют «кодами нефиксированной скорости». Фонтанный код позволяет взять, например, какой-нибудь файл, и преобразовать его в практически неограниченное количество закодированных блоков. Имея некоторое подмножество этих блоков, можно восстановить исходный файл, при условии, что размер этого подмножества немного превышает размер файла. Другими словами, такой код позволяет создавать «фонтан» из кодируемых данных. Получатель может восстановить исходные данные, собрав достаточно «капель» из фонтана, при этом неважно – какие именно «капли» у него есть, и какие именно он пропустил.

Замечательное свойство фонтанных кодов заключается в том, что их применение позволяет отправлять данные по ненадёжным каналам связи, например – через интернет, не полагаясь на знание уровня потери пакетов, и не требуя от получателя связываться с отправителем для восстановления недостающих фрагментов данных. Легко заметить, что подобные возможности окажутся весьма кстати во множестве ситуаций. Среди них, например, отправка информации по широковещательным каналам связи, как в системах передачи видео по запросу. К той же категории задач относится работа протокола Bittorrent и других подобных, когда фрагменты файла распространяются среди большого количества пиров.
Может показаться, что фонтанные коды должны быть устроены ужасно сложно. Но это вовсе не так. Существуют разные реализации этого алгоритма, мы предлагаем начать с самой простой из них. Это – так называемый код преобразования Лаби, сокращённо его обычно называют LT-кодом, от Luby Transform Сode. При использовании этого варианта фонтанных кодов блоки кодируют так:
Как видите, тут нет ничего сложного. Но надо отметить, что многое в этой схеме зависит от так называемого распределения степеней кодовых символов, от того, как выбирают количество блоков, которые нужно скомбинировать. К этому вопросу мы ещё вернёмся. Из описания можно заметить, что некоторые из закодированных блоков, фактически, созданы с использованием лишь одного блока исходных данных, в то время как в кодировании большинства блоков задействованы несколько исходных блоков.
Вот ещё одна особенность кодирования, не вполне очевидная с первого взгляда. Заключается она в том, что до тех пор, пока мы позволяем получателю знать то, какие именно блоки мы комбинируем для того, чтобы получить выходной блок, нам не нужно в явном виде передавать этот список. Если отправитель и получатель договорятся о некоем генераторе псевдослучайных чисел, можно инициализировать генератор случайно выбранным числом и использовать для выбора распределения степеней и набора исходных блоков. Начальное число просто отправляют вместе с закодированным блоком, а получатель может использовать для восстановления списка исходных блоков ту же самую процедуру, что использовал отправитель при кодировании.
Процедура декодирования немного сложнее, хотя она тоже достаточно проста.
Рассмотрим пример декодирования для того, чтобы лучше во всём разобраться. Предположим, мы получили пять закодированных блоков, каждый – длиной один байт. Так же получены сведения о том, из каких исходных блоков каждый из них сконструирован. Эти данные можно представить в виде графа.
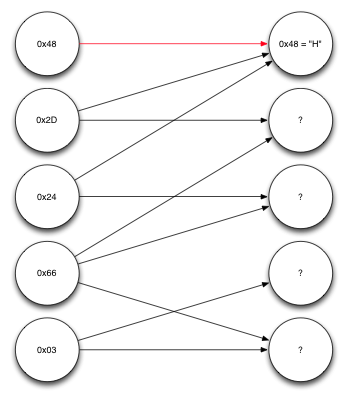
Граф, представляющий полученные данные
Узлы слева представляют собой полученные закодированные блоки. Узлы справа – исходные блоки. Первый из полученных блоков, 0x48, как оказалось, сформирован при участии лишь одного исходного блока, первого. Таким образом, мы уже знаем, что это был за блок. Переходя в обратном направлении по стрелкам, указывающим на первый исходный блок, видим, что второй и третий закодированные блоки зависят только от первого исходного блока и от одного другого. А, так как первый исходный блок уже известен, можем произвести над полученными блоками и первым исходным блоком операцию XOR и раскодировать ещё несколько блоков.
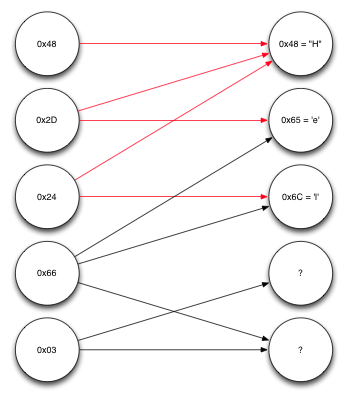
Продолжение декодирования сообщения
Повторяя снова ту же самую процедуру, можно заметить, что теперь известно достаточно для декодирования четвёртого блока, который зависит от второго и третьего исходных блоков, каждый из которых уже раскодирован. Выполнение над ними операции XOR позволяет найти пятый, то есть, последний в списке исходные блок, что показано на рисунке ниже.
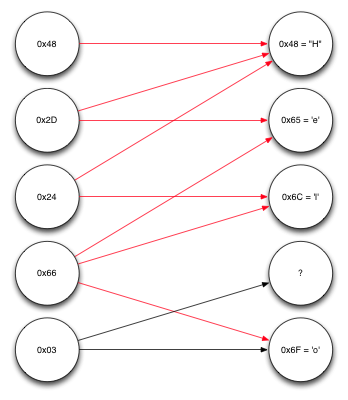
Декодированный пятый исходный блок
И, наконец, теперь можно декодировать последний из оставшихся исходных блоков, что, в итоге, даст сообщение, которое отправитель хотел передать получателю.
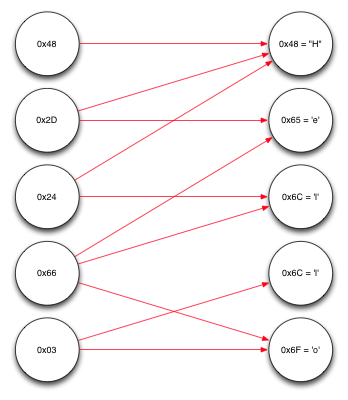
Полностью декодированное сообщение
Надо признать, что пример это искусственный. Здесь мы исходим из предположения, что получены только блоки, необходимые для декодирования исходного сообщения. К тому же, среди блоков нет ничего лишнего, а сами блоки расположены в весьма удобном порядке. Но это –лишь демонстрация принципов работы фонтанных кодов. Мы уверены, что вы, благодаря этому примеру, сможете понять, как те же самые процедуры работают с более крупными блоками и более длинными файлами.
Ранее было сказано, что то, как выбирают количество исходных блоков, из которых должен состоять каждый из закодированных блоков, или распределение степеней кодовых символов, очень важно. И, на самом деле, так оно и есть. В идеале алгоритм должен генерировать небольшое количество закодированных блоков, для создания которых используется лишь один исходный блок. Нужно это для того, чтобы получатель мог приступить к раскодированию сообщения. При этом большинство закодированных блоков должно зависеть от небольшого количества других блоков. Всё дело – в правильном подборе распределения. Подобное распределение, отлично подходящее для наших целей, существует. Называется оно идеальным распределением солитона.
К сожалению, на практике это распределение не такое уж и идеальное. Дело в том, что случайные вариации приводят к тому, что некоторые блоки источника не используются, или к тому, что декодирование стопорится, когда у декодера заканчиваются известные блоки. Один из вариантов такого распределения, называемый робастным распределением солитона, позволяет улучшить показатели алгоритма, генерируя больше блоков из очень малого количества исходных блоков, а также генерируя некоторые блоки, которые являются комбинацией всех или почти всех исходных блоков. Делается это для облегчения декодирования некоторого количества последних блоков.
Вот, вкратце, как работают фонтанные коды, и, в частности, LT-коды. Надо сказать, что LT-коды – это наименее эффективные из известных фонтанных кодов, но они – и самые простые для понимания.
Прежде чем мы окончим этот разговор, вот ещё одна мысль. Фонтанные коды могут выглядеть идеально для систем вроде Bittorrent, позволяя сидам генерировать и распространять практически неограниченное количество блоков, более или менее исключая проблему «последнего блока» в случаях, когда сидов немного, и обеспечивая то, что два случайно выбранных пира практически всегда обладают полезной информацией, которой могут друг с другом обмениваться. Однако, тут есть одна важная проблема. Дело в том, что очень сложно проверить данные, полученные от пиров.
Пиринговые протоколы используют функции безопасного хеширования, вроде SHA1, при этом доверенная сторона, создатель раздачи, предоставляет список достоверных хешей всем пирам. Каждый пир, пользуясь этими данными, может проверить загружаемые фрагменты файла. Однако, при использовании фонтанных кодов подобная схема работы усложняется. Нет способа вычислить, например, хеш SHA1 закодированного фрагмента, даже зная хеши отдельных фрагментов, которые приняли участие в его формировании. И мы не можем доверять другим пирам вычисление этого хеша за нас, так как они могут попросту нас обмануть. Мы можем подождать, пока соберём весь файл, а затем, пользуясь списком неправильных фрагментов, можем попытаться найти неверные закодированные фрагменты, но это сложно и ненадёжно. К тому же, при таком подходе, найти ошибки можно только в финале сборки файла, то есть – это, скорее всего, займёт слишком много времени. Одна из возможных альтернатив заключается в том, чтобы создатель раздачи опубликовал открытый ключ и подписывал каждый сгенерированный блок. Таким образом мы можем проверить закодированные блоки, но и тут есть серьёзный минус. Дело в том, что только создатель раздачи может генерировать правильные блоки, а значит мы сразу же теряем большинство преимуществ использования фонтанных кодов. Кажется, тут мы зашли в тупик. Однако, имеются альтернативы, например, весьма хитроумная схема, называемая гомоморфным хешированием. Хотя и она не идеальна.
Мы рассказали об основах фонтанных кодов. Разновидности этого алгоритма нашли практическое применение в тех областях, где его достоинства однозначно перевешивают недостатки. Если эта тема вас заинтересовала и вы хотите в неё углубиться, почитайте этот материал по фонтанным кодам. Кроме того, полезно будет ознакомиться с Raptor-кодами, которые, немного усложняя LT-коды, значительно улучшают их эффективность. Благодаря их использованию можно снизить объёмы передаваемых данных и вычислительную сложность алгоритма.

Замечательное свойство фонтанных кодов заключается в том, что их применение позволяет отправлять данные по ненадёжным каналам связи, например – через интернет, не полагаясь на знание уровня потери пакетов, и не требуя от получателя связываться с отправителем для восстановления недостающих фрагментов данных. Легко заметить, что подобные возможности окажутся весьма кстати во множестве ситуаций. Среди них, например, отправка информации по широковещательным каналам связи, как в системах передачи видео по запросу. К той же категории задач относится работа протокола Bittorrent и других подобных, когда фрагменты файла распространяются среди большого количества пиров.
Основные принципы
Может показаться, что фонтанные коды должны быть устроены ужасно сложно. Но это вовсе не так. Существуют разные реализации этого алгоритма, мы предлагаем начать с самой простой из них. Это – так называемый код преобразования Лаби, сокращённо его обычно называют LT-кодом, от Luby Transform Сode. При использовании этого варианта фонтанных кодов блоки кодируют так:
- Выбирают из диапазона 1 — k случайное число d. Диапазон соответствует количеству блоков в файле. Ниже мы поговорим о том, как лучше всего выбрать d.
- Выбирают случайным образом d блоков файла и комбинируют их. В нашем случае хорошо подойдёт операция XOR.
- Передают полученный на предыдущем шаге блок вместе с информацией о том, из каких блоков он был создан.
Как видите, тут нет ничего сложного. Но надо отметить, что многое в этой схеме зависит от так называемого распределения степеней кодовых символов, от того, как выбирают количество блоков, которые нужно скомбинировать. К этому вопросу мы ещё вернёмся. Из описания можно заметить, что некоторые из закодированных блоков, фактически, созданы с использованием лишь одного блока исходных данных, в то время как в кодировании большинства блоков задействованы несколько исходных блоков.
Вот ещё одна особенность кодирования, не вполне очевидная с первого взгляда. Заключается она в том, что до тех пор, пока мы позволяем получателю знать то, какие именно блоки мы комбинируем для того, чтобы получить выходной блок, нам не нужно в явном виде передавать этот список. Если отправитель и получатель договорятся о некоем генераторе псевдослучайных чисел, можно инициализировать генератор случайно выбранным числом и использовать для выбора распределения степеней и набора исходных блоков. Начальное число просто отправляют вместе с закодированным блоком, а получатель может использовать для восстановления списка исходных блоков ту же самую процедуру, что использовал отправитель при кодировании.
Процедура декодирования немного сложнее, хотя она тоже достаточно проста.
- Восстановить список исходных блоков, которые были использованы для создания закодированного блока.
- Для каждого исходного блока из этого списка, если уже его декодировали, произвести операцию XOR с закодированным блоком и убрать его из списка исходных блоков.
- Если в списке остались как минимум два исходных блока, добавить закодированный блок в область временного хранения.
- Если в списке остался лишь один исходный блок, это значит, что очередной исходный блок успешно декодирован! Его нужно добавить к декодированному файлу и пройтись по списку временного хранения, повторяя эту процедуру для любых исходных блоков, которые содержат найденный блок.
0x48 0x65 0x6C 0x6C 0x6F, world!
Рассмотрим пример декодирования для того, чтобы лучше во всём разобраться. Предположим, мы получили пять закодированных блоков, каждый – длиной один байт. Так же получены сведения о том, из каких исходных блоков каждый из них сконструирован. Эти данные можно представить в виде графа.
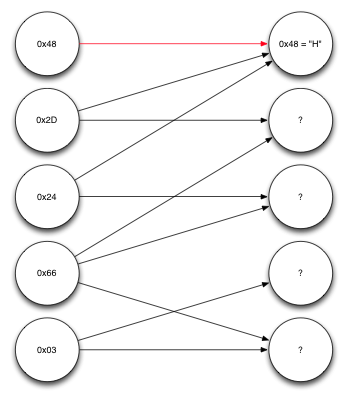
Граф, представляющий полученные данные
Узлы слева представляют собой полученные закодированные блоки. Узлы справа – исходные блоки. Первый из полученных блоков, 0x48, как оказалось, сформирован при участии лишь одного исходного блока, первого. Таким образом, мы уже знаем, что это был за блок. Переходя в обратном направлении по стрелкам, указывающим на первый исходный блок, видим, что второй и третий закодированные блоки зависят только от первого исходного блока и от одного другого. А, так как первый исходный блок уже известен, можем произвести над полученными блоками и первым исходным блоком операцию XOR и раскодировать ещё несколько блоков.
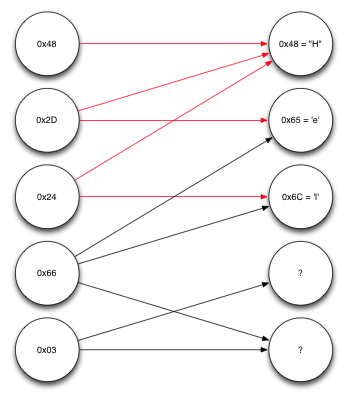
Продолжение декодирования сообщения
Повторяя снова ту же самую процедуру, можно заметить, что теперь известно достаточно для декодирования четвёртого блока, который зависит от второго и третьего исходных блоков, каждый из которых уже раскодирован. Выполнение над ними операции XOR позволяет найти пятый, то есть, последний в списке исходные блок, что показано на рисунке ниже.

Декодированный пятый исходный блок
И, наконец, теперь можно декодировать последний из оставшихся исходных блоков, что, в итоге, даст сообщение, которое отправитель хотел передать получателю.

Полностью декодированное сообщение
Надо признать, что пример это искусственный. Здесь мы исходим из предположения, что получены только блоки, необходимые для декодирования исходного сообщения. К тому же, среди блоков нет ничего лишнего, а сами блоки расположены в весьма удобном порядке. Но это –лишь демонстрация принципов работы фонтанных кодов. Мы уверены, что вы, благодаря этому примеру, сможете понять, как те же самые процедуры работают с более крупными блоками и более длинными файлами.
Об идеальном распределении
Ранее было сказано, что то, как выбирают количество исходных блоков, из которых должен состоять каждый из закодированных блоков, или распределение степеней кодовых символов, очень важно. И, на самом деле, так оно и есть. В идеале алгоритм должен генерировать небольшое количество закодированных блоков, для создания которых используется лишь один исходный блок. Нужно это для того, чтобы получатель мог приступить к раскодированию сообщения. При этом большинство закодированных блоков должно зависеть от небольшого количества других блоков. Всё дело – в правильном подборе распределения. Подобное распределение, отлично подходящее для наших целей, существует. Называется оно идеальным распределением солитона.
К сожалению, на практике это распределение не такое уж и идеальное. Дело в том, что случайные вариации приводят к тому, что некоторые блоки источника не используются, или к тому, что декодирование стопорится, когда у декодера заканчиваются известные блоки. Один из вариантов такого распределения, называемый робастным распределением солитона, позволяет улучшить показатели алгоритма, генерируя больше блоков из очень малого количества исходных блоков, а также генерируя некоторые блоки, которые являются комбинацией всех или почти всех исходных блоков. Делается это для облегчения декодирования некоторого количества последних блоков.
Вот, вкратце, как работают фонтанные коды, и, в частности, LT-коды. Надо сказать, что LT-коды – это наименее эффективные из известных фонтанных кодов, но они – и самые простые для понимания.
Пиринговые сети и проблема доверия
Прежде чем мы окончим этот разговор, вот ещё одна мысль. Фонтанные коды могут выглядеть идеально для систем вроде Bittorrent, позволяя сидам генерировать и распространять практически неограниченное количество блоков, более или менее исключая проблему «последнего блока» в случаях, когда сидов немного, и обеспечивая то, что два случайно выбранных пира практически всегда обладают полезной информацией, которой могут друг с другом обмениваться. Однако, тут есть одна важная проблема. Дело в том, что очень сложно проверить данные, полученные от пиров.
Пиринговые протоколы используют функции безопасного хеширования, вроде SHA1, при этом доверенная сторона, создатель раздачи, предоставляет список достоверных хешей всем пирам. Каждый пир, пользуясь этими данными, может проверить загружаемые фрагменты файла. Однако, при использовании фонтанных кодов подобная схема работы усложняется. Нет способа вычислить, например, хеш SHA1 закодированного фрагмента, даже зная хеши отдельных фрагментов, которые приняли участие в его формировании. И мы не можем доверять другим пирам вычисление этого хеша за нас, так как они могут попросту нас обмануть. Мы можем подождать, пока соберём весь файл, а затем, пользуясь списком неправильных фрагментов, можем попытаться найти неверные закодированные фрагменты, но это сложно и ненадёжно. К тому же, при таком подходе, найти ошибки можно только в финале сборки файла, то есть – это, скорее всего, займёт слишком много времени. Одна из возможных альтернатив заключается в том, чтобы создатель раздачи опубликовал открытый ключ и подписывал каждый сгенерированный блок. Таким образом мы можем проверить закодированные блоки, но и тут есть серьёзный минус. Дело в том, что только создатель раздачи может генерировать правильные блоки, а значит мы сразу же теряем большинство преимуществ использования фонтанных кодов. Кажется, тут мы зашли в тупик. Однако, имеются альтернативы, например, весьма хитроумная схема, называемая гомоморфным хешированием. Хотя и она не идеальна.
Заключение
Мы рассказали об основах фонтанных кодов. Разновидности этого алгоритма нашли практическое применение в тех областях, где его достоинства однозначно перевешивают недостатки. Если эта тема вас заинтересовала и вы хотите в неё углубиться, почитайте этот материал по фонтанным кодам. Кроме того, полезно будет ознакомиться с Raptor-кодами, которые, немного усложняя LT-коды, значительно улучшают их эффективность. Благодаря их использованию можно снизить объёмы передаваемых данных и вычислительную сложность алгоритма.
О, а приходите к нам работать? :)wunderfund.io — молодой фонд, который занимается высокочастотной алготорговлей. Высокочастотная торговля — это непрерывное соревнование лучших программистов и математиков всего мира. Присоединившись к нам, вы станете частью этой увлекательной схватки.
Мы предлагаем интересные и сложные задачи по анализу данных и low latency разработке для увлеченных исследователей и программистов. Гибкий график и никакой бюрократии, решения быстро принимаются и воплощаются в жизнь.
Присоединяйтесь к нашей команде: wunderfund.io