Комментарии 52
НЛО прилетело и опубликовало эту надпись здесь
Крайне зачётная статья! Спасибо за труд.
НЛО прилетело и опубликовало эту надпись здесь
Да, по первому пункту согласен, скорее всего в процессе редактирования напортачил, сейчас поправлю.
Насчёт второго пункта — серая полоса на графика показывает сигнал с уровнем 1. И я тоже считал, что эти фильтры не должны вызывать усиления сигнала, однако именно такой график получается, если брать информацию из BiquadFilterNode#getFrequencyResponse. Либо это ошибка в реализации данной функции, либо сам фильтр действительно так устроен, тестов пока не проводил. Вообще этот график сильно похож на график групповой задержки для фильтра Баттерворта (https://ru.wikipedia.org/wiki/%D0%A4%D0%B8%D0%BB%D1%8C%D1%82%D1%80_%D0%91%D0%B0%D1%82%D1%82%D0%B5%D1%80%D0%B2%D0%BE%D1%80%D1%82%D0%B0)
Насчёт второго пункта — серая полоса на графика показывает сигнал с уровнем 1. И я тоже считал, что эти фильтры не должны вызывать усиления сигнала, однако именно такой график получается, если брать информацию из BiquadFilterNode#getFrequencyResponse. Либо это ошибка в реализации данной функции, либо сам фильтр действительно так устроен, тестов пока не проводил. Вообще этот график сильно похож на график групповой задержки для фильтра Баттерворта (https://ru.wikipedia.org/wiki/%D0%A4%D0%B8%D0%BB%D1%8C%D1%82%D1%80_%D0%91%D0%B0%D1%82%D1%82%D0%B5%D1%80%D0%B2%D0%BE%D1%80%D1%82%D0%B0)
Используя webaudioplayground.appspot.com (спасибо dtestyk) Воспроизвёл поведение данного фильтра:
Создаём такую схему: Oscillator node -> Biquad filter (lowpass, Q=15, freq=5000) -> Analyzer -> выход
Запускаем воспроизведение в oscilator'е и меняем частоту. В районе 5000 Hz отчётливо слышно и видно резкое усиление звука.
Так что данные графики отображают действительную картину того, как работает фильтр lowpass в web audio api.
Создаём такую схему: Oscillator node -> Biquad filter (lowpass, Q=15, freq=5000) -> Analyzer -> выход
Запускаем воспроизведение в oscilator'е и меняем частоту. В районе 5000 Hz отчётливо слышно и видно резкое усиление звука.
Так что данные графики отображают действительную картину того, как работает фильтр lowpass в web audio api.
И да, стоит добавить, что если говорить о цифровом сигнале, что точно восстановить из него аналоговый может не получиться даже, если частота дискретизации выше частоты Найквиста, т.к. есть ещё искажения сигнала связанные с его квантованием по уровню. Однако, нижняя граница частоты дискретизации всё равно не меняется.
НЛО прилетело и опубликовало эту надпись здесь
Да, но нет.
Можно взять конечный по времени сигнал, периодически его продолжить и применить теорему Котельникова. (Правда, придётся работать в обобщённых функциях.) Это снимет все перечисленные недостатки (бесконечное число отсчетов, бесконечная задержка, etc — отсчёты-то повторяются). Но «работать» от этого теорема Котельникова не начнёт, поскольку восстановить по ней сигнал может только математик формулами на бумаге, а реальный ЦАП ничего и близко похожего на процедуру восстановления сигнала по Котельникову выдать не может.
Подумываю написать статью «Легенды и мифы о теореме Котельникова».
Можно взять конечный по времени сигнал, периодически его продолжить и применить теорему Котельникова. (Правда, придётся работать в обобщённых функциях.) Это снимет все перечисленные недостатки (бесконечное число отсчетов, бесконечная задержка, etc — отсчёты-то повторяются). Но «работать» от этого теорема Котельникова не начнёт, поскольку восстановить по ней сигнал может только математик формулами на бумаге, а реальный ЦАП ничего и близко похожего на процедуру восстановления сигнала по Котельникову выдать не может.
Подумываю написать статью «Легенды и мифы о теореме Котельникова».
Теорема Котельникова — это математическая теорема ) У нее не может быть «недостатков», поскольку она математически верна (строго доказана). Проблемы применение мат аппарата к решению каких-то прикладных задач — это проблемы самих прикладных задач. Поэтому говорить, что " у теоремы есть определенные недостатки" или «она работает, хотя и плоховато» как-то несколько неправильно ).
может кому будет полезно:
toxicdump.org/stuff/FourierToy.swf визуализация синусоид
bfxr.net генерация с множеством параметров
text programming sound synthesis:
wavepot.com
studio.substack.net
wurstcaptures.untergrund.net/music
visual block playground:
webaudioplayground.appspot.com
app.hya.io
языки программирования звука:
pure data графический
ChucK текстовый
toxicdump.org/stuff/FourierToy.swf визуализация синусоид
bfxr.net генерация с множеством параметров
text programming sound synthesis:
wavepot.com
studio.substack.net
wurstcaptures.untergrund.net/music
visual block playground:
webaudioplayground.appspot.com
app.hya.io
языки программирования звука:
pure data графический
ChucK текстовый
Еще бы вы в яндекс радио нормализовали уровень громкости рекламы.
работаем над этим
Раз пошла такая пьянка про хотелки в Яндекс.музыке, то сделайте пожалуйста кнопку «Избранные» жанры, доступные со стартового.
Чаще всего слушаю «Энергичное» — оно как-то больше всего подходит, но он постоянно в самом конце длинного списка «Настроение», и очень редко, когда программа предлагает послушать этот жанр с первой страницы… А так — добавил в избранное и всегда где-то в быстром запуске.
2) Ну и дополню — я забиндил вашу прогу как программу по умолчанию в качестве музыки в Android'е, стоп/пауза и Next работают, а вот «холодный старт» нет. Т.е. нельзя просто с гарнитуры нажать «Play» и начать слушать музыку — приложение Стартует, но просит выбрать жанр. Т.е. просто начать слушать с гарнитуры нельзя.
3) Очень мало песен в стиле «Русский рэп». Иногда настроение такое, что хочется послушать жесткого гопо-рэпа, а там… всякие сопливые «тимати» и ко)) и почти нет Касты. АК47, Centr итд…
Чаще всего слушаю «Энергичное» — оно как-то больше всего подходит, но он постоянно в самом конце длинного списка «Настроение», и очень редко, когда программа предлагает послушать этот жанр с первой страницы… А так — добавил в избранное и всегда где-то в быстром запуске.
2) Ну и дополню — я забиндил вашу прогу как программу по умолчанию в качестве музыки в Android'е, стоп/пауза и Next работают, а вот «холодный старт» нет. Т.е. нельзя просто с гарнитуры нажать «Play» и начать слушать музыку — приложение Стартует, но просит выбрать жанр. Т.е. просто начать слушать с гарнитуры нельзя.
3) Очень мало песен в стиле «Русский рэп». Иногда настроение такое, что хочется послушать жесткого гопо-рэпа, а там… всякие сопливые «тимати» и ко)) и почти нет Касты. АК47, Centr итд…
Какая куча ошибок…
Начнем с простого:
ага. PCM.
А вот это уже DPCM.
Здесь-же прекрасно почти всё…
PCM в mp3 ??? Это как?
WAV, WMA, OGG — это не форматы. Это контейнеры. Тот-же WAV может содержать внутри как PCM, так и mp3
А вот PCM WAV это уже конкретный формат, а никак не контейнер…
Начнем с простого:
Самым распространённым из них является импульсно-кодовая модуляция,
ага. PCM.
при которой записывается не конкретное значение уровня сигнала в каждый момент времени, а разница между текущим и предыдущим значением. Это позволяет снизить количество бит на каждый отсчёт примерно на 25%.
А вот это уже DPCM.
Этот способ кодирования применяется в наиболее распространённых аудио-форматах (WAV, MP3, WMA, OGG, FLAC, APE), которые используют контейнер PCM WAV.
Здесь-же прекрасно почти всё…
PCM в mp3 ??? Это как?
WAV, WMA, OGG — это не форматы. Это контейнеры. Тот-же WAV может содержать внутри как PCM, так и mp3
А вот PCM WAV это уже конкретный формат, а никак не контейнер…
А когда в Яндекс.Музыке можно будет ожидать «похожее по исполнеНЕНИЮ». Чтобы можно было начать слушать любой трек и дальше слушать любых исполнителей схожих по звучанию? Даже если слушать радио по определенному жанру, там ну очень все разнообразное и такое ощущение, что просто собираются исполнители у которых тег = жанру, даже если это фактически не так. Искать не по исполнителю, не жанру, а именно звучанию. Или это какой-то космос в плане технологий и «харя треснет»?)
Космос. Лучшее что можно предложить это релейтед с ластфм, ну и у них база самая большая для построения подобного (у айтюнса конечно больше, но они особо не занимаются этим :)).
Релейтед с ластфм работает примерно так же хорошо как «с этим товаром часто покупают». То есть чуть лучше, чем никак.
Теоретически, должно быть вполне возможно машинно проанализировать музыку по каким-то ключевым параметрам. А если к этому добавить тегирование не только по жанру, но и, например, по «составу» (хотя бы на уровне вокал есть/нет, ключевой инструмент, тип состава (соло/дуэт/группа/камерный оркестр/симфонический оркестр)), то можно выдавать действительно похожую музыку. Конечно, тегирование по составу машина сделать вряд ли сможет, но так и жанры пока что «руками» определяются.
Теоретически, должно быть вполне возможно машинно проанализировать музыку по каким-то ключевым параметрам. А если к этому добавить тегирование не только по жанру, но и, например, по «составу» (хотя бы на уровне вокал есть/нет, ключевой инструмент, тип состава (соло/дуэт/группа/камерный оркестр/симфонический оркестр)), то можно выдавать действительно похожую музыку. Конечно, тегирование по составу машина сделать вряд ли сможет, но так и жанры пока что «руками» определяются.
существуют высокоуровневые признаки:
- energy
- dancibility
- hotttnesss
- duration
- speechiness
- acousticness
- liveness
- tempo
- ...
dancibility
Пожалуй, самый спорный признак. А именно, послушайте музыку (но не смотрите постановку) из танца Монтекки и Капулетти из балета «Ромэо и Джульетта» С. Прокофьева. Знаменитая музыкальная тема, мощная и энергичная. dancibility? Ау, это балет, оно делалось для танца.
И теперь если вы не видели балет, вы не догадаетесь даже примерно, как выглядит этот танец.
НЛО прилетело и опубликовало эту надпись здесь
Сумбурная и непоследовательная статья. Как и большинство подобных статей. Вот характерные признаки:
— пишут про теорему Котельникова: можно восстановить по отсчётам. И всё. Как потом восстановить — ни слова, и далёкие от математики читатели себе выдумывают «лесенку», потом им она не нравится, начинается — линейная интерполяция, квадратичная, кубическая… А потом видим утверждения (было и прямо на Хабре), что при восстановлении из отсчётов -1, 0, +1, 0, -1, 0, +1, 0,… в результате сигнал получается треугольный. Ну или что восстановленный по отсчётам 0, 0, 1, 1, 0, 0, 1, 1,… сигнал окажется меандром. А это совершенно не так, если мы говорим о теореме, потому, что как треугольник, так и меандр заведомо не являются ограниченными по частоте, не удовлетворяют её условию, поэтому не могли быть теми функциями, из которых мы получили отсчёты, и следовательно не могут получиться и в резульате восстановления по этим отсчётам.
А ведь достаточно было написать формулу для восстановления:
и всё, сразу видно: отсчётов нам нужно бесконечное количество, для восстановления почти в каждой точке нужно использовать сразу все отсчёты, а восстановленная функция в любом случае будет гладкой, не будет содержать никаких «острых углов». А если кто не знает, sinc(x)=sin(x)/x. То есть, как обычно, это математическая идеализация, непосредственно не применимая на практике, и для использования нужно строить с её помощью какие-то практически реализуемые конструкции.
— пишут про преобразование Фурье (даже не упоминая, что имеют ввиду именно дискретное преобразование). А то и сразу про БПФ, вроде как про серебрянную пулю (опять, имея ввижу исключительно алгоритм Cooley–Tukey и его требование, чтобы число отсчётов было степенью 2, хотя это — не единственный алгоритм БПФ, и у других такого жёсткого требования нет). А иногда речь на самом деле идёт про косинусное преобразование (частный случай, применяется в JPEG и т. д.).
И всё, что говорится про него — «разделяет сигнал на частоты». В чём заключается преобразование, что получается в результате, про оконирование — ни слова. А тут опять дьявол — в деталях. Формулы-то преобразования туда и обратно несложные, казалось бы, почему бы не выписать их? И сразу же станет видно, что результат преобразования — набор комплексных чисел и не всё там так просто.
— пишут про фильтры. Тут вообще атас, утверждения, что обрезные, шельфовые, полосовые фильтры делаются с помощью преобразования Фурье. Простой же вопрос — откуда тогда там появляется переменнй сдвиг фаз, если мы в образе были вольные его не вносить — не возникает ни у написателя статьи, ни у аудитории.
Ответ на этот вопрос очень прост: никто не реализует фильтр с помощью преобразования Фурье. Есть такие штуки — фильтры КИХ и фильтры БИХ, у каждого из них свои особенности, вот их-то все и используют. Сдвиг фаз как раз является следствием применения таких фильтров.
Куда было бы от вашей статьи больше пользы, если бы вы про Web Audio API рассказали подробнее, а не повторяли плохое изложение основ цифрового звука.
— пишут про теорему Котельникова: можно восстановить по отсчётам. И всё. Как потом восстановить — ни слова, и далёкие от математики читатели себе выдумывают «лесенку», потом им она не нравится, начинается — линейная интерполяция, квадратичная, кубическая… А потом видим утверждения (было и прямо на Хабре), что при восстановлении из отсчётов -1, 0, +1, 0, -1, 0, +1, 0,… в результате сигнал получается треугольный. Ну или что восстановленный по отсчётам 0, 0, 1, 1, 0, 0, 1, 1,… сигнал окажется меандром. А это совершенно не так, если мы говорим о теореме, потому, что как треугольник, так и меандр заведомо не являются ограниченными по частоте, не удовлетворяют её условию, поэтому не могли быть теми функциями, из которых мы получили отсчёты, и следовательно не могут получиться и в резульате восстановления по этим отсчётам.
А ведь достаточно было написать формулу для восстановления:
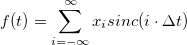и всё, сразу видно: отсчётов нам нужно бесконечное количество, для восстановления почти в каждой точке нужно использовать сразу все отсчёты, а восстановленная функция в любом случае будет гладкой, не будет содержать никаких «острых углов». А если кто не знает, sinc(x)=sin(x)/x. То есть, как обычно, это математическая идеализация, непосредственно не применимая на практике, и для использования нужно строить с её помощью какие-то практически реализуемые конструкции.— пишут про преобразование Фурье (даже не упоминая, что имеют ввиду именно дискретное преобразование). А то и сразу про БПФ, вроде как про серебрянную пулю (опять, имея ввижу исключительно алгоритм Cooley–Tukey и его требование, чтобы число отсчётов было степенью 2, хотя это — не единственный алгоритм БПФ, и у других такого жёсткого требования нет). А иногда речь на самом деле идёт про косинусное преобразование (частный случай, применяется в JPEG и т. д.).
И всё, что говорится про него — «разделяет сигнал на частоты». В чём заключается преобразование, что получается в результате, про оконирование — ни слова. А тут опять дьявол — в деталях. Формулы-то преобразования туда и обратно несложные, казалось бы, почему бы не выписать их? И сразу же станет видно, что результат преобразования — набор комплексных чисел и не всё там так просто.
— пишут про фильтры. Тут вообще атас, утверждения, что обрезные, шельфовые, полосовые фильтры делаются с помощью преобразования Фурье. Простой же вопрос — откуда тогда там появляется переменнй сдвиг фаз, если мы в образе были вольные его не вносить — не возникает ни у написателя статьи, ни у аудитории.
Ответ на этот вопрос очень прост: никто не реализует фильтр с помощью преобразования Фурье. Есть такие штуки — фильтры КИХ и фильтры БИХ, у каждого из них свои особенности, вот их-то все и используют. Сдвиг фаз как раз является следствием применения таких фильтров.
Куда было бы от вашей статьи больше пользы, если бы вы про Web Audio API рассказали подробнее, а не повторяли плохое изложение основ цифрового звука.
Насчёт «достаточно было написать формулу для восстановления» — совершенно не достаточно. Сколько бы человек её поняло? Для большинства это просто набор математических символов. Я специально исключил практически всю математику из статьи и даже не пытался описывать некоторые детали — это сделало бы статью в разы больше и непонятнее. Плюс к тому я вроде нигде не забыл оставить ссылки на более содержательные и подробные статьи по каждой сложной теме.
Насчёт «повторения плохого изложения» — если бы было что повторять, этой статьи вообще бы не было. Но чтобы собрать материалы у меня ушло около недели поисков по интернету и вдумчивого чтения далеко не адаптированного для обывателей материала.
Насчёт фильтров каюсь — сам не разобрался до конца в теме, перепишу этот блок. Спасибо за пояснение про то откуда берётся фазовый сдвиг.
Про Web Audio API скорее всего будет отдельная статья.
Насчёт «повторения плохого изложения» — если бы было что повторять, этой статьи вообще бы не было. Но чтобы собрать материалы у меня ушло около недели поисков по интернету и вдумчивого чтения далеко не адаптированного для обывателей материала.
Насчёт фильтров каюсь — сам не разобрался до конца в теме, перепишу этот блок. Спасибо за пояснение про то откуда берётся фазовый сдвиг.
Про Web Audio API скорее всего будет отдельная статья.
Может, я неправ, но подобных статей даже на хабре было несколько. А уж за пределами хабра…
Мне казалось, пользователи Хабра способны, видя знак бесконечности в пределе суммы понять, что нужно бесконечное число отсчётов. Конечно, всех деталей сразу не поймут, но это и не нужно — достаточно, чтобы детских заблуждений не появилось.
Про фильтры — да это не объяснение было, а так, намёк, где его искать. Для понимания лучше всего взять копию сигнала, сдвинуть на 1, 2, и т. д. сэмпла, сложить с оригиналом и посмотреть, что стало со спектром. А второй вариант — взять копию, инвертировать, прибавить и посмотреть, что стало со спектром. А можно взять три сигнала, и не просто сдвинуть и сложить, а ещё умножить часть, сдвинутую на 1 сэмпл, на 1/2, а сдвинутую на два — на -1/2.
Чтобы было легче смотреть, в качестве исходного сигнала возьмите белый шум — разница в спектре будет хорошо видна и слышна.
Сдвиг фаз? Вот он и появляется оттого, что мы сдвигаем сигнал на 1, 2,… сэмпла. Разный для разных частот потому, что сдвиг на 1 сэмпл (из 44100 Гц) на частотах 20 Гц и 20 КГц — это разный сдвиг по фазе.
В целом, вот то, что я тут описал, называется фильтр КИХ — с конечной импульсной характеристикой, он же FIR — finite impulse response. Считается просто, алгоритм реализуется в жёстком реальном времени, математически устойчив — всё хорошо, только вот копий сигнала приходится делать не три, а до нескольких тысяч. Правило простое: хотите, чтобы фильтр влиял на частоты порядка 20 Гц — вам нужно сдвигать сигнал на порядка 1/20 секунды, а при частоте дискретизации 44.1 это будет порядка 2K сэмплов. Может, потребуется в два раза больше, если хотите фильтр поточнее. Существует алгоритм построения FIR, реализующего заданную частотную характеристику с заданной точностью.
Мне казалось, пользователи Хабра способны, видя знак бесконечности в пределе суммы понять, что нужно бесконечное число отсчётов. Конечно, всех деталей сразу не поймут, но это и не нужно — достаточно, чтобы детских заблуждений не появилось.
Про фильтры — да это не объяснение было, а так, намёк, где его искать. Для понимания лучше всего взять копию сигнала, сдвинуть на 1, 2, и т. д. сэмпла, сложить с оригиналом и посмотреть, что стало со спектром. А второй вариант — взять копию, инвертировать, прибавить и посмотреть, что стало со спектром. А можно взять три сигнала, и не просто сдвинуть и сложить, а ещё умножить часть, сдвинутую на 1 сэмпл, на 1/2, а сдвинутую на два — на -1/2.
Чтобы было легче смотреть, в качестве исходного сигнала возьмите белый шум — разница в спектре будет хорошо видна и слышна.
Сдвиг фаз? Вот он и появляется оттого, что мы сдвигаем сигнал на 1, 2,… сэмпла. Разный для разных частот потому, что сдвиг на 1 сэмпл (из 44100 Гц) на частотах 20 Гц и 20 КГц — это разный сдвиг по фазе.
В целом, вот то, что я тут описал, называется фильтр КИХ — с конечной импульсной характеристикой, он же FIR — finite impulse response. Считается просто, алгоритм реализуется в жёстком реальном времени, математически устойчив — всё хорошо, только вот копий сигнала приходится делать не три, а до нескольких тысяч. Правило простое: хотите, чтобы фильтр влиял на частоты порядка 20 Гц — вам нужно сдвигать сигнал на порядка 1/20 секунды, а при частоте дискретизации 44.1 это будет порядка 2K сэмплов. Может, потребуется в два раза больше, если хотите фильтр поточнее. Существует алгоритм построения FIR, реализующего заданную частотную характеристику с заданной точностью.
Статей много, каждая о какой-то части данной статьи пишет гораздо более развёрнуто и зачастую гораздо более научным языком с кучей математики. А вот обзорной статьи, в которой бы на пальцах были объяснены основные принципы и обозначены темы для изучения я так и не нашёл. Самое близкое к этому — статья Тараса Ковриженко про нормализацию громкости.
Со знаком бесконечности как раз вопросов возникнет больше чем ответов — до этого речь идёт о каком-то конечном сигнале и тут вдруг возникает бесконечность. Откуда, почему? Если требуется бесконечное количество отсчётов, как в таком случае восстанавливать конечный сигнал? Вообще оцифровка сигнала и восстановление сигнала — это темы для двух больших отдельных статей, если не книг.
В данной конкретной реализации используется биквадратный фильтр. Он как я понял относится к фильтрам БИХ (с бесконечной импульсной характеристикой). Работает примерно также.
Берётся 2 последних отсчёта входного сигнала, 2 последних отсчёта выходного сигнала и текущий сигнал. Они умножаются на коэффициенты и складываются.
Со знаком бесконечности как раз вопросов возникнет больше чем ответов — до этого речь идёт о каком-то конечном сигнале и тут вдруг возникает бесконечность. Откуда, почему? Если требуется бесконечное количество отсчётов, как в таком случае восстанавливать конечный сигнал? Вообще оцифровка сигнала и восстановление сигнала — это темы для двух больших отдельных статей, если не книг.
В данной конкретной реализации используется биквадратный фильтр. Он как я понял относится к фильтрам БИХ (с бесконечной импульсной характеристикой). Работает примерно также.
Берётся 2 последних отсчёта входного сигнала, 2 последних отсчёта выходного сигнала и текущий сигнал. Они умножаются на коэффициенты и складываются.
С тем же успехом можно сказать, что результат преобразования Фурье — «набор действительных чисел» )
А в вебе будет 320?
Подробнее про теорему Котельникова и дискретизацию сигналов
blog.amartynov.ru/archives/%D1%82%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D0%B0-%D0%BA%D0%BE%D1%82%D0%B5%D0%BB%D1%8C%D0%BD%D0%B8%D0%BA%D0%BE%D0%B2%D0%B0-%D0%B4%D0%B8%D1%81%D0%BA%D1%80%D0%B5%D1%82%D0%B8%D0%B7%D0%B0%D1%86%D0%B8%D1%8F
blog.amartynov.ru/archives/%D1%82%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D0%B0-%D0%BA%D0%BE%D1%82%D0%B5%D0%BB%D1%8C%D0%BD%D0%B8%D0%BA%D0%BE%D0%B2%D0%B0-%D0%B4%D0%B8%D1%81%D0%BA%D1%80%D0%B5%D1%82%D0%B8%D0%B7%D0%B0%D1%86%D0%B8%D1%8F
Касательно измерения громкости:
На данный момент наиболее актуальным является стандарт измерения громкости ITU BS.1770-4 (предыдущая версия 2 используется в Европе как EBU R-128). Это полноценный стандарт, применяемый в аудио-, кино- и телеиндустрии.
Replaygain версии 1 измеряет воспринимаемую громкость, применяя фильтр обратный кривой Флетчера-Мансона и считающий RMS (вы эту аббревиатуру не упоминаете вообще и зря) 50мс отрезков аудио, плюс статистическая корректировка результата (описано упрощённо!).
Утверждение, что RG «наиболее точно передает воспринимаемый уровень громкости записи» неверно, чему является подтверждением тот факт, что в предлагаемой версии RG2 планируется использовать способ определения громкости из стандарта ITU BS.1770[1].
Часть про нормализацию полна неточностей. Нормализация — вполне конкретный термин, означающий увеличение амплитуды сигнала (т.е. повышение громкости) при которой пиковый уровень приводится к заданному значению, чаще всего к 0dBFS. Однако если говорить о нормализации громкости, то это уже комбинация алгоритмов её измерения с ограничением пиков (для предотвращения клиппинга).
Последний абзац настолько некорректен, что даже не знаю, что там комментировать.
[1] http://wiki.hydrogenaud.io/index.php?title=ReplayGain_2.0_specification
На данный момент наиболее актуальным является стандарт измерения громкости ITU BS.1770-4 (предыдущая версия 2 используется в Европе как EBU R-128). Это полноценный стандарт, применяемый в аудио-, кино- и телеиндустрии.
Replaygain версии 1 измеряет воспринимаемую громкость, применяя фильтр обратный кривой Флетчера-Мансона и считающий RMS (вы эту аббревиатуру не упоминаете вообще и зря) 50мс отрезков аудио, плюс статистическая корректировка результата (описано упрощённо!).
Утверждение, что RG «наиболее точно передает воспринимаемый уровень громкости записи» неверно, чему является подтверждением тот факт, что в предлагаемой версии RG2 планируется использовать способ определения громкости из стандарта ITU BS.1770[1].
Часть про нормализацию полна неточностей. Нормализация — вполне конкретный термин, означающий увеличение амплитуды сигнала (т.е. повышение громкости) при которой пиковый уровень приводится к заданному значению, чаще всего к 0dBFS. Однако если говорить о нормализации громкости, то это уже комбинация алгоритмов её измерения с ограничением пиков (для предотвращения клиппинга).
Последний абзац настолько некорректен, что даже не знаю, что там комментировать.
[1] http://wiki.hydrogenaud.io/index.php?title=ReplayGain_2.0_specification
о нормализации громкостиА применяется ли фильтр, аналогичный эквилизации гистограммы для изображений?
Нет, так как нормализация аудио подразумевает недеструктивное изменение сигнала.
Мне вообще не очень легко представить адекватную аналогию такого преобразования. Возможно это могло бы быть расширение динамического диапазона, но толку в этом очень мало*.
*Можно говорить о расширении динамического диапазона (декомпрессии) как о восстановительном процессе для «убитого» звука, но это обычно контролируемый вручную процесс, применяемый чаще всего на этапе мастеринга записей.
Мне вообще не очень легко представить адекватную аналогию такого преобразования. Возможно это могло бы быть расширение динамического диапазона, но толку в этом очень мало*.
*Можно говорить о расширении динамического диапазона (декомпрессии) как о восстановительном процессе для «убитого» звука, но это обычно контролируемый вручную процесс, применяемый чаще всего на этапе мастеринга записей.
А для частотного представления: автоматический эквалайзинг(приближение характеристик, например, к розовому шуму должно делать сигнал более гармоничным для восприятия)?
На ваш вопрос, на мой взгляд, нельзя ответить прямо.
1. Использование розового шума как референсного давным-давно используется звукорежиссёрами и мастеринг-инженерами. Розовый шум в данном случае используется как некий формализованный идеал, но прежде всего, как образец для корректировки восприятия звука самим звукорежиссёром. Т.е. служит средством от т.н. «замыливания слуха», когда от продолжительной работы мозг адаптируется к тому, что слышит, и выносить объективные суждения становится крайне тяжело.
2. На данный момент весьма распространены программные эквалайзеры, позволяющие переносить частотную характеристику с источника на объект обработки, однако результат их работы практически всегда если и используется, то в сглаженном виде и лишь в небольшой процентной доле. Обычно ими пользуются для сверхбыстрой оценки разницы звучания между двумя композициями и дальнейшей ручной корректировки. Подобными функциями обладают vst-плагины Fab-Filter Pro-Q2, Izotope Ozone, Melda AutoEqualizer и, вероятно, многие другие.
3. Автоматическая подгонка звучания под спектр розового шума, несомненно, возможна, но с рядом оговорок. Чтобы внести изменения в АЧХ композиции, нам для начала нужно её замерить, и здесь возникает вопрос окна замера, т.е. того временного отрезка, который будет использоваться для просчёта средней АЧХ. Если окно будет большим, то неизбежны артефакты1 (по крайней мере, при использовании средств, перечисленных во втором пункте), а если, предположим, замерять и обрабатывать очень малые кусочки исходной композиции (порядка 1-5 мс), то, как мне подсказывает интуиция, можно уничтожить всю внутреннюю пульсацию записи.
И, самое главное: не совсем ясен смысл этого действия. Музыка, в отличие от графики, раскрывается в динамике, т.е. невозможна без контрастов. Диссонансы или несбалансированное тонально звучание в одном моменте может вести к балансу и гармонизации звуков в другом, это неотъемлемая часть музыкального произведения. Так что если целью не стоит создавать «человеческую музыку» без каких-либо индивидуальных особенностей, то затея, скорее всего, бессмысленна.
[1] Предположим, обрабатывается скрипичный концерт, где в какой-то момент X вступает рояль или контрабас. Очевидно, что на полученной из замера всей записи АЧХ басовая составляющая не будет дотягивать до показателей РШ. И даже если предположить, что подгонка под его спектр улучшит звучание до точки X, после мы получим дисбаланс с перебором по низким частотам.
1. Использование розового шума как референсного давным-давно используется звукорежиссёрами и мастеринг-инженерами. Розовый шум в данном случае используется как некий формализованный идеал, но прежде всего, как образец для корректировки восприятия звука самим звукорежиссёром. Т.е. служит средством от т.н. «замыливания слуха», когда от продолжительной работы мозг адаптируется к тому, что слышит, и выносить объективные суждения становится крайне тяжело.
2. На данный момент весьма распространены программные эквалайзеры, позволяющие переносить частотную характеристику с источника на объект обработки, однако результат их работы практически всегда если и используется, то в сглаженном виде и лишь в небольшой процентной доле. Обычно ими пользуются для сверхбыстрой оценки разницы звучания между двумя композициями и дальнейшей ручной корректировки. Подобными функциями обладают vst-плагины Fab-Filter Pro-Q2, Izotope Ozone, Melda AutoEqualizer и, вероятно, многие другие.
3. Автоматическая подгонка звучания под спектр розового шума, несомненно, возможна, но с рядом оговорок. Чтобы внести изменения в АЧХ композиции, нам для начала нужно её замерить, и здесь возникает вопрос окна замера, т.е. того временного отрезка, который будет использоваться для просчёта средней АЧХ. Если окно будет большим, то неизбежны артефакты1 (по крайней мере, при использовании средств, перечисленных во втором пункте), а если, предположим, замерять и обрабатывать очень малые кусочки исходной композиции (порядка 1-5 мс), то, как мне подсказывает интуиция, можно уничтожить всю внутреннюю пульсацию записи.
И, самое главное: не совсем ясен смысл этого действия. Музыка, в отличие от графики, раскрывается в динамике, т.е. невозможна без контрастов. Диссонансы или несбалансированное тонально звучание в одном моменте может вести к балансу и гармонизации звуков в другом, это неотъемлемая часть музыкального произведения. Так что если целью не стоит создавать «человеческую музыку» без каких-либо индивидуальных особенностей, то затея, скорее всего, бессмысленна.
[1] Предположим, обрабатывается скрипичный концерт, где в какой-то момент X вступает рояль или контрабас. Очевидно, что на полученной из замера всей записи АЧХ басовая составляющая не будет дотягивать до показателей РШ. И даже если предположить, что подгонка под его спектр улучшит звучание до точки X, после мы получим дисбаланс с перебором по низким частотам.
Спасибо за ответ. Привел розовый шум в качестве примера. Вообще, мне кажется было удобно изменять степень детерминированности сигнала. Как написано в статье «A simple experiment demonstrating the connection between chaos and music»(pdf), у музыки и так распределение как у розового шума. А интересно, к примеру, подогнать под белый шум.
Диссонансы или несбалансированное тонально звучание в одном моменте может вести к балансу и гармонизации звуков в другом, это неотъемлемая часть музыкального произведения.Возможно, неотъемлемой составляющей красоты произведения является именно балансирование на грани предсказуемости и случайности.
Спасибо за названия плагинов. Ранее использовал Voxengo CurveEQ VST. iZopote использую с первой версии, не заметил как в нём тоже это появилось. Есть ли что-то подобное, но standalone, чтобы анализировало исходный и финальный трек мгновенно, без необходимости «проигрывать» его в плагин?
Обычно это используется на радио и при создании ремиксов или сетов, когда не должно быть большой разницы по EQ между разными треками.
Обычно это используется на радио и при создании ремиксов или сетов, когда не должно быть большой разницы по EQ между разными треками.
Графики опрятные, статья интересная.
Зарегистрируйтесь на Хабре, чтобы оставить комментарий
Теория звука. Что нужно знать о звуке, чтобы с ним работать. Опыт Яндекс.Музыки