Привет, Хабр!
Как законодатели мод по теме Unity на российском рынке предлагаем вам почитать интересное исследование о практическом использовании алгоритма WFC (Wave Function Collapse), построенного по образу и подобию известного принципа квантовой механики и очень удобного при процедурной генерации уровней в играх. Ранее на Хабре уже публиковался подробный рассказ об этом алгоритме. Автор сегодняшней статьи Мариан Кляйнеберг рассматривает алгоритм в контексте трехмерной графики и генерации бесконечного города. Приятного чтения!

Мы поговорим об игре, где вы идете по бесконечному городу, который процедурно генерируется по мере вашего движения. Город строится из набора блоков при помощи алгоритма WFC (коллапс волновой функции).
Играбельная сборка доступна для скачивания на сайте itch.io. Также можете взять исходный код на github. Наконец, я предлагаю видео, в котором иду по сгенерированому таким образом городу.
Я буду называть словом “ячейка” такой элемент 3D-воксельной сетки, который может содержать блок или пустовать. Словом «модуль» я буду называть блок, который может занимать такую ячейку.
Алгоритм решает, какие модули подбирать в каждую ячейку игрового мира. Массив ячеек считается волновой функцией в ненаблюдаемом виде. Таким образом, каждой ячейке соответствует множество модулей, которые могут в ней оказаться. В терминах квантовой механики можно было бы сказать, «ячейка находится в суперпозиции всех модулей». Существование мира начинается в полностью ненаблюдаемом виде, где в каждой ячейке может находиться любой модуль. Далее все ячейки схлопываются, одна за другой. Это означает, что для каждой ячейки случайным образом выбирается по одному модулю из всех возможных.
Далее следует этап распространения ограничений (constraint propagation). Для каждого модуля подбирается такое подмножество модулей, которым разрешено быть смежными с ним. Всякий раз при схлопывании модуля обновляются подмножества других модулей, которые по-прежнему допускаются в качестве смежных ему. Этап распространения ограничений – самая ресурсозатратная часть алгоритма с точки зрения вычислительной мощности.
Важный аспект алгоритма заключается в определении того, какую ячейку схлопнуть. Алгоритм всегда схлопывает ячейку с наименьшей энтропией. Это ячейка, допускающая минимальное количество вариантов выбора (то есть, ячейка с наименьшей хаотичностью). Если у всех модулей вероятность схлопывания одинакова, то наименьшая энтропия будет у той ячейки, которой соответствует минимальное количество возможных модулей. Как правило, вероятности попасть под выбор для разных наличествующих модулей отличаются. Ячейка с двумя возможными модулями, имеющими одинаковую вероятность, предусматривает более широкий выбор (большую энтропию), чем та, в которой два модуля, и для одного из них вероятность попасть под выбор очень велика, а для другого – очень мала.

(Гифка помещена ExUtumno на Github)
Более подробную информацию об алгоритме коллапса волновой функции, а также ряд красивых примеров можно посмотреть здесь. Изначально этот алгоритм был предложен для генерации 2D-текстур на основе единственного образца. В таком случае вероятностные показатели модулей и правила смежности определяются в зависимости от их встречаемости в примере. В данной статье эта информация предоставляется вручную.
Вот видео, демонстрирующее этот алгоритм в действии.
Мир генерируется из набора, в котором около 100 блоков. Я создал их при помощи Blender. Сначала блоков у меня было совсем немного, и я понемногу добавлял их, когда считал это нужным.

Алгоритму необходимо знать, какие модули могут располагаться рядом друг с другом. Для каждого модуля существует 6 списков возможных соседей, по одному в каждом из направлений. Однако, я хотел избежать необходимости создавать такой список вручную. Кроме того, я хотел автоматически генерировать повернутые варианты для каждого из моих блоков.
Обе эти задачи решаемы при помощи так называемых прототипов модулей. В сущности, это
Сложная проблема возникла с моделированием информации о смежности, так, чтобы этот автоматический процесс работал. Вот что у меня получилось:

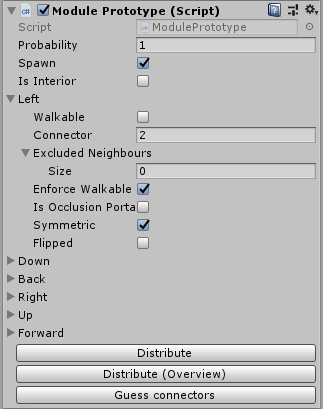
У каждого блока по 6 контактов, по одному на каждую грань. У контакта есть номер. Кроме того, горизонтальные контакты могут быть перевернуты, неперевернуты или симметричны. Вертикальные контакты либо имеют индекс вращения в диапазоне от 0 до 3, либо помечаются как вращательно инвариантные.
Исходя из этого, я могу автоматически проверять, каким модулям разрешено прилегать друг к другу. У смежных модулей должны быть одинаковые номера контактов. Также должна совпадать их симметрия (одинаковый индекс вращения по вертикали, пара из перевернутого и непервернутого контакта по горизонтали), либо модули должны быть симметричны/инвариантны.
Существуют правила исключения, при помощи которых я могу запрещать варианты соседства, которые по умолчанию были бы разрешены. Некоторые блоки с подходящими друг к другу контактами попросту некрасиво выглядят рядом. Вот пример карты, сгенерированной без применения правил исключения:

Исходные алгоритм коллапса волновой функции генерирует карты конечного размера. Я же хотел построить мир, который будет все расширяться и расширяться по мере того, как вы по нему двигаетесь.
Сначала я попробовал генерировать фрагменты конечного размера и пользоваться контактами смежных фрагментов как ограничениями. Если фрагмент сгенерирован, а смежный ему фрагмент также сгенерирован, то допускаются лишь такие модули, которые укладываются рядом с имеющимися модулями. С данным подходом возникает такая проблема: всякий раз при схлопывании ячейки распространение ограничений будет урезать возможности даже на расстоянии в несколько ячеек. На следующем изображении заметны последствия схлопывания единственной ячейки:

Если на каждом шаге алгоритма генерировать всего один фрагмент, то ограничения не распространяются на смежные с ним фрагменты. В таком случае внутри фрагмента выбирались такие модули, которые оказались бы недопустимы, если принимать во внимание другие фрагменты. В результате, когда алгоритм пытался сгенерировать следующий фрагмент, он мог не найти ни одного решения.
Теперь я уже не использую фрагменты, а храню карту в словаре, отображающем позицию ячейки на ячейку. Ячейка заполняется, только если это необходимо. Некоторые элементы алгоритма следует откорректировать с учетом этого момента. При выборе ячейки, которая должна схлопнуться, невозможно учесть все ячейки, если количество их бесконечно. Вместо этого мы единовременно генерируем лишь небольшой участок карты, как только игрок его достигнет. Вне этой области продолжают распространяться ограничения.
В некоторых случаях данный подход не работает. Рассмотрим набор модулей для прямолинейного участка туннеля с показанного выше рисунка – входа в туннель там нет. Если алгоритм выберет такой туннельный модуль, то туннель по определению получится бесконечным. На этапе распространения ограничений программа попытается выделить бесконечное количество ячеек. Я разработал специальный набор модулей, чтобы обойти эту проблему.
Здесь существуют два важных граничных условия. Все грани на верхнем уровне карты должны иметь «воздушные» контакты. Все грани на основании карты должны иметь «твердые» контакты. Если эти условия не выполняются, то на карте будут лунки в земле, а некоторые здания окажутся без крыши.
На карте конечного размера эта задача решалась бы легко. Для всех ячеек на самом верхнем и самом нижнем уровне потребовалось бы удалить все модули с неподходящими контактами. Затем запустить распространение ограничений и удалить остальные модули, которые нам больше не подходят.
На карте бесконечного размера подобное не сработает, поскольку как на самом верхнем, так и на самом нижнем уровне у нас бесконечное количество ячеек. Наиболее наивное решение – удалять все неподходящие ячейки сразу по мере их возникновения. Однако, при удалении модуля на верхнем уровне срабатывают ограничения, касающиеся тех ячеек, что к нему прилегали. Возникает лавинообразный эффект, вновь приводящий к бесконечному выделению ячеек.
Я решил эту проблему, создав карту размером 1×n×1, где n — высота. Данная карта использует закольцовывание мира (world wrapping) для распространения ограничений. Механизм работает как в игре Pacman: выходя за правый край карты, персонаж возвращается на нее из-за левого края. Теперь я могу применять на моей карте распространение любых ограничений. Всякий раз при создании новой ячейки на бесконечной карте, эта ячейка инициализируется с набором модулей, соответствующим конкретной позиции на карте.
Иногда алгоритм WFC достигает такого состояния, в котором ячейке не соответствует ни одного возможного модуля. В приложениях, где мы имеем дело с миром конечного размера, можно попросту сбросить результат и начать все сначала. В бесконечном мире это не сработает, так как часть мира уже показана игроку. Сначала я остановился на решении, в котором места возникновения ошибок заполнялись белыми блоками.
В настоящее время я использую поиск с возвратом. Порядок схлопывания ячеек и некоторая информация о распространении ограничений хранится в виде истории. Если алгоритм WFC отказывает, то часть истории отменяется. Как правило, это работает, но иногда ошибки удается распознать слишком поздно, и поиск с возвратом охватывает очень много шагов. В редких случаях та ячейка, в которой находится игрок, регенерируется.
На мой взгляд, из-за такого ограничения применение алгоритма WFC с бесконечными мирами не подходит для коммерческих игр.
Я взялся за проработку этой задачи после того, как посмотрел лекцию Оскара Стельберга, рассказывающего, как он использует алгоритм для генерации уровней в игре Bad North. В общих чертах мой алгоритм был реализован во время недели procjam.
У меня есть некоторые идеи о дальнейшей доработке этого алгоритма, но я не уверен, что когда-нибудь соберусь добавить к нему геймплей. А если и соберусь – наверняка это будет не такая эпичная стратегия, которую вы себе уже вообразили. Однако, если вы хотите проверить, как работает с этим алгоритмом ваша любимая игровая механика – просто попробуйте сами! В конце концов, исходный код выложен в открытом доступе и лицензирован MIT.
Как законодатели мод по теме Unity на российском рынке предлагаем вам почитать интересное исследование о практическом использовании алгоритма WFC (Wave Function Collapse), построенного по образу и подобию известного принципа квантовой механики и очень удобного при процедурной генерации уровней в играх. Ранее на Хабре уже публиковался подробный рассказ об этом алгоритме. Автор сегодняшней статьи Мариан Кляйнеберг рассматривает алгоритм в контексте трехмерной графики и генерации бесконечного города. Приятного чтения!

Мы поговорим об игре, где вы идете по бесконечному городу, который процедурно генерируется по мере вашего движения. Город строится из набора блоков при помощи алгоритма WFC (коллапс волновой функции).
Играбельная сборка доступна для скачивания на сайте itch.io. Также можете взять исходный код на github. Наконец, я предлагаю видео, в котором иду по сгенерированому таким образом городу.
Алгоритм
Я буду называть словом “ячейка” такой элемент 3D-воксельной сетки, который может содержать блок или пустовать. Словом «модуль» я буду называть блок, который может занимать такую ячейку.
Алгоритм решает, какие модули подбирать в каждую ячейку игрового мира. Массив ячеек считается волновой функцией в ненаблюдаемом виде. Таким образом, каждой ячейке соответствует множество модулей, которые могут в ней оказаться. В терминах квантовой механики можно было бы сказать, «ячейка находится в суперпозиции всех модулей». Существование мира начинается в полностью ненаблюдаемом виде, где в каждой ячейке может находиться любой модуль. Далее все ячейки схлопываются, одна за другой. Это означает, что для каждой ячейки случайным образом выбирается по одному модулю из всех возможных.
Далее следует этап распространения ограничений (constraint propagation). Для каждого модуля подбирается такое подмножество модулей, которым разрешено быть смежными с ним. Всякий раз при схлопывании модуля обновляются подмножества других модулей, которые по-прежнему допускаются в качестве смежных ему. Этап распространения ограничений – самая ресурсозатратная часть алгоритма с точки зрения вычислительной мощности.
Важный аспект алгоритма заключается в определении того, какую ячейку схлопнуть. Алгоритм всегда схлопывает ячейку с наименьшей энтропией. Это ячейка, допускающая минимальное количество вариантов выбора (то есть, ячейка с наименьшей хаотичностью). Если у всех модулей вероятность схлопывания одинакова, то наименьшая энтропия будет у той ячейки, которой соответствует минимальное количество возможных модулей. Как правило, вероятности попасть под выбор для разных наличествующих модулей отличаются. Ячейка с двумя возможными модулями, имеющими одинаковую вероятность, предусматривает более широкий выбор (большую энтропию), чем та, в которой два модуля, и для одного из них вероятность попасть под выбор очень велика, а для другого – очень мала.

(Гифка помещена ExUtumno на Github)
Более подробную информацию об алгоритме коллапса волновой функции, а также ряд красивых примеров можно посмотреть здесь. Изначально этот алгоритм был предложен для генерации 2D-текстур на основе единственного образца. В таком случае вероятностные показатели модулей и правила смежности определяются в зависимости от их встречаемости в примере. В данной статье эта информация предоставляется вручную.
Вот видео, демонстрирующее этот алгоритм в действии.
О блоках, прототипах и модулях
Мир генерируется из набора, в котором около 100 блоков. Я создал их при помощи Blender. Сначала блоков у меня было совсем немного, и я понемногу добавлял их, когда считал это нужным.

Алгоритму необходимо знать, какие модули могут располагаться рядом друг с другом. Для каждого модуля существует 6 списков возможных соседей, по одному в каждом из направлений. Однако, я хотел избежать необходимости создавать такой список вручную. Кроме того, я хотел автоматически генерировать повернутые варианты для каждого из моих блоков.
Обе эти задачи решаемы при помощи так называемых прототипов модулей. В сущности, это
MonoBehaviour, с которым удобно работать в редакторе Unity. Модули вместе со списками допустимых соседних элементов и повернутыми вариантами автоматически создаются на основе таких прототипов.Сложная проблема возникла с моделированием информации о смежности, так, чтобы этот автоматический процесс работал. Вот что у меня получилось:

У каждого блока по 6 контактов, по одному на каждую грань. У контакта есть номер. Кроме того, горизонтальные контакты могут быть перевернуты, неперевернуты или симметричны. Вертикальные контакты либо имеют индекс вращения в диапазоне от 0 до 3, либо помечаются как вращательно инвариантные.
Исходя из этого, я могу автоматически проверять, каким модулям разрешено прилегать друг к другу. У смежных модулей должны быть одинаковые номера контактов. Также должна совпадать их симметрия (одинаковый индекс вращения по вертикали, пара из перевернутого и непервернутого контакта по горизонтали), либо модули должны быть симметричны/инвариантны.

Существуют правила исключения, при помощи которых я могу запрещать варианты соседства, которые по умолчанию были бы разрешены. Некоторые блоки с подходящими друг к другу контактами попросту некрасиво выглядят рядом. Вот пример карты, сгенерированной без применения правил исключения:

Путь к бесконечности
Исходные алгоритм коллапса волновой функции генерирует карты конечного размера. Я же хотел построить мир, который будет все расширяться и расширяться по мере того, как вы по нему двигаетесь.
Сначала я попробовал генерировать фрагменты конечного размера и пользоваться контактами смежных фрагментов как ограничениями. Если фрагмент сгенерирован, а смежный ему фрагмент также сгенерирован, то допускаются лишь такие модули, которые укладываются рядом с имеющимися модулями. С данным подходом возникает такая проблема: всякий раз при схлопывании ячейки распространение ограничений будет урезать возможности даже на расстоянии в несколько ячеек. На следующем изображении заметны последствия схлопывания единственной ячейки:

Если на каждом шаге алгоритма генерировать всего один фрагмент, то ограничения не распространяются на смежные с ним фрагменты. В таком случае внутри фрагмента выбирались такие модули, которые оказались бы недопустимы, если принимать во внимание другие фрагменты. В результате, когда алгоритм пытался сгенерировать следующий фрагмент, он мог не найти ни одного решения.
Теперь я уже не использую фрагменты, а храню карту в словаре, отображающем позицию ячейки на ячейку. Ячейка заполняется, только если это необходимо. Некоторые элементы алгоритма следует откорректировать с учетом этого момента. При выборе ячейки, которая должна схлопнуться, невозможно учесть все ячейки, если количество их бесконечно. Вместо этого мы единовременно генерируем лишь небольшой участок карты, как только игрок его достигнет. Вне этой области продолжают распространяться ограничения.
В некоторых случаях данный подход не работает. Рассмотрим набор модулей для прямолинейного участка туннеля с показанного выше рисунка – входа в туннель там нет. Если алгоритм выберет такой туннельный модуль, то туннель по определению получится бесконечным. На этапе распространения ограничений программа попытается выделить бесконечное количество ячеек. Я разработал специальный набор модулей, чтобы обойти эту проблему.
Граничные условия
Здесь существуют два важных граничных условия. Все грани на верхнем уровне карты должны иметь «воздушные» контакты. Все грани на основании карты должны иметь «твердые» контакты. Если эти условия не выполняются, то на карте будут лунки в земле, а некоторые здания окажутся без крыши.
На карте конечного размера эта задача решалась бы легко. Для всех ячеек на самом верхнем и самом нижнем уровне потребовалось бы удалить все модули с неподходящими контактами. Затем запустить распространение ограничений и удалить остальные модули, которые нам больше не подходят.
На карте бесконечного размера подобное не сработает, поскольку как на самом верхнем, так и на самом нижнем уровне у нас бесконечное количество ячеек. Наиболее наивное решение – удалять все неподходящие ячейки сразу по мере их возникновения. Однако, при удалении модуля на верхнем уровне срабатывают ограничения, касающиеся тех ячеек, что к нему прилегали. Возникает лавинообразный эффект, вновь приводящий к бесконечному выделению ячеек.
Я решил эту проблему, создав карту размером 1×n×1, где n — высота. Данная карта использует закольцовывание мира (world wrapping) для распространения ограничений. Механизм работает как в игре Pacman: выходя за правый край карты, персонаж возвращается на нее из-за левого края. Теперь я могу применять на моей карте распространение любых ограничений. Всякий раз при создании новой ячейки на бесконечной карте, эта ячейка инициализируется с набором модулей, соответствующим конкретной позиции на карте.
Состояния ошибок и поиск с возвратом
Иногда алгоритм WFC достигает такого состояния, в котором ячейке не соответствует ни одного возможного модуля. В приложениях, где мы имеем дело с миром конечного размера, можно попросту сбросить результат и начать все сначала. В бесконечном мире это не сработает, так как часть мира уже показана игроку. Сначала я остановился на решении, в котором места возникновения ошибок заполнялись белыми блоками.
В настоящее время я использую поиск с возвратом. Порядок схлопывания ячеек и некоторая информация о распространении ограничений хранится в виде истории. Если алгоритм WFC отказывает, то часть истории отменяется. Как правило, это работает, но иногда ошибки удается распознать слишком поздно, и поиск с возвратом охватывает очень много шагов. В редких случаях та ячейка, в которой находится игрок, регенерируется.
На мой взгляд, из-за такого ограничения применение алгоритма WFC с бесконечными мирами не подходит для коммерческих игр.
Предыстория
Я взялся за проработку этой задачи после того, как посмотрел лекцию Оскара Стельберга, рассказывающего, как он использует алгоритм для генерации уровней в игре Bad North. В общих чертах мой алгоритм был реализован во время недели procjam.
У меня есть некоторые идеи о дальнейшей доработке этого алгоритма, но я не уверен, что когда-нибудь соберусь добавить к нему геймплей. А если и соберусь – наверняка это будет не такая эпичная стратегия, которую вы себе уже вообразили. Однако, если вы хотите проверить, как работает с этим алгоритмом ваша любимая игровая механика – просто попробуйте сами! В конце концов, исходный код выложен в открытом доступе и лицензирован MIT.