 Привет, Хаброжители! Алгоритмы — это сердце и душа computer science. Без них не обойтись, они есть везде — от сетевой маршрутизации и расчетов по геномике до криптографии и машинного обучения. «Совершенный алгоритм» превратит вас в настоящего профи, который будет ставить задачи и мастерски их решать как в жизни, так и на собеседовании при приеме на работу в любую IT-компанию.
Привет, Хаброжители! Алгоритмы — это сердце и душа computer science. Без них не обойтись, они есть везде — от сетевой маршрутизации и расчетов по геномике до криптографии и машинного обучения. «Совершенный алгоритм» превратит вас в настоящего профи, который будет ставить задачи и мастерски их решать как в жизни, так и на собеседовании при приеме на работу в любую IT-компанию. Если вы уже достаточно прокачались в асимптотическом анализе, жадных алгоритмах и динамическом программировании, самое время рассмотреть понятие NP-трудности, которое часто вызывает неподдельный страх. Тим Рафгарден покажет, как распознать NP-трудную задачу, расскажет, как избежать решения с нуля, и поможет найти эффективные пути решения.
От автора
Перед вами четвертая из серии книг, написанных на базе проводимых мною с 2012 года онлайн-курсов по алгоритмам. Эти курсы, в свою очередь, появились благодаря лекциям для студентов, которые я читал в Стэнфордском университете в течение многих лет. Четвертая часть исходит из того, что читатель уже немного знаком с асимптотическим анализом и О-большим, поиском в графах и алгоритмами кратчайшего пути, жадными алгоритмами и динамическим программированием (все эти темы освещены в предыдущих частях).
О чем эти книги
Четвертая часть серии «Совершенный алгоритм» посвящена NP-трудным задачам и работе с ними.
Алгоритмические инструменты для решения NP-трудных задач. Многие реальные задачи являются NP-трудными и кажутся не поддающимися решению теми типами всегда правильных и всегда быстрых алгоритмов, которые были представлены в предыдущих частях. При встрече с NP-трудной задачей придется пойти на компромисс между правильностью и скоростью. Вы увидите старые методы (жадные алгоритмы) и новые (локальный поиск) для разработки быстрых «приближенно правильных» эвристических алгоритмов для работы с приложениями по задачам планирования, максимизации влияния в социальных сетях и задаче коммивояжера. Мы также рассмотрим старые методы (динамическое программирование) и новые (решатели задач смешанного целочисленного программирования и задач выполнимости булевых формул) для улучшения работы алгоритмов исчерпывающего поиска. Приложения будут включать задачу коммивояжера, поиск сигнальных путей в биологических сетях и переупаковку телевизионных станций на аукционе радиочастотного спектра в США.
Распознавание NP-трудных задач. Эта книга научит вас быстро распознавать NP-трудную задачу и не тратить время на разработку идеального алгоритма для ее решения. Вы познакомитесь с многочисленными широко известными и базовыми NP-трудными задачами, начиная от задач выполнимости и раскраски графов и заканчивая задачей о гамильтоновом пути. Вы попробуете доказать NP-трудность с помощью редукций.
Для более подробного ознакомления с содержанием книги загляните в разделы «Выводы», где выделены наиболее важные моменты. «Полевое руководство по разработке алгоритмов» на с. 283 даст представление о том, как темы этой книги вписываются в общую алгоритмическую картину.
Разделы книги, помеченные звездочками, — самые продвинутые. Читатели, испытывающие нехватку времени, могут пропустить их при первом чтении без потери непрерывности.
Темы, затронутые в первых трех частях.Первая часть серии «Совершенный алгоритм» охватывает асимптотические обозначения (О-большое и его близких родственников), алгоритмы «разделяй и властвуй» и основной метод, рандомизированные алгоритмы, быструю сортировку и ее анализ, а также линейно-временные алгоритмы отбора. Во второй части рассмотрены различные структуры данных (кучи, сбалансированные деревья поиска, хеш-таблицы, фильтры Блума), графовые примитивы (поиск сначала в ширину и сначала в глубину, связность, кратчайшие пути) и области их применения (от дедупликации до анализа социальных сетей). Третья часть посвящена жадным алгоритмам (задаче планирования, определению минимального остовного дерева графа, кластеризации, кодам Хаффмана), а также динамическому программированию (задаче о рюкзаке, выравниванию рядов, поиску кратчайших путей, построению деревьев оптимального поиска).
Навыки, которые вы приобретете
Освоение алгоритмов требует времени и усилий. Ради чего все это?
Возможность стать более эффективным программистом. Вы изучите несколько невероятно быстрых подпрограмм для обработки данных и несколько полезных структур для организации данных, которые можете применять непосредственно в ваших собственных программах. Реализация и применение этих алгоритмов расширят и улучшат ваши навыки программирования. Вы также узнаете основные приемы разработки алгоритмов, которые актуальны для решения разнообразных задач в широких областях, получите инструменты для прогнозирования производительности этих алгоритмов. Такие шаблоны могут быть вам полезны для разработки новых алгоритмов решения задач, которые возникают в вашей собственной работе.
Развитие аналитических способностей. Алгоритмические описания, мыслительная работа над алгоритмами дают большой опыт. Посредством математического анализа вы получите углубленное понимание конкретных алгоритмов и структур данных, описанных в этой книге. Вы приобретете навыки работы с несколькими математическими методами, которые широко применяются для анализа алгоритмов.
Алгоритмическое мышление. Научившись разбираться в алгоритмах, трудно не заметить, что они окружают нас повсюду, едете ли вы в лифте, наблюдаете ли за стаей птиц, управляете ли вы своим инвестиционным портфелем или даже наблюдаете за тем, как учится ребенок. Алгоритмическое мышление становится все более полезным и распространенным в дисциплинах, не связанных с информатикой, включая биологию, статистику и экономику.
Знакомство с величайшими достижениями информатики. Изучение алгоритмов напоминает просмотр эффектного клипа с многочисленными суперхитами минувших шестидесяти лет развития информатики. Вы больше не будете чувствовать себя чужим на фуршете для специалистов в области computer science, когда кто-то отпустит шутку по поводу алгоритма Дейкстры. Прочитав эти книги, вы будете точно знать, что он имеет в виду.
Успешность при прохождении собеседования. На протяжении многих лет бесчисленные студенты развлекали меня рассказами о том, как знания, почерпнутые из этих книг, позволяли им успешно справляться с любым техническим вопросом, который им задавали во время собеседования.
Возможность стать более эффективным программистом. Вы изучите несколько невероятно быстрых подпрограмм для обработки данных и несколько полезных структур для организации данных, которые можете применять непосредственно в ваших собственных программах. Реализация и применение этих алгоритмов расширят и улучшат ваши навыки программирования. Вы также узнаете основные приемы разработки алгоритмов, которые актуальны для решения разнообразных задач в широких областях, получите инструменты для прогнозирования производительности этих алгоритмов. Такие шаблоны могут быть вам полезны для разработки новых алгоритмов решения задач, которые возникают в вашей собственной работе.
Развитие аналитических способностей. Алгоритмические описания, мыслительная работа над алгоритмами дают большой опыт. Посредством математического анализа вы получите углубленное понимание конкретных алгоритмов и структур данных, описанных в этой книге. Вы приобретете навыки работы с несколькими математическими методами, которые широко применяются для анализа алгоритмов.
Алгоритмическое мышление. Научившись разбираться в алгоритмах, трудно не заметить, что они окружают нас повсюду, едете ли вы в лифте, наблюдаете ли за стаей птиц, управляете ли вы своим инвестиционным портфелем или даже наблюдаете за тем, как учится ребенок. Алгоритмическое мышление становится все более полезным и распространенным в дисциплинах, не связанных с информатикой, включая биологию, статистику и экономику.
Знакомство с величайшими достижениями информатики. Изучение алгоритмов напоминает просмотр эффектного клипа с многочисленными суперхитами минувших шестидесяти лет развития информатики. Вы больше не будете чувствовать себя чужим на фуршете для специалистов в области computer science, когда кто-то отпустит шутку по поводу алгоритма Дейкстры. Прочитав эти книги, вы будете точно знать, что он имеет в виду.
Успешность при прохождении собеседования. На протяжении многих лет бесчисленные студенты развлекали меня рассказами о том, как знания, почерпнутые из этих книг, позволяли им успешно справляться с любым техническим вопросом, который им задавали во время собеседования.
В чем особенность этой книги
Эта книга предназначена только для одного: постараться научить основам алгоритмизации максимально доступным способом. Воспринимайте ее как конспект лекций, которые опытный наставник по алгоритмам будет давать вам на протяжении серии индивидуальных уроков.
Существует ряд прекрасных, гораздо более традиционных и энциклопедически выверенных учебников по алгоритмам. Любой из них с пользой украсит эту серию книг дополнительными деталями, задачами и темами. Хотелось бы, чтобы вы поискали и нашли что-то полезное среди этих книг для себя. Кроме того, есть книги, которые ориентируются на программистов, ищущих готовые реализации алгоритмов на конкретном языке программирования. Множество соответствующих примеров также находятся в свободном доступе в интернете.
19.2. Возможные уровни профессиональной компетенции
Одни вычислительные задачи проще, чем другие. Суть теории NP-трудности состоит в классификации задач — выделении легкорешаемых (подобных задаче о минимальном остовном дереве) и труднорешаемых (подобных задаче коммивояжера). Эта книга нацелена как на читателей, ищущих пособие начального уровня по этой теме, так и на тех, кто стремится к компетенции профессионального уровня. В этом разделе даются рекомендации, как подойти к остальной части книги в зависимости от ваших целей и ограничений.
Каковы ваши текущие и желаемые уровни профессиональной компетенции в распознавании и решении NP-трудных задач?
Уровень 0: «Что такое NP-трудная задача?»
Это полное невежество — вы никогда не слышали об NP-трудности и не знаете, что многие практически релевантные вычислительные задачи считаются не поддающимися решению быстрым алгоритмом. Если я все сделал правильно, то эта книга будет доступной даже читателям уровня 0.
Уровень 1: «О, задача-то NP-трудная? Думаю, что мы должны либо переформулировать задачу (снизить поставленные нами цели), либо вложить больше ресурсов в ее решение».
Это осведомленность на уровне коктейльной вечеринки и, по меньшей мере, владение слухами об NP-трудности. Например, управляя своим софтверным проектом, используете ли вы алгоритмическую либо оптимизационную компоненты? Если да, то вам следует приобрести знания уровня 1 на случай, если один из членов вашей команды столкнется с NP-трудной задачей и захочет обсудить с вами возможные дальнейшие шаги. Для этого изучите разделы 19.3, 19.4 и 19.6.
Уровень 2: «О, задача-то NP-трудная? Дайте мне шанс применить мой алгоритмический опыт и посмотрим, насколько далеко я смогу зайти».
Разработчики ПО при достижении уровня 2 приобретают уверенность и богатый инструментарий для разработки практически полезных алгоритмов решения или аппроксимации NP-трудных задач. Серьезные программисты должны быть нацелены на этот уровень (или выше). К счастью, все алгоритмические парадигмы, которые мы развернули в предыдущих частях серии, также полезны для продвижения к NP-трудным задачам. Главы 20 и 21 приведут вас к уровню 2, в разделе 19.4 вы найдете обзор, а в главе 24 — исследование инструментария уровня 2 и его применение.
Уровень 3: «Расскажите поподробнее о задаче. [...внимательно слушает.. .] Мои соболезнования, она — NP-трудная».
Вы можете быстро распознавать NP-трудность: знаете несколько известных NP-трудных задач и можете доказать NP-трудность дополнительных задач. Эти навыки позволяют вам консультировать по алгоритмическим вопросам коллег, студентов или инженеров в промышленности. Глава 22 содержит курс молодого бойца для повышения вашего уровня до 3, а раздел 19.5 — обзор.
Уровень 4: «Давайте я вам объясню вот тут на доске предположение, что P ≠ NP».
Самый продвинутый уровень предназначен для начинающих теоретиков и тех, кто ищет строгого математического понимания NP-трудности и рассмотрения вопроса «P против NP». Если этот уровень вас не отпугивает, прочтите дополнительную главу 23.
19.3. «Легкие» и «трудные» задачи
Противопоставление «легкой» и «трудной» задач в теории NP-трудности простыми словами звучит так:
«легкая» может быть решена полиномиально-временным алгоритмом,
«трудная» в худшем случае требует экспоненциального времени.
Это краткое изложение NP-трудности упускает из виду несколько важных тонкостей (см. раздел 19.3.9). Но если через десять лет о смысле NP-трудности вы вспомните только эти несколько слов, то они будут самыми точными.
19.3.1. Полиномиально-временные алгоритмы
Чтобы перейти к определению «легкой» задачи, давайте вспомним время выполнения некоторых известных алгоритмов (из предыдущих частей серии):
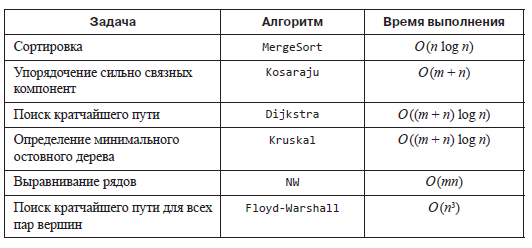
Точный смысл n и m зависит от конкретной задачи, но во всех случаях они связаны с размером входных данных. Согласно таблице, хотя время выполнения алгоритмов варьируется, все они зависят от размера входных данных в рамках полиномиальной функции. В общем случае:
Полиномиально-временные алгоритмы
Полиномиально-временной алгоритм — это алгоритм с временем выполнения, в наихудшем случае равным, где n обозначает размер входных данных и d — это константа (независимая от n).
Все шесть алгоритмов являются полиномиально-временными (с достаточно малыми экспонентами d). Все ли естественные алгоритмы выполняются за полиномиальное время? Нет. Например, для многих задач исчерпывающий поиск выполняется за время, экспоненциально зависящее от размера входных данных (как указано во второй сноске к задаче о минимальном остовном дереве). В полиномиально-временных алгоритмах, которые мы ранее изучили, есть кое-что особенное.
19.3.2. Полиномиальное время против экспоненциального
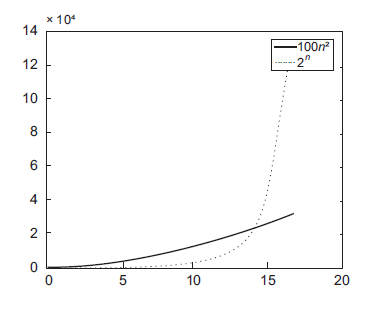
Не забывайте, что любая экспоненциальная функция в конечном счете растет намного быстрее любой полиномиальной функции. Между типичным полиномиальным и экспоненциальным временем выполнения существует огромная разница, даже для очень малых экземпляров. Рассмотрите график, на котором изображены полиномиальная функция 100n^2 и экспоненциальная функция 2^n.
Закон Мура утверждает, что вычислительная мощность, доступная по данной цене, удваивается каждые 1–2 года. Означает ли это, что разница между полиномиально- и экспоненциально-временными алгоритмами со временем исчезнет? На самом деле наоборот! Вычислительные амбиции растут вместе с вычислительной мощностью, и с течением времени мы видим все более крупные размеры входных данных и страдаем от все более огромной пропасти между полиномиальным и экспоненциальным периодами выполнения.
Представьте фиксированный бюджет времени, например час или день. Как масштабируется поддающийся решению размер входных данных вместе с добавочной вычислительной мощностью? С полиномиально-временным алгоритмом он увеличивается на постоянный коэффициент (например, с 1 000 000 до 1 414 213) с каждым удвоением вычислительной мощности.14 С алгоритмом, который работает со временем, пропорциональным 2^n, где n — это размер входных данных, каждое удвоение вычислительной мощности увеличивает поддающийся решению размер входных данных только на единицу (например, с 1 000 000 до 1 000 001)!
19.3.3. Легкорешаемые задачи
Теория NP-трудности определяет, что «легкие» задачи поддаются решению полиномиально-временным алгоритмом или, что эквивалентно, алгоритмом, для которого поддающийся решению размер входных данных (для фиксированного бюджета времени) масштабируется мультипликативно вместе с увеличением вычислительной мощности:
Задачи, поддающиеся решению за полиномиальное время
Вычислительная задача поддается решению за полиномиальное время, если существует полиномиально-временной алгоритм, который решает ее правильно для каждого элемента входных данных.
Например, все шесть перечисленных задач поддаются решению за полиномиальное время.
Технически алгоритм (бесполезный на практике), который выполняется за время
Технически алгоритм (бесполезный на практике), который выполняется за время O (n^100) на n-размерных входных данных, считается полиномиально-временным, и задача, решенная таким алгоритмом, квалифицируется как поддающаяся решению за полиномиальное время. Если перевернуть это утверждение, окажется, что если задача, такая как задача коммивояжера, не поддается решению за полиномиальное время, то не существует даже O (n^100)-временного или O (n^10 000)-временного алгоритма, который ее решит (!).
Смелость, определения и крайние случаи
Отождествление понятия «легкая» с понятием «поддающаяся решению за полиномиальное время» страдает несовершенством. Задача может быть решена в теории (с помощью алгоритма, который технически выполняется за полиномиальное время), но не в реальности (посредством эмпирически быстрого алгоритма), или наоборот. Любой, у кого хватит смелости написать точное математическое определение (например, полиномиально-временной решаемости), чтобы выразить беспорядочную концепцию реального мира (например, «легко решить посредством компьютера в физическом мире»), должен быть готов к трениям между двоичной природой определения и нечеткостью реальности. Определение неизбежно будет включать или исключать некоторые крайние случаи, которые хочется обойти, но это не повод игнорировать или отклонять хорошее определение. Полиномиально-временная решаемость эффективна в разделении задач на «легкие» и «трудные» на эмпирической основе. Имея за плечами полвека свидетельств, мы можем с уверенностью сказать, что естественные задачи, поддающиеся решению за полиномиальное время, в типичной ситуации могут решаться практическими общецелевыми алгоритмами и что задачи, считающиеся не поддающимися решению за полиномиальное время, в типичной ситуации требуют значительно больше работы и компетенции в предметной области.
19.3.4. Относительная труднорешаемость
Предположим, вы заподозрили, что задача, такая как задача коммивояжера, «не является легкой», имея в виду, что она не поддается решению любым полиномиально-временным алгоритмом (независимо от того, насколько крупным является полином). Как это доказать? Самым убедительным аргументом, конечно, будет герметичное математическое доказательство. Но статус задачи коммивояжера остается в подвешенном состоянии: никто не нашел полиномиально-временного алгоритма, который ее решает, или доказательства, что такого алгоритма не существует.
Как развить теорию, которая с пользой дифференцирует «легкие» и «трудные» задачи при нашем недостаточном понимании всех возможностей алгоритмов? Блестящая идея теории NP-трудности состоит в классификации задач на основе их относительной (а не абсолютной) трудности и объявления задачи «трудной», если она «по меньшей мере так же трудна, как» подавляющее число других нерешенных задач.
19.3.5. Трудные задачи
Безуспешные попытки решить задачу коммивояжера (раздел 19.1.3) дают косвенные свидетельства, что эта задача, возможно, не решается за полиномиальное время.
Слабые доказательства трудности
Полиномиально-временной алгоритм решил бы задачу коммивояжера, которая сопротивлялась усилиям сотен (если не тысяч) умов на протяжении десятилетий.
Есть ли более убедительный аргумент? Основная идея NP-трудности состоит в том, чтобы показать, что такая задача, как задача коммивояжера, по меньшей мере так же трудна, как и огромное количество нерешенных задач из множества различных научных областей. По сути, в этих задачах легко распознаются решения, стоит только вам понять задачу. А значит, гипотетический полиномиально-временной алгоритм для задачи коммивояжера автоматически будет решать и остальные нерешенные задачи!
Сильные доказательства трудности
Полиномиально-временной алгоритм для задачи коммивояжера позволил бы решить тысячи задач, которые на протяжении десятилетий противостояли усилиям десятков (если не сотен)тысяч умов.
В сущности, теория NP-трудности показывает, что тысячи вычислительных задач являются замаскированными вариантами одной и той же задачи, и полиномиально-временной алгоритм для одной из NP-трудных задач решит все остальные.
Мы называем задачу NP-трудной, если есть веские свидетельства труднорешаемости в указанном выше смысле:
NP-трудность (главная идея)
Задача является NP-трудной, если она по меньшей мере так же трудна, как и любая задача, решения которой вы легко распознáете, если поймете ее суть.
Эта идея будет полностью подтверждена в разделе 23.3.4. А пока мы поработаем с предварительным определением NP-трудности в терминах широко известного математического предположения, что P ≠ NP.
19.3.6. Предположение, что P ≠ NP
Возможно, вы слышали о предположении, что P ≠ NP. Что оно собой представляет? Раздел 23.4 содержит его точную математическую формулировку, но на данный момент мы остановимся на неформальной версии, которая звучит как девиз при проверке домашнего задания:
Предположение, что P ≠ NP (неформальная версия)
Проверить предполагаемое решение задачи точно проще, чем создать собственное решение с нуля.
Здесь P и NP относятся соответственно к задачам, которые могут быть решены с нуля за полиномиальное время, и к тем задачам, решения которых могут быть проверены за полиномиальное время (формальные определения P и NP в главе 23).
Конечно, проверка предложенного кем-то решения судоку или кенкен выглядит проще самостоятельного разбора головоломки. Как и легко проверить, что предложенный кем-то тур коммивояжера является хорошим (с суммарной стоимостью, скажем, не более 1000), просуммировав стоимости его ребер. Не ясно, как быстро можно придумать такой тур с нуля. Поэтому пояснение ниже настаивает: предположение, что P ≠ NP, является истинным.
Более подробно с книгой можно ознакомиться на сайте издательства
» Оглавление
» Отрывок
Для Хаброжителей скидка 25% по купону — Алгоритмы
По факту оплаты бумажной версии книги на e-mail высылается электронная книга.