В предыдущем материале из этой серии мы простыми словами рассказали о том, что такое обучение с подкреплением (Reinforcement learning, RL). Там мы, на интуитивном уровне, разобрались с тем, как работают механизмы RL, поговорили о том, как обучение с подкреплением применяется для решения практических задач. В этом материале мы изучим математический аппарат RL, начав с его базовых принципов и дойдя до примеров применения этих принципов при проектировании RL-алгоритмов.
Компоненты алгоритма обучения с подкреплением
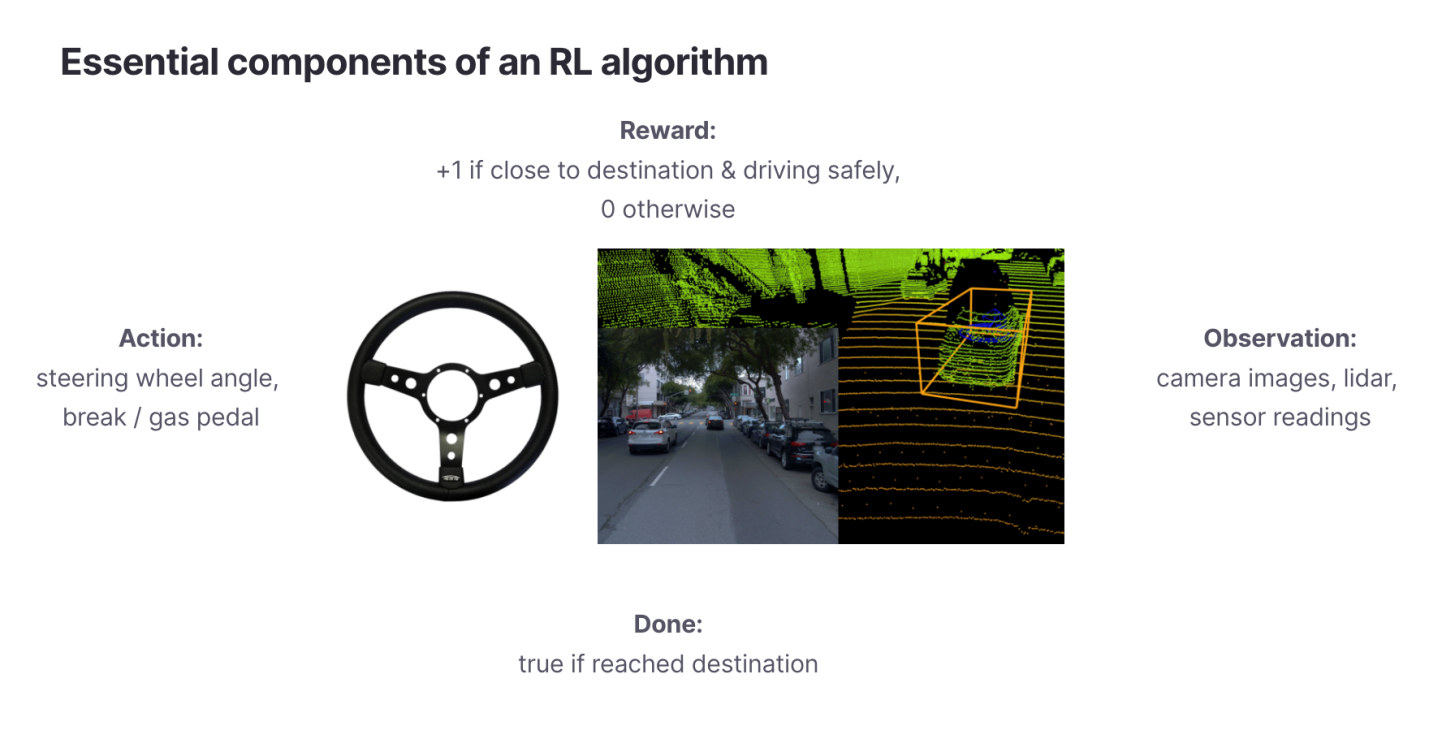
Начнём с постановки задачи. Перед применением алгоритма обучения с подкреплением мы должны определить следующие его свойства:
Пространство наблюдения (observation space),
. Наблюдения — это данные, которые RL-агент использует для познания мира. Беспилотное транспортное средство (Autonomous Vehicle, AV) может наблюдать за миром посредством камер и лидара.Пространство действия (action space),
. Пространство действия определяет то, какие действия может предпринять RL-агент. В пространство действия беспилотного автомобиля может входить поворот рулевого колеса на определённый угол, а так же — использование педалей газа и тормоза.Функция вознаграждения (reward function),
. С использованием функции вознаграждения каждому временному шагу назначают метку, отражающую его вклад в результирующий показатель, который мы стремимся оптимизировать.Конечное условие (terminal condition),
. Конечное условие определяет длительность одного эпизода цикла обучения с подкреплением. Оно выражается либо фиксированным количеством времени (например — 1000 шагов), либо срабатывает по достижении благоприятного исхода некоей последовательности действий (например — когда беспилотный автомобиль благополучно прибыл в пункт назначения, или когда пользователь купил то, что ему предложила рекомендательная система).
Цель алгоритма обучения с подкреплением
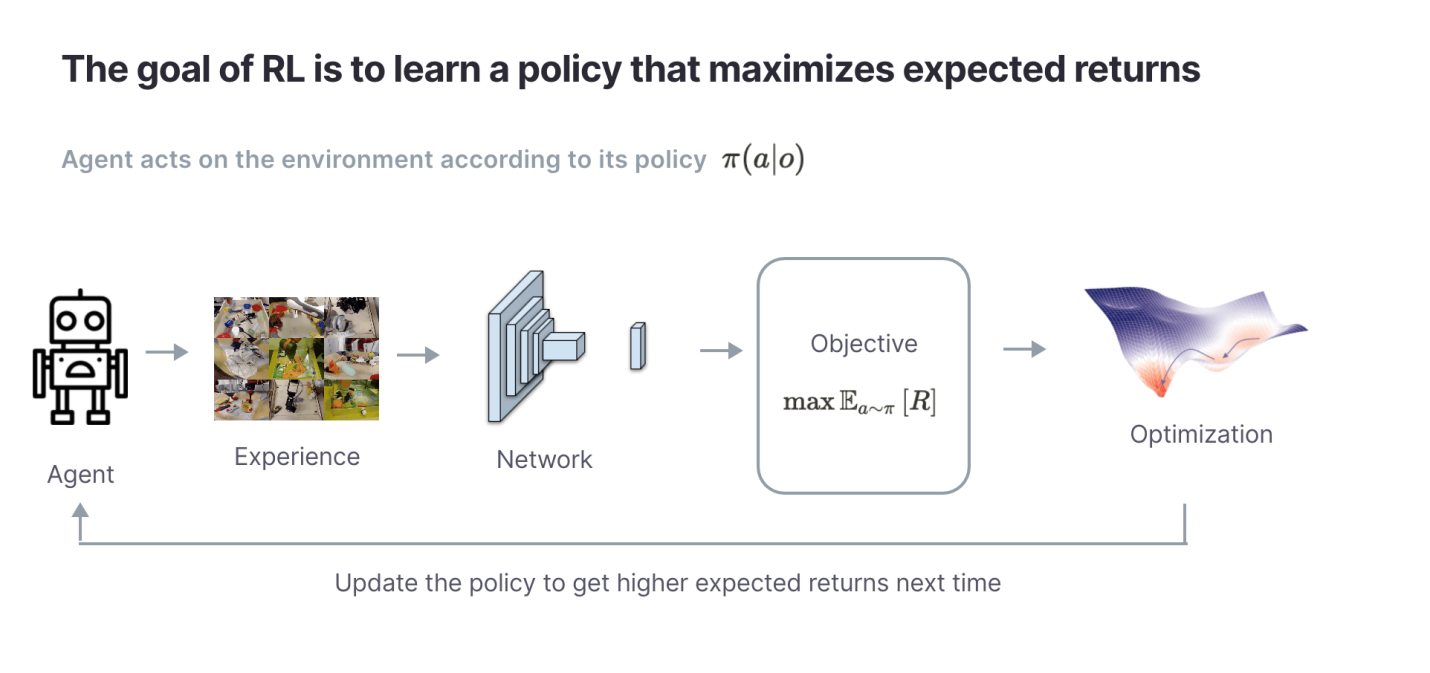
Теперь, когда мы разобрались с постановкой задачи, нам нужно определить то, что именно RL-алгоритм будет оптимизировать. Цель RL-алгоритмов довольно-таки проста: она заключается в том, чтобы найти такие правила поведения (policy), 
, которые максимизируют общие вознаграждения (известные ещё как результаты) 
в эпизоде. На интуитивном уровне понятно, что «правила поведения» — это RL-агент. Правила поведения формируют действие в ответ на текущие наблюдения за окружающей средой, сделанные агентом.
К сожалению, определение текущей цели алгоритма — это разновидность «проблемы курицы и яйца». Для достижения 
RL-агенту нужно видеть будущие результаты, но для того чтобы их видеть, правила поведения агента должны воздействовать на окружение, а значит результаты уже не окажутся «будущими». Каким образом агент может выбрать действие так, чтобы достигнуть 
до того, как он окажет некое реальное влияние на окружающую среду?
Именно тут в дело вступает очень и очень важная концепция ожидаемого результата. RL-агент не максимизирует реальные вознаграждения. Он формирует оценку того, каким в будущем окажется 
в том случае, если он будет действовать в соответствии с 
. Другими словами — цель агента заключается в том, чтобы достигнуть ![max\, \mathbb{E}_{a\sim\pi}\,\left [ R \right ]](https://habrastorage.org/getpro/habr/upload_files/393/698/f45/393698f455bb3e3fb18d3856db7c933f.svg)
, а не 
. Эта концепция ожидаемого результата является центральным элементом всех алгоритмов обучения с подкреплением. В следующем материале из этой серии мы поговорим о том, как вышеозначенная цель ведёт к Q-обучению, а пока мы можем сформулировать главную цель обучения с подкреплением так:
? Цель алгоритма обучения с подкреплением заключается в том, чтобы найти такие правила поведения
, которые позволяют достигнуть максимальных ожидаемых результатов
в окружающей среде, в которой работает алгоритм.
Цикл алгоритма обучения с подкреплением
Определив компоненты и цель RL-алгоритма, мы можем описать цикл обучения с подкреплением. На каждом шаге агент изучает мир, в котором он работает, воздействует на этот мир и получает результат. Этот процесс повторяется до тех пор, пока не будет достигнуто конечное условие 
. Кроме того, агент вносит изменения в правила своего поведения, пользуясь для этого собранными данными. Делается это для того чтобы найти такие правила 
, которые позволяют максимизировать результат.
Тут стоит упомянуть об одной маленькой, но важной детали. Дело в том, что при рассмотрении результата большинство RL-алгоритмов вводят дополнительный параметр 
, называемый коэффициентом дисконтирования (discount factor). Коэффициент дисконтирования ускоряет сходимость RL-алгоритмов, приоритизируя краткосрочные вознаграждения. В итоге результат взвешивают по дисконту — 
Обычно назначают значение, близкое к единице (например — 
) для того, чтобы не допустить «близорукости» алгоритма.
Если попытаться, на интуитивном уровне, понять смысл коэффициента дисконтирования, то окажется, что он задаёт длительность промежутка времени, который рассматривает RL-агент при максимизации результатов. Например — применение коэффициента дисконтирования 
приведёт к тому, что агент будет максимизировать результаты примерно на 100 шагах (так как 100 будет близко к 0). Другими словами — коэффициент дисконтирования — это гиперпараметр, который определяет временные рамки результата, учитываемого агентом. При значениях, близких к нулю, легче выполнять оптимизацию, так как агента заботят лишь краткосрочные результаты. А значения, близкие к единице, заставляют агента максимизировать результаты на длительных промежутках времени. Но это усложняет оптимизацию. Коэффициент дисконтирования используется в большинстве RL-алгоритмов, применяемых для решения практических задач.
? Цель большинства алгоритмов обучения с подкреплением, используемых на практике, заключается в том, чтобы максимизировать ожидаемые дисконтированные результаты:
![max\, \mathbb{E}_{a\sim\pi}\,\left [ R \right ] = max\,\mathbb{E}_{a\sim\pi}\,\left [ \sum_{t} \gamma ^tr_t \right ]](https://habrastorage.org/getpro/habr/upload_files/728/f0c/9ba/728f0c9ba5b933e76dbcc473643aad27.svg)
Итоги
Мы рассмотрели математический аппарат, который используется при проектировании алгоритмов обучения с подкреплением. Тут надо обратить внимание на то, что этот математический аппарат отличается весьма общим характером. Если можно определить пространство наблюдения, пространство действия и функцию вознаграждения — можно создать RL-алгоритм и оптимизировать его параметры так, чтобы он нашёл бы правила поведения, которые максимизируют ожидаемые результаты. Обычно RL-алгоритмы не делают никаких предположений о том, какие конкретные задачи решают с их помощью. Именно поэтому они широко применяются для решения самых разных задач. Среди них — управление беспилотными транспортными средствами, построение рекомендательных систем, выделение ресурсов и много других практических задач.
В следующем материале из этой серии мы поговорим о применении обучения с подкреплением в сетях Deep Q.
О, а приходите к нам работать? ?
Мы в wunderfund.io занимаемся высокочастотной алготорговлей с 2014 года. Высокочастотная торговля — это непрерывное соревнование лучших программистов и математиков всего мира. Присоединившись к нам, вы станете частью этой увлекательной схватки.
Мы предлагаем интересные и сложные задачи по анализу данных и low latency разработке для увлеченных исследователей и программистов. Гибкий график и никакой бюрократии, решения быстро принимаются и воплощаются в жизнь.
Сейчас мы ищем плюсовиков, питонистов, дата-инженеров и мл-рисерчеров.
