Алгоритмы *

Пост №1. Что такое SOINN


SOINN – это самоорганизующаяся инкрементная нейронная сеть. Структура и алгоритм такой нейронной сети повидимому хорошо себя зарекомендовал в японской лаборатории Hasegawa (сайт — haselab.info), потому что он в итоге был взят за основу и дальнейшее развитие алгоритмов искусственного интеллекта шло путем небольших модификаций и надстроек к сети SOINN.

Базовая сеть SOINN состоит из двух слоев. Сеть получает входной вектор и на первом слое после обучения создает узел (нейрон) – определяющий класс для входных данных. Если входной вектор похож на существующий класс (мера похожести определяется настройками алгоритма обучения) то два самых похожих нейрона первого слоя объединяются связью, либо если входной вектор не похож не на один существующей класс, то в первом слое создается новый нейрон, определяющий текущий класс. Очень похожие нейроны первого слоя, объединенные связью, определяются как один класс. Первый слой является входным слоем для второго слоя, и по аналогичному алгоритму, с небольшим исключением, создаются классы во втором слое.

На основе SOINN созданы такие сети, как (далее представлены название сети и описание сети от ее создателей):

Как же все-таки работает HTTPS? Это вопрос, над которым я бился несколько дней в своем рабочем проекте.

Будучи Web-разработчиком, я понимал, что использование HTTPS для защиты пользовательских данных – это очень и очень хорошая идея, но у меня никогда не было кристального понимания, как HTTPS на самом деле устроен.

Как данные защищаются? Как клиент и сервер могут установить безопасное соединение, если кто-то уже прослушивает их канал? Что такое сертификат безопасности и почему я должен кому-то платить, чтобы получить его?

В 2012 году вся общественность, более или менее причастная к информационной безопасности, пристально следила за выборами нового стандарта хеширования данных SHA-3. На хабре достаточно широко освещалось это важное событие: публиковались результаты каждого раунда конкурса (раз, два, три), приводилось описание нового стандарта, и даже объяснялось почему новый стандарт так крут.
Однако, за всем этим ажиотажем совсем незамеченным осталось другое, не менее значимое событие: 1 января 2013 года в РФ также сменился стандарт хеш-функции.
Итак, встречайте: полное описание нового стандарта и его реализация на C#. Как говорится, лучше поздно, чем никогда.

Эта статья рассказывает о времени выполнения и о расходе памяти большинства алгоритмов используемых в информатике. В прошлом, когда я готовился к прохождению собеседования я потратил много времени исследуя интернет для поиска информации о лучшем, среднем и худшем случае работы алгоритмов поиска и сортировки, чтобы заданный вопрос на собеседовании не поставил меня в тупик. За последние несколько лет я проходил интервью в нескольких стартапах из Силиконовой долины, а также в некоторых крупных компаниях таких как Yahoo, eBay, LinkedIn и Google и каждый раз, когда я готовился к интервью, я подумал: «Почему никто не создал хорошую шпаргалку по асимптотической сложности алгоритмов? ». Чтобы сохранить ваше время я создал такую шпаргалку. Наслаждайтесь!

55-летний американский математик Тереза Кристи (Theresa Christy) работает в компании Otis Elevator Co. и считается одним из лучших специалистов по вертикальному транспорту. Двадцать пять лет своей жизни она посвятила разработке и оптимизации алгоритмов для лифтов. Именно её привлекли во время недавней реконструкции Empire State Building стоимостью $550 млн. Тереза Кристи увеличила скорость лифтов на 20% до 6 м/c, так что они теперь проходят первые 80 этажей всего за 48 секунд.

TCP (Transmission Control Protocol) — основной протокол интернета. Одна из его главных задач — бороться с перегрузками в сети (network congestion), когда возникают заторы из пакетов. Регулирование осуществляется путём взаимной подстройки скорости отправки запросов, причём для этого существует множество хитрых методов. Например, в Linux используется алгоритм под названием TCP Cubic, а под Windows — Compound TCP. Кроме них, существуют ещё TCP Tahoe, Reno, NewReno, Vegas, FAST, BIC и др.

Специалисты из Массачусетского технологического института разработали программу Remy, которая методом проб и ошибок пыталась улучшить существующие алгоритмы подавления заторов TCP. Результат превзошёл все ожидания. Эффективность алгоритмов RemyCC превзошла и TCP Cubic, и Compound TCP, и остальных «конкурентов» в различных сетевых условиях. Проблема только в том, что учёные не совсем понимают, за счёт чего именно Remy удалось показать такой феноменальный результат.

Disclaimer Данная статья публикуется исключительно в ознакомительных целях, за использование материалов, опубликованных в данной статье автор ответственности не несет.
Так же хочу сразу предупредить, что если вы рассчитываете найти в этой статье пошаговое руководство к прослушиванию GSM трафика или надеетесь, прочитав данную статью, получить доступ к телефонным разговорам ваших друзей, знакомых, домашних животных, то лучше проигнорируйте ее. Здесь вы не найдете ничего интересного. Нет правда, не ходите под кат, там скука.

Доброго времени суток, уважаемые! К сожалению, из-за больничного режима, я не мог последний месяц опубликовать своё очередное изыскание на тему игры «Морской бой». Надеюсь, моя заметка окажется для кого-то полезной, и, даже если и будет частичным повторением, то в новой интерпретации.
Итак, сегодня я хотел бы обсудить вопрос расстановки (не оптимальной, а произвольной) кораблей перед боем. Слева вы видите пример результата работы рассматриваемого далее алгоритма: корабли в форме букв «R», «A», «H», «B» расставлены на игровом поле размером 5х15 с несколькими запрещёнными к использованию клетками (помечены зелёным цветом). Заинтересовавшихся прошу под кат.

«Бросая в воду камешки, смотри на круги, ими образуемые; иначе такое бросание будет пустою забавою.»
К.Прутков

Однажды, бесцельно тратя рабочее время и деньги работодателя с помощью серфинга интернета, наткнулся я на описание языка Whenever и на некоторое время был очарован. Язык поражает своей безумной простотой. Принципы его таковы:

1) Строки кода программы обязательно будут исполнены когда-нибудь, однако порядок их исполнения вообще никак не связан с порядком, в котором они записаны.
2) Переменные? У нас нету даже контроля за порядком исполнения, нам не нужны никакие переменные.
3) Структуры данных? Да вы шутите!

То есть программа трактуется как набор (пул) строк на выполнение и интерпретатор выбирает оттуда строку наугад, выполняет ее команды и выкидывает из пула. И так пока в пуле ничего не останется. Надо признать, что автор сего безумия почти выдержал концепцию. Почти, потому что все же организовать порядок выполнения в программе можно, так же, как и завести переменные, используя возможность добавления строк в пул выполняемых.

Наверное все, кто хоть чуть-чуть работал с фотошопом — видели эффект outer glow для слоя, и пробовали с ним играться. В фотошопе есть 2 техники этого самого outer glow. Soft и precise. Soft мне был не так интересен, а вот глядя на precise — я задумался.

Выглядит он вот так:

Это однопиксельная линия. А градиент грубо говоря — отражает расстояние до ближайшего пикселя изображения. Это самое расстояние — могло бы быть очень вкусным для построения разнообразных эффектов. Это и всякие контуры, и собственные градиенты, и
Основная проблема такого glow — это сложность вычисления для больших размеров. Если у нас glow на 100 пикселей, то нам надо для каждого пикселя изображения проверить 100*100 соседних пикселей. И для изображения например 800*600 это будет всего 4 800 000 000 проверок.

Однако фотошоп этим не страдает, и прекрасно строит точный glow даже больших (до 250) размеров. Значит решение есть. И мне любопытно было его найти. Нагуглить быстрый алгоритм такого glow у меня не получилось. Большинство алгоритмов использует blur чтобы построить glow, но мы то с вами знаем, что однопиксельная линия не даст нам такого эффекта, как на картинке, она просто сблюрится.

Поэтому я погнал велосипедить.

На прошедшем неделю назад чемпионате мира по командному программированию ACM ICPC 2013 было 11 задач, одну из которых за отведённое время не смогла решить правильно ни одна из команд.

Но кроме команд есть и другие люди, которые профессионально решают задачи, — аналитики чемпионата. В течение трансляции они разбиваются на группы, распределяют задачи и потом рассказывают о них в студии. Множество зрителей следят за эфиром, пока эти ребята не разберут самую последнюю задачу. Кроме того, аналитики подсказывают ведущему, что происходит «на поле», высматривают интересные куски кода, следят за картинкой с веб-камер участников.

В этом году на ACM ICPC был 21 аналитик из Швеции, Нидерландов, США, Словакии, Беларуси и России. И 10 из них были из Яндекса. Все они в разные годы были призёрами ICPC. Специально для Хабра они разобрали все задания чемпионата.

С текстурами вечно какие-то проблемы! То оказывается, что нельзя взять любую фотку и налепить на модельку. То на стыке текстур появляются швы, которые замучаешься заглаживать. То вроде уже и загладил всё, но глаз, этакий проказник, всё равно замечает повторяющиеся узоры и рушит иллюзию.

Можно сделать текстуру побольше, чтобы повторяющиеся куски дальше отстояли друг от друга и были не так заметны. Можно даже сделать её совсем огромной, на пару сотен тысяч пикселей, чтобы она накрывала всю сцену целиком без швов и повторений. Подобную технику называют мегатекстурой. Но мегатекстуры и близкие к ним виртуальные текстуры усложняют работу с памятью, для работы с ними требуются особые инструменты, да и в целом это ещё молодая технология.

Как же быть? Есть один трюк — непериодические мозаики. Они лишены проблемы повторяемости и достаточно просты в реализации. Одну из таких мозаик придумал китайский математик Ван Хао в 1961 году. Элементы этой мозаики можно представить в виде прямоугольников с разноцветными гранями. Но чтобы понять принцип её работы, надо сначала разобраться в классическом методе заполнения площадей текстурами.

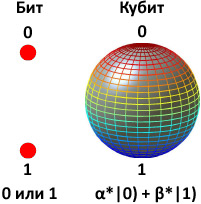Хотя квантовые компьютеры существуют пока только в теории, но это не мешает делать обоснованные предположения об их будущей архитектуре и, что более важно, об интерфейсе взаимодействия с ними. Таким образом, уже сейчас есть возможность проектировать программные симуляторы квантовых компьютеров — и писать софт.

Группа американских учёных, получив финансирование от исследовательского центра Национальной разведки США (IARPA) разработала высокоуровневый язык программирования Quipper. Он создан на основе Haskell и лучше подходит для реализации квантовых алгоритмов, чем QCL (основан на C).

На сегодняшний день известно как минимум 45 алгоритмов для квантовых компьютеров. Все они описаны в научных статьях, но ни один не был реализован в программном коде. С появлением Quipper появилась такая возможность. В дальнейшем программисты смогут просто использовать готовые библиотеки для квантовых компьютеров, как они это делают сейчас на высокоуровневых языках для классической архитектуры.

Недавно на хабре проскочил пост, который напомнил мне о такой забавной и довольно интересной вещи, как BoxCar2D (Оригинал, Версия из поста), которую в первый раз я увидел пару лет назад, и которая меня порядком впечатлила. И уже тогда я подметил в ней один фатальный недостаток (вкратце — ее сделал не я), но в тот раз руки так и не дошли до его исправления. И вот теперь я решил это исправить.

Итак, я расчехлил Visual Studio и принялся за дело.
Первым делом я просто повторил функционал BoxCar2D, а именно: фиксированный размер популяции, которая проживает свою жизнь и порождает следующее поколение. Можно было поиграться с тем, как усложняется трасса со временем, что содержит в себе геном и как машинки скрещиваются и мутируют.

Французская компания Spotter разработала инструмент, который, по их словам, способен идентифицировать сарказм в комментариях в Интернете.

Созданная программная платформа сканирует социальные медиа и другие интернет-источники для создания отчетов о репутации своих клиентов — среди которых есть Европейская комиссия, Air France и другие крупные заказчики. Как и большая часть подобного ПО, приложение занимается анализом семантики, лингвистики и эвристики. Однако, как и любая другая система с машинным анализом данных, их инструмент часто испытывает проблемы с такими тонкими частями человеческой речи, как сарказм и ирония — и, вроде бы, как раз эту проблему Spotter и удалось преодолеть — пусть их руководители и признают, что результат пока что далек от идеального, и что полностью доверять машине еще рано. Процент распознавания достигает 80%, и, по заявлению авторов, еще несколько лет назад даже подобный результат был немыслим — тогда сарказм опознавался в 50% случаев. Авторы говорят, что алгоритм работает с 29 языками (включая русский и китайский), а чаще всего им приходится иметь дело с распознаванием сообщений о плохом уровне обслуживания.

На что вы сейчас смотрите? Если вы не из параллельной вселенной, где все сидят за векторными мониторами, то перед вами растровое изображение. Поглядите на эту полоску: /. Если придвинуться поближе к монитору, то можно увидеть пиксельные ступеньки, которые пытаются притвориться векторной линией. Для этой цели существует целая куча всевозможных алгоритмов растеризации, но я бы хотел рассказать об алгоритме Брезенхема и алгоритме У, которые находят приближение векторного отрезка в растровых координатах.

С проблемой растеризации мне довелось столкнуться во время работы над процедурным генератором планов зданий. Мне нужно было представить стены помещения в виде ячеек двумерного массива. Похожие задачи могут встретиться в физических расчётах, алгоритмах поиска пути или расчёте освещения, если используется разбиение пространства. Кто бы мог подумать, что знакомство с алгоритмами растеризации однажды может пригодиться?

Несмотря на некоторый скепсис, по поводу первой части материала, как и обещал, публикую результаты, и то как они были получены.
В основном манипуляции производились с данными, хранимыми в Excell, таблицы которого сформированы по 3НФ, поэтому в некоторых местах кода вместо индексов используются данные из ячеек. Итак согласно алгоритму необходимо получить коэффициент клуба и климатическую характеристику города, в котором этот клуб принимает соперников = команда: {климат, рейтинг} — это и есть основная цель. Поехали.

«Как автоматизировать сочинение музыки?» — этот вопрос тревожит умы музыкантов еще со времен средневековья. Кеплер превращал траектории движения планет в музыку; Моцарт и его современники изобрели игру в «музыкальные кости» — они броском кубиков выбирали из большой таблицы такты и составляли из них менуэты. Но только с появлением компьютеров алгоритмическая генерация музыки получила настоящее развитие. Теория вероятности, марковские цепи, искусственные нейронные сети — все это стало инструментами создания музыки.

Однажды после переезда пришлось озадачиться поиском своего почтового отделения. В последних версиях настольной версии 2Гис, к счастью, для большинства городов имеется информация об индексах зданий и в конечном итоге поиск свелся к выбору почтового отделения по номеру, равному последним трем цифрам индекса, однако число рутинных операций для этого было достаточно велико и захотелось на досуге в качестве разминки для ума и из любви к прикладным алгоритмам попытаться этот процесс автоматизировать.

Вступление

Эта реализация игры «Уголки» на JavaScript, созданная в целях обучения. Игровой процесс заключается в том, что бы переместить свои фишки из одного угла игрового поля в другое (по определенным правилам) быстрее противника. В этой реализации четыре режима: игра компьютерных игроков, игра с компьютерным игроком, мультиплеер на одном компьютере и мультиплеер по сети.