Решил написать статью про алгоритм параллельного поиска максимально возможных пересечений двух строк. К написанию этой статьи меня побудило два желания:
Все началось с конкурса, проводимого Intel, о котором я узнал из поста. Суть конкурса сводилась к разработке и реализации алгоритма, решающего задачу нахождения в двух строках максимально длинной общей подстроки (переписывать полностью задачу сюда, думаю, не имеет смысла). К той задачке прилагался референсный код, т.е. решение на которое надо было «равняться». Чуть позже, из форума, посвященному этому конкурсу, стало понятно, что референсный код не решает эту задачу в том виде в котором она сформулирована на сайте Intel. Т.е. весь смысл конкурса сводился к следующему: «сделать программу, которая в точности повторяет вывод референсного кода, при одинаковых входных параметрах, только чтобы она была быстрее и параллельнее».
Ну да ладно, даже несмотря на абсурдность ситуации с описанием задачи, участие в конкурсе я сразу отбросил еще и потому что там могли участвовать только студенты и выпускники. Мне понравилась сама задача, та что описана на сайте.
Вот как я понял из описания эту задачу:
Есть две строки S1 и S2, нужно найти максимально длинную общую подстроку(и) (далее будем называть искомые подстроки — подмножествами), длина которой не меньше M. В качестве результата вывести ее координаты.
Координатами являются четыре целых числа.
Первые два относятся к строке S1 — это номера позиций первого и последнего символов найденной подстроки.
Вторые два числа имеют тоже значение, только относятся ко второй строке — S2.
Например, если мы имеем следующие входные параметры:
S1 = ABCCA
S2 = ACCABABCCBAABCBAABCBACBACBACBAC
M = 2
то ответом будет:
0 3 5 8
(в оригинальной постановки задачи координаты требуется выводить начиная с 1, но это уже детали вывода результата, и они никак не относится к самому алгоритму).
Также в требованиях к задаче указывается еще один дополнительный входной параметр K — число потоков, которое можно использовать для распаралеливания алгоритма.
Срезюмируем то что нам дается на вход:
По сути, идея решения очень проста и состоит из 3-х шагов:
Рассмотрим работу алгоритма на следующем примере:
S1 = ABCCA
S2 = ACCABABCCBAABCBAABCBACBACBACBAC
M = 2
K = 2
1) Разбиваем S1 на сегменты, каждый длиной M = 2:
AB, BC, CC, CA
2) Проецируем каждый полученный сегмент на S2:

или в виде смещений:

таким образом мы получили проекцию S1 на S2:

дальше будем называть эту проекцию — картой пересечений.
По сути, карта пересечений представляет из себя матрицу координат всех сегментов длина которых равна M. Т.е. каждый элемент матрицы характеризует координату в строке S2, в то время как номер строки матрицы характеризует координату в строке S1. Имея в распоряжении карту пересечений, мы можем найти все пересечения (подмножества) и выбрать из них максимальные.
3) Производим поиск максимальных подмножеств (совокупность сегментов).
Если посмотреть на карту пересечений в символьном виде, то уже визуально можно найти максимально длинное подмножество:
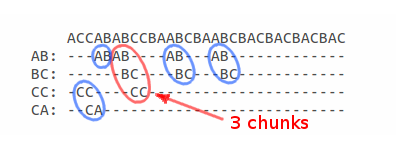
если брать во внимание что каждый сегмент может служить началом подмножества, то используя карту пересечений, можно вычислить длину всех подмножеств, началом которых, являются сегменты составляющие эту проекцию.
Следующая иллюстрация демонстрирует, как производится вычисление длины подмножества, началом которого служит сегмент с координатой 5:

т.е. подмножество начинающееся с координаты 5 имеет максимальную длину — len = 4, для подмножества начинающегося с координаты 3 длина будет равна 2 и т.д.
Аналогичным образом, пробегая по каждому сегменту в карте пересечений, мы находим, что максимально длинным подмножеством является подмножество длиной 4 с координатами в S1 и S2 строках: 0 и 5 соответственно.
Как можно было заметить каждый шаг в решении этой задачи (шаги 1, 2, 3) легко распараллеливается, возможно применение Map-Reduce.
1, 2) Каждому потоку назначается свой сегмент (или несколько сегментов), для которого он строит проекцию сегмента. В совокупности, после того как для всех сегментов будут получены соответствующие проекции, получим готовую карту пересечений.

3.1) Каждому потоку назначается свой порядковый номер (n). Далее n-ый поток, начиная c n-ой позиции, обрабатывает каждый K-ый элемент карты пересечений. Таким образом мы разбиваем карту пересечений на несколько (число потоков) частей. Из этих частей, выбирают, вышеописанным образом, максимальные подмножества:
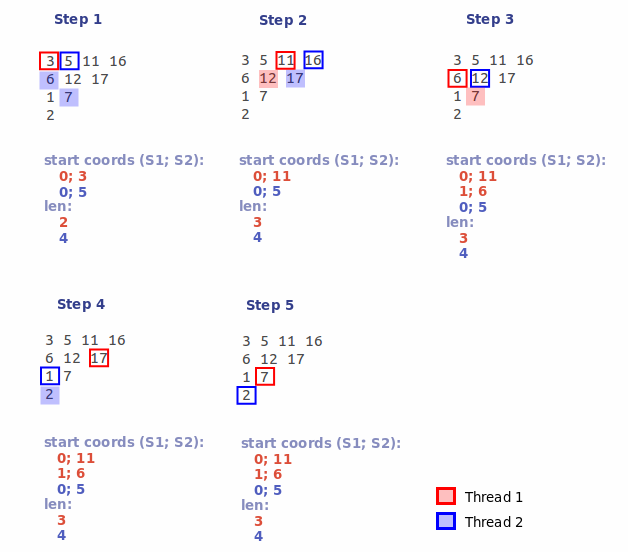
3.2) После того как все потоки отработают, мы получим несколько групп подмножеств. Из полученных групп выбираем группы с максимальной длиной сегментов. В нашем примере это две группы: группа образованная потоком #1, содержащая в себе сегменты длиной 3 символа (с начальными координатами: 0; 11 и 1; 6), а также группа образованная потоком #2, содержащая в себе один сегмент длиной 4 символа (с координатами 0; 5). Поскольку вторая группа имеет наибольшую длину сегментов, то первую группу отбрасываем сразу.
В результате мы получили начальные координаты подмножества (0; 5) и его длину — 4. Для нахождения конечных координат применяем формулу: end_coord = start_coord + len — 1.
Таким образом получаем ответ: 0 3 5 8.
Я решил не затрагивать рассмотрение деталей реализации, данного алгоритма на С++, так как это уже выходит за рамки данной статьи. Ознакомится с реализацией данного алгоритма на С++ (С++11) можно здесь, для компиляции при помощи GCC не забываем ставить флаги -pthread и -std=с++0X.
Этот алгоритм пришел мне в голову как очевидное решение задачи, но я не знаю, есть ли у него официальное название и/или формальное описание?
- Поделиться со всеми интересным алгоритмом и его реализацией на С++ (стандарт С++11);
- Узнать, есть ли у данного алгоритма название и/или формальное описание;
Предыстория
Все началось с конкурса, проводимого Intel, о котором я узнал из поста. Суть конкурса сводилась к разработке и реализации алгоритма, решающего задачу нахождения в двух строках максимально длинной общей подстроки (переписывать полностью задачу сюда, думаю, не имеет смысла). К той задачке прилагался референсный код, т.е. решение на которое надо было «равняться». Чуть позже, из форума, посвященному этому конкурсу, стало понятно, что референсный код не решает эту задачу в том виде в котором она сформулирована на сайте Intel. Т.е. весь смысл конкурса сводился к следующему: «сделать программу, которая в точности повторяет вывод референсного кода, при одинаковых входных параметрах, только чтобы она была быстрее и параллельнее».
Ну да ладно, даже несмотря на абсурдность ситуации с описанием задачи, участие в конкурсе я сразу отбросил еще и потому что там могли участвовать только студенты и выпускники. Мне понравилась сама задача, та что описана на сайте.
Постановка задачи
Вот как я понял из описания эту задачу:
Есть две строки S1 и S2, нужно найти максимально длинную общую подстроку(и) (далее будем называть искомые подстроки — подмножествами), длина которой не меньше M. В качестве результата вывести ее координаты.
Координатами являются четыре целых числа.
Первые два относятся к строке S1 — это номера позиций первого и последнего символов найденной подстроки.
Вторые два числа имеют тоже значение, только относятся ко второй строке — S2.
Например, если мы имеем следующие входные параметры:
S1 = ABCCA
S2 = ACCABABCCBAABCBAABCBACBACBACBAC
M = 2
то ответом будет:
0 3 5 8
(в оригинальной постановки задачи координаты требуется выводить начиная с 1, но это уже детали вывода результата, и они никак не относится к самому алгоритму).
Также в требованиях к задаче указывается еще один дополнительный входной параметр K — число потоков, которое можно использовать для распаралеливания алгоритма.
Срезюмируем то что нам дается на вход:
- S1, S2 — две строки, в которых необходимо произвести поиск;
- M — минимально возможная длина искомой подстроки;
- K — число потоков которое можно использовать для распаралеливания;
Алгоритм
По сути, идея решения очень проста и состоит из 3-х шагов:
- Разбить S1 на минимально-возможные (длиной M) сегменты.
- Спроецировать сегменты на S2.
- На полученной проекции, найти максимально длинные подмножества (состоящие из максимального количества подряд идущих сегментов).
Рассмотрим работу алгоритма на следующем примере:
S1 = ABCCA
S2 = ACCABABCCBAABCBAABCBACBACBACBAC
M = 2
K = 2
1) Разбиваем S1 на сегменты, каждый длиной M = 2:
AB, BC, CC, CA
2) Проецируем каждый полученный сегмент на S2:

или в виде смещений:

таким образом мы получили проекцию S1 на S2:

дальше будем называть эту проекцию — картой пересечений.
По сути, карта пересечений представляет из себя матрицу координат всех сегментов длина которых равна M. Т.е. каждый элемент матрицы характеризует координату в строке S2, в то время как номер строки матрицы характеризует координату в строке S1. Имея в распоряжении карту пересечений, мы можем найти все пересечения (подмножества) и выбрать из них максимальные.
3) Производим поиск максимальных подмножеств (совокупность сегментов).
Если посмотреть на карту пересечений в символьном виде, то уже визуально можно найти максимально длинное подмножество:
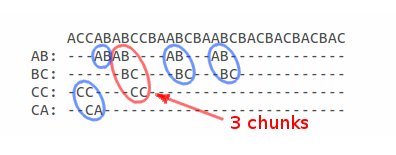
если брать во внимание что каждый сегмент может служить началом подмножества, то используя карту пересечений, можно вычислить длину всех подмножеств, началом которых, являются сегменты составляющие эту проекцию.
Следующая иллюстрация демонстрирует, как производится вычисление длины подмножества, началом которого служит сегмент с координатой 5:

т.е. подмножество начинающееся с координаты 5 имеет максимальную длину — len = 4, для подмножества начинающегося с координаты 3 длина будет равна 2 и т.д.
Аналогичным образом, пробегая по каждому сегменту в карте пересечений, мы находим, что максимально длинным подмножеством является подмножество длиной 4 с координатами в S1 и S2 строках: 0 и 5 соответственно.
Распараллеливание
Как можно было заметить каждый шаг в решении этой задачи (шаги 1, 2, 3) легко распараллеливается, возможно применение Map-Reduce.
1, 2) Каждому потоку назначается свой сегмент (или несколько сегментов), для которого он строит проекцию сегмента. В совокупности, после того как для всех сегментов будут получены соответствующие проекции, получим готовую карту пересечений.

3.1) Каждому потоку назначается свой порядковый номер (n). Далее n-ый поток, начиная c n-ой позиции, обрабатывает каждый K-ый элемент карты пересечений. Таким образом мы разбиваем карту пересечений на несколько (число потоков) частей. Из этих частей, выбирают, вышеописанным образом, максимальные подмножества:
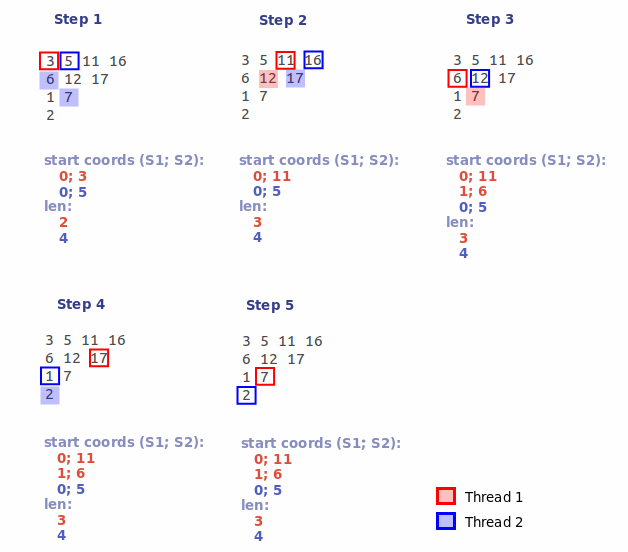
3.2) После того как все потоки отработают, мы получим несколько групп подмножеств. Из полученных групп выбираем группы с максимальной длиной сегментов. В нашем примере это две группы: группа образованная потоком #1, содержащая в себе сегменты длиной 3 символа (с начальными координатами: 0; 11 и 1; 6), а также группа образованная потоком #2, содержащая в себе один сегмент длиной 4 символа (с координатами 0; 5). Поскольку вторая группа имеет наибольшую длину сегментов, то первую группу отбрасываем сразу.
В результате мы получили начальные координаты подмножества (0; 5) и его длину — 4. Для нахождения конечных координат применяем формулу: end_coord = start_coord + len — 1.
Таким образом получаем ответ: 0 3 5 8.
Заключение
Я решил не затрагивать рассмотрение деталей реализации, данного алгоритма на С++, так как это уже выходит за рамки данной статьи. Ознакомится с реализацией данного алгоритма на С++ (С++11) можно здесь, для компиляции при помощи GCC не забываем ставить флаги -pthread и -std=с++0X.
Вопрос
Этот алгоритм пришел мне в голову как очевидное решение задачи, но я не знаю, есть ли у него официальное название и/или формальное описание?
















