
Процедурная генерация — замечательная штука! Интереснее всего работать именно с графикой, особенно трёхмерной — сразу видно результат. Всего пары инструкций достаточно, чтобы создать облако треугольников как на картинке выше.
Процедурная генерация моделей может помочь сэкономить размер дистрибутива, добавить кастомизацию игровых персонажей, на худой конец её просто можно использовать для создания спецэффектов.
На примере движка Unity и C# я покажу как можно работать с моделями и превращать текст в графику. Большинство приводимого кода легко портируется на другие фреймфорки и языки.
Треугольник
Начнём с простейшей формы — треугольника. В Unity и во многих других движках используется популярный способ описания моделей: с помощью массивов вершин, треугольников и нормалей. Дополнительно для текстурирования используются uv-координаты вершин. Для работы с моделями есть класс Mesh, в котором для каждого набора данных имеется отдельный массив. В Mesh.vertices хранятся координаты вершин, в Mesh.triangles — индексы вершин группами по три. А в Mesh.normals и Mesh.uv лежат векторы нормалей и координаты uv-карт, индексы которых должны совпадать с индексами соответствующих вершин, т. е. порядок в массивах должен быть одинаковым. Покажу на примере, чтобы было понятнее.
Сделаем функцию, которая на вход принимает три вершины треугольника, а отдаёт готовую модельку. Начнём с основы.
public static Mesh Triangle(Vector3 vertex0, Vector3 vertex1, Vector3 vertex2)
{
var mesh = new Mesh();
mesh.vertices = new [] {vertex0, vertex1, vertex2};
mesh.triangles = new [] {0, 1, 2};
return mesh;
}
Упаковываем три вершины в массив и передаём мешу. Треугольник описывается элементарно, но есть нюанс, про который нужно помнить. Если смотреть на модель снаружи, то вершины её треугольников должны располагаться по часовой стрелке. Это сделано для того, чтобы во время отрисовки можно было отсечь треугольники, которые «не смотрят в камеру», и обрабатывать их отдельно. Порядок вершин рассчитывается очень просто, поэтому такой способ фильтрации очень эффективен. Если взять произведение двух векторов, то можно найти третий вектор, перпендикулярный плоскости, образуемой сомножителями. Если пробежаться по треугольнику и посчитать произведения, то можно узнать порядок вершин. Кстати эти перпендикулярные вектора нам тоже нужны для описания моделей — это ведь нормали. Нормаль считается следующим образом:
var normal = Vector3.Cross((vertex1 - vertex0), (vertex2 - vertex0)).normalized;
Сначала сделали из трёх точек два вектора, а потом перемножили. Эта нормаль будет одинаковой на всех вершинах треугольника.
mesh.normals = new [] {normal, normal, normal};
Осталось добавить uv-координаты, для трёх вершин это просто.
mesh.uv = new [] {new Vector2(0, 0), new Vector2(0, 1), new Vector2(1, 1)};
Ну и всё, треугольник готов. Теперь его можно использовать.
Треугольник
public static Mesh Triangle(Vector3 vertex0, Vector3 vertex1, Vector3 vertex2)
{
var normal = Vector3.Cross((vertex1 - vertex0), (vertex2 - vertex0)).normalized;
var mesh = new Mesh
{
vertices = new [] {vertex0, vertex1, vertex2},
normals = new [] {normal, normal, normal},
uv = new [] {new Vector2(0, 0), new Vector2(0, 1), new Vector2(1, 1)},
triangles = new [] {0, 1, 2}
};
return mesh;
}
Четырёхугольник

Помимо треугольников есть ещё один популярный примитив для моделирования — четырёхугольник, ну или квад, если вам так больше нравится.
Описать четырёхугольник капельку сложнее, нужно добавить одну вершину с её характеристиками и дополнительный треугольник. Я немного изменил входные параметры по сравнению с треугольником, теперь нужно указывать левый нижний угол и две стороны, с настоящими квадами Mesh в Unity всё равно не работает.
Напоминаю, что вершины по-прежнему записываются по часовой стрелке.
Четырёхугольник
public static Mesh Quad(Vector3 origin, Vector3 width, Vector3 length)
{
var normal = Vector3.Cross(length, width).normalized;
var mesh = new Mesh
{
vertices = new[] { origin, origin + length, origin + length + width, origin + width },
normals = new[] { normal, normal, normal, normal },
uv = new[] { new Vector2(0, 0), new Vector2(0, 1), new Vector2(1, 1), new Vector2(1, 0) },
triangles = new[] { 0, 1, 2, 0, 2, 3}
};
return mesh;
}
Теперь, когда мы имеем два базовых примитива, мы можем собрать любую модель.
Плоскость
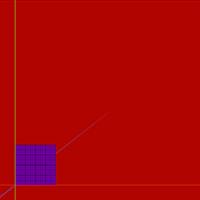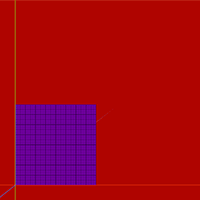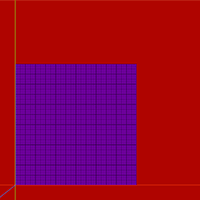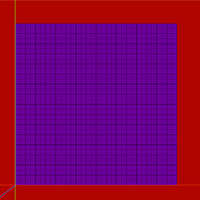
Поэкспериментируем со сборкой моделей на примере плоскости. Возьмём много квадратов и разложим стык в стык.
Лень — двигатель прогресса, поэтому для сборки квадратов в модель будем использовать Mesh.CombineMeshes. Этот метод принимает на вход структуру CombineInstance, в которой можно указать модельку, её индекс и матрицу трансформирования. Для нас важно только первое, остальное игнорируем.
На вход метода подаётся стартовая позиция плоскости, ширина и длина сегмента, количество сегментов. В двойном цикле все квадраты складываются в массив CombineInstance, после чего массив собирается в готовую модель.
Плоскость
public static Mesh Plane(Vector3 origin, Vector3 width, Vector3 length, int widthCount, int lengthCount)
{
var combine = new CombineInstance[widthCount * lengthCount];
var i = 0;
for (var x = 0; x < widthCount; x++)
{
for (var y = 0; y < lengthCount; y++)
{
combine[i].mesh = Quad(origin + width * x + length * y, width, length);
i++;
}
}
var mesh = new Mesh();
mesh.CombineMeshes(combine, true, false);
return mesh;
}
Параллелепипед

Раскладывать плитки по плоскости слишком просто, пора перейти к третьему измерению.
Из квадратов хорошо получаются кубы. Даже лучше, с помощью наших псевдоквадов можно делать не только кубы, но и параллелепипеды. Только тссс! Никому не говорите.
Нужно всего шесть четырёхугольников. Зная длину, ширину и высоту параллелепипеда, можно рассчитать все его вершины. Удобно сначала найти два противоположных угла параллелепипеда, а потом от них отстраивать всё остальное. Также имеет смысл отцентрировать модель. Как это выглядит на практике можете посмотреть ниже.
Параллелепипед
public static Mesh Cube(Vector3 width, Vector3 length, Vector3 height)
{
var corner0 = -width/2 - length/2 - height/2;
var corner1 = width/2 + length/2 + height/2;
var combine = new CombineInstance[6];
combine[0].mesh = Quad(corner0, length, width);
combine[1].mesh = Quad(corner0, width, height);
combine[2].mesh = Quad(corner0, height, length);
combine[3].mesh = Quad(corner1, -width, -length);
combine[4].mesh = Quad(corner1, -height, -width);
combine[5].mesh = Quad(corner1, -length, -height);
var mesh = new Mesh();
mesh.CombineMeshes(combine, true, false);
return mesh;
}
Октаэдр
Октаэдр во многом похож на куб, его вершины очень легко рассчитать, самая большая сложность — сообразить порядок вершин в треугольниках. Октаэдр вписывается в сферу, поэтому имеет смысл строить его по радиусу этой сферы. Все вершины элементарно создаются, так что я не буду здесь останавливаться
Октаэдр
public static Mesh Octahedron(float radius)
{
// Верх
var v0 = new Vector3(0, -radius, 0);
// Многоугольник посередине
var v1 = new Vector3(-radius, 0, 0);
var v2 = new Vector3(0, 0, -radius);
var v3 = new Vector3(+radius, 0, 0);
var v4 = new Vector3(0, 0, +radius);
// Низ
var v5 = new Vector3(0, radius, 0);
var combine = new CombineInstance[8];
combine[0].mesh = Triangle(v0, v1, v2);
combine[1].mesh = Triangle(v0, v2, v3);
combine[2].mesh = Triangle(v0, v3, v4);
combine[3].mesh = Triangle(v0, v4, v1);
combine[4].mesh = Triangle(v5, v2, v1);
combine[5].mesh = Triangle(v5, v3, v2);
combine[6].mesh = Triangle(v5, v4, v3);
combine[7].mesh = Triangle(v5, v1, v4);
var mesh = new Mesh();
mesh.CombineMeshes(combine, true, false);
return mesh;
}

Хотя есть ещё один момент. До сих пор многие из вершин в наших моделях дублировались, хотя, как вы возможно слышали, при создании моделей наоборот всегда стараются сократить число вершин и треугольников. Почему же с кубом и октаэдром не так? Покажу на примере, вот код сборки октаэдра с минимально необходимым числом вершин:
Октаэдр с общими вершинами у треугольников
public static Mesh Octahedron(float radius)
{
var v = new Vector3[6];
v[0] = new Vector3(0, -radius, 0);
v[1] = new Vector3(-radius, 0, 0);
v[2] = new Vector3(0, 0, -radius);
v[3] = new Vector3(+radius, 0, 0);
v[4] = new Vector3(0, 0, +radius);
v[5] = new Vector3(0, radius, 0);
var mesh = new Mesh
{
vertices = v,
triangles = new[] { 0, 1, 2,
0, 2, 3,
0, 3, 4,
0, 4, 1,
5, 2, 1,
5, 3, 2,
5, 4, 3,
5, 1, 4}
};
mesh.RecalculateNormals();
return mesh;
}
В конце я применил Mesh.RecalculateNormals, который автоматически считает нормали, так проще.
Посмотрите на разницу в освещении между двумя октаэдрами на соседней картинке. В первом случае шэйдеру приходится интерполировать между нормалями, смотрящими совсем в разные стороны, поэтому освещение получается нереалистичным. А во втором случае все грани острые, чёткие. Общие нормали подходят для сфер, гладких поверхностей или если необходимо скрыть малое количество полигонов. А для нашего случая вершин нужно больше.
Тетраэдр

Теперь можно взяться за фигуры поинтереснее. Расчёт вершин даже для простого тетраэдра требует потребует пятёрки по школьной геометрии, поэтому сразу предупреждаю, если не помните что на что делится в синусе, то лучше сначала заглянуть в учебник, как это пришлось сделать мне.
Освежили память? Продолжим.
Пусть наш тетраэдр стоит на одной из граней, тогда противоположную вершину можно добавить сразу:
var v = new Vector3[4];
v[0] = new Vector3(0, 1, 0);
Остальные вершины должны образовывать равносторонний треугольник. Их координаты можно найти с помощью синусов и косинусов. В Unity есть функции Mathf.Sin и Mathf.Cos, которые ведут расчёт в радианах. Делим окружность на три части и находим на ней три точки:
var segmentAngle = Mathf.PI * 2 / 3;
var currentAngle = 0f;
for (var i = 1; i <= 3; i++)
{
v[i] = new Vector3(Mathf.Sin(currentAngle), 0, Mathf.Cos(currentAngle));
currentAngle += segmentAngle;
}
Из этих вершин уже можно собрать пирамидку, но это не будет тетраэдром, потому что у настоящего тетраэдра все грани одинаковые. Для настоящего тетраэдра основание пирамиды нужно немного уменьшить и сдвинуть ниже. Тут опять пригодятся синусы и косинусы, но чтобы ими воспользоваться, немного смухлюем и подсмотрим один угол в Википедии. «Edge central angle» это угол между радиусами описанной сферы, пересекающими вершины тетраэдра. Кхм, или что-то в этом роде, я успел запутаться пока формулировал мысль. В общем присовокупив этот угол получаем следующий код:
var tetrahedralAngle = Mathf.PI * 119.4712f / 180;
А в цикле:
v[i] = new Vector3(Mathf.Sin(currentAngle) * Mathf.Sin(tetrahedralAngle), Mathf.Cos(tetrahedralAngle), Mathf.Cos(currentAngle) * Mathf.Sin(tetrahedralAngle));
Не так уж и сложно, надеюсь, что все всё поняли. Вот так выглядит всё в итоге, с добавлением масштабирования:
Тетраэдр посложнее
public static Mesh Tetrahedron(float radius)
{
var tetrahedralAngle = Mathf.PI * 109.4712f / 180;
var segmentAngle = Mathf.PI * 2 / 3;
var currentAngle = 0f;
var v = new Vector3[4];
v[0] = new Vector3(0, radius, 0);
for (var i = 1; i <= 3; i++)
{
v[i] = new Vector3(radius * Mathf.Sin(currentAngle) * Mathf.Sin(tetrahedralAngle),
radius * Mathf.Cos(tetrahedralAngle),
radius * Mathf.Cos(currentAngle) * Mathf.Sin(tetrahedralAngle));
currentAngle = currentAngle + segmentAngle;
}
var combine = new CombineInstance[4];
combine[0].mesh = Triangle(v[0], v[1], v[2]);
combine[1].mesh = Triangle(v[1], v[3], v[2]);
combine[2].mesh = Triangle(v[0], v[2], v[3]);
combine[3].mesh = Triangle(v[0], v[3], v[1]);
var mesh = new Mesh();
mesh.CombineMeshes(combine, true, false);
return mesh;
}
А вот тот же тетраэдр без математики, с захардкоденными вершинами, почувствуйте разницу:
Тетраэдр попроще
public static Mesh Tetrahedron(float radius)
{
var v0 = new Vector3(0, radius, 0);
var v1 = new Vector3(0, -radius * 0.333f, radius * 0.943f);
var v2 = new Vector3(radius * 0.816f, -radius * 0.333f, -radius * 0.471f);
var v3 = new Vector3(-radius * 0.816f, -radius * 0.333f, -radius * 0.471f);
var combine = new CombineInstance[4];
combine[0].mesh = Triangle(v0, v1, v2);
combine[1].mesh = Triangle(v1, v3, v2);
combine[2].mesh = Triangle(v0, v2, v3);
combine[3].mesh = Triangle(v0, v3, v1);
var mesh = new Mesh();
mesh.CombineMeshes(combine, true, false);
return mesh;
}
Икосаэдр

Напоследок самое вкусное — икосаэдр. Если выровнять икосаэдр и посмотреть на него под правильным углом, то можно заметить, что две его вершины лежат на одной оси друг под другом, а остальные расположены на двух окружностях.
На каждой окружности их по пять штук, а значит интервал между ними 72 градуса. Смещение между окружностями — 36 градусов. Для выравнивания вершин нам опять понадобится волшебный угол из Википедии: «If two vertices are taken to be at the north and south poles (latitude ±90°), then the other ten vertices are at latitude ±arctan(1/2) ≈ ±26.57°». В переводе на русский это означает, что волшебный угол — арктангенс одной второй.
В конечном итоге всё похоже на тетраэдр, просто окружностей две и немного сложнее сцепка вершин. Сразу добавляем две вершины, считаем одну половинку, затем другую. Собираем в треугольники четырьмя порциями.
Икосаэдр
public static Mesh Icosahedron(float radius)
{
var magicAngle = Mathf.PI * 26.565f/180;
var segmentAngle = Mathf.PI * 72 / 180;
var currentAngle = 0f;
var v = new Vector3[12];
v[0] = new Vector3(0, radius, 0);
v[11] = new Vector3(0, -radius, 0);
for (var i=1; i<6; i++)
{
v[i] = new Vector3(radius * Mathf.Sin(currentAngle) * Mathf.Cos(magicAngle),
radius * Mathf.Sin(magicAngle),
radius * Mathf.Cos(currentAngle) * Mathf.Cos(magicAngle));
currentAngle += segmentAngle;
}
currentAngle = Mathf.PI*36/180;
for (var i=6; i<11; i++)
{
v[i] = new Vector3(radius * Mathf.Sin(currentAngle) * Mathf.Cos(-magicAngle),
radius * Mathf.Sin(-magicAngle),
radius * Mathf.Cos(currentAngle) * Mathf.Cos(-magicAngle));
currentAngle += segmentAngle;
}
var combine = new CombineInstance[20];
combine[0].mesh = Triangle(v[0], v[1], v[2]);
combine[1].mesh = Triangle(v[0], v[2], v[3]);
combine[2].mesh = Triangle(v[0], v[3], v[4]);
combine[3].mesh = Triangle(v[0], v[4], v[5]);
combine[4].mesh = Triangle(v[0], v[5], v[1]);
combine[5].mesh = Triangle(v[11], v[7], v[6]);
combine[6].mesh = Triangle(v[11], v[8], v[7]);
combine[7].mesh = Triangle(v[11], v[9], v[8]);
combine[8].mesh = Triangle(v[11], v[10], v[9]);
combine[9].mesh = Triangle(v[11], v[6], v[10]);
combine[10].mesh = Triangle(v[2], v[1], v[6]);
combine[11].mesh = Triangle(v[3], v[2], v[7]);
combine[12].mesh = Triangle(v[4], v[3], v[8]);
combine[13].mesh = Triangle(v[5], v[4], v[9]);
combine[14].mesh = Triangle(v[1], v[5], v[10]);
combine[15].mesh = Triangle(v[6], v[7], v[2]);
combine[16].mesh = Triangle(v[7], v[8], v[3]);
combine[17].mesh = Triangle(v[8], v[9], v[4]);
combine[18].mesh = Triangle(v[9], v[10], v[5]);
combine[19].mesh = Triangle(v[10], v[6], v[1]);
var mesh = new Mesh();
mesh.CombineMeshes(combine, true, false);
return mesh;
}
Заключение
Если вы внимательно читали код в статье, то наверняка заметили, что там много ненужных вычислений, тот же Mathf.Cos(magicAngle) из примера выше. При желании его можно посчитать только один раз и занести в переменную, это будет не так наглядно и понятно зато быстрее.
Кроме того в генерируемых моделях не самые удобные uv-карты, было бы неплохо их исправить, но для этого придётся переделывать очень много кода, пока и так сойдёт.
А где же сферы и цилиндры? – спросите вы. Редактор статей на Хабрахабре, конечно, замечательный, но навигация по большим объёмам текста в нём не очень удобная, так что оставлю сферы на следующий раз.
Исходники и бинарники для разных платформ можете скачать по ссылкам ниже.
Unity Web Player | Windows | Linux | Mac | Исходники на GitHub
