Одним субботним декабрьским вечером сидел я над книгой The Blind Watchmaker (Слепой Часовщик), как на глаза мне попался невероятно интересный эксперимент: возьмём любое предложение, например Шекспировскую строку: Methinks it is like a weasel и случайную строку такой же длины: wdltmnlt dtjbkwirzrezlmqco p и начнем вносить в неё случайные изменения. Через сколько поколений эта случайная строка превратится в Шекспировскую строку, если выживать будут лишь потомки более похожие на Шекспировскую?
Сегодня мы повторим этот эксперимент, но в уже совершенно другом масштабе.

Структура статьи:
Осторожно трафик!
В области искусственного интеллекта под генетическим алгоритмом подразумевается эвристика поиска решений, основанная на естественном отборе. Как правило применяется для задач, где пространство поиска насколько огромно, что точное решение найти невозможно и эвристическое решение удовлетворяет требованиям. Сама задача имеет некоторую функцию качества решения, которую необходимо максимизировать.
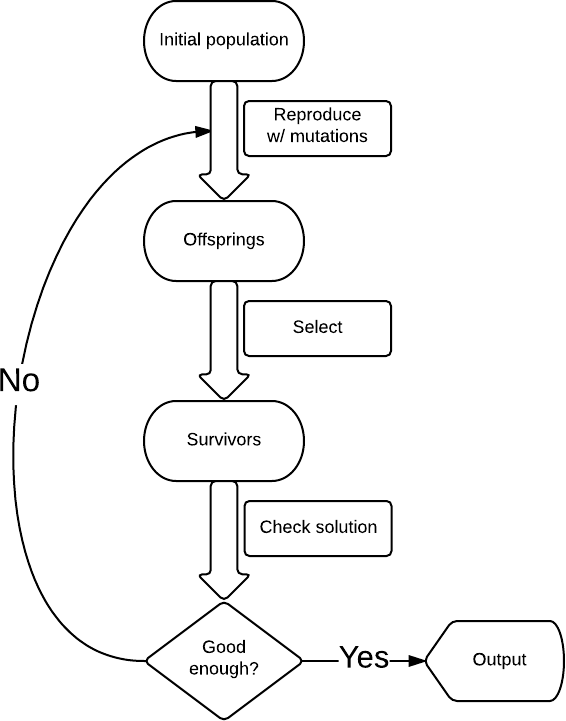
В самом простом виде генетический алгоритм имеет следующую структуру (см. схему): начинаем с некоторым решением, в нашем случае, это случайная строка; вносим мутации, например, меняем случайно выбранную букву в строке на случайно выбранную букву и получаем новый набор строк (k мутаций на строку); из них отбираем только те, которые ближе к шекспировской (по количеству совпадающих символом), например 10 таких строк, если шекспировской среди них нет, то запускаем процесс заново.
Во многом генетические алгоритмы похожи на классические методы оптимизации, популяция — это набор текущих точек, мутации — это исследование соседних точек, отбор — это выбор новых точек для поиска решения в условиях ограниченных вычислительных ресурсов.
Популяция всегда стремится к ближайшему максимуму, так как мы отбираем текущие точки поиска, как имеющие максимальное значение (все остальные точки «умрут», не выдержат конкуренции с ближайшим максимумом). Так как размер популяции значительный, а значит вероятность сделать хотя бы один шаг в направлении максимума не пренебрежимо мала, то через некоторое количество шагов популяция сместится в сторону локального максимума. А потомки точки, смещенной ближе к максимуму, имеют большую «выживаемость». Значит через достаточное количество шагов, потомки этой точки начнут доминировать в популяции и вся она сместится к максимуму.
Визуализация популяции стремящейся к локальному максимуму:
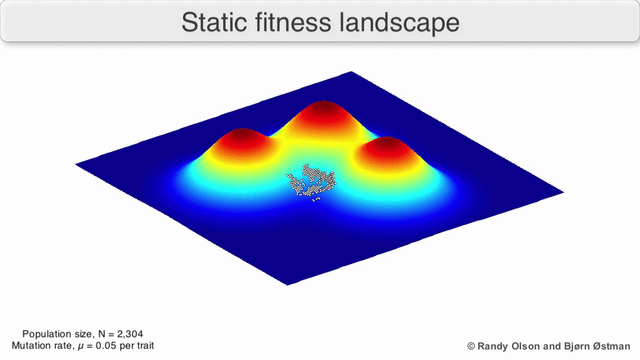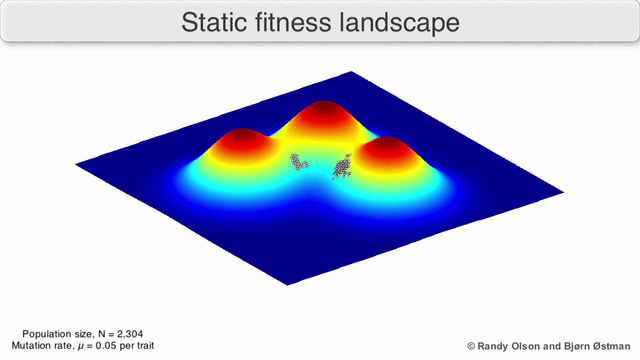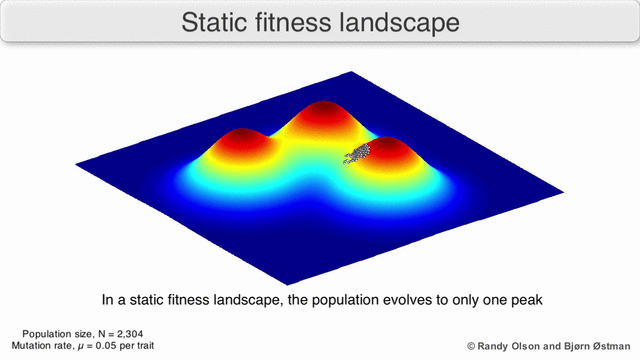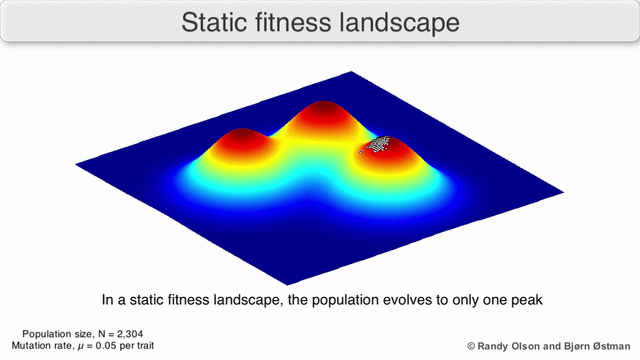
(due to Randy Olson)
Входные данные: строка S
Выходные данные: натуральное число N, равное количеству поколений необходимых для преобразования случайной строки длины len(S) в строку S
Что в нашем случае мутация? Под мутацией строки S мы понимаем замену одного случайно выбранного символа из строки S на другой произвольный символ алфавита. В данной задаче мы используем только символы нижнего регистра латиницы и пробел.
Что такое изначальная популяция (initial population в схеме)? Это случайная строка равная по длине входной строке S.
Что такое потомки (offsprings)? Пусть мы зафиксировали количество мутаций одной строки на константу k, тогда потомки — это k мутаций каждой строки текущего поколения.
Что такое выжившие (survivors)? Пусть мы зафиксировали размер популяции на константу h, тогда выжившие — это h строк максимально похожих на входную строку S.
В псевдокоде (подозрительно похожем на python) это выглядит следующим образом:

Рассмотрим следующую строку: The quick brown fox jumps over the lazy dog и воспроизведём для неё вывод нашей программы:
Рассмотрим цепочку изменений (слева номер поколения):
Как мы видим каждое поколение отличается не более, чем на один символ друг от друга. Всего потребовалось 46 поколений, чтобы добраться от rbbzmffwfhwtxnjjiozz ujhhlxeoyhezarquvmopyk до the quick brown fox jumps over the lazy dog с помощью мутаций и отбора.
Отдельные примеры, шекспировской строка или английская панграмма про лису, интересны, но не слишком убедительны. Поэтому и решил рассмотреть более интересный вопрос: что будет если взять пару классических произведений, разбить их на предложения и посчитать число поколений для каждого из них? Какой будет характер зависимости количества поколений от строки (например, от её длины)?
В качестве классических произведений выбрал To Kill a Mocking Bird by Harper Lee (Убить Пересмешника, Харпер Ли) и Catcher in the Rye by J.D. Salinger (Над Пропастью во Ржи, Джей Ди Сэлинджер). Мы будем измерять два параметра — распределение количества поколений по предложениям и зависимость количества поколений от длины строки (есть ли корреляция?).
Параметры были следующие: количество потомков у строки: 100; количество выживших в поколении: 10.
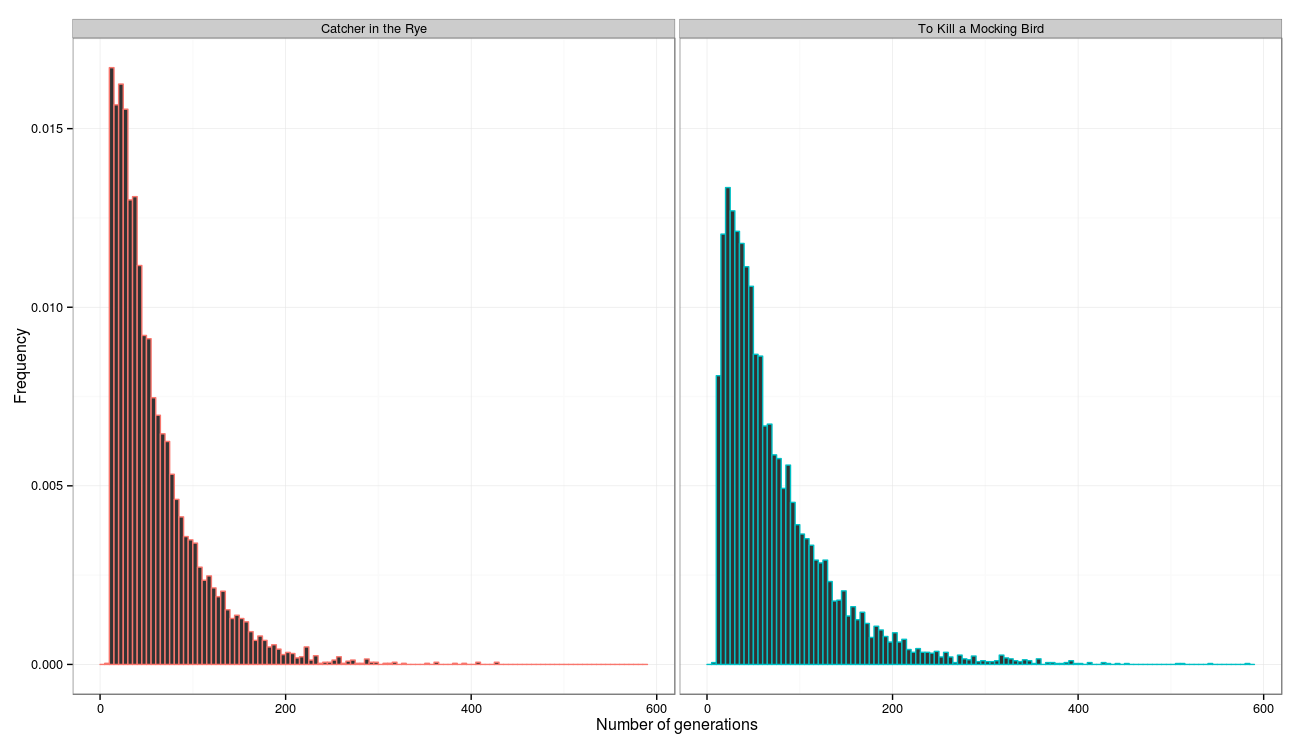
Как мы видим, для большинства предложений получилось достичь строку достаточно быстро, требуются менее 100 итераций, практически для всех предложений достаточно 200 итераций (среди всех предложений было только одно, которому потребовалось 1135 итераций, судя по предложению алгоритм разбивки ошибся и склеил несколько предложений в одно):
Корреляция между длиной строки и количеством поколений идеальная. Это означает, что практически в каждом поколении удавалось продвинуться на шаг ближе к целевой строке.
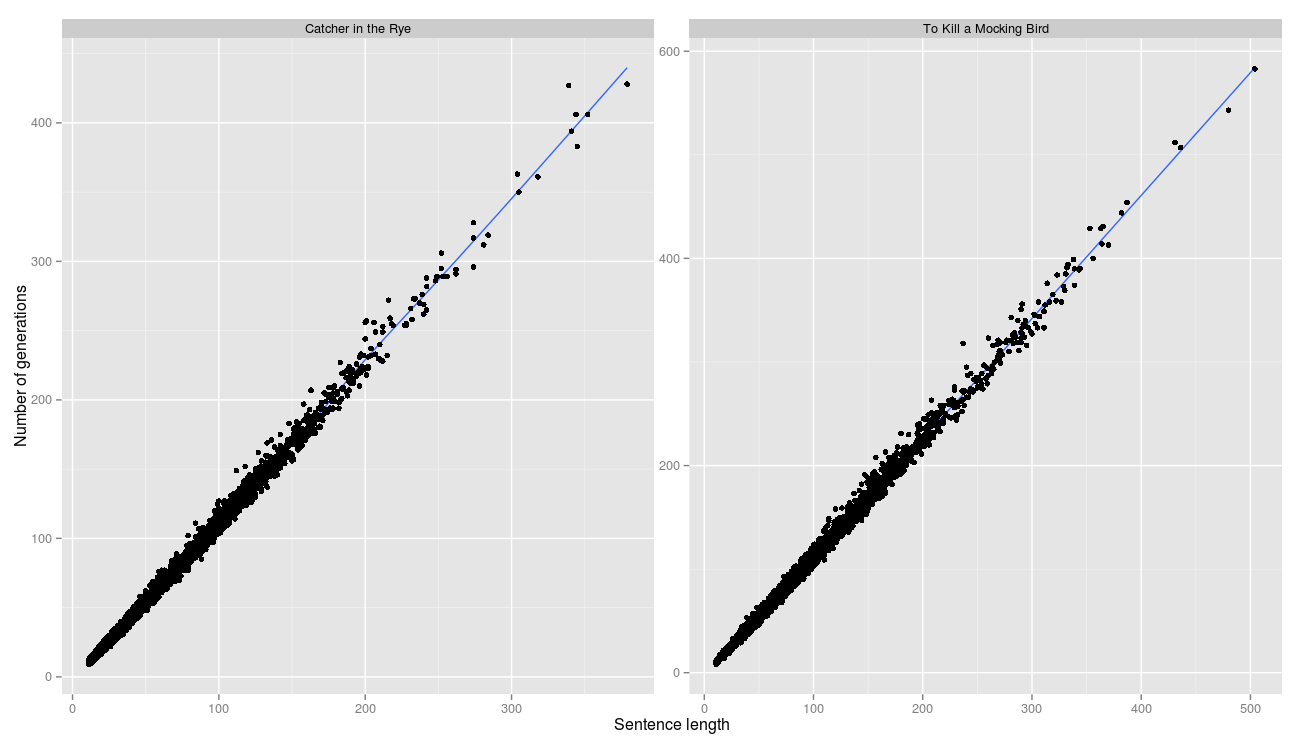
R^2 равен 0.996 и 0.997 соответственно.
Таким образом экспериментально установили, что в условиях нашей задачи для любой входной строки S, количество поколений линейно зависит от длины строки, что согласуется с исходными предположениями.
Весь код, python — генетический алгоритм\обработка текста и R — визуализация, доступен в github:
github.com/SergeyParamonov/genetics-experiments
Мы разобрались с базовой структурой генетических алгоритмов и применили для решения задачи о мутации строки. В результате экспериментов с классическими текстами мы обнаружили, что в наших условиях существуют линейная зависимость между длиной строки и количеством поколений необходимых для достижения входной строки.
Так же мы отметили, что базовая структура поиска может быть модифицирована (например, с помощью сrossover — использования несколько членов поколения для создания потомков) для решения широкого класса задач оптимизации, где слишком сложно искать точное решение.
Сегодня мы повторим этот эксперимент, но в уже совершенно другом масштабе.

Структура статьи:
- Что такое генетический алгоритм
- Почему это работает
- Формализуем задачу со случайной строкой
- Пример работы алгоритма
- Эксперименты с классикой
- Код и данные
- Выводы
Осторожно трафик!
Что такое генетический алгоритм
В области искусственного интеллекта под генетическим алгоритмом подразумевается эвристика поиска решений, основанная на естественном отборе. Как правило применяется для задач, где пространство поиска насколько огромно, что точное решение найти невозможно и эвристическое решение удовлетворяет требованиям. Сама задача имеет некоторую функцию качества решения, которую необходимо максимизировать.
В самом простом виде генетический алгоритм имеет следующую структуру (см. схему): начинаем с некоторым решением, в нашем случае, это случайная строка; вносим мутации, например, меняем случайно выбранную букву в строке на случайно выбранную букву и получаем новый набор строк (k мутаций на строку); из них отбираем только те, которые ближе к шекспировской (по количеству совпадающих символом), например 10 таких строк, если шекспировской среди них нет, то запускаем процесс заново.
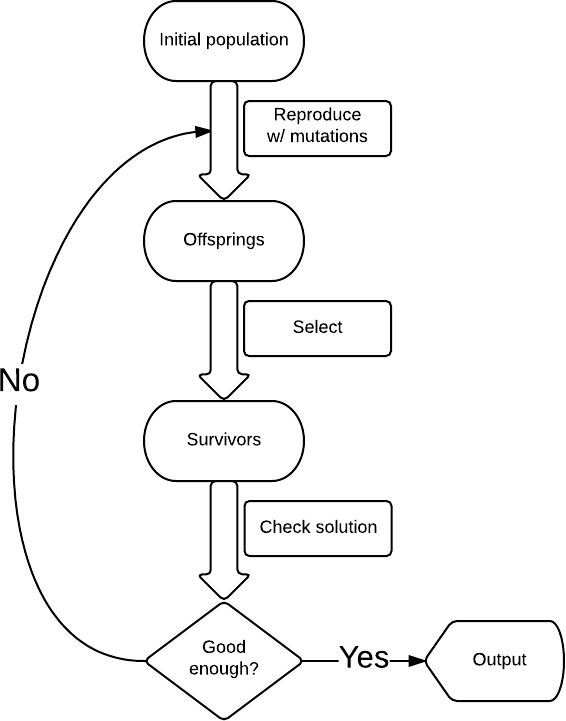
Почему это работает
Во многом генетические алгоритмы похожи на классические методы оптимизации, популяция — это набор текущих точек, мутации — это исследование соседних точек, отбор — это выбор новых точек для поиска решения в условиях ограниченных вычислительных ресурсов.
Популяция всегда стремится к ближайшему максимуму, так как мы отбираем текущие точки поиска, как имеющие максимальное значение (все остальные точки «умрут», не выдержат конкуренции с ближайшим максимумом). Так как размер популяции значительный, а значит вероятность сделать хотя бы один шаг в направлении максимума не пренебрежимо мала, то через некоторое количество шагов популяция сместится в сторону локального максимума. А потомки точки, смещенной ближе к максимуму, имеют большую «выживаемость». Значит через достаточное количество шагов, потомки этой точки начнут доминировать в популяции и вся она сместится к максимуму.
Визуализация популяции стремящейся к локальному максимуму:

(due to Randy Olson)
Формализуем задачу со случайной строкой
Входные данные: строка S
Выходные данные: натуральное число N, равное количеству поколений необходимых для преобразования случайной строки длины len(S) в строку S
Что в нашем случае мутация? Под мутацией строки S мы понимаем замену одного случайно выбранного символа из строки S на другой произвольный символ алфавита. В данной задаче мы используем только символы нижнего регистра латиницы и пробел.
Что такое изначальная популяция (initial population в схеме)? Это случайная строка равная по длине входной строке S.
Что такое потомки (offsprings)? Пусть мы зафиксировали количество мутаций одной строки на константу k, тогда потомки — это k мутаций каждой строки текущего поколения.
Что такое выжившие (survivors)? Пусть мы зафиксировали размер популяции на константу h, тогда выжившие — это h строк максимально похожих на входную строку S.
В псевдокоде (подозрительно похожем на python) это выглядит следующим образом:

Пример работы алгоритма
Рассмотрим следующую строку: The quick brown fox jumps over the lazy dog и воспроизведём для неё вывод нашей программы:
Рассмотрим цепочку изменений (слева номер поколения):
1 rbbzmffwfhwtxnjjiozz ujhhlxeoyhezarquvmopyk 2 rbbzmffwfhwtxnjjiozz ujhhlxeoyhezarquzmopyk 3 rbb mffwfhwtxnjjiozz ujhhlxeoyhezarquzmopyk 4 rbb mffwfhwtxnjjiozz ujhhlxeoyhezarquzmodyk 5 rbb mffwfhbtxnjjiozz ujhhlxeoyhezarquzmodyk 6 rbb mffcfhbtxnjjiozz ujhhlxeoyhezarquzmodyk 7 rbb mffcf btxnjjiozz ujhhlxeoyhezarquzmodyk 8 rbb mffcf btxnjjiozz ujhhlxeoyheza quzmodyk 9 rbb mffcf brxnjjiozz ujhhlxeoyheza quzmodyk 10 rbb mffcf brxnjjiozz ujphlxeoyheza quzmodyk 20 rbb mffcf bronj fox jujpslxveyheza luzmodyk 30 rbb mficf bronj fox jumps overhehe luzy dyg 40 he m ick bronn fox jumps over the lazy dog 41 he q ick bronn fox jumps over the lazy dog 42 he q ick bronn fox jumps over the lazy dog 43 he q ick brown fox jumps over the lazy dog 44 he quick brown fox jumps over the lazy dog 45 ahe quick brown fox jumps over the lazy dog 46 the quick brown fox jumps over the lazy dog
Полный вывод
print_genes("The quick brown fox jumps over the lazy dog")
1 rbbzmffwfhwtxnjjiozz ujhhlxeoyhezarquvmopyk
2 rbbzmffwfhwtxnjjiozz ujhhlxeoyhezarquzmopyk
3 rbb mffwfhwtxnjjiozz ujhhlxeoyhezarquzmopyk
4 rbb mffwfhwtxnjjiozz ujhhlxeoyhezarquzmodyk
5 rbb mffwfhbtxnjjiozz ujhhlxeoyhezarquzmodyk
6 rbb mffcfhbtxnjjiozz ujhhlxeoyhezarquzmodyk
7 rbb mffcf btxnjjiozz ujhhlxeoyhezarquzmodyk
8 rbb mffcf btxnjjiozz ujhhlxeoyheza quzmodyk
9 rbb mffcf brxnjjiozz ujhhlxeoyheza quzmodyk
10 rbb mffcf brxnjjiozz ujphlxeoyheza quzmodyk
11 rbb mffcf brxnj iozz ujphlxeoyheza quzmodyk
12 rbb mffcf brxnj ioz ujphlxeoyheza quzmodyk
13 rbb mffcf bronj ioz ujphlxeoyheza quzmodyk
14 rbb mffcf bronj ioz ujphlxeeyheza quzmodyk
15 rbb mffcf bronj ioz ujphlxeeyheza luzmodyk
16 rbb mffcf bronj ioz ujphlxveyheza luzmodyk
17 rbb mffcf bronj foz ujphlxveyheza luzmodyk
18 rbb mffcf bronj foz jujphlxveyheza luzmodyk
19 rbb mffcf bronj foz jujpslxveyheza luzmodyk
20 rbb mffcf bronj fox jujpslxveyheza luzmodyk
21 rbb mffcf bronj fox jujpslxveyheza luzm dyk
22 rbb mffcf bronj fox jujpslxverheza luzm dyk
23 rbb mffcf bronj fox jumpslxverheza luzm dyk
24 rbb mffcf bronj fox jumpslxverheha luzm dyk
25 rbb mffcf bronj fox jumpslxverhehe luzm dyk
26 rbb mffcf bronj fox jumps xverhehe luzm dyk
27 rbb mffcf bronj fox jumps xverhehe luzm dyg
28 rbb mffcf bronj fox jumps xverhehe luzy dyg
29 rbb mffcf bronj fox jumps overhehe luzy dyg
30 rbb mficf bronj fox jumps overhehe luzy dyg
31 rbb mficf bronj fox jumps overhehe lazy dyg
32 rbb mficf bronn fox jumps overhehe lazy dyg
33 rbb mficf bronn fox jumps over ehe lazy dyg
34 rhb mficf bronn fox jumps over ehe lazy dyg
35 hb mficf bronn fox jumps over ehe lazy dyg
36 hb mfick bronn fox jumps over ehe lazy dyg
37 hb m ick bronn fox jumps over ehe lazy dyg
38 hb m ick bronn fox jumps over ehe lazy dog
39 he m ick bronn fox jumps over ehe lazy dog
40 he m ick bronn fox jumps over the lazy dog
41 he q ick bronn fox jumps over the lazy dog
42 he q ick bronn fox jumps over the lazy dog
43 he q ick brown fox jumps over the lazy dog
44 he quick brown fox jumps over the lazy dog
45 ahe quick brown fox jumps over the lazy dog
46 the quick brown fox jumps over the lazy dog
Как мы видим каждое поколение отличается не более, чем на один символ друг от друга. Всего потребовалось 46 поколений, чтобы добраться от rbbzmffwfhwtxnjjiozz ujhhlxeoyhezarquvmopyk до the quick brown fox jumps over the lazy dog с помощью мутаций и отбора.
Эксперименты с классикой
Отдельные примеры, шекспировской строка или английская панграмма про лису, интересны, но не слишком убедительны. Поэтому и решил рассмотреть более интересный вопрос: что будет если взять пару классических произведений, разбить их на предложения и посчитать число поколений для каждого из них? Какой будет характер зависимости количества поколений от строки (например, от её длины)?
В качестве классических произведений выбрал To Kill a Mocking Bird by Harper Lee (Убить Пересмешника, Харпер Ли) и Catcher in the Rye by J.D. Salinger (Над Пропастью во Ржи, Джей Ди Сэлинджер). Мы будем измерять два параметра — распределение количества поколений по предложениям и зависимость количества поколений от длины строки (есть ли корреляция?).
Параметры были следующие: количество потомков у строки: 100; количество выживших в поколении: 10.
Результаты
Как мы видим, для большинства предложений получилось достичь строку достаточно быстро, требуются менее 100 итераций, практически для всех предложений достаточно 200 итераций (среди всех предложений было только одно, которому потребовалось 1135 итераций, судя по предложению алгоритм разбивки ошибся и склеил несколько предложений в одно):

Корреляция между длиной строки и количеством поколений идеальная. Это означает, что практически в каждом поколении удавалось продвинуться на шаг ближе к целевой строке.
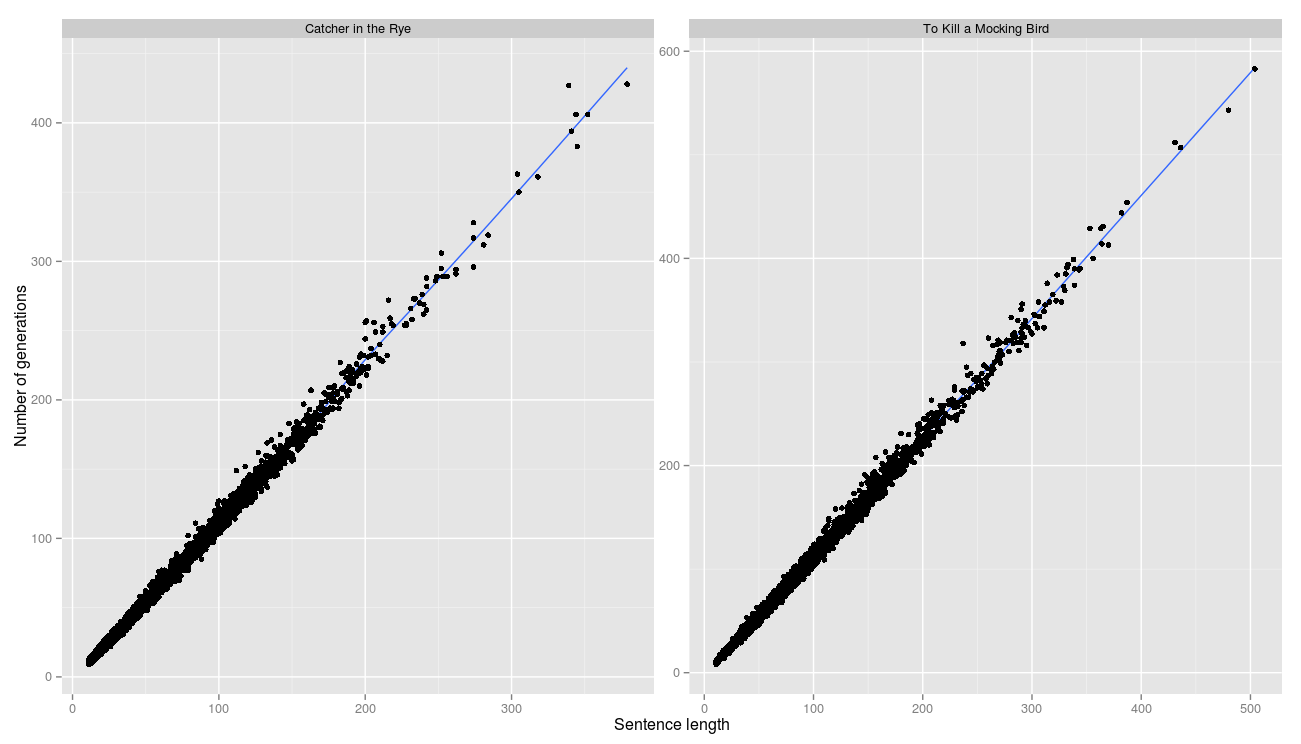
R^2 равен 0.996 и 0.997 соответственно.
Таким образом экспериментально установили, что в условиях нашей задачи для любой входной строки S, количество поколений линейно зависит от длины строки, что согласуется с исходными предположениями.
Код и данные
Весь код, python — генетический алгоритм\обработка текста и R — визуализация, доступен в github:
github.com/SergeyParamonov/genetics-experiments
Выводы
Мы разобрались с базовой структурой генетических алгоритмов и применили для решения задачи о мутации строки. В результате экспериментов с классическими текстами мы обнаружили, что в наших условиях существуют линейная зависимость между длиной строки и количеством поколений необходимых для достижения входной строки.
Так же мы отметили, что базовая структура поиска может быть модифицирована (например, с помощью сrossover — использования несколько членов поколения для создания потомков) для решения широкого класса задач оптимизации, где слишком сложно искать точное решение.








