Естественные паттерны
Системы Линденмайера придумал венгерский биолог Аристид Линденмайер, изучая рост водорослей. Он разработал L-системы как способ описания процесса роста водорослей и простых растений. Результатом стал своего рода язык, на котором можно было выразить свойства рекурсивности и самоподобия роста организма. И в самом деле, L-системы можно использовать для генерирования естественных паттернов; кроме того, хорошо известные математические паттерны тоже можно записать в виде L-системы. В этой статье я расскажу о различных типах L-систем и продемонстрирую их с помощью отрисовки «черепашьей графикой» двухмерных и трёхмерных систем Линденмейера.
Язык очень прост, он состоит из символов (алфавита) и продукционных правил. Первое состояние предложения называется аксиомой. К этой аксиоме можно многократно применить продукционные правила для эволюции или роста системы. В качестве простого примера можно взять систему с аксиомой
и правилом 
. После первой итерации (первого случая применения правила) предложение сменится на 
. После второй итерации предложение будет иметь вид 
, и так далее. Можно увидеть, как саморасширяющееся предложение становится аналогом деления клеток в растениях и других биологических процессов.| [A...Z] | Любая (не являющаяся константой) буква алфавита перемещает черепашку вперёд на фиксированное расстояние |
| + | Поворот черепашки вправо на фиксированное число градусов |
| - | Поворот черепашки влево на фиксированное количество градусов |
| [ | Запись текущего состояния черепашки в стек |
| ] | Извлечение последнего состояния черепашки из стека и присвоение этого состояния |
Отрисовка предложений
После того, как система задана и все итерации выполнены, у нас получается большое предложение с интересными свойствами. Для визуализации этих свойств нам необходимо создать способ их рендеринга. В этой статье я буду рендерить систему при помощи «черепашьей графики».
Черепашья графика рендерится размещением на декартовой плоскости «черепашки» и передачей ей инструкций. Черепашка движется в соответствии с полученными ею инструкциями. Черепашка выполняет рисование, оставляя за собой след. В нашем случае черепашке отправляется каждый символ из предложения L-системы. В представленном выше коротком примере предложение достаточно просто, в нём содержатся только буквы. Сложно преобразовать строку букв в интересные инструкции для черепашки. Поэтому для кодирования команд черепашке задаются специальные символы. На Рисунке 1 показан ключ к моему черепашьему языку.
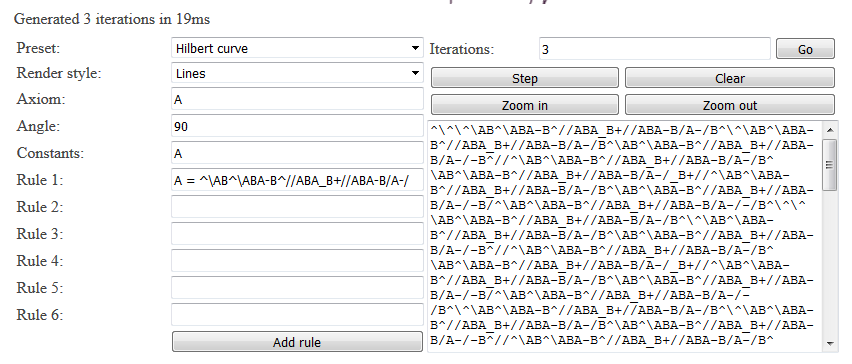
Ниже я реализовал интерактивный (в оригинале статьи) рендерер 2D-систем Линденмайера. В нём есть несколько примеров, а также можно задавать собственные системы из шести продукционных правил. Я добавил поле constants, в котором содержится строка символов. При рендеринге строки черепашкой она будет игнорировать все символы, являющиеся константами. Тем не менее, символы-константы всё равно подвержены действию правил. В поле angle указано количество градусов, на которые поворачивается черепашка при командах
+ и -. В полях правил можно использовать константу AXIOM. Она будет заменяться на исходную аксиому. Это используется в нескольких примерах.Примеры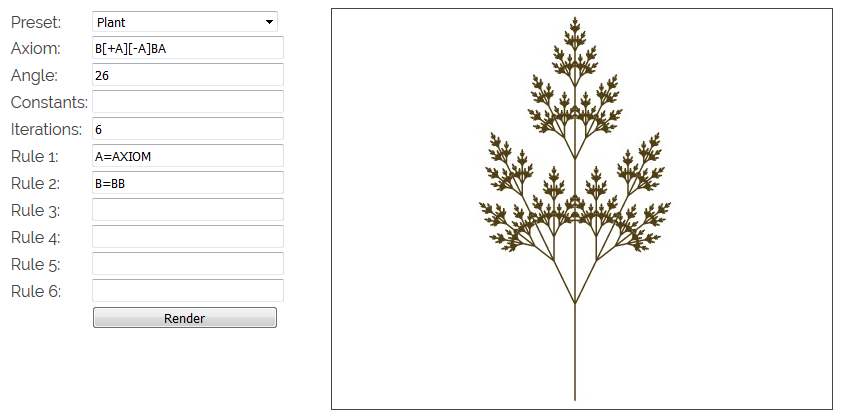
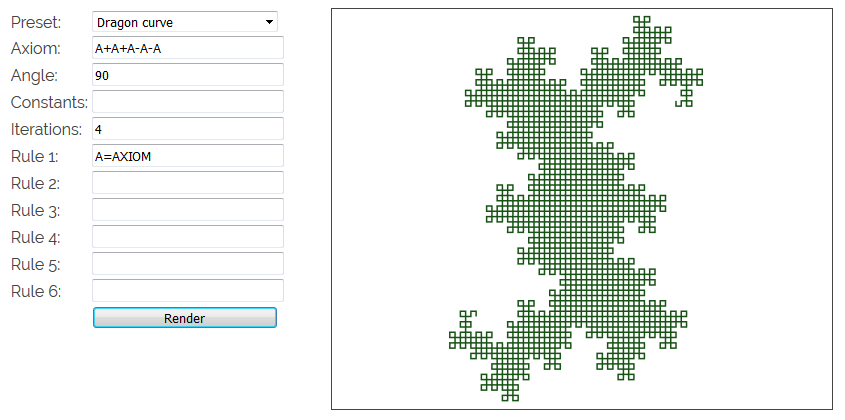
Исходный код этого примера на javascript находится в репозитории. Показанные примеры систем демонстрируют некоторые из возможностей систем Линденмайера, от шумных, похожих на случайные паттерны до строгих геометрических узоров. Все системы демонстрируют свойство самоподобия; когда количество итераций становится высоким, мелкие создаваемые детали уже неразличимы. Однако в теории мы можем неограниченно уменьшать масштаб, повышая при этом точность. Это хорошо известное свойство фракталов. При уменьшении масштаба фракталов часто видны те же паттерны, что и при большем масштабе.
Добавляем размерности
Показанный выше пример может полностью демонстрировать свойства систем Линденмайера, но я хочу добавить ещё несколько характеристик, чтобы сделать алгоритм ещё мощнее. Лично меня очень интересует использование 3D-систем Линденмайера для генерирования растений и природных систем. Очень интересный источник информации по этой теме — веб-сайт группы по исследованию биологического моделирования и визуализации Университета Калгари. По этой тематике существует множество статей, которые представлены на этом веб-сайте.
Я хочу оставить мою систему как можно более простой, но мне не хватает некоторых особенностей, которые необходимы для создания более сложных систем. Я хотел бы по крайней мере моделировать следующее:
- Должна присутствовать возможность какой-нибудь рандомизации, потому что мы считаем, что в природе существует случайность форм
- Я хочу, чтобы символы могли отслеживать свой возраст, потому что в природе поведение клеток может зависеть от их возраста
- Продукционные правила должны учитывать контекст символов
- Я хочу отслеживать расстояние до корневой клетки
- Черепашка должна уметь двигаться в трёх измерениях, что позволит создавать более сложные формы
Реализовать движение в трёх измерениях не так сложно. Вместо перемещения на декартовой плоскости черепашка будет позицией в кватернионе. На каждом шаге я буду прибавлять единичный вектор (направленный вверх), повёрнутый этим кватернионом в положение черепашки, а сам кватернион будет поворачиваться при встрече символов поворота. Моделирование других особенностей как можно более простым способом будет немного более хитрой задачей.
| [A...Z] | Любая (не являющаяся константой) буква алфавита перемещает черепашку вперёд на фиксированное расстояние |
| + | Рыскание черепашки вправо на фиксированный угол |
| - | Рыскание черепашки влево на фиксированный угол |
| / | Крен черепашки вправо на фиксированный угол |
| \ | Крен черепашки влево на фиксированный угол |
| ^ | Тангаж черепашки вверх на фиксированный угол |
| _ | Тангаж черепашки вниз на фиксированный угол |
| [ | Запись текущего состояния черепашки в стек |
| ] | Извлечение последнего состояния черепашки из стека и его присвоение |
Параметрическая грамматика
Чтобы упростить новые характеристики, мне нужно расширить алфавит и синтаксис. На Рисунке 2 показан ключ этой новой системы. Новые символы таблицы — это символы поворота, необходимые для перемещения черепашки в 3D-пространстве.
Случайность легко моделировать добавлением одному символу множества нечётких продукционных правил. Если у символа есть несколько правил, то случайным образом выбирается одно из них.
Для моделирования возраста клетки и расстояния до корня я мог бы добавить к каждому символу по две переменные. Если бы мне затем нужно было добавить другие свойства, то пришлось бы добавлять новые переменные. Такой подход оказался бы не особо гибким и очень специфичным. К счастью, есть более общее решение: параметрические системы Линденмайера. В параметрических L-системах за каждым символом следует список параметров (при их наличии). Продукционные правила могут быть применимы к символам с определённым набором параметров или для определённых условий этих параметров; кроме того, получаемые при использовании правила символы тоже могут иметь свои параметры.
Я продемонстрирую эту новую систему на примере символа с одним параметром (возрастом символа, измеряемым в количестве итераций). Пусть аксиомой является
, а единственным продукционным правилом — 
. При каждой итерации параметр каждого символа будет увеличиваться на единицу. Теперь я хочу изменять каждый символ на 
, когда он достигает возраста восьми итераций. Продукционное правило будет иметь вид 
. Если я задам для этой системы продукционное правило 
, то оно никогда не применится: в системе не будет символа с двумя параметрами. Стоит учесть, что 
и 
в этих примерах выбраны произвольно; они используются для работы со значениями параметров. У этих параметров нет конкретных имён, и — это просто переменные и могут быть любым символом.Я добавил в язык два синтаксических правила: в скобках за символом указывается количество параметров, разделённых запятыми, а за первым операндом продукционного правила может идти символ
, если оно должно выполняться только при соблюдении условия после этого символа. Параметрическая грамматика позволяет реализовать гораздо более обширные возможности, чем мне требовались изначально.Контекстно-зависимая грамматика
Система почти завершена. Последнее, что я хочу закодировать — это контекст. Контекст символа должен влиять на применяемые к нему правила. Теоретически, я мог бы закодировать контекст в параметрах символов, но в этом случае получится очень сложная система правил и списков параметров. Поэтому вместо этого я добавлю к продукционным методам одно последнее синтаксическое правило.
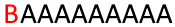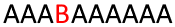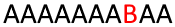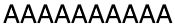
Рисунок 3: Контекстно-зависимая система Линденмайера в действии
Допустим, у меня есть аксиома, состоящая из нескольких
и одного в начале, и я хочу, чтобы перемещался на один шаг вправо на каждой итерации, не изменяя длину предложения. Это можно реализовать с помощью контекстно-зависимого правила. Во-первых, я добавлю правило 
. Его следует читать следующим образом: 
, если символу предшествует . При каждой итерации, в которой применяется это правило, каждый символ , слева от которого находится , будет меняться на . Теперь мне просто нужно, чтобы двигался, поэтому после каждой итерации снова должен становиться , чтобы все со временем не превратились в . Это реализуется простым правилом 
. На Рисунке 3 показана эта система, эволюционирующая в течение одиннадцати итераций, а начальная аксиома имеет вид 
.Эта контекстно-зависимая грамматика совместима с описанной выше параметрической грамматикой. Допустим, у меня есть предложение из нескольких вхождений
, где значение для разных символов разное. Я хочу написать контекстно-зависимое продукционное правило, которое заменяет 
на только когда окружён другими вхождениями , чьи параметры равны; иными словами, слева и справа должны быть с одинаковыми значениями параметра. Продукционное правило выглядит следующим образом:
То есть последним дополнением грамматики становятся символы
и 
. Если левому операнду продукционного правила предшествует , то в качестве контекста ему требуется символ перед . Если за ним следует , то в качестве контекста ему требуется символ после . У продукционных правил также может не быть контекста, или быть только правый/левый контекст.Трёхмерная контекстно-зависимая параметрическая система Линденмайера
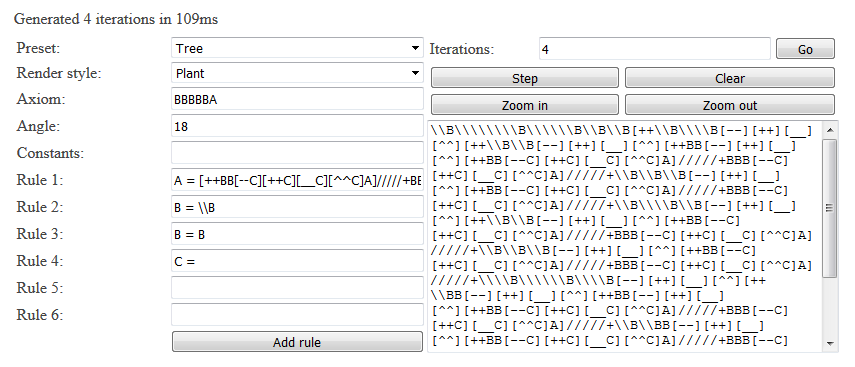
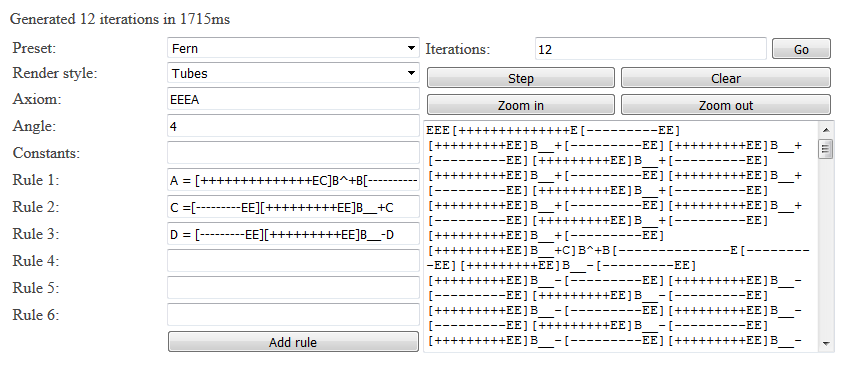
Теперь всё готово для создания рендерера трёхмерной контекстно-зависимой параметрической системы Линденмайера, которую я реализовал ниже (в оригинале статьи). В ней присутствуют все описанные в этой статье возможности. Большинство полей предыдущего 2D-рендерера скопировано, но в этой системе добавлена кнопка пошагового эволюционного изменения и функция печати конечного предложения. Парсер контекстно-зависимых параметрических систем Линденмайера находится в этом репозитории.
Реализовано несколько режимов рендеринга. Сгенерированное 3D-изображение можно поворачивать перетаскиванием мышью (или пальцем на сенсорном экране) и масштабировать колёсиком мыши. Исходный код этого рендерера находится на GitHub. Нажмите на кнопку Go, чтобы сгенерировать текущую систему.
Примеры
Вывод
Системы Линденмайера позволяют создавать очень интересные и естественные паттерны, которые могут быть полезными во многих областях. Помимо моделирования фракталов, их можно использовать для генерирования природного контента, например, деревьев и растений. Ещё одной областью применения является генерация процедурного окружения, в которой важную роль играют контекстно-зависимые правила. Я подозреваю, что системы Линденмайера можно изменять с помощью генетических алгоритмов, слегка изменяя продукционные правила. Это может оказаться очень интересным способом для эволюционного изменения растений, и я хочу поэкспериментировать с ним, если найдётся свободное время.
Похоже, что L-системы способны с определённой степенью точности моделировать природу. Любопытно, до какой степени они на самом деле могут моделировать процессы природного роста с помощью обнаруженных мною правил?
