Материал, описанный ниже, является результатом совместной работы с преподавателями ТУ Ильменау в рамках местного курсового проекта (Advanced Research Project). Опыт интересный, но и не лишенный определенных сложностей. Делали мы этот проект (и ещё один) вместе с моей тогда ещё невестой — да, так вот нам повезло и учиться вместе, и поехать на стажировку в Германию. По правде сказать, эту часть работы делала в большей степени именно она, но популяризировать эту тему хочется мне.
Итак, однажды мы назначили встречу, чтобы выбрать тему научной работы...

Короткая предыстория (в лицах)
Немецкий преподаватель №1: О, я слышал, вы там у себя изучаете спутники формата CubeSat?
Я и моя будущая супруга: Ну, можно сказать и так...
Н.п. №1: Здорово! А что если попробовать рассмотреть оптическую связь между спутниками? Я знаю, что в некоторых случаях оптика даёт лучшие показатели по энергетике, для таких маленьких спутников, я предполагаю, данный вопрос весьма важен. У меня есть один товарищ, который профессионально занимается беспроводной оптикой. Я думаю, получится интересный проект!
Мы: Звучит интересно!
(проходит некоторое время)
Встреча с Немецким преподавателем №2.
Н.п. №2: Да, всё это, конечно, здорово, но что за спутники? Такая небольшая масса? Они вообще могут коммуницировать? Кто это предложил? Понятно… Видимо, его мы на этих встречах не увидим. Отправляйтесь-ка на поиски реальных примеров — пока не верю.
И мы отправились...
И, к радости своей, нашли даже целую статью посвященную данной тематике. Важное различие заключалось в том, что связь через оптику предполагалась с Землей, а не между спутниками. Это весьма важно, потому как:
- всякого рода рассеиваний и помех, конечно, в данном случае больше,
- однако, и приёмник на Земле можно поставить достаточно крупный, и передатчик подобрать довольно-таки точный. А космический сегмент, мягко говоря, всё немного усложняет.
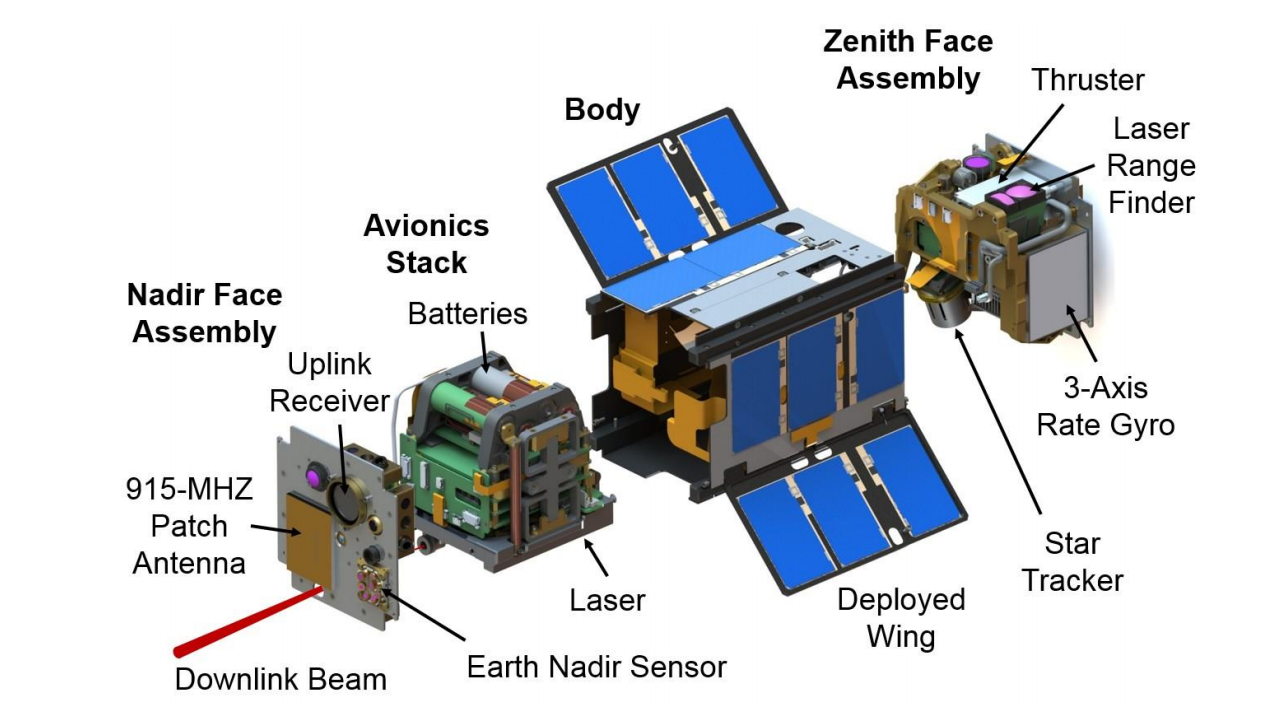
Рис. 1. Схематическое изображение наноспутника AeroCube-OCSD [1].
Но это было уже что-то, и мы снова назначили встречу.
Н.п. №2: Нуу, хорошо, раз уж НАСА… Давайте попробуем посчитать энергобюджет и сравнить его с энергобюджетом радиолинии. Статьи по тематике скинуть?
И он скинул свою статью [2] (я буду несколько раз на неё сегодня ссылаться) и ещё пару статей других авторов для общего понимания вопроса.
Что же подразумевает под собой энергобюджет межспутниковой оптической линии?
Беспроводной оптический энергобюджет
А подразумевает он под собой то же, что и обычно (необходимую мощность передатчика, принимаемую мощность, SNR и т.д.) — только шумы считаются несколько интереснее, чем в случае радиосвязи...
Начнем моделировать — будет немного понятнее:
import numpy as np
from matplotlib.pyplot import plot, grid, xlabel, ylabel, legend
import matplotlib.pyplot as plt
from scipy import specialДопустим, есть у нас такая вот система:
#initial parameters for optical case
R = 100*1e3 #distance between objects, e.g. satellites, in m (100 km)
Bit_rate = 1e6 #bit rate (1 Mbps)
h = 6.62607004*1e-34 # Planck constant
c = 299792458 #speed of light
wavelength_opt = 1550*1e-9 #optical wavelength
freq_opt = c/wavelength_opt #optical frequency
Ptx_opt = 1 #transmitter power in Watts
Ptx_opt_dBm = 10*np.log10(Ptx_opt*1e3) #transmitter power in dBmПрименительно к данной системе определим некоторое множество возможных диаметров оптических приёмников (по сути, линз) — держим в голове ограничения по размеру самих спутников:
a = [i for i in range(0,50,5)]
a = np.array(a)*1e-3 #diameter of the receiver (in meters)
a[0] = 1*1e-3
a_m = a*100 # for figures (in cm)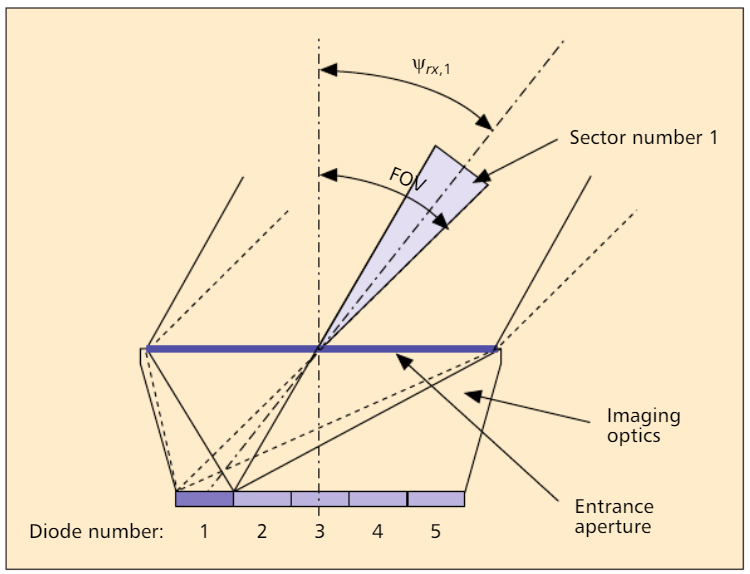
Рис.2. Принципиальная схема фотоприемника: в качестве примера показан сектор №1, углы падения которого отображаются на фотодиод №1 [2].
А также зададим некоторые возможные углы расходимости луча лазера (нашего передатчика):
div_ang = [0.2*1e-3, 0.5*1e-3, 2*1e-3, 5*1e-3, 7*1e-3]
div_ang = np.array(div_ang) #half of divergence angle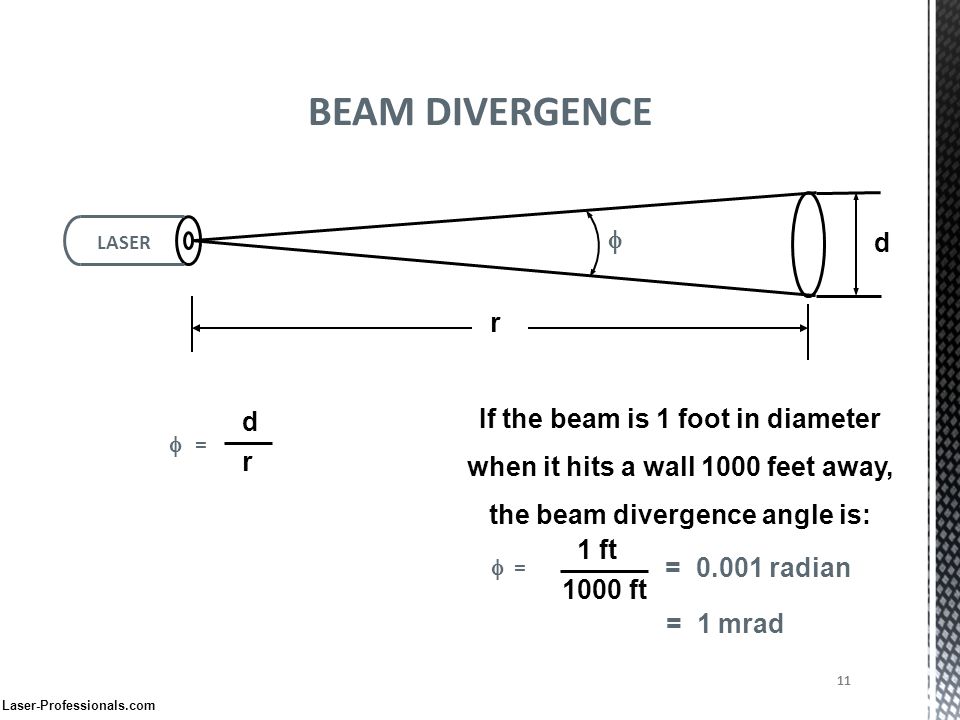
Рис. 3. Иллюстрация угла расходимости луча лазера.
Мощность на входе приёмника (received power) можно посчитать по формуле [2]:
где — это площадь приёма,
— диаметр приёмной линзы,
— расстояние между спутниками,
— это половина угла расхождения и
— передаваемая мощность.
Prx_opt_dBm = np.zeros((len(div_ang), len(a)))
Prx_opt = np.zeros((len(div_ang), len(a)))
Pathloss_dBm = np.zeros((len(div_ang), len(a)))
Pathloss = np.zeros((len(div_ang), len(a)))
Arx_m2 = (np.pi/4)*(a**2)
for f, dvangl in enumerate(div_ang):
#received power
Prx_opt[f,:] = (Ptx_opt*Arx_m2)/ (2*np.pi*(R**2))\
*(1-(np.log(2)/np.log(np.cos(dvangl))))
Prx_opt_dBm[f,:] = 10*np.log10(Prx_opt[f,:]*1e3)
#path loss
Pathloss[f,:] = (Arx_m2)/(2*np.pi*(R**2))\
*(1-(np.log(2)/np.log(np.cos(dvangl))))
Pathloss_dBm[f,:] = 10*np.log10(Pathloss[f,:]*1000)Окей, что-то уже есть. Но насколько всё это реализуемо физически?
Ограничения чувствительности
Квантовые пределы
Во-первых, вспоминаем формулу энергии фотона:
где = 6.62607004e-34
— это постоянная Планка, а
— частота несущего сигнала (Гц).
Далее последует небольшая эвристика, почерпнутая нами из консультаций. Если кто-то знает теоретическое обоснование или опровержение — пожалуйста, поделитесь!
Во-вторых, рассчитываем требуемую для детектирования энергию (минимальную энергию на один бит информации для обнаружения хоть чего-нибудь на стороне приемника):
где — среднее число фотонов, необходимое для обнаружения 1 бита информации.
Теоретическая значение энергии для оптического импульса:
E_theor = 10*h*freq_opt Более реалистичное значение энергии для оптического импульса (диод APD):
E_real_APD = 1000*h*freq_opt Более реалистичное значение энергия для оптического импульса (диод PIN):
E_real_PIN = 10000*h*freq_opt 
Рис.4. Схема рассматриваемых фотодиодов.
Требуемая (минимальная) мощность приема (максимальная чувствительность):
где — это полоса пропускания канала связи, а
— это битрейт.
P_req_theor = 10*np.log10(E_theor*Bit_rate*1000)
P_req_real_APD = 10*np.log10(E_real_APD*Bit_rate*1000)
P_req_real_PIN = 10*np.log10(E_real_PIN*Bit_rate*1000)Но и это ещё не всё: свою ограничивающую лепту ведь вносит и модуляция.
Границы, зависящие от вероятности ошибки
В качестве отправной точки будем рассматривать модуляцию OOK (On-off Keying).

Рис.5. Иллюстрация принципа OOK модуляции.
Вероятность ошибок (BER) для неё составит [2]:
где — это отношение сигнал-шум,
— это дисперсия шума (т.е. мощность шума), а
— это чувствительность фотодиодов (photodiode responsivity).
BER для OOK (PIN диод):
И следовательно:
BER для OOK (APD диод):
И поэтому:
где — это некоторое справочное усиление.
Мощность шума
Как вы могли догадаться, шумы для диодов тоже будут рассчитываться по-разному.
Мощность шума для PIN-диода
Тепловой шум можно посчитать по формуле [3, p 11]:
где ,
— постоянная Больцмана,
— прямое сопротивление,
— ёмкость фотодиода,
— заряд электрона,
— ток база-эмиттер (base-emitter или leakage или bias current),
— значение Personick integral (- сдаюсь, не нашёл адекватного перевода, прошу подсказать) для теплового шума,
— битрейт,
— спектральная плотность шума.
Cd = 2*1e-12 #capacitance of the photodiode
T = 290 #absolute temperature
Rf = 100/(Cd*2*np.pi*Bit_rate) #photodiode resistance
k = 1.38064852*1e-23 #Bolzman constant
I2 = 0.562 #depends on filter (Personick integral) for match filter
q = 1.60217662*1e-19 #electron charge
Ibe = (0.25*1e-3)/200
#RESULT
thermal_Noise_variance_add = 2*q*Ibe*I2*Bit_rate
N_0 = 4*k*T/Rf #thermal noise density for PIN
thermal_Noise_variance = N_0*Bit_rate*I2Мощность шума для APD-диода
Для этого диода приготовьтесь — много латинских букв:
где — темновой ток (dark current),
— это типичное усиление (кремний),
— коэффициент избыточного шума (the excess noise factor).
Параметры почерпнуты из следующего:
В данной работе мы не учитываем шум входного полевого транзистора (input FET noise) и шум нагрузки входного полевого транзистора (noise of the input FET load). Подробнее об этих терминах читайте в [3, p 15].
Id = 0.05*10e-9 #dark current (500e-12)
M_Si = 100 #typical gain
F_Si = 7.9 #excess noise factor
apd_noise_Si = 2*q*Id*I2*Bit_rate*(M_Si**2)*F_Si #noiseМоделирование
Принимаемая мощность
Подставим всё выясненное в наши формулы:
r = 0.53 #A/W photodiode responsivity
Pb = 10e-9 #Bit error rate (BER)
P_req_pin = 10*np.log10((special.erfcinv(2*Pb)*
np.sqrt(2*(thermal_Noise_variance+thermal_Noise_variance_add))/(r))*1e3) #in dBm
P_req_apd_lin = special.erfcinv(2*Pb)*np.sqrt(2*(thermal_Noise_variance+apd_noise_Si))/(r*M_Si)
P_req_apd = 10*np.log10(P_req_apd_lin*1e3) #in dBm
fig = plt.figure(figsize=(10, 7), dpi=300)
req_theor = np.ones((len(a_m),))*P_req_theor
req_real_APD = np.ones((len(a_m),))*P_req_real_APD
req_real_PIN = np.ones((len(a_m),))*P_req_real_PIN
PIN = np.ones((len(a_m),))*P_req_pin
APD = np.ones((len(a_m),))*P_req_apd
a_m = a_m.reshape((10,))
plot(a_m, Prx_opt_dBm[0,:],'-o', label = '0.2 mrad')
plot(a_m, Prx_opt_dBm[1,:],'-o', label = '0.5 mrad')
plot(a_m, Prx_opt_dBm[2,:],'-o', label = '2 mrad')
plot(a_m, Prx_opt_dBm[3,:],'-o', label = '5 mrad')
plot(a_m, Prx_opt_dBm[4,:],'-o', label = '7 mrad')
plot(a_m, req_theor,'k--', label = 'Sensitivity limit (theory)')
plot(a_m, req_real_APD, '--*', label = 'Sensitivity limit (APD)')
plot(a_m, req_real_PIN, '--', label = 'Sensitivity limit (PIN)')
plot(a_m, APD, '-*',label = '1e-9 OOK BER limit (APD)')
plot(a_m, PIN, label = '1e-9 OOK BER limit (PIN)')
plt.gca().invert_yaxis()
xlabel('Rx diameter (cm)'); ylabel('Prx and Preq (dBm)')
legend()
grid()
plt.show()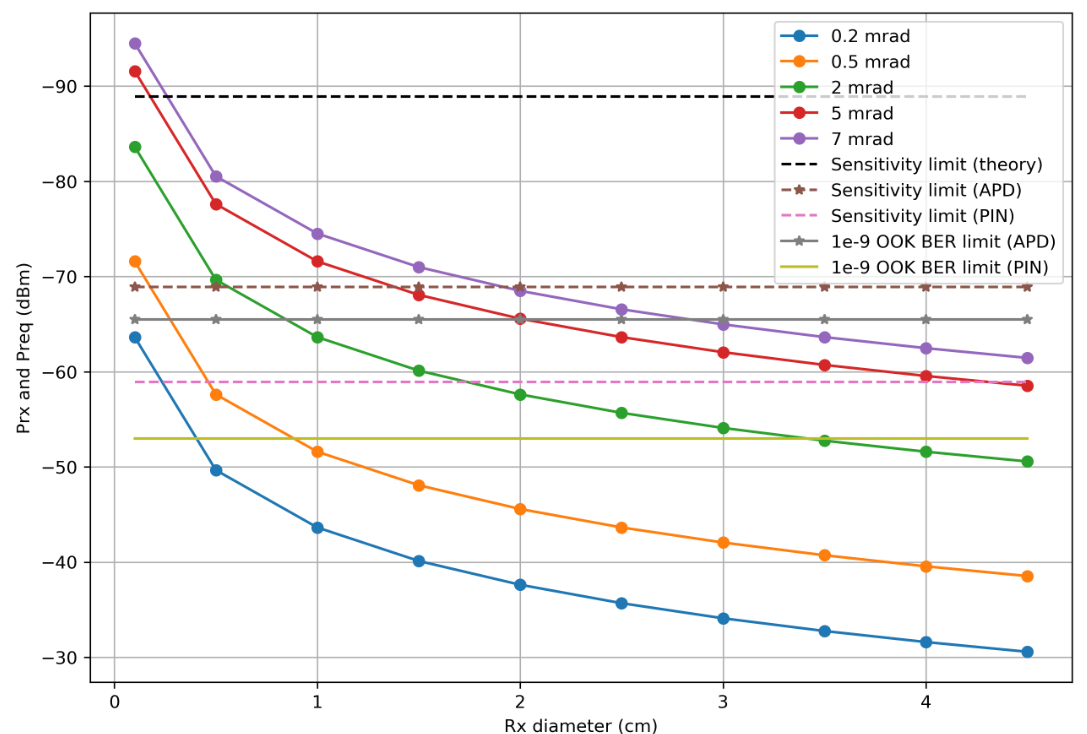
Поясним, смотреть нужно на те части кривых, которые лежат ниже соответствующих горизонтальных линий: например, для PIN-диода, OOK модуляции и угла рассеивания передатчика 2 mrad необходима линза диаметром не меньше 4 см.
Передаваемая мощность
А теперь давайте рассмотрим обратную проблему: зафиксируем некоторую мощность на приемной стороне и посмотрим какую нужно будет приложить мощность на стороне передающей:
где — это затухания на пути распространения (path loss), а
— это некоторый запас на потери (margin).
Prx_req_dB_APD = -65.5
Prx_req_dB_PIN = -52.9
margin = 5
Arx_m2 = np.zeros((len(a)))
Ptx_variable_APD = np.zeros((len(div_ang), len(a)))
Ptx_variable_PIN = np.zeros((len(div_ang), len(a)))
#area rx
Arx_m2 = (np.pi/4)*(a**2)
for f, dvangl in enumerate(div_ang):
#Ptx required
Ptx_variable_APD[f,:] = Prx_req_dB_APD + np.abs(Pathloss_dBm[f,:]) + margin;
Ptx_variable_PIN[f,:] = Prx_req_dB_PIN + np.abs(Pathloss_dBm[f,:]) + margin;
fig = plt.figure(figsize=(10, 7), dpi=300)
plot(a_m, Ptx_variable_APD[0,:],'-o', label = 'APD, 0.2 mrad')
plot(a_m, Ptx_variable_PIN[0,:],'-*', label = 'PIN, 0.2 mrad')
plot(a_m, Ptx_variable_APD[1,:],'-o', label = 'APD, 0.5 mrad')
plot(a_m, Ptx_variable_PIN[1,:],'-*', label = 'PIN, 0.5 mrad')
plot(a_m, Ptx_variable_APD[2,:],'-o', label = 'APD, 2 mrad')
plot(a_m, Ptx_variable_PIN[2,:],'-*', label = 'PIN, 2 mrad')
xlabel('Rx diameter (cm)'); ylabel('P_tx (dBm)')
legend()
grid()
plt.show()
Сравнение со случаем электро-магнитного межспутникового канала можно посмотреть в нашей статье в журнале. Там же описаны причины, почему в итоге от такого сценария мы отказались, но об этом я скажу и здесь. Скрипты и формулы есть также в моем репозитории в формате jupyter-notebook — вдруг кому пригодится.
Подводные камни
И вот мы, потрепанные справочниками и математическими формулами, но всё же окрыленные полученными результатами (да что там — самим фактом красивых графиков!), назначаем финальную встречу перед защитой. И сталкиваемся с новым витком важных деталей…
Н.п. №2: Ну, хорошо, это понятно, что есть выигрыши. Убедили, что есть уже и какая-то аппаратная база. А что с нацеливанием? Вы, наверное, слышали про PAT-систему (Pointing, Acquisition, and Tracking).
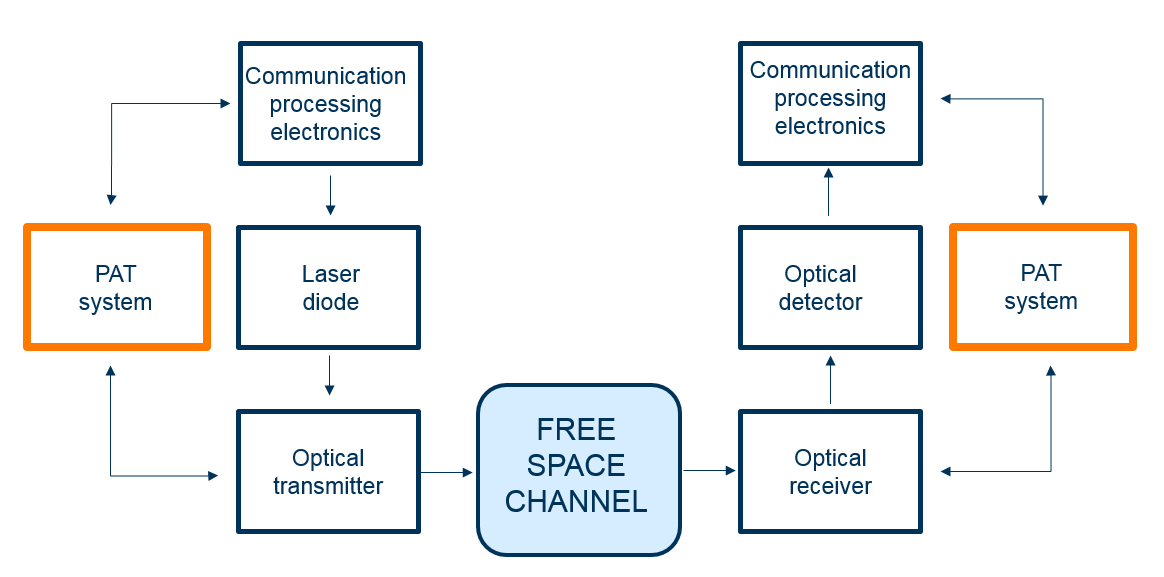
Рис. 6. Упрощенная схема системы беспроводной оптической приёмопередачи.
Н.п. №2: Да, есть примеры оптических каналов для больших спутников [4], однако, в этом случае вы можете позволить себе и больший диаметр приёмника, и больший угол расходимости лазера, и большую мощность передачи. Более того, сам CubeSat, я думаю, очень сильно вибрирует при движении. Для радиоканала на относительно небольших частотах это, может, и не существенно, однако, для оптики — сами понимаете. Существует ли такая точная стабилизация и PAT-система на данный момент?
И мы сильно призадумались...
Н.п. №2: Вот что, по своей части я вам положительную оценку ставлю. Однако, мой вам совет: спускайтесь с небес на землю...
И мы, измотанно выдохнув, спустились: проект со спутниковой оптикой решили не продолжать. Тем более, что, видимо, у всех за время частых встреч накопилось некоторое выгорание...
Однако, нет-нет да и проскользнет, так сказать, в сердце нотка студенческой надежды, что "препод" был-таки неправ в своем скепсисе. Нет-нет да и хочется найти в достижениях современной техники ту самую концепцию. "И взор устремляется ввысь"...

Литература
Janson S. W., Welle R. P. The NASA optical communication and sensor demonstration program: an update //28th Annual AIAA/USU Conference on Small Satellites. – 2014. – С. 4-7.
Wolf, M., & Kreß, D. (2003). Short-range wireless infrared transmission: the link buoget compared to RF. IEEE wireless communications, 10(2), 8-14.
https://www.nii.ac.jp/qis/first-quantum/forStudents/lecture/pdf/noise/chapter12.pdf
Smutny B. et al. 5.6 Gbps optical intersatellite communication link //Free-Space Laser Communication Technologies XXI. – International Society for Optics and Photonics, 2009. – Т. 7199. – С. 719906.









