США, Техас, Остин, клуб Continental
Воскресенье, 5 января 1987 г.
— Спасибо за приглашение, мистер Ломуто. Скоро я возвращаюсь в Англию, так что это было очень вовремя.
— Спасибо, что согласились со мной встретиться, мистер… сэр… Чарльз… Энтони Ричард… Хоар. Это большая честь для меня. Я даже не знаю, как к вам обращаться. У вас есть рыцарский титул?
— Зовите меня Тони, и, если вы позволите, я буду называть вас Нико.
На первый взгляд — обычная картина: два человека наслаждаются виски. Однако внимательному наблюдателю открываются интригующие подробности. Прежде всего — напряжение, которое можно было резать ножом.
Одетый в безупречно подогнанный костюм-тройку с нарочитой небрежностью, на какую способен только англичанин, Тони Хоар был таким же воплощением Британии, как и чашка чая. Смиренное выражение лица, с которым он попивал из своего стакана, без всяких слов выражало его мнение в споре между бурбоном и скотчем. Сидевший напротив Нико Ломуто представлял полную ему противоположность: одетый в джинсы программист, мешавший виски с колой (что для Тони было настолько возмутительно, что он сразу решил подчёркнуто это игнорировать — как резкий запах пота или оскорбительную татуировку), в состоянии некого расслабленного трепета перед гигантом информатики, с которым он только что познакомился лично.
— Послушайте, Тони, — сказал Нико после того, как иссякли темы для обычной лёгкой беседы. — По поводу того алгоритма разбиения. Я даже не собирался его публиковать...
— Что? Ах да, алгоритм разбиения, — Тони поднял брови в притворном изумлении, словно забыв, что каждая статья или книга о быстрой сортировке за последние пять лет упоминала их имена вместе. Очевидно, что именно это связывало этих двух людей и было причиной этой встречи, но Тони, как безупречный джентльмен, мог бы часами говорить о погоде, если бы собеседник не упомянул о стоящем в комнате розовом слоне.
— Да, тот самый алгоритм разбиения, который постоянно вспоминают в связи с вашим, — продолжал Нико. — Я не большой теоретик в области алгоритмов. Я работаю над Ada, и всю эту штуку с разбиением придумал только для развлечения. Но что меня беспокоит, — говорил Нико непринуждённым тоном человека, которому нечего скрывать, — что этот алгоритм ничем не лучше. Моя схема разбиения всегда делает столько же сравнений и по крайней мере столько же обменов, сколько и ваша. В худшем случае мой алгоритм делает n дополнительных обменов — n! Я не понимаю, почему его продолжают вспоминать. Я уже ничего не могу с этим сделать. Я не знаю, каким алгоритмам стоит учить студентов. Это как сортировка пузырьком. Каждый раз, когда кто-то упоминает быструю сортировку, в аудитории обязательно оказывается какой-то пустоголовый (или пузырькоголовый?) болван, который скажет: а я ещё слышал про сортировку пузырьком. У меня от этого кровь вскипает.
Нико вздохнул. Тони кивнул. Собеседники нашли общий язык. Взаимопонимание заполнило воздух так же внезапно, тихо и приятно, как запах печенья из духовки. Часы тикали. С одной стороны стола Нико потягивал свой виски с колой. С другой — Тони попивал бурбон со всё тем же выражением лица.
Тони заговорил, тщательно выбирая слова, как учёный, стремящийся рассмотреть каждую гипотезу:
— Я понимаю, Нико. Но подумайте вот о чём. Ваш алгоритм прост и постоянен, двигается в одном направлении и делает по крайней мере один обмен каждый шаг. Возможно, в будущем появятся машины, которые...
— Неважно, какая машина: меньшее количество обменов всегда лучше, чем большее. Это просто здравый смысл, — категорически возразил Нико.
— Я бы не был так уверен. Компьютеры не руководствуются здравым смыслом. Порой они удивляют. Надо полагать, что и дальше будут удивлять. А сейчас давайте наслаждаться этим вечером. Нет ничего лучше интересной беседы в тихом клубе.
— Согласен. Хорошее место. Скоро должна начаться живая музыка в стиле кантри.
— Прелестно, — к собственному изумлению Тони выдавил вежливую улыбку.
США, Массачусетс, Честнат-Хилл
Наши дни
Многие годы я живу с тщательно скрываемой зависимостью от проблем сортировки. Скрыть её было нетрудно: нездоровый интерес к вопросам сортировки — социально приемлемая форма профессиональной деформации. Уверен, что немало программистов потратили одну или две бессонных ночи, чтобы попробовать ещё одну идею сортировки, которая уж точно окажется лучше всех остальных. Потому никто не повёл бровью, когда ещё в 2002 году я написал о сортировке. (Слышали про fit pivot? Конечно же не слышали). Никто не стал вмешиваться, когда я разработал функцию std.sort в D, которая, как оказалось, в некоторых случаях выдавала квадратичную сложность (с тех пор это, к счастью, исправлено). Никто не поднял шума даже когда я написал научную статью о задаче выбора (которая рука об руку идёт с задачей сортировки), будучи независимым участником конференции, чем впечатлил даже организаторов. И даже мой доклад о сортировке на CppCon 2019 не вызвал публичного скандала. Программисты — свои люди, они всё понимают.
Я стараюсь соблюдать воздержание. Как там говорят, «жить по одному дню»? Но всё же я почувствовал внутри себя волнение, когда увидел заголовок одной недавней статьи: «Ошибки в предсказании переходов не затрагивают сортировку слиянием» (Branch Mispredictions Don’t Affect Mergesort). Какое заманчивое название. Для начала: а что, ошибки в предсказании переходов должны были затрагивать сортировку слиянием? Я понятия не имел, главным образом потому что все вплоть до вашей бабушки используют быструю сортировку, так что сортировка слиянием никогда не попадала в поле моего внимания. Но слушайте, мне об этом даже не нужно волноваться, потому что заголовок говорит, что проблема, о существовании о которой я даже не знал, вовсе не является проблемой. Так что в этом смысле заголовок сам себя отменяет. Но я всё же прочитал статью (и вам тоже советую), и помимо многих других интересных вещей кое-что особенно зацепило моё внимание: схема разбиения Ломуто рассматривалась как серьёзный соперник повсеместно используемому разбиению Хоара с точки зрения эффективности. Эффективности!
Оказывается, современные компьютерные архитектуры иногда действительно идут наперекор здравому смыслу.
Разбить, быть может, отсортировать
Давайте по-быстрому пробежимся по двум схемам разбиения. Разбить массив значит организовать элементы так, чтобы все элементы, меньшие или равные опорному элементу, были слева от него, а элементы, большие или равные ему, — справа. Окончательная позиция опорного элемента должна быть на границе разбиений. (Если есть несколько равных опорных элементов, то окончательная позиция может разниться, из чего вытекают практические последствия, но в данной дискуссии можно принять, что все значения в массиве уникальны).
Схема разбиения Ломуто проходится по массиву слева направо, сохраняя индексы «чтения» и «записи», начинающиеся с 0. Каждый считываемый элемент сравнивается с опорным: если он больше, то он пропускается (индекс чтения переходит на шаг вперёд). В противном случае значение под индексом чтения меняется местами со значением под индексом записи, и оба индекса передвигаются на шаг вперёд. Когда чтение закончено, индекс записи определяет место разбиения. В качестве иллюстрации — анимация ниже (сделано пользователем Википедии под ником Mastremo, используется без изменений согласно лицензии CC-BY-SA 3.0).

Проблема с разбиением Ломуто в том, что оно может делать ненужные обмены. Возьмём экстремальный случай, когда только самый первый слева элемент больше опорного. Каждая итерация алгоритма будет неуклюже перемещать этот элемент на одну позицию вправо, подобно, эм, сортировке пузырьком.
Схема разбиения Хоара элегантно решает эту проблему, итерируя массив с двух сторон двумя парами индексов «чтения» и «записи». Алгоритм пропускает элементы, которые уже находятся в положенных местах (слева — меньше, справа — больше) и меняет местами только меньший элемент слева с б́ольшим элементом справа. Когда индексы встречаются, массив разбит вокруг места встречи. Большинство современных реализаций быстрой сортировки используют разбиение Хоара, по очевидным причинам: оно делает столько же сравнений, что и разбиение Ломуто, и меньше обменов.
Учитывая, что разбиение Хоара очевидно делает меньше работы, чем разбиение Ломуто, возникает вопрос, зачем тогда вообще учить студентов последнему. Александр Степанов — создатель STL — написал отличную статью о разбиении и привёл аргумент об обобщённости: для разбиения Ломуто достаточно итерирования в одну сторону, тогда как разбиение Хоара требует двунаправленного итерирования. Это ценная мысль, хотя её практическая ценность невелика: да, вы можете использовать разбиение Ломуто на односвязных списках, но обычно разбиение делают ради быстрой сортировки, а для односвязных списков быстрая сортировка — плохой выбор, здесь лучше подойдёт сортировка слиянием.
И всё же существует очень практичный — и очень неожиданный — довод в пользу разбиения Ломуто, и в нём заключается гвоздь всей статьи: если реализовать разбиение Ломуто без ветвления, то на случайных данных оно становится намного быстрее разбиения Хоара. Учитывая, что быстрая сортировка большую часть времени тратит на разбиение, то это сулит нам солидный выигрыш в производительности быстрой сортировки (да, я говорю об индустриальных реализациях в стандартных библиотеках в C++ и D), если мы заменим алгоритм разбиения на тот, который буквально делает больше работы.
Вы всё правильно прочитали.
Время расчехлить код
Давайте посмотрим на аккуратную реализацию разбиения Хоара. Чтобы исключить все лишние подробности, код в этой статье написан для типа long в качестве элемента и использует простые указатели. Он компилируется и работает одинаково что в C++, что в D. Код в этой статье останется универсальным для обоих языков, поскольку исследовательская литература часто использует в качестве стандарта std::sort из C++.
/** Partition using the minimum of the first and last element as pivot. Returns: a pointer to the final position of the pivot. */ long* hoare_partition(long* first, long* last) { assert(first <= last); if (last - first < 2) return first; // nothing interesting to do --last; if (*first > *last) swap(*first, *last); auto pivot_pos = first; auto pivot = *pivot_pos; for (;;) { ++first; auto f = *first; while (f < pivot) f = *++first; auto l = *last; while (pivot < l) l = *--last; if (first >= last) break; *first = l; *last = f; --last; } --first; swap(*first, *pivot_pos); return first; }
Возможно, выбор опорного элемента покажется вам странным, но не волнуйтесь: обычно используется более сложная схема (например, медиана трёх значений), но для основного цикла важно лишь, чтобы опорный элемент не был самым большим элементом массива. Это позволит основному циклу опустить некоторые проверки без риска выйти за пределы массива.
Эффективность этой реализации заслуживает многих похвал (и вероятно, именно такой код, с минимальными отличиями, вы увидите в стандартных библиотеках C++ и D). По этому коду видно, что его написали люди, которые ничего в своей жизни не делают просто так. Люди, которые аккуратно стригут ногти, приходят когда обещают прийти и регулярно звонят маме. Которые делают упражнения ушу каждое утро и не дают ни одному циклу компьютера уйти впустую. В этом коде нет ни одной торчащей нитки. Генерируемый ассемблер исключительно ёмок и почти одинаков для C++ и D. Отличия есть только между бэкендами: LLVM (clang и ldc) показывает небольшое преимущество по размеру перед gcc (g++ и gdc).
Ниже показана черновая версия разбиения Ломуто, которая хорошо подходит для объяснения, но не очень эффективна:
/** Choose the pivot as the first element, then partition. Returns: a pointer to the final position of the pivot. */ long* lomuto_partition_naive(long* first, long* last) { assert(first <= last); if (last - first < 2) return first; // nothing interesting to do auto pivot_pos = first; auto pivot = *first; ++first; for (auto read = first; read < last; ++read) { if (*read < pivot) { swap(*read, *first); ++first; } } --first; swap(*first, *pivot_pos); return first; }
Начать с того, что этот код будет делать слишком много бессмысленных обменов (обменов элемента массива с самим собой), если несколько элементов слева окажутся больше опорного элемента. Всё это время first будет равно write, и менять местами *first с *write будет пустой тратой времени. Давайте исправим это, добавив предварительный цикл, который будет пропускать неинтересное начало массива:
/** Partition using the minimum of the first and last element as pivot. Returns: a pointer to the final position of the pivot. */ long* lomuto_partition(long* first, long* last) { assert(first <= last); if (last - first < 2) return first; // nothing interesting to do --last; if (*first > *last) swap(*first, *last); auto pivot_pos = first; auto pivot = *first; // Prelude: position first (the write head) on the first element // larger than the pivot. do { ++first; } while (*first < pivot); assert(first <= last); // Main course. for (auto read = first + 1; read < last; ++read) { auto x = *read; if (x < pivot) { *read = *first; *first = x; ++first; } } // Put the pivot where it belongs. assert(*first >= pivot); --first; *pivot_pos = *first; *first = pivot; return first; }
Теперь функция выбирает в качестве опорного меньший из первого и последнего элементов, прямо как hoare_partition. Я также сделал ещё одно небольшое изменение: вместо функции swap будем использовать явное присваивание. Оптимизатор позаботится обо всём автоматически, зато мы более чётко увидим сравнительно дорогие операции над элементами массива. Теперь к интересной части. Сфокусируемся на основном цикле:
for (auto read = first + 1; read < last; ++read) { auto x = *read; if (x < pivot) { *read = *first; *first = x; ++first; } }
Подумаем о статистике. В этом цикле две проверки условия: read < last и x < pivot. Насколько они предсказуемы? Что ж, первая из них чрезвычайно предсказуема: можно с надёжностью предсказать, что результат всегда будет истинным, и мы ошибёмся только один раз вне зависимости от размера массива. Разработчики компиляторов и проектировщики железа об этом знают и планируют самый быстрый путь, исходя из предположения, что цикл будет продолжаться. (Идея подарка для вашего друга — инженера из Intel: дверной коврик с надписью «Переход назад всегда будет выполнен»). Процессор начнёт выполнять следующую итерацию цикла ещё до того, как определит, должен ли цикл продолжаться. Лишняя работа будет выброшена только один раз в конце цикла. В этом заключается магия спекулятивного выполнения.
Со второй проверкой — x < pivot — всё не так радужно. Со случайными данными и случайно выбранным опорным элементом результат может быть любым с равной вероятностью. Это значит, что спекулятивное выполнение здесь не поможет, что очень плохо для производительности. Насколько плохо? В архитектурах с многоступенчатыми конвейерами (а на сегодняшний день они все такие) ошибка предсказания означает, что работу, проделанную несколькими стадиями конвейера, придётся выбросить, и этим мы запустим пузырёк бесполезности через весь конвейер (представьте пузырьки воздуха в садовом шланге). Если этих пузырьков станет слишком много, цикл будет выдавать только часть от достижимой производительности. Как покажут измерения, одно лишнее предсказание забирает около 30% потенциальной скорости.
Как нам исправить эту проблему? Вот идея: вместо того, чтобы принимать решения, контролирующие ход выполнения, мы напишем код прямолинейно и оформим решения как целые числа, которые будут направлять данные при помощи аккуратной индексации. Готовьтесь: нам придётся делать глупые вещи. Например, каждую итерацию вместо того, чтобы в зависимости от условия делать либо две записи, либо ноль, мы будем делать ровно две записи независимо ни от чего. Если записи не требуются, мы будем перезаписывать данные в памяти их собственными значениями (я говорил про «глупые вещи»?). Чтобы подготовить к этому код, перепишем его следующим образом:
for (auto read = first + 1; read < last; ++read) { auto x = *read; if (x < pivot) { *read = *first; *first = x; first += 1; } else { *read = x; *first = *first; first += 0; } }
Теперь обе ветви в цикле практически одинаковы, не считая данных. Код всё ещё корректен (хоть он и странный), потому что ветвь else впустую переписывает *read и *first самими собой. Как нам объединить две ветви? Чтобы сделать это эффективно, придётся немного подумать и поэкспериментировать. Увеличить first на единицу в зависимости от условия несложно: first += x < pivot. Проще простого. Справиться с двумя записями в память уже труднее, но основная идея в том, чтобы взять разницу между указателями и использовать индексацию. Вот получившийся код. Потратьте минуту, чтобы его осмыслить:
for (; read < last; ++read) { auto x = *read; auto smaller = -int(x < pivot); auto delta = smaller & (read - first); first[delta] = *first; read[-delta] = x; first -= smaller; }
Перефразируя крылатое латинское выражение, explanatio longa, codex brevis est. Краток код, объяснение длинно. Инициализация smaller через -int(x < pivot) выглядит странно, но для неё есть хорошая причина: smaller можно использовать и как целое (0 или −1) для обычной арифметики, и как маску со значением 0x0 или 0xFFFFFFFF (то есть все биты выставлены либо на 0, либо на 1) для побитовых операций. Мы будем использовать эту маску, чтобы пропустить или не пропустить другое целое при вычислении delta. Если x < pivot, то smaller — это все единицы, и delta инициализируется как read - first. Далее delta используется в first[delta] и read[-delta] — на самом это деле просто синтаксический сахар для *(first + delta) и *(read - delta). Если заменить delta в этих выражениях, получим соответственно *(first + (read - first)) и *(read - (read - first)).
Последняя строчка — first -= smaller — тривиальна: если x < pivot, то отнять от first −1, что то же самое, что и увеличить first на 1. В противном случае отнять от first 0, что не окажет никакого эффекта.
Если заменить x < pivot на 1, то вот что происходит в теле цикла:
auto x = *read; int smaller = -1; auto delta = -1 & (read - first); *(first + (read - first)) = *first; *(read - (read - first)) = x; first -= -1;
Почти по волшебству две операции над указателями упрощаются до *read и *first, так что два присваивания складываются в обмен (не забывайте, что x только что инициализировали значением *read). Это именно то, что мы делали в ветви «if» в первоначальной версии!
Если x < pivot — ложь, то delta инициализируется нулём, и тело цикла работает так:
auto x = *read; int smaller = 0; auto delta = 0 & (read - first); *(first + 0) = *first; *(read - 0) = x; first -= 0;
На этот раз всё проще: *first и *read переписывается самими собой, а с first ничего не происходит. Весь этот код ничего не делает, и это как раз то, что нам было нужно.
Теперь посмотрим на всю функцию:
long* lomuto_partition_branchfree(long* first, long* last) { assert(first <= last); if (last - first < 2) return first; // nothing interesting to do --last; if (*first > *last) swap(*first, *last); auto pivot_pos = first; auto pivot = *first; do { ++first; assert(first <= last); } while (*first < pivot); for (auto read = first + 1; read < last; ++read) { auto x = *read; auto smaller = -int(x < pivot); auto delta = smaller & (read - first); first[delta] = *first; read[-delta] = x; first -= smaller; } assert(*first >= pivot); --first; *pivot_pos = *first; *first = pivot; return first; }
Красиво, правда? Ещё более красив сгенерированный код: взгляните на clang/ldc и g++/gdc. Опять же, между бэкендами наблюдается небольшая разница.
Эксперименты и результаты
Весь код доступен здесь: https://github.com/andralex/lomuto.
Чтобы устроить честное сравнение двух схем разбиения, я написал реализацию быстрой сортировки, поскольку именно для неё чаще всего используется разбиение. Для простоты я опустил некоторые детали, присутствующие в индустриальных имплементациях быстрой сортировки, нужные для данных с разными характеристиками (частично отсортированные в прямом или обратном порядке, с локальными паттернами, со множеством дубликатов). Библиотечные реализации тщательно выбирают опорный элемент, обычно из 3—9 элементов, иногда с рандомизацией. Они умеют определять проблемные вводные данные и избегать их, обычно с помощью интроспективной сортировки.
Наш бенчмарк для простоты проводит тест только на случайных данных, и опорный элемент выбирается просто как меньшее значение из первого и последнего элементов. Репрезентативность при этом не страдает: более качественный выбор опорного элемента и добавление интроспекции делаются одинаково вне зависимости от метода разбиения. Наш главный интерес — сравнить производительность Хоара, Ломуто и версии Ломуто без ветвления.
Графики ниже показывают время, затраченное на одну сортировку в зависимости от объёма входных данных. Используемая машина: Intel i7-4790 на частоте 3600 МГц с иерархией кэша 256 Кб / 1 Мб / 8 Мб, работающий под Ubuntu 20.04. Все билды были настроены на максимальную скорость (-O3, без проверок assert и проверок границ массивов в D). Входные данные — псевдослучайная последовательность значений типа long с одинаковым зерном для всех языков и платформ. Для устранения шума были взяты минимальные значения за несколько эпох.
Ниже показаны результаты для языка D, включая std.sort из стандартной библиотеки в качестве базовой величины.
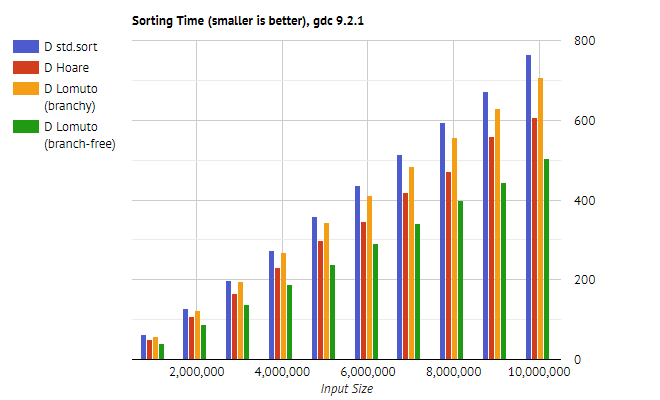
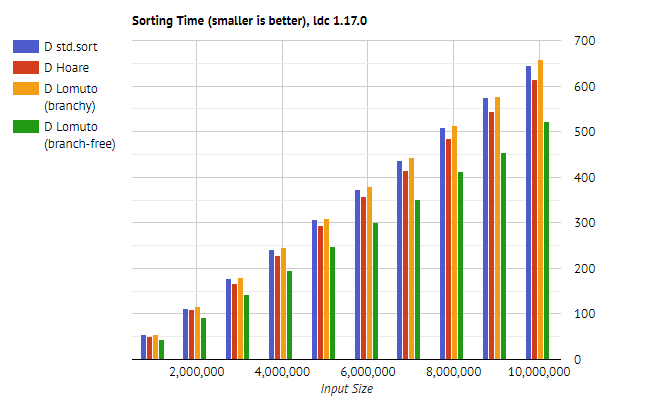
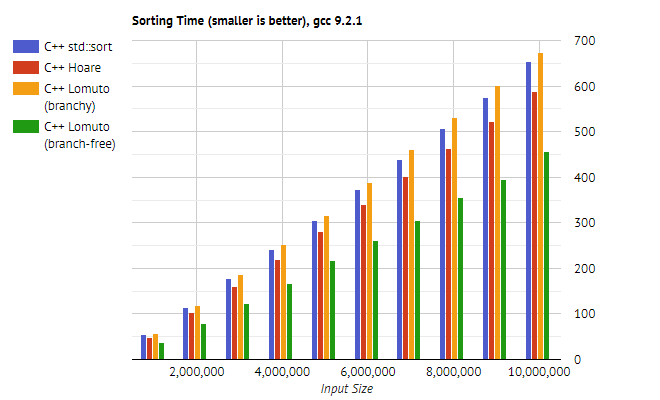
Ниже показаны результаты для C++. Опять же, для сравнения взята функция std::sort из стандартной библиотеки.

Важная метрика — эффективность использования CPU, которую Intel VTune показывает в виде диаграммы-воронки. VTune выдаёт очень подробные отчёты, но диаграмма-воронка наглядно показывает, на что уходит работа. Чем ́уже выход (справа), тем медленнее выполняется программа по сравнению с её возможным потенциалом.
Диаграммы ниже соответствуют разбиению Хоара, разбиению Ломуто (в традиционной реализации) и разбиению Ломуто без ветвления. Первые два выбрасывают примерно 30% всей работы из-за ошибок предсказания. По сравнению с ними версия разбиения Ломуто без ветвления почти ничего не выбрасывает, что позволяет ей быть эффективнее несмотря на большее количество записей в память.

Диаграмма-воронка для разбиения Хоара. Значительная часть работы проделана впустую из-за ошибок предсказания переходов.
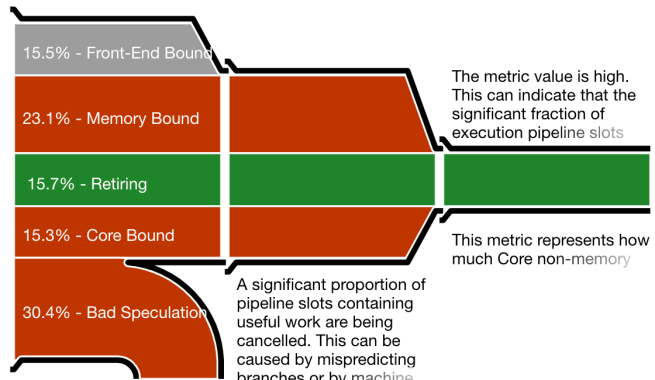
Диаграмма-воронка для традиционной реализации разбиения Ломуто. Примерно столько же ошибок предсказания переходов, что и в разбиении Хоара.
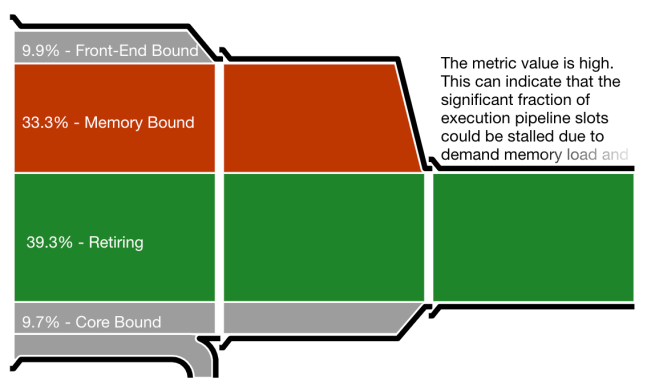
Диаграмма-воронка для реализации разбиения Ломуто без ветвления. Практически ничего не уходит впустую из-за ошибок предсказания переходов, что даёт гораздо б́ольшую эффективность.
Обсуждение
Четыре версии (два языка помноженные на два бэкенда) показывают слабые отличия из-за различиях в реализации стандартных библиотек и в бэкендах. Не вызывает удивления, что незначительные различия в генерируемом коде могут создавать измеряемую разницу в скорости выполнения.
Как и ожидалось, обычная версия разбиения Ломуто показывает себя хуже, чем разбиение Хоара, особенно на большом объёме входных данных. И то, и то, находятся в одной лиге, когда идёт речь о реализации функции сортировки в стандартной библиотеке. Однако версия разбиения Ломуто без ветвления побеждает с большим отрывом вне зависимости от платформы, бэкенда и объёма входных данных.
За последние годы стало совершенно очевидно, что анализ алгоритмов (из которого вытекают предложения по оптимизации) нельзя проводить на бумаге, используя упрощённые модели компьютерных архитектур. На эффективность сортировки влияет не только количество сравнений и обменов — как минимум представляет важным учитывать предсказуемость сравнений. Я надеюсь, что в будущем появятся более реалистичные модели, которые позволят теоретикам править балом. А на сегодняшний день, к сожалению, над оптимизацией алгоритмов всё ещё приходится работать экспериментальным путём.
Что касается сортировки, то Ломуто определённо возвращается, и его стоит принимать в расчёт тем, кто разрабатывает индустриальные реализации быстрой сортировки на архитектурах со спекулятивным выполнением.
Благодарности
Большое спасибо Amr Elmasry, Jyrki Katajainen и Max Stenmark за их вдохновляющую статью. Мне пока не удалось написать реализацию сортировки слиянием (основной результат их статьи), который мог бы поспорить с описанной здесь быстрой сортировкой, но я над этим работаю. (Да простит меня Общество анонимных сортировщиков… Я опять сорвался). Также хочу поблагодарить Майкла Паркера и всех авторов комментариев к оригинальной публикации за то, что исправили многие мои языковые косяки — английский для меня не родной. (Как обычно говорят: «pretend not to notice» или «pretend to not notice»? Каждый раз забываю). И конечно, основная заслуга принадлежит Нико Ломуто, который придумал алгоритм, который не просто прошёл проверку временем — он его опередил.
