EmMur 18 июн 2022 в 02:19

Простейшая модель броуновского движения и фракталы

4 мин

4.9K

Этот пост является выжимкой из моей курсовой работы по исследованию броуновского движения. Хотя задание было сформулировано как простое написание программы для одномерного и двумерного случаев броуновского движения, мне показалось интересным рассмотреть простейшую дискретную аппроксимацию броуновского движения - одномерное случайное блуждание - через фрактальную геометрию и определить его фрактальную размерность.

Историческая справка

Само понятие броуновского движения датируется 1827 годом, когда шотландский ботаник Роберт Броун исследовал движение пыльцевых зерен в жидкости. Исследуя пыльцу под микроскопом, он установил, что в растительном соке плавающие пыльцевые зерна двигаются совершенно хаотически, зигзагообразно. Он посчитал, что эти частички живые. Истинную же причину броуновского движения объяснили Альберт Эйнштейн (в 1905 году) и Мариан Смолуховский (в 1906). Ученые использовали существенно отличающиеся методологические подходы, которые, тем не менее, часто приводили к полностью или частично совпадающим результатам, а иногда дополняли друг друга. В своей работе Эйнштейн получил формулу для зависимости смещения броуновской частицы от времени:

$\langle r^2\rangle=6\kappa TBt,$

где- постоянная Больцмана,- температура, - время, а- подвижность частицы.

После получения формулы Эйнштейна в научном сообществе XX века встал вопрос о строгой математической теории броуновского движения. Так в 1923 году Норберт Винер построил первую удовлетворительную с математической точки зрения модель выборочных реализаций и доказал их почти наверное непрерывность.

Почти наверное здесь - это математический термин обозначающий, что если какое-либо свойство выполняется для каждой точки данного множества, исключая, быть может, множество меры нуль, то говорят, что это свойство выполняется на данном множестве почти наверное или почти всюду.

Простейшая реализация броуновского движения

Простейшей дискретной аппроксимацией броуновского движения служит одномерное случайное блуждание. Мы располагаем частицу в точке. Далее частица совершает шаг влево или вправо в зависимости от случайного выбора. Случайное блуждание происходит итеративно. Для каждого шагаположим

$x_{n}=x_{n-1}\pm 1.$

Далее будем называть такую реализацию броуновского движения простейшей.

Броуновское движение и распределение Гаусса

Броуновское движение по сути своей имеет гауссовскую природу. Но всегда ли возможно такое обобщение?
Для начала дадим определение одномерному броуновскому движению как гауссовскому процессу.
Итак, гауссовский процессназывается одномерным броуновским движением, или винеровским процессом на интервале, если он обладает следующими свойствами:

и функцияпочти всегда непрерывна.
Свойство гауссовости приращений: случайная величина

$\Delta X=X(t_{2})-X(t_{1}),\ t_{2}>t_{1},$

имеет гауссовское распределение с математическим ожидание 0 и дисперсией $\sigma^2(t_{2}-t_{1})$ , где $\sigma$ - положительная константа.

То есть

$P(\Delta X < x)=\frac{1}{\sqrt{2\pi\sigma^2 (t_{2}-t_{1})}}\int_{x}^{-\infty}exp\Big(-\frac{u^2}{2\sigma^2 (t_{2}-t_{1})}\Big)du$

Впоследствии будем называть данное броуновское движение классическим.

Как видим, ответ на наш вопрос уже содержится в определении. Да, действительно такое обобщение не находит примера-контраргумента по определению. Тогда перефразируем и уточним свой вопрос: Любая ли модель броуновского движения является гауссовой?

Фрактальное броуновское движение

Для ответа на вопрос из предыдущего раздела дадим определение более широкому классу гауссовских процессов таких как фрактальное броуновское движение.

Так гауссовский процесс называется одномерным фрактальным броуновским движением, или винеровским процессом на интервале, если он обладает следующими свойствами:

и функция почти всегда непрерывна.
Свойство гауссовости приращений: случайная величина

$\Delta X=X(t_{2})-X(t_{1}),\ t_{2}>t_{1}$

имеет гауссовское распределение с математическим ожиданиеи дисперсией $\sigma^2(t_{2}-t_{1})^{2H}$ , где $\sigma$ - положительная константа.

То есть

$P(\Delta X < x)=\frac{1}{\sqrt{2\pi}\sigma (t_{2}-t_{1})^{H}}\int_{x}^{-\infty}exp\Big(-\frac{u^2}{2\sigma^2 (t_{2}-t_{1})^{H}}\Big)du$ $P(\Delta X < x)=\frac{1}{\sqrt{2\pi}\sigma (t_{2}-t_{1})^{H}}\int_{x}^{-\infty}exp\Big(-\frac{u^2}{2\sigma^2 (t_{2}-t_{1})^{H}}\Big)du$

Как видно из определения фрактальное броуновское движение с параметромсовпадает с классическим броуновским движением. Также как и в предыдущем разделе ответ на наш вопрос лежит в самом определении и он вновь положителен. Но самый интересный вопрос на который получилось найти ответ звучит так: является ли простейшее броуновское движение классическим? Для ответа на этот вопрос был реализован алгоритм.

Получение фрактальной размерности

График зависимости координаты частицы от времени в одномерном случае

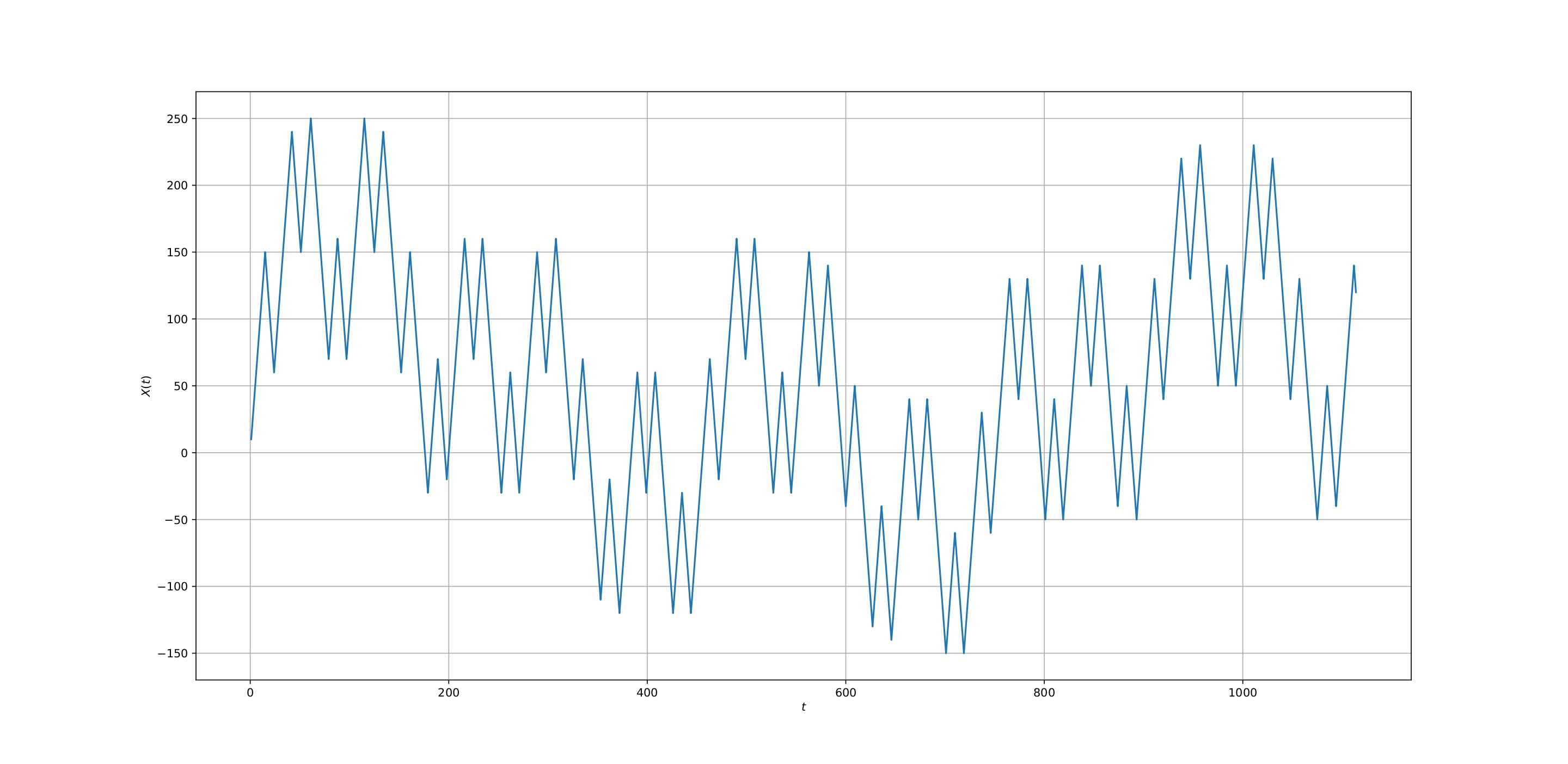
Назначение алгоритмавычислять параметрдля одномерного фрактального броуновсrого движения (далее ФБД). На вход ему будет подается вектор, представляющий ФБД и его длина, на выходе получим. Все данные мы получим из графика. Чтобы определить фрактальную размерность для одномерного случая нужно из двойки вычесть. То есть. В нашем случае $H \approx 0.84$ приитераций и лучим $D\approx1.16$ . Это говорит о том что простейшая модель броуновского движения является гауссовским процессом, так как условиевыполняется. Но простейшая модель броуновского движения не является классическим броуновским движением.

Еще на что стоит обратить внимание так это то, что фрактальная размерность не всегда постоянная величина. Существуют так называемые масштабно-неразмерные фракталы, фрактальная величина которых зависит от масштаба. В нашем случае масштаб определяется количеством итераций. В проведенных мною экспериментах при итераций фрактальная размерность, как уже было сказано выше была около величины (, при $H\approx0.84$ ). Но с ростом числа итераций, примерно при, она стала примерно. Это приводит нас к выводу о том, что простейшая модель броуновского движения есть масштабно-неразмерный фрактал.