Декартово дерево: Часть 1. Описание, операции, применения

Оглавление (на данный момент)

Часть 1. Описание, операции, применения.
Часть 2. Ценная информация в дереве и множественные операции с ней.
Часть 3. Декартово дерево по неявному ключу.
To be continued...

Декартово дерево (cartesian tree, treap) — красивая и легко реализующаяся структура данных, которая с минимальными усилиями позволит вам производить многие скоростные операции над массивами ваших данных. Что характерно, на Хабрахабре единственное его упоминание я нашел в обзорном посте многоуважаемого winger, но тогда продолжение тому циклу так и не последовало. Обидно, кстати.

Я постараюсь покрыть все, что мне известно по теме — несмотря на то, что известно мне сравнительно не так уж много, материала вполне хватит поста на два, а то и на три. Все алгоритмы иллюстрируются исходниками на C# (а так как я любитель функционального программирования, то где-нибудь в послесловии речь зайдет и о F# — но это читать не обязательно :). Итак, приступим.

Введение

В качестве введения рекомендую прочесть пост про двоичные деревья поиска того же winger, поскольку без понимания того, что такое дерево, дерево поиска, а так же без знания оценок сложности алгоритма многое из материала данной статьи останется для вас китайской грамотой. Обидно, правда?

Следующий пункт нашей обязательной программы — куча (heap). Думаю, также многим известная структура данных, однако краткий обзор я все же приведу.
Представьте себе двоичное дерево с какими-то данными (ключами) в вершинах. И для каждой вершины мы в обязательном порядке требуем следующее: ее ключ строго больше, чем ключи ее непосредственных сыновей. Вот небольшой пример корректной кучи:

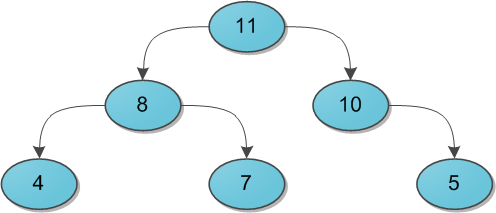
На заметку сразу скажу, что совершенно не обязательно думать про кучу исключительно как структуру, у которой родитель больше, чем его потомки. Никто не запрещает взять противоположный вариант и считать, что родитель меньше потомков — главное, выберите что-то одно для всего дерева. Для нужд этой статьи гораздо удобнее будет использовать вариант со знаком «больше».

Сейчас за кадром остается вопрос, каким образом в кучу можно добавлять и удалять из нее элементы. Во-первых, эти алгоритмы требуют отдельного места на осмотр, а во-вторых, нам они все равно не понадобятся.

Проблемы

Когда речь заходит о деревьях поиска (вы же уже прочитали рекомендуемую статью, правда?), основной вопрос, который ставится перед структурой — скорость выполнения операций, вне зависимости от данных, хранящихся в ней, и последовательности их поступления. Так, двоичное дерево поиска дает гарантию, что поиск конкретного ключа в этом дереве будет выполняться за O(H), где H — высота дерева. Но какой может быть эта высота — черт его знает. При неблагоприятных обстоятельствах высота дерева легко может стать N (количество элементов в нем), и тогда дерево поиска вырождается в обычный список — и зачем оно тогда нужно? Для достижения такой ситуации достаточно добавлять в дерево поиска элементы от 1 до N в очереди возрастания — при стандартном алгоритме добавления в дерево получим следующую картинку:

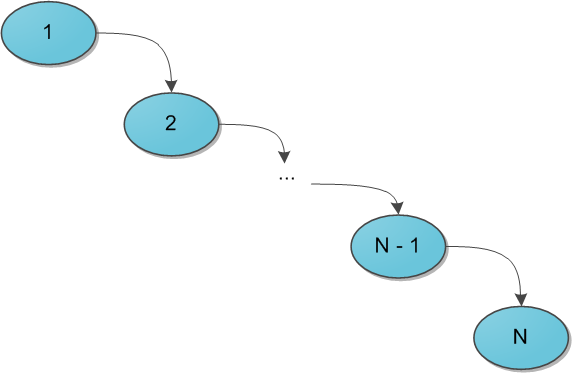
Было придумано огромное количество так называемых сбалансированных деревьев поиска — грубо говоря, тех, в которых по мере существования дерева при каждой операции над ним поддерживается оптимальность максимальной глубины дерева. Оптимальная глубина имеет порядок O(log₂ N) — тогда тот же порядок имеет время выполнения каждого поиска в дереве. Структур данных, поддерживающих такую глубину, много, самые известные тут красно-черное дерево или AВЛ-дерево. Их отличительная черта в большинстве — трудная реализация, основанная на размере чертовой кучи случаев, в которых можно и запутаться. Своей же простотой и красотой выгодно отличается, наоборот, декартово дерево, и даже дает нам в некотором роде то самое желанное логарифмическое время, но лишь с достаточно высокой вероятностью… впрочем, о таких деталях и тонкостях позже.

Определение

Итак у нас есть данные дерева — ключи x (здесь и далее предполагается, что ключ и является той самой информацией, которую мы храним в дереве; когда впоследствии потребуется отделять по смыслу пользовательскую информацию от ключей, я скажу особо). Давайте добавим к ним еще один параметр в пару — y, и назовем его приоритетом. Теперь построим такое волшебное дерево, которое хранит в каждой вершине по два параметра, и при этом по ключам является деревом поиска, а по приоритетам — кучей. Такое дерево и будем далее называть декартовым.

Кстати говоря: в англоязычной литературе очень популярно название treap, которое наглядно показывает суть структуры: tree + heap. В русскоязычной же иногда можно встретить составленные по такому же принципу: дерамида (дерево + пирамида) или дуча (дерево + куча).

Почему дерево называется декартовым? Это сразу станет ясно, как только мы попробуем его нарисовать. Возьмем какой-нибудь набор пар «ключ-приоритет» и расставим на координатной сетке соответствующие точки (x, y). А потом соединим соответствующие вершины линиями, образуя дерево. Таким образом, декартово дерево отлично укладывается на плоскости благодаря своим ограничениям, а два его основных параметра — ключ и приоритет — в некотором смысле, координаты. Результат построения показан на рисунке: слева в стандартной нотации дерева, справа — на декартовой плоскости.


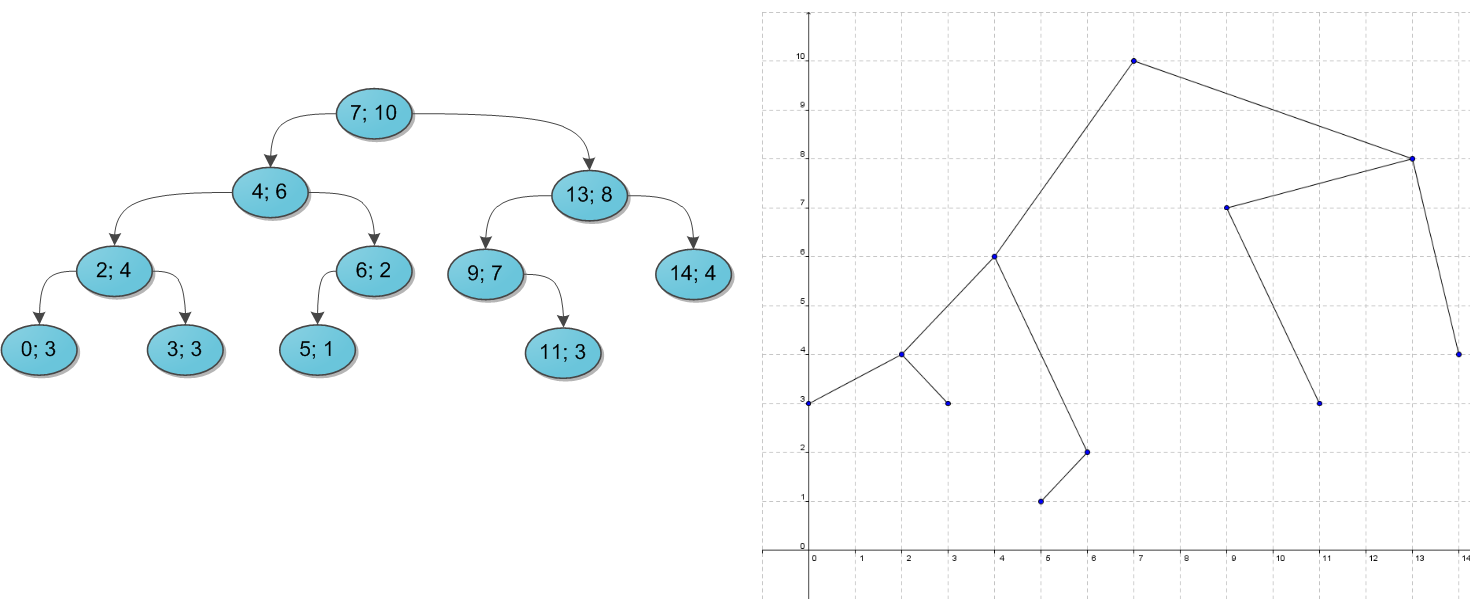
Пока что не очень понятно, зачем такое нужно. А разгадка проста, и кроется она в следующих утверждениях. Во-первых, пусть дано множество ключей: корректных деревьев поиска из них можно построить много различных, в том числе и спископодобное. А вот после добавления к ним приоритетов дерево из данных ключей можно построить уже лишь одно-единственное, вне зависимости от порядка поступления ключей. Это довольно очевидно.
А во-вторых, давайте теперь сделаем наши приоритеты случайными. То есть просто ассоциируем с каждым ключом случайное число из достаточно большого диапазона, и именно оно и будет служить соответствующим игреком. Тогда полученное декартово дерево с очень высокой, стремящейся к 100% вероятностью, будет иметь высоту, не превосходящую 4 log₂ N. (Оставлю этот факт здесь без доказательства.) А значит, хоть оно может и не быть идеально сбалансированным, время поиска ключа в таком дереве все равно будет порядка O(log₂ N), чего мы, собственно, и добивались.

Еще один интересный подход — не делать приоритеты случайными, а вспомнить о том, что у нас есть огромное количество какой-то дополнительной пользовательской информации, которую, как правило, приходится хранить в вершинах дерева. Если есть основания считать, что эта информация по сути своей достаточно случайна (день рождения пользователя, к примеру), то можно попробовать ее использовать в корыстных целях. Взять в качестве приоритета либо непосредственно информацию, либо результат какой-то функции от нее (только тогда функция должна быть обратима, чтобы восстанавливать при необходимости информацию из приоритетов). Впрочем, тут действовать приходится на свой страх и риск — если дерево через какое-то время сильно разбалансируется и вся программа начнет ощутимо тормозить, придется срочно мудрить что-нибудь во спасение ситуации.

Далее для простоты изложения предположим, что все ключи и все приоритеты в деревьях различны. На самом деле возможность равенства ключей не создает никаких особых проблем, вам просто нужно четко определиться, где будут находиться элементы, равные данному x — либо только в левом его поддереве, либо только в правом. Равенство приоритетов по идее тоже не составляет особой проблемы, кроме загрязнения доказательств и рассуждений особыми случаями, но на практике лучше его избегать. Случайная генерация целых приоритетов вполне подходит в большинстве случаев, вещественных между 0 и 1 — почти во всех случаях.

Перед началом рассказа об операциях приведу заготовку класса C#, который будет реализовывать наше декартово дерево.

public class Treap
{
    public int x;
    public int y;

    public Treap Left;
    public Treap Right;    

    private Treap(int x, int y, Treap left = null, Treap right = null)
    {
        this.x = x;
        this.y = y;
        this.Left = left;
        this.Right = right;
    }
    
    // здесь будут операции...
}

Я сделал для простоты изложения x и y типа int, но понятно, что на их месте мог бы быть любой тип, экземпляры которого мы умеем сравнивать между собой — то есть любой, реализующий IComparable или IComparable<T> в терминах C#. В Haskell это мог бы быть любой тип из класса Ord, в F# — любой с ограничениями на оператор сравнения, в Java — реализующий интерфейс Comparable<T1>, и так далее.

Магия клея и ножниц

На повестке дня насущные вопросы — как работать с декартовым деревом. Вопрос о том, как же его вообще строить из сырого набора ключей, я немного отложу, а пока что предположим, что какая-то добрая душа начальное дерево нам уже построила, и теперь нам требуется его по необходимости менять.

Вся подноготная работы с декартовым деревом заключается в двух основных операциях: Merge и Split. С помощью них элементарно выражаются все остальные популярные операции, так что начнем с основ.

Операция Merge принимает на вход два декартовых дерева L и R. От нее требуется слить их в одно, тоже корректное, декартово дерево T. Следует заметить, что работать операция Merge может не с любыми парами деревьев, а только с теми, у которых все ключи одного дерева ( L ) не превышают ключей второго ( R ). (Обратите особое внимание на это условие — оно нам еще не раз пригодится в будущем!)


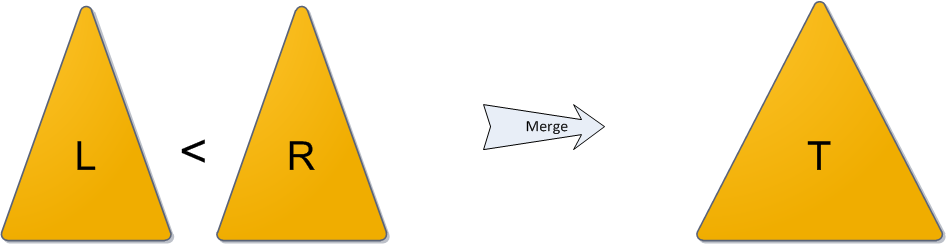
Алгоритм работы Merge очень прост. Какой элемент станет корнем будущего дерева? Очевидно, с наибольшим приоритетом. Кандидатов на максимальный приоритет у нас два — только корни двух исходных деревьев. Сравним их приоритеты; пускай для однозначности приоритет y левого корня больше, а ключ в нем равен x. Новый корень определен, теперь стоит подумать, какие же элементы окажутся в его правом поддереве, а какие — в левом.

Легко понять, что все дерево R окажется в правом поддереве нового корня, ведь ключи-то у него больше x по условию. Точно так же левое поддерево старого корня L.Left имеет все ключи, меньшие x, и должно остаться левым поддеревом, а правое поддерево L.Right… а вот правое должно по тем же соображениям оказаться справа, однако неясно, куда тогда ставить его элементы, а куда элементы дерева R?

Стоп, почему неясно? У нас есть два дерева, ключи в одном меньше ключей в другом, и нам нужно их как-то объединить и полученный результат привесить к новому корню как правое поддерево. Просто рекурсивно вызываем Merge для L.Right и дерева R, и возвращенное ею дерево используем как новое правое поддерево. Результат налицо.

На рисунке синим цветом показано правое поддерево результирующего дерева после операции Merge и связь от нового корня к этому поддереву.

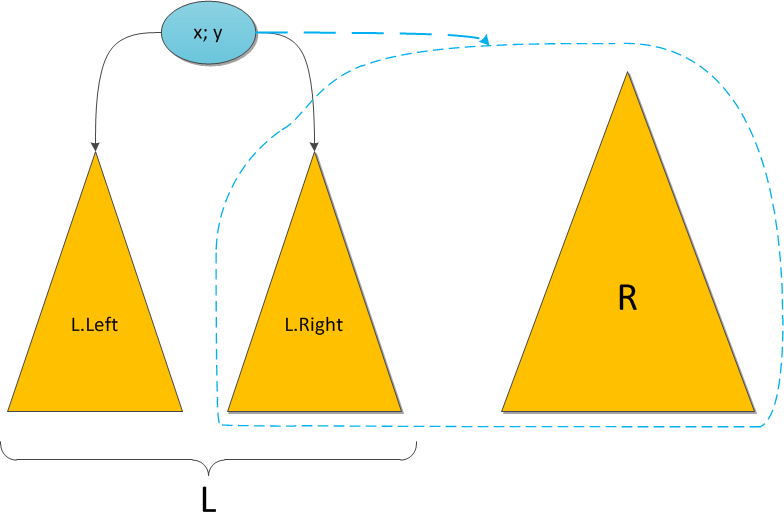
Симметричный случай — когда приоритет в корне дерева R выше — разбирается аналогично. И, конечно, надо не забыть про основу рекурсии, которая в нашем случае наступает, если какое-то из деревьев L и R, или сразу оба, являются пустыми.

Исходный код Merge:

public static Treap Merge(Treap L, Treap R)
{
    if (L == null) return R;
    if (R == null) return L;

    if (L.y > R.y)
    {
        var newR = Merge(L.Right, R);
        return new Treap(L.x, L.y, L.Left, newR);
    }
    else
    {
        var newL = Merge(L, R.Left);
        return new Treap(R.x, R.y, newL, R.Right);
    }
}

Теперь об операции Split. На вход ей поступает корректное декартово дерево T и некий ключ x₀. Задача операции — разделить дерево на два так, чтобы в одном из них ( L ) оказались все элементы исходного дерева с ключами, меньшими x₀, а в другом ( R ) — с большими. Никаких особых ограничений на дерево не накладывается.


Рассуждаем похожим образом. Где окажется корень дерева T? Если его ключ меньше x₀, то в L, иначе в R. Опять-таки, предположим для однозначности, что ключ корня оказался меньше x₀.

Тогда можно сразу сказать, что все элементы левого поддерева T также окажутся в L — их ключи ведь тоже все будут меньше x₀. Более того, корень T будет и корнем L, поскольку его приоритет наибольший во всем дереве. Левое поддерево корня полностью сохранится без изменений, а вот правое уменьшится — из него придется убрать элементы с ключами, большими x₀, и вынести в дерево R. А остаток ключей сохранить как новое правое поддерево L. Снова видим идентичную задачу, снова напрашивается рекурсия!

Возьмем правое поддерево и рекурсивно разрежем его по тому же ключу x₀ на два дерева L' и R'. После чего становится ясно, что L' станет новым правым поддеревом дерева L, а R' и есть непосредственно дерево R — оно состоит из тех и только тех элементов, которые больше x₀.

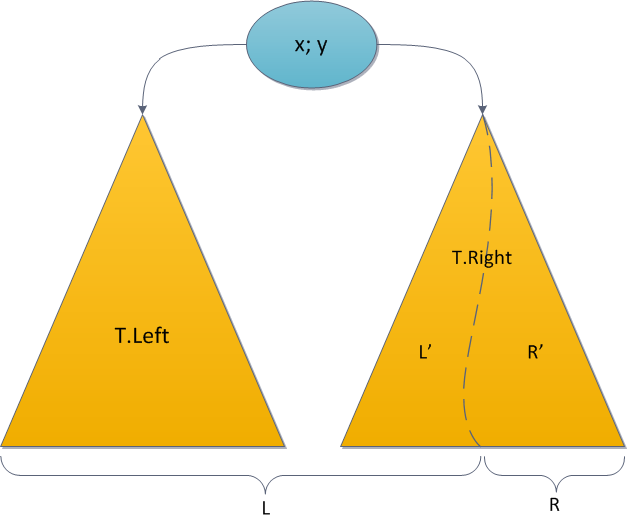
Симметричный случай, при котором ключ корня больше, чем x₀, тоже совершенно идентичен. Основа рекурсии здесь — случаи, когда какое-то из поддеревьев пустое. Ну и исходный код функции:

public void Split(int x, out Treap L, out Treap R)
{
    Treap newTree = null;
    if (this.x <= x)
    {
        if (Right == null)
            R = null;
        else
            Right.Split(x, out newTree, out R);
        L = new Treap(this.x, y, Left, newTree);
    }
    else
    {
        if (Left == null)
            L = null;
        else
            Left.Split(x, out L, out newTree);
        R = new Treap(this.x, y, newTree, Right);
    }
}

Кстати, обратите внимание: деревья, выдаваемые на выход операцией Split, подходят как входные данные для операции Merge: все ключи левого дерева не превосходят ключей в правом. Это ценное обстоятельство пригодится нам уже через несколько абзацев.

Последний вопрос — это время работы Merge и Split. Из описания алгоритма видно, что Merge за каждую итерацию рекурсии уменьшает суммарную высоту двух сливаемых деревьев как минимум на единицу, так что общее время работы не превосходит 2H, то есть O(H). А со Split все совсем просто — мы работаем с единственным деревом, его высота уменьшается с каждой итерацией тоже как минимум на единицу, и ассимптотика работы операции тоже O(H). А поскольку декартово дерево со случайными приоритетами, как уже говорилось, с высокой вероятностью имеет близкую к логарифмической высоту, то Merge и Split работают за желаемый O(log₂ N), и это дает нам потрясающий простор для их применения.

Операции с деревом

Теперь, когда мы с вами в совершенстве владеем клеем и ножницами, не составляет совершенно никакого труда только с помощью них реализовать самые необходимые действия с декартовым деревом: добавление элемента в дерево и удаление его. Я приведу самый простой вариант их реализации, основанный целиком на Merge и Split. Он будет работать за все то же логарифмическое время, однако отличаться, как говорят ACM-олимпийцы, большей константой: то есть порядок зависимости времени работы от размера дерева будет все так же O(log₂ N), но точное время работы отличаться в несколько раз — в константу раз. Скажем, 4 log₂ N против просто log₂ N. На практике это различие почти не ощущается, пока размер дерева не достигнет поистине галактических размеров.

Существуют и оптимальные реализации как добавления с удалением, так и прочих нужных операций дерамиды, константа у которых значительно меньше. Я обязательно приведу эти реализации в одной из следующих частей цикла, а также поговорю о подводных камнях, связанных с использованием более быстрого варианта. Подводные камни в первую очередь связаны с необходимостью поддержки дополнительных запросов к дереву и хранению в нем особой информации… впрочем, не буду сейчас забивать этим голову читателю, до множественных операций с деревом (чрезвычайно важной фичи!) время еще дойдет.

Итак, пускай нам дано декартово дерево и некий элемент x, который требуется в него вставить (как мы помним, в контексте статьи предполагается, что все элементы различны и икса в дереве еще нет). Хочется применить подход из двоичного дерева поиска: идти вниз по ключам, выбирая каждый раз путь влево или вправо, пока не найдем место, куда можно вставить наш x, и дописать его. Но это решение неправильное, ведь мы забыли о приоритетах. Место, куда алгоритм дерева поиска захочет добавить новую вершину, однозначно удовлетворяет ограничениям дерева поиска по x, однако может нарушить ограничение кучи по y. Значит, придется действовать немного выше и абстрактней.

Второй вариант решения — представить новый ключ как дерево из единственной вершины (со случайным приоритетом y), и слить его с исходным с помощью Merge. Это опять неверно: в исходном дереве могут быть вершины с ключами, большими x, и тогда мы нарушаем обещание, данное функции Merge касательно взаимоотношения между ее входными деревьями.

Проблему можно исправить. Помня универсальность операций Split/Merge, решение напрашивается практически сразу:

1. Разделим (split) дерево по ключу x на дерево L, с ключами меньше икса, и дерево R, с большими.
2. Создадим из данного ключа дерево M из единственной вершины (x, y), где y — только что сгенерированный случайный приоритет.
3. Объединим (merge) по очереди L с M, то что получилось — с R.

Все шаги алгоритма можно и проиллюстрировать.

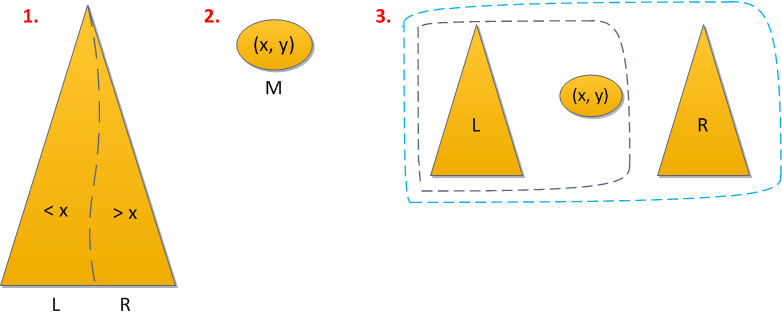
У нас тут 1 применение Split, и 2 применения Merge — общее время работы O(log₂ N). Короткий исходный код прилагается.

public Treap Add(int x)
{
    Treap l, r;
    Split(x, out l, out r);
    Treap m = new Treap(x, rand.Next());
    return Merge(Merge(l, m), r);
}

С удалением тоже не возникает никаких вопросов. Пускай нас просят удалить из декартова дерева элемент с ключем x. Сейчас я предполагаю, что вы разобрались с равенством ключей, отдав преимущество левой стороне: в правом поддереве вершины с ключем x другие элементы с тем же ключем не встречаются, а вот в левом могут. Тогда совершим следующую последовательность действий:

1. Разделим сначала дерево по ключу x-1. Все элементы, меньшие либо равные x-1, отправились в левый результат, значит, искомый элемент — в правом.
2. Разделим правый результат по ключу x (здесь стоит быть аккуратным с равенством!). В новый правый результат отправились все элементы с ключами, большими x, а в «средний» (левый от правого) — все меньшие либо равные x. Но поскольку строго меньшие после первого шага все были отсеяны, то среднее дерево и есть искомый элемент.
3. Теперь просто объединим снова левое дерево с правым, без среднего, и дерамида осталась без ключей x.

Теперь понятно, почему я постоянно акцентировал внимание на том, как же все-таки необходимо учитывать равенство ключей. Скажем, если бы ваш компаратор считал, что элементы с равными ключами надо отправлять в правое поддерево, то на первом шаге вам пришлось бы делить по ключу x, а на втором — по x+1. А вот если бы конкретики в этом вопросе вообще не было, то процедура удаления в данном варианте вообще могла бы и не выполнить желаемое — после второго шага в качестве среднего дерева останется пустое, а искомый элемент куда-то ускользнул, либо влево, либо вправо, и ищи его теперь.

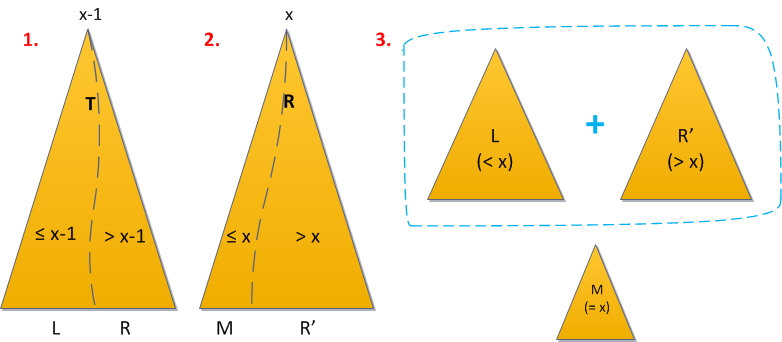
Время работы операции все так же O(log₂ N), поскольку мы применили 2 раза Split и 1 раз Merge.
Исходный код:

public Treap Remove(int x)
{
    Treap l, m, r;
    Split(x - 1, out l, out r);
    r.Split(x, out m, out r);
    return Merge(l, r);
}

Акт творения

Теперь, зная алгоритм добавления элемента в готовое декартово дерево, мы можем привести простейший способ построить дерево из поступающего набора ключей: просто добавлять их по очереди стандартным алгоритмом, начав с дерева из одной вершины — первого ключа. Помня, что операция добавления выполняется за логарифмическое время, мы получим общее время выполнения полного построения дерева — O(N log₂ N).

Интересно, а быстрее можно?

Как оказалось, в некоторых случаях — да. Давайте представим, что ключи нам на вход поступают в возрастающем порядке. Такое в принципе вполне может произойти, если это какие-то свежесоздающиеся идентификаторы с auto increment. Так вот, в таком случае существует несложный алгоритм построения дерева за O(N). Правда, нам придется заплатить за это временным overhead`ом по памяти: хранить для каждой вершины строящегося дерева ссылку на ее предка (на самом деле даже не обязательно для каждой, но это уже тонкости).

Будем хранить ссылку на последнюю добавленную вершину в дереве. По совместимости она будет в нем самой правой — ведь ключ у нее наибольший из всех ключей дерева, построенного на данный момент. Теперь допустим, что на вход поступает следующий ключ x с каким-то приоритетом y. Куда его поместить?

Последняя вершина суть самая правая, следовательно, правого сына у нее нет. Если ее приоритет больше, чем y добавляемой, то можно просто приписать новую вершину правым сыном и с чистой совестью переходить к следующему ключу на входе. В противном же случае надо подумать. У новой вершины все равно наибольший ключ, так что в конечном итоге она точно станет самой правой вершиной дерева. Стало быть, искать место для ее вставки где-либо, кроме как по самой правой ветви, смысла не имеет. Найти же нам нужно всего лишь место, где приоритет вершины больше, чем y. Итак, поднимемся от самой правой вверх по ветви, каждый раз проверяя приоритет текущей осматриваемой вершины. В конце концов мы либо придем в корень, либо остановимся где-то посреди ветви.

Предположим, мы пришли в корень. Тогда оказывается, что y больше, чем все приоритеты в дереве. У нас не остается другого выбора, кроме как сделать (x, y) новым корнем и привесить к ней старое дерево левым сыном.

Если же в корень мы не пришли — ситуация похожая. В некоторой вершине правой ветви (x₀, y₀) имеем y₀ > y. А у ее непосредственного правого потомка приоритет меньше y. Чтобы сохранить структуру дерева поиска по ключам, и сделать (x, y) самой правой в дереве, мы подвешиваем её как нового правого сына к (x₀, y₀), а все старое правое поддерево становится левым поддеревом (x, y).

Чтобы было понятнее, я проиллюстрирую на примерах. Возьмем некоторое декартово дерево и покажем, что произойдет, если в него пытаться добавлять те или иные вершины. Ключ везде тот же (22), а приоритет поварьируем.
y = 4:

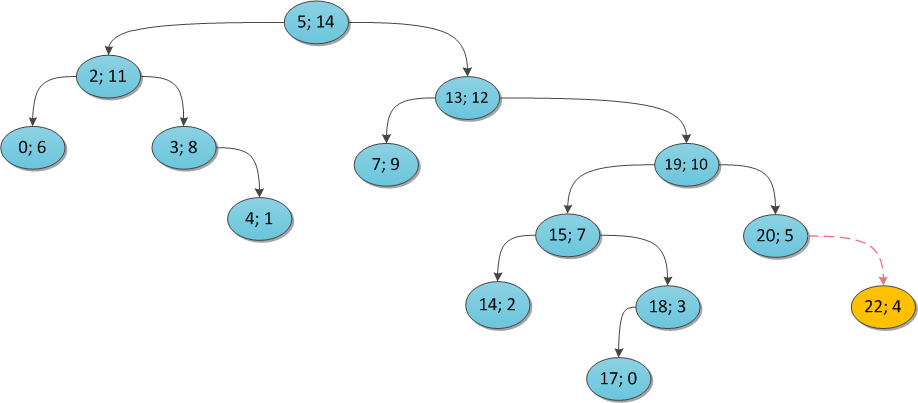
y = 16:

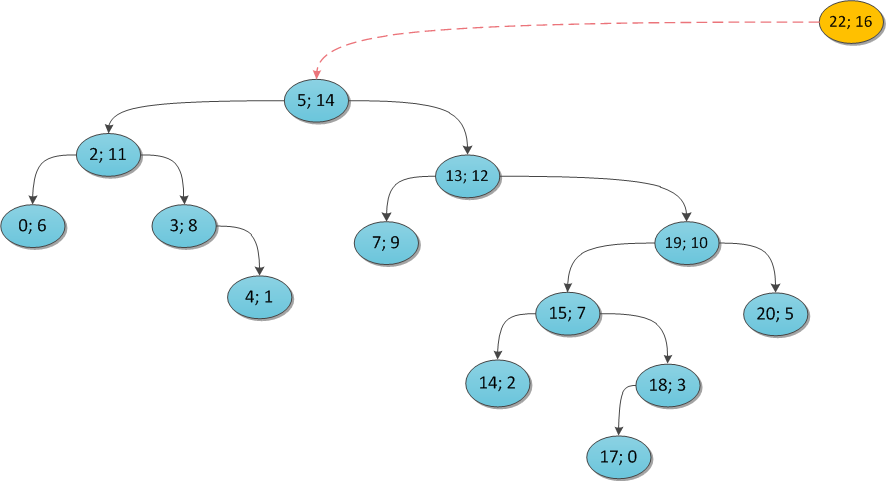
y = 11:


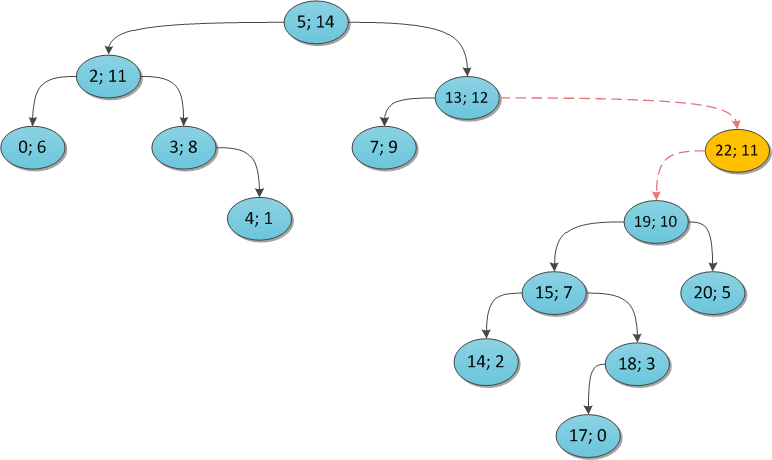
Почему этот алгоритм работает за O(N)? Заметьте, что каждую вершину дерева вы в ее жизни посетите максимум два раза:

• при ее непосредственном добавлении;
• возможно, при добавлении какой-то другой, пока она будет оставаться в правой ветви. Сразу после этого из правой ветви она уйдет и более посещаться не будет.

Таким образом, общее количество переходов не превосходит 2N, и ассимптотика построения — O(N).

На закуску — исходный код построения по заданному массиву ключей и приоритетов. Здесь предполагается, что у каждой вершины дерева есть еще свойство Parent, а также что опциональный параметр с таким же именем есть у уже использовавшегося приватного конструктора вершины (пятый по счету).

public static Treap Build(int[] xs, int[] ys)
{
    Debug.Assert(xs.Length == ys.Length);

    var tree = new Treap(xs[0], ys[0]);
    var last = tree;

    for (int i = 1; i < xs.Length; ++i)
    {
        if (last.y > ys[i])
        {
            last.Right = new Treap(xs[i], ys[i], parent: last);
            last = last.Right;
        }
        else
        {
            Treap cur = last;
            while (cur.Parent != null && cur.y <= ys[i])
                cur = cur.Parent;
            if (cur.y <= ys[i])
                last = new Treap(xs[i], ys[i], cur);
            else
            {
                last = new Treap(xs[i], ys[i], cur.Right, null, cur);
                cur.Right = last;
            }
        }
    }

    while (last.Parent != null)
        last = last.Parent;
    return last;
}

Резюме

Мы с вами построили древовидную структуру данных с такими свойствами:

• обладает почти гарантированно логарифмической высотой относительно количества своих вершин;
• позволяет за логарифмическое время искать любой ключ в дереве, добавлять его и удалять;
• исходный код всех её методов не превышает 20 строк, они легко понимаются и в них крайне сложно ошибиться
• содержит некоторый overhead по памяти, сравнительно с истинно самобалансирующимися деревьями, на хранение приоритетов.

В принципе, результат довольно-таки мощный. Однако некоторым может быть все же неясно, стоило ли ради него городить настолько большой огород с такой кучей текста. Стоило. Фишка в том, что возможности декартового дерева и потенциал его применения далеко не ограничиваются функциями, описанными в этой статье. Это лишь предисловие.

В следующих частях:

1. Множественные операции над декартовым деревом (ищем за O(log₂ N) сумму, максимум и т.д.)
2. Декартово дерево по неявному ключу (или как усовершенствовать обычный массив)
3. Ускоренные реализации функций декартового дерева (и их проблемы)
4. Функциональная реализация декартового дерева на F#.

Источники

Источники указываю раз и навсегда, они одни и те же для всех планируемых статей.

В первую очередь при написании этих статей я основываюсь на лекции Виталия Гольдштейна, рассказанной на Харьковской зимней школе по программированию ACM ICPC в 2010 году. Ее можно загрузить из видеогалереи школы (год 2010, день 2), как только она снова заработает, потому что в последние дни сервер что-то катастрофически барахлит.

Сайт Максима «e-maxx» Иванова — богатый кладезь информации по разным алгоритмам и структурам данных, использующихся в спортивном программировании. В частности, есть на нем и статья про декартово дерево.

В знаменитой книге Кормен, Лейзерсон, Ривест, Штайн «Алгоритмы: построение и анализ» можно найти доказательство того, что матожидание высоты случайного двоичного дерева поиска есть O(log₂ N), хотя его определение случайного дерева поиска и отличается от того, что мы здесь использовали.

Впервые дерамиды были предложены в статье Seidel, Raimund; Aragon, Cecilia R. (1996), «Randomized Search Trees». В принципе там можно найти полный объем информации по теме.

Пока что все. Надеюсь, вам было интересно :)