Доброго времени суток, хабравчане! В этой статье я подробно расскажу вам о трансформации и вращении в javascripte. Матрица трансформаций, на первый взгляд, штука непонятная и многие ею пользуются даже не осознавая, что она делает на самом деле, используя готовые значения из интернета. На MDC об этом рассказано скудненько, а информацию в английской Википедии тяжело назвать общедоступной. Постараемся разобраться в этом вместе.Translate
Translate — самый лёгкий метод из трансформирующих. Он всего лишь сдвигает все адресованные пиксели на указанные значения:
ctx.translate(x,y). Нюансы работы с ним мы рассмотрим подробнее ниже.Экспериментируем с translate
Scale
Scale, как и translate, принимает в качестве аргументов x и y — значения, на которые надо умножить соответствующую ось. К примеру, при ctx.scale(2,3) всё будет отрисовываться в два раза шире и в три раза выше. Указав X=-1 мы отзеркалим изображение налево, указав y=-1 мы отзеркалим изображение вверх.
Экспериментируем со scale
Rotate
Rotate принимает в качестве параметра угол в радианах, на который надо повернуть изображение вокруг точки опори (pivot), заданной методом translate (по-умолчанию 0:0). Перевести градусы в радианы можно с помощью простой формулы, которая является основой метода Number.degree в LibCanvas:
Number.prototype.degree = function () {
return this * Math.PI / 180;
};
(60).degree() // 60 градусов в радианах
Экспериментируем с rotate
Если мы хотим вращать какой-то объект, например, картинку, необходимо правильно взаимодействовать методами rotate и translate, иначе мы никогда не попадём картинкой в нужное место. Самый простой способ осью вращения выбрать центр картинки и отрисовывать её в координаты (-width/2, -height/2). К примеру, мы хотим развернуть картинку размерами 50х50, находящуюся на координатах 100:100. Указываем translate в координату 125:125 и отрисовываем картинку в координату -25:-25. Альтернатива — использовать LibCanvas и метод rotatedImage(или drawImage в ближайшем будущем) и не напрягаться.
Вращаем картинку
setTransform
ctx.setTransform(m11, m12, m21, m22, dx, dy);
Рассмотрим по очереди, за что отвечает каждый из аргументов.
dx, dy — повторяют метод translate, смещая картинку на соответствующие значения.m11, m22 — повторяют метод scale, изменяя размер отрысовываемых пикселей.m12, m21 — более интересные. Каждый пиксель (x,y) смещается на y*m21 пикселей вправо и на x*m12 пикселей вниз.Это значит, что при m21=1 каждая следующая строчка будет смещена на 1 пиксель вправо, относительно предыдущей.Экспериментируем с setTransform
Метод transform действует точно также, но в отличии от setTransform не обнуляет каждый раз предыдущую трансформацию, а накладывается поверх неё. Что можно из этого получить?
Изометрическая карта
Давайте из тайловой 2D-карты с видом сверху сделаем изометрическую с помощью простой трансформации. Самый простая фигура изометрической проекции — это ромб, в котором горизонтальная диагональ в два раза больше вертикальной (он шире в два раза чем выше). Его можно сделать в три шага.
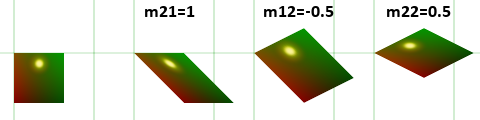
Смещаем его вправо при помощи m21=1, поднимаем вверх при помощи m12=-0.5 и сплюскиваем при помощи m22=0.5 (вы можете по шагам повторить это в песочнице).
Но это будет изометрическая проекция с углом 26,565° к горизонтали. Если мы хотим настоящую изометрическую проекцию с углом 30° — необходимо слегка сплюснуть его по ширине, изменив ширину ячейки по оси Х, что легко высчитать следующим методом:
Мы видим, что ячейка — это ромб ABCD с центром в точке O. Угол BAO — и есть угол, который надо из 26.6 сделать 30. Сейчас AO=BD, то есть высота равнобедренного трехугольника BAD равна его основе. Нам необходимо этот трехугольник сделать равносторонним (чтобы угол BAD стал равен 60 градусам), то есть уменьшить высоту на какой-то коэфициент. Допустим, AO = BD = 1 попугай. Тогда AO должна быть равна sqrt(AB2-BO2) = sqrt(1-0.25) = 0.866 попугая. Вот этот коэфициент мы и используем в нашей матрице:
ctx.setTransform(0.866, -0.5, 0.866, 0.5, 0, 0)
Смотрим, какая у нас получилась карта
Надеюсь, все понятно описала. Задавайте вопросы, предлагайте, будем вместе пополнять топик.
